Hasuer's Studio.

1. Pattern Two Pointers

Grokking Interview Pattern Interview
Word count: 10.5kReading time: 65 min
2024/05/01

Introduction

Introduction to Two Pointers Pattern

In problems where we deal with sorted arrays (or linked-lists) and need to find a set of elements that fulfill certain constraints, the Two Pointers approach becomes quite useful. The set of elements could be a pair, a triplet or even a subarray. For example, take a look at the following problem:

Given an array of sorted numbers and a target sum, find a pair in the array whose sum is equal to the given target.

To solve this problem, we can consider each element one by one (indicated by the first pointer) and iterate through the remaining elements (indicated by the second pointer) to find a pair with the given sum. The time complexity of this algorithm will be , where ‘N’ is the number of elements in the input array.

Given that the input array is sorted, an efficient approach would be to start with one pointer at the beginning and another pointer at the end. At every step, we will check if the numbers indicated by the two pointers add up to the target sum. If they do not, we have two options:

  1. If the sum of the two numbers indicated by the two pointers is greater than the target sum, this means that we need a pair with a smaller sum. To explore more pairs, we can decrement the end-pointer.
  2. If the sum of the two numbers indicated by the two pointers is smaller than the target sum, this means that we need a pair with a larger sum. To explore more pairs, we can increment the start-pointer.

Here is the visual representation of this algorithm:

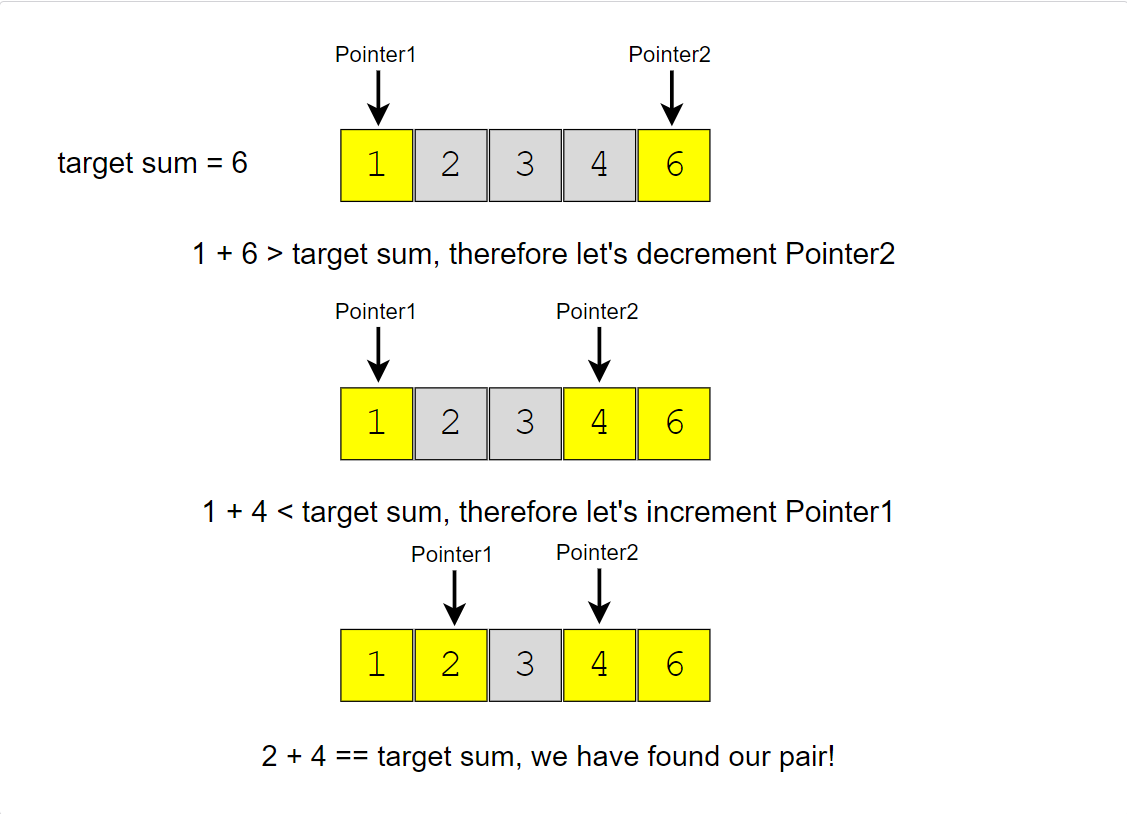
The time complexity of the above algorithm will be O(N).

In the following chapters, we will apply the Two Pointers approach to solve a few problems.

Pair with Target Sum (easy)

Similar | Top Interview 150 | 1. Two Sum Design Gurus Educative.io

Problem Statement

Given an array of numbers sorted in ascending order and a target sum, find a pair in the array whose sum is equal to the given target. If no such pair exists return [-1, -1].

Write a function to return the indices of the two numbers (i.e. the pair) such that they add up to the given target.

Example 1:

1
2
3
Input: [1, 2, 3, 4, 6], target=6
Output: [1, 3]
Explanation: The numbers at index 1 and 3 add up to 6: 2+4=6

Example 2:

1
2
3
Input: [2, 5, 9, 11], target=11
Output: [0, 2]
Explanation: The numbers at index 0 and 2 add up to 11: 2+9=11

Constraints:

  • 2 <= arr.length <= 10^4
  • -109 <= arr[i] <= 10^9
  • -109 <= target <= 10^9

Solution

Since the given array is sorted, a brute-force solution could be to iterate through the array, taking one number at a time and searching for the second number through Binary Search. The time complexity of this algorithm will be O(N\logN)*. Can we do better than this?

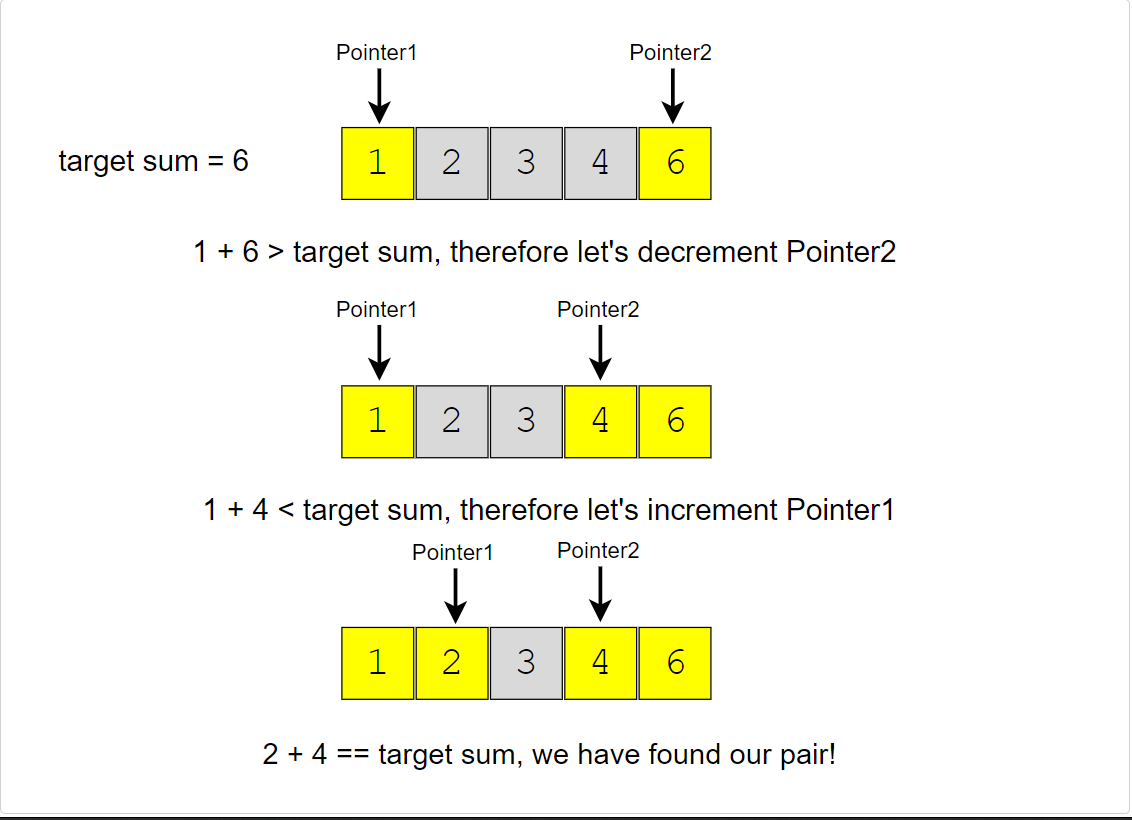
We can follow the Two Pointers approach. We will start with one pointer pointing to the beginning of the array and another pointing at the end. At every step, we will see if the numbers pointed by the two pointers add up to the target sum. If they do, we have found our pair; otherwise, we will do one of two things:

  1. If the sum of the two numbers pointed by the two pointers is greater than the target sum, this means that we need a pair with a smaller sum. So, to try more pairs, we can decrement the end-pointer.
  2. If the sum of the two numbers pointed by the two pointers is smaller than the target sum, this means that we need a pair with a larger sum. So, to try more pairs, we can increment the start-pointer.

Here is the visual representation of this algorithm for Example-1:

Code

Here is what our algorithm will look like:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution:
  def search(self, arr, target_sum):
    left, right = 0, len(arr) - 1
    while(left < right):
      current_sum = arr[left] + arr[right]
      if current_sum == target_sum:
        return [left, right]

      if target_sum > current_sum:
        left += 1  # we need a pair with a bigger sum
      else:
        right -= 1  # we need a pair with a smaller sum
    return [-1, -1]

def main():
  sol = Solution();
  print(sol.search([1, 2, 3, 4, 6], 6))
  print(sol.search([2, 5, 9, 11], 11))


main()

Time Complexity

  1. Initialization: Constant time, O(1), as it involves assigning values to left and right.

  2. While Loop:

    • The while loop runs as long as left is less than right.
    • In the worst case, this loop iterates over all elements of the array once. This happens when no pair is found, or the pair is found at the extreme ends of the array.
    • Each iteration involves a constant amount of work: calculating currentSum, comparing it with targetSum, and then incrementing left or decrementing right.

    Therefore, the loop runs in O(n) time, where is the number of elements in the array.

  3. Overall: The dominant factor in this algorithm is the while loop, making the overall time complexity O(n).

Space Complexity

  • The algorithm uses a fixed amount of extra space: variables left, right, and currentSum.
  • It does not depend on the size of the input array, as no additional data structures are used that grow with the input size.
  • Thus, the space complexity is O(1), constant space.

In summary, the algorithm has a time complexity of O(n)and a space complexity of O(1).

An Alternate approach

Similar | Top Interview 150 | 1. Two Sum

Instead of using a two-pointer or a binary search approach, we can utilize a HashTable to search for the required pair. We can iterate through the array one number at a time. Let’s say during our iteration we are at number ‘X’, so we need to find ‘Y’ such that “X + Y == Target”. We will do two things here:

  1. Search for ‘Y’ (which is equivalent to “Target - X“ in the HashTable. If it is there, we have found the required pair.
  2. Otherwise, insert “X” in the HashTable, so that we can search it for the later numbers.

Here is what our algorithm will look like:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution:
  def pair_with_targetsum(self, arr, target_sum):
    nums = {}  # to store numbers and their indices
    for i, num in enumerate(arr):
      if target_sum - num in nums:
       return [nums[target_sum - num], i]
      else:
       nums[num] = i
    return [-1, -1]


def main():
  sol = Solution()
  print(sol.pair_with_targetsum([1, 2, 3, 4, 6], 6))
  print(sol.pair_with_targetsum([2, 5, 9, 11], 11))


main()

Time Complexity

  1. HashMap Initialization: Constant time, (O(1)).

  2. For Loop:

    • The for loop iterates over each element of the array once.
    • In each iteration, the algorithm checks if the element is already present in the HashMap (or dictionary in Python) and either returns a result or inserts an element into the HashMap.
    • This element checking or insertion operations of a HashMap generally operate in (O(1)) time due to efficient hashing. However, in the worst case (e.g., when many hash collisions occur), these operations can degrade to (O(n)). Under the assumption of a good hash function with minimal collisions, these operations can be considered (O(1)).

    Therefore, the loop runs in (O(n)) time in the average case, where (n) is the number of elements in the array.

  3. Overall: The dominating factor in this algorithm is the for loop. Under the assumption of efficient hashing, the overall average time complexity is (O(n)).

Space Complexity

  • The algorithm uses a HashMap to store elements from the array. In the worst case, this map can store all elements of the array if no pair is found that adds up to the target sum
  • Thus, the space complexity is proportional to the number of elements in the array, which is (O(n)).

In summary, the algorithm has an average time complexity of (O(n)) and a space complexity of (O(n)). The time complexity can degrade to (O(n^2)) in the worst case due to potential hash collisions, but this is generally not the common case with a good hash function.

Remove Duplicates (easy)

Top Interview 150 | 26. Remove Duplicates from Sorted Array Similar | Top Interview 150 | 80. Remove Duplicates from Sorted Array II Similar | 83. Remove Duplicates from Sorted List Similar | Top Interview 150 | 82. Remove Duplicates from Sorted List II Similar | 1089. Duplicate Zeros Design Gurus Educative.io

Find Non-Duplicate Number Instances

Problem Statement

Given an array of sorted numbers, move all non-duplicate number instances at the beginning of the array in-place. The non-duplicate numbers should be sorted and you should not use any extra space so that the solution has constant space complexity i.e., .

Move all the unique number instances at the beginning of the array and after moving return the length of the subarray that has no duplicate in it.

Example 1:

1
2
3
Input: [2, 3, 3, 3, 6, 9, 9]
Output: 4
Explanation: The first four elements after moving element will be [2, 3, 6, 9].

Example 2:

1
2
3
Input: [2, 2, 2, 11]
Output: 2
Explanation: The first two elements after moving elements will be [2, 11].

Constraints:

  • 1 <= nums.length <= 3 * 10^4
  • -100 <= nums[i] <= 100
  • nums is sorted in non-decreasing order.

Solution

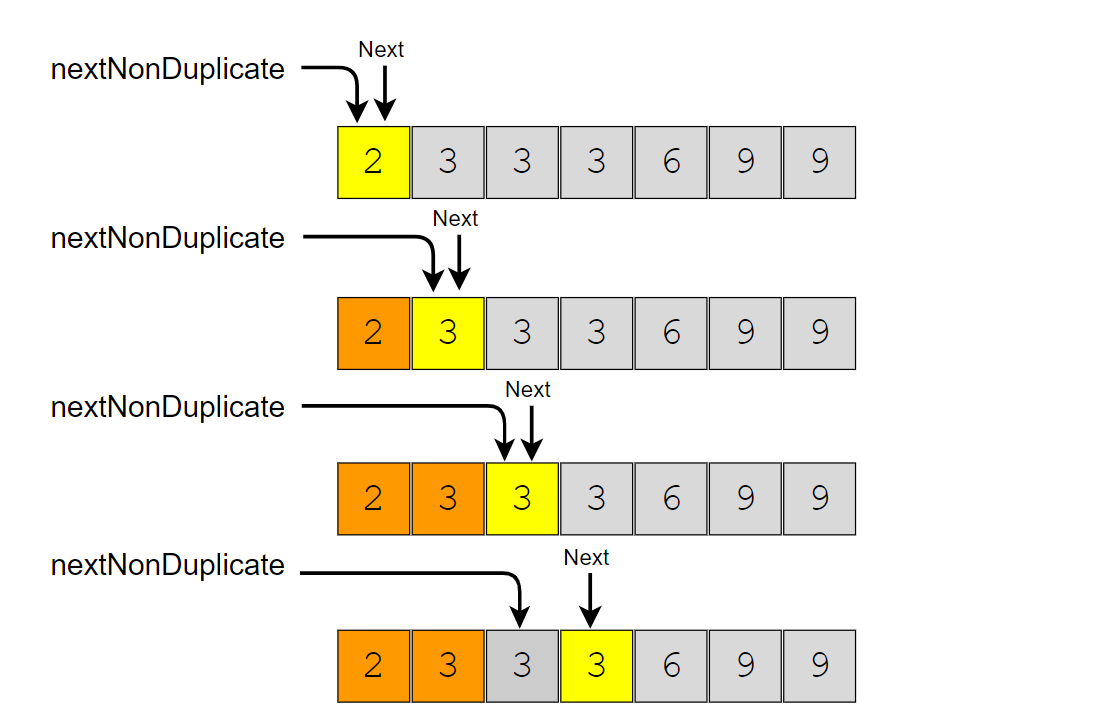
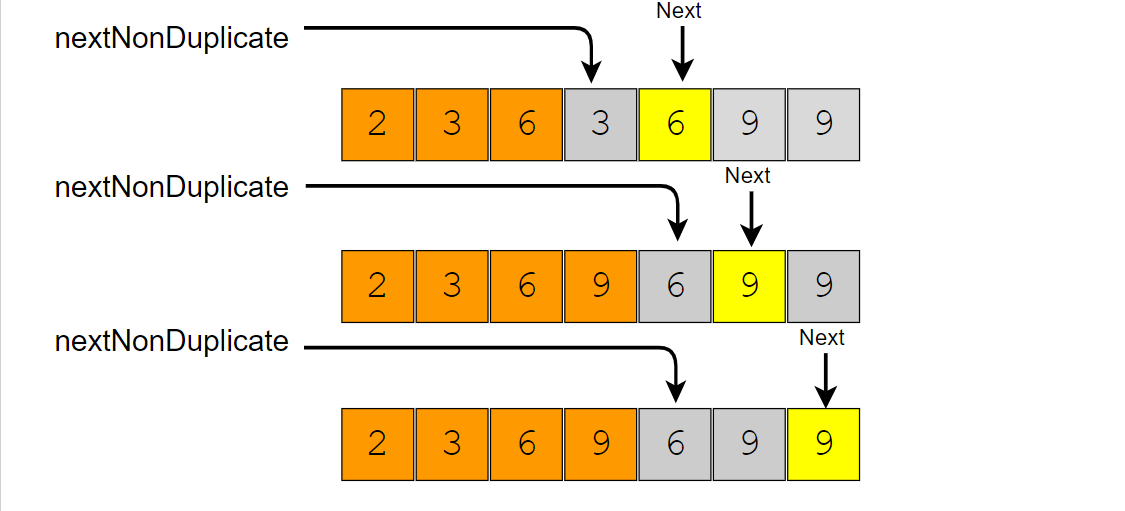
In this problem, we need to separate the duplicate elements in-place such that the resultant length of the array remains sorted. As the input array is sorted, one way to do this is to shift the elements left whenever we encounter duplicates. In other words, we will keep one pointer for iterating the array and one pointer for placing the next non-duplicate number. So our algorithm will be to iterate the array and whenever we see a non-duplicate number we move it next to the last non-duplicate number we’ve seen.

Here is the visual representation of this algorithm for Example-1:

Code

Here is what our algorithm will look like:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
class Solution:
  def moveElements(self, arr):
    # Initialize the index for the next non-duplicate element
    next_non_duplicate = 1

    # Initialize the main loop index
    i = 0

    # Iterate through the array
    while i < len(arr):
      # Check if the current element is different from the previous element
      if arr[next_non_duplicate - 1] != arr[i]:
        # If different, update the next_non_duplicate element and copy the current element
        arr[next_non_duplicate] = arr[i]

        # Increment the next_non_duplicate index
        next_non_duplicate += 1

      # Increment the main loop index
      i += 1

    # Return the length of the modified array as the result
    return next_non_duplicate

# Entry point of the program
def main():
  # Create an instance of the Solution class
  sol = Solution()

  # Test the 'moveElements' method with example arrays
  print(sol.moveElements([2, 3, 3, 3, 6, 9, 9]))  # Output: 4 (modified array: [2, 3, 6, 9, 6, 9, 9])
  print(sol.moveElements([2, 2, 2, 11]))         # Output: 2 (modified array: [2, 11, 2, 11])

# Execute the main function
main()

Time Complexity

The time complexity of the above algorithm will be O(N), where ‘N’ is the total number of elements in the given array.

Space Complexity

The algorithm runs in constant space O(1).

Similar Questions

Top Interview 150 |27. Remove Element

Problem 1: Given an unsorted array of numbers and a target ‘key’, remove all instances of ‘key’ in-place and return the new length of the array.

Example 1:

1
2
3
Input: [3, 2, 3, 6, 3, 10, 9, 3], Key=3
Output: 4
Explanation: The first four elements after removing every 'Key' will be [2, 6, 10, 9].

Example 2:

1
2
3
Input: [2, 11, 2, 2, 1], Key=2
Output: 2
Explanation: The first two elements after removing every 'Key' will be [11, 1].

Solution: This problem is quite similar to our parent problem. We can follow a two-pointer approach and shift numbers left upon encountering the ‘key’. Here is what the code will look like:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution:
  def remove(self, arr, key):
    nextElement = 0  # Initialize a variable to keep track of the next non-'key' element index.
    
    # Iterate through the input array 'arr'.
    for i in range(len(arr)):
      if arr[i] != key:  # Check if the current element is not equal to 'key'.
        arr[nextElement] = arr[i]  # If not equal, copy the current element to the next available position.
        nextElement += 1  # Increment the nextElement index to prepare for the next non-'key' element.

    return nextElement  # Return the length of the modified array, which represents the new length.


def main():
  sol = Solution()
  
  # Test case 1
  print("Array new length: " + str(sol.remove([3, 2, 3, 6, 3, 10, 9, 3], 3)))
  
  # Test case 2
  print("Array new length: " + str(sol.remove([2, 11, 2, 2, 1], 2)))

main()

Time and Space Complexity: The time complexity of the above algorithm will be O(N), where ‘N’ is the total number of elements in the given array.

The algorithm runs in constant space O(1).

Squaring a Sorted Array (easy)

977. Squares of a Sorted Array Design Gurus Educative.io

Problem Statement

Given a sorted array, create a new array containing squares of all the number of the input array in the sorted order.

Example 1:

1
2
Input: [-2, -1, 0, 2, 3]
Output: [0, 1, 4, 4, 9]

Example 2:

1
2
Input: [-3, -1, 0, 1, 2]
Output: [0 1 1 4 9]

Constraints:

  • 1 <= arr.length <= 10^4
  • -104 <= arr[i] <= 10^4
  • arr is sorted in non-decreasing order.

Solution

We can use a brute-force approach to iterate the input array and calculate the square of each number. We can store these squares in a new array and then sort the resulting array using any sorting algorithm like Quicksort or Mergesort. Because of the sorting, this approach has a time complexity of O(N \ logN)*, where N is the length of the input array. Here is a Python solution for this approach:

1
2
def sorted_squares(nums):
  return sorted([num**2 for num in nums])

Can we do better than this? Can we avoid sorting? Is it possible to generate the output in sorted order?

The tricky part is that we can have negative numbers in the input array, which makes it harder to generate the output array with squares in sorted order.

One easier approach could be to first locate the index of the first positive number in the input array. After that, we can utilize the Two Pointers technique to iterate over the array, with one pointer moving forward to scan positive numbers, and the other pointer moving backward to scan negative numbers. At each step, we can compare the squares of the numbers pointed by both pointers and append the smaller square to the output array.

For the above-mentioned Example-1, we will do something like this:

Since the numbers at both ends can give us the largest square, an alternate approach could be to use two pointers starting at both ends of the input array. At any step, whichever pointer gives us the bigger square, we add it to the result array and move to the next/previous number. Please note that we will be appending the bigger square (as opposed to the previous approach) because the two pointers are moving from larger squares to smaller squares. For that, we will be inserting the squares at the end of the output array.

For the above-mentioned Example-1, we will do something like this:

Here’s a detailed walkthrough of the algorithm:

  1. We start by obtaining the length of the input array, arr, which we store in variable n. Then, we create a new array, squares, of the same length to hold the squared values. We also create a variable highestSquareIdx and set it to n - 1, the last index of squares, which will help us populate the squares array from the highest (rightmost) index towards the lowest (leftmost).
  2. We initialize two pointers, left and right, to 0 and n - 1, respectively. These pointers represent the indices of the elements at the start (lowest) and end (highest) of the array.
  3. We enter a loop that continues as long as left is less than or equal to right.
  4. In each iteration, we calculate the squares of the elements at the left and right indices, storing them in leftSquare and rightSquare respectively.
  5. We then compare leftSquare with rightSquare. The larger of these two squares is inserted at the position of highestSquareIdx in the squares array, and highestSquareIdx is decremented.
  6. If leftSquare was larger, we increment left to move towards the higher numbers in the array. If rightSquare was larger or equal, we decrement right to move towards the lower numbers in the array. We’re comparing absolute square values, so even if numbers in the array are negative, we’re dealing with their positive square.
  7. This process repeats, filling up the squares array from right to left, until left and right meet or cross each other.
  8. At this point, the squares array is filled with the squares of the numbers in the input array, sorted in ascending order. This array is then returned as the result.

Code

Here is the code for the second approach discussed above:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
class Solution:
  def makeSquares(self, arr):
    # Get the length of the input array
    n = len(arr)
    
    # Create a list to store the squares, initialized with zeros
    squares = [0 for x in range(n)]
    
    # Initialize the index for the highest square in the output array
    highestSquareIdx = n - 1
    
    # Initialize two pointers for the left and right ends of the input array
    left, right = 0, n - 1
    
    # Iterate over the input array from both ends towards the center
    while left <= right:
      # Calculate the squares of the elements at the left and right pointers
      leftSquare = arr[left] * arr[left]
      rightSquare = arr[right] * arr[right]
      
      # Compare the squares and store the larger square in the output array
      if leftSquare > rightSquare:
        squares[highestSquareIdx] = leftSquare
        left += 1
      else:
        squares[highestSquareIdx] = rightSquare
        right -= 1
      
      # Move to the next index in the output array
      highestSquareIdx -= 1

    # Return the resulting list of squares
    return squares


def main():
  sol = Solution()
  # Test the makeSquares method with example inputs
  print("Squares: " + str(sol.makeSquares([-2, -1, 0, 2, 3])))
  print("Squares: " + str(sol.makeSquares([-3, -1, 0, 1, 2])))


main()

Time complexity

The time complexity of the above algorithm will be O(N) as we are iterating the input array only once.

Space complexity

The space complexity of the above algorithm will also be O(N); this space will be used for the output array.

*Triplet Sum to Zero (medium)

Top Interview 150 | 15. 3Sum Design Gurus Educative.io

Problem Statement

Given an array of unsorted numbers, find all unique triplets in it that add up to zero.

Example 1:

1
2
3
Input: [-3, 0, 1, 2, -1, 1, -2]
Output: [[-3, 1, 2], [-2, 0, 2], [-2, 1, 1], [-1, 0, 1]]
Explanation: There are four unique triplets whose sum is equal to zero. smallest sum.'

Example 2:

1
2
3
Input: [-5, 2, -1, -2, 3]
Output: [[-5, 2, 3], [-2, -1, 3]]
Explanation: There are two unique triplets whose sum is equal to zero.

Constraints:

  • 3 <= arr.length <= 3000
  • -105 <= arr[i] <= 105

Solution

This problem follows the Two Pointers pattern and shares similarities with Pair with Target Sum. A couple of differences are that the input array is not sorted and instead of a pair we need to find triplets with a target sum of zero.

To follow a similar approach, first, we will sort the array and then iterate through it taking one number at a time. Let’s say during our iteration we are at number ‘X’, so we need to find ‘Y’ and ‘Z’ such that X + Y + Z == 0. At this stage, our problem translates into finding a pair whose sum is equal to “-X” (as from the above equation Y + Z == -X).

Another difference from Pair with Target Sum is that we need to find all the unique triplets. To handle this, we have to skip any duplicate number. Since we will be sorting the array, so all the duplicate numbers will be next to each other and are easier to skip.

Here is the detailed walk through of the algorithm:

  1. The method searchTriplets is the main method that orchestrates the process. The algorithm starts by sorting the input array.
  2. It then starts iterating over the array. For each element, it calls the method searchPair to find pairs in the rest of the array that add up to the negative value of the current element. The purpose of this is to find three numbers that add up to zero (i.e., the current number and two other numbers that add up to the negative of the current number).
  3. The searchPair method uses the two-pointer technique to find pairs that add up to a given target. It starts with one pointer at the beginning of the array (or the index after the current number) and another pointer at the end of the array. It calculates the sum of the numbers at the pointers, and if the sum is equal to the target, it adds a triplet consisting of the negative target (which is the number we’re currently processing in the searchTriplets method) and the two numbers that make up the sum to the result list.
  4. If the sum is less than the target, it means we need to increase the sum, so we move the left pointer one step to the right. If the sum is greater than the target, it means we need to decrease the sum, so we move the right pointer one step to the left.
  5. To avoid adding duplicate triplets to the list, the algorithm skips elements that are the same as the previous element both in the searchTriplets method and in the searchPair method.

In the end, the searchTriplets method returns a list of all unique triplets in the array that add up to zero.

Let’s visualize the example 2 via below diagram.

Code

Here is what our algorithm will look like:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
class Solution:
  def searchTriplets(self, arr):
    arr.sort()
    triplets = []
    for i in range(len(arr)):
      if i > 0 and arr[i] == arr[i-1]:  # skip same element to avoid duplicate triplets
        continue
      self.searchPair(arr, -arr[i], i+1, triplets)

    return triplets


  def searchPair(self, arr, target_sum, left, triplets):
    right = len(arr) - 1
    while(left < right):
      current_sum = arr[left] + arr[right]
      if current_sum == target_sum:  # found the triplet
        triplets.append([-target_sum, arr[left], arr[right]])
        left += 1
        right -= 1
        while left < right and arr[left] == arr[left - 1]:
          left += 1  # skip same element to avoid duplicate triplets
        while left < right and arr[right] == arr[right + 1]:
          right -= 1  # skip same element to avoid duplicate triplets
      elif target_sum > current_sum:
        left += 1  # we need a pair with a bigger sum
      else:
        right -= 1  # we need a pair with a smaller sum


def main():
  sol = Solution()
  print(sol.searchTriplets([-3, 0, 1, 2, -1, 1, -2]))
  print(sol.searchTriplets([-5, 2, -1, -2, 3]))


main()

Time complexity

Sorting the array will take O(N \ logN)*. The searchPair() function will take O(N). As we are calling searchPair() for every number in the input array, this means that overall searchTriplets() will take O(N \ logN + N^2)*, which is asymptotically equivalent to O(N^2).

Space complexity

Ignoring the space required for the output array, the space complexity of the above algorithm will be O(N)O(N) which is required for sorting.

Triplet Sum Close to Target (medium)

16. 3Sum Closest Design Gurus Educative.io

Problem Statement

Given an array of unsorted numbers and a target number, find a triplet in the array whose sum is as close to the target number as possible, return the sum of the triplet. If there are more than one such triplet, return the sum of the triplet with the smallest sum.

Example 1:

1
2
3
Input: [-1, 0, 2, 3], target=3 
Output: 2
Explanation: There are two triplets with distance '1' from the target: [-1, 0, 3] & [-1, 2, 3]. Between these two triplets, the correct answer will be [-1, 0, 3] as it has a sum '2' which is less than the sum of the other triplet which is '4'. This is because of the following requirement: 'If there are more than one such triplet, return the sum of the triplet with the smallest sum.'

Example 2:

1
2
3
Input: [-3, -1, 1, 2], target=1
Output: 0
Explanation: The triplet [-3, 1, 2] has the closest sum to the target.

Example 3:

1
2
3
Input: [1, 0, 1, 1], target=100
Output: 3
Explanation: The triplet [1, 1, 1] has the closest sum to the target.

Example 4:

1
2
3
Input: [0, 0, 1, 1, 2, 6], target=5
Output: 4
Explanation: There are two triplets with distance '1' from target: [1, 1, 2] & [0, 0, 6]. Between these two triplets, the correct answer will be [1, 1, 2] as it has a sum '4' which is less than the sum of the other triplet which is '6'. This is because of the following requirement: 'If there are more than one such triplet, return the sum of the triplet with the smallest sum.'

Constraints:

  • 3 <= arr.length <= 500
  • -1000 <= arr[i] <= 1000
  • -104 <= target <= 10^4

Solution

This problem follows the Two Pointers pattern and is quite similar to “Triplet Sum to Zero”.

We can follow a similar approach to iterate through the array, taking one number at a time. At every step, we will save the difference between the triplet and the target number, so that in the end, we can return the triplet with the closest sum.

Here’s a detailed walkthrough of the algorithm:

  1. Initially, the method checks whether the input array arr is null or its length is less than 3. If either condition is true, the method throws an IllegalArgumentException, as it is impossible to find a triplet in these cases.
  2. The input array arr is then sorted in ascending order. Sorting is important as it allows us to move our pointers based on the sum we are getting and how close we are to the target sum.
  3. The smallestDifference variable is initialized to Integer.MAX_VALUE, which will keep track of the smallest difference we have found so far between our target sum and the sum of our current triplet.
  4. The function then iterates through arr using a for loop, stopping when it is two positions from the end of arr (arr.length - 2). This is because we are always looking for triplets and thus don’t need to consider the last two positions in this loop.
  5. Inside the for loop, two pointers, left and right, are initialized. left is set to i + 1 (one position to the right of our current position) and right is set to the last index of the array (arr.length - 1).
  6. We start a while that continues as long as left is less than right. Inside this loop, we calculate the difference between the target sum and the sum of the numbers at our current positions in the array (targetDiff). This allows us to see how close the current triplet sum is to our target sum.
  7. If targetDiff equals 0, that means the sum of our current triplet exactly matches the target sum, and we return the targetSum immediately as our result.
  8. Otherwise, we check if the absolute value of targetDiff is less than the absolute value of smallestDifference (meaning we’ve found a closer sum), or if it’s equal but targetDiff is greater (meaning it’s a larger sum that is equally close). If either condition is true, we update smallestDifference with targetDiff.
  9. Next, we check if targetDiff is greater than 0. If it is, we increment left to try and increase our current triplet sum (since the array is sorted, moving left to the right will increase the sum). If targetDiff is not greater than 0, we decrement right to decrease our triplet sum.
  10. This while loop continues until left and right cross, at which point we have examined all possible triplets for our current value of i.
  11. The for loop continues until we have tried every possible starting point for our triplet.
  12. Once all possible triplets have been considered, the function returns targetSum - smallestDifference. This is the sum of the triplet that was closest to our target sum.

let’s visualize the example 4 via below diagram.

Code

Here is what our algorithm will look like:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
import math

class Solution:
  def searchTriplet(self, arr, target_sum):
    arr.sort()
    smallest_difference = math.inf
    for i in range(len(arr)-2):
      left = i + 1
      right = len(arr) - 1
      while (left < right):
        target_diff = target_sum - arr[i] - arr[left] - arr[right]
        if target_diff == 0:  # we've found a triplet with an exact sum
          return target_sum  # return sum of all the numbers

        # the second part of the following 'if' is to handle the smallest sum when we have
        # more than one solution
        if abs(target_diff) < abs(smallest_difference)  \
              or (abs(target_diff) == abs(smallest_difference) and target_diff > smallest_difference):
          smallest_difference = target_diff  # save the closest and the biggest difference

        if target_diff > 0:
          left += 1  # we need a triplet with a bigger sum
        else:
          right -= 1  # we need a triplet with a smaller sum

    return target_sum - smallest_difference


def main():
  sol = Solution()
  print(sol.searchTriplet([-1, 0, 2, 3], 2))
  print(sol.searchTriplet([-3, -1, 1, 2], 1))
  print(sol.searchTriplet([1, 0, 1, 1], 100))
  print(sol.searchTriplet([0, 0, 1, 1, 2, 6], 5))


main()

Time complexity

Sorting the array will take O(N\ logN)*. Overall searchTriplet() will take O(N \ logN + N^2)*, which is asymptotically equivalent to O(N^2).

Space complexity

The space complexity of the above algorithm will be O(N) which is required for sorting.

Triplets with Smaller Sum (medium)

Design Gurus Educative.io

Problem Statement

Given an array arr of unsorted numbers and a target sum, count all triplets in it such that arr[i] + arr[j] + arr[k] < target where i, j, and k are three different indices. Write a function to return the count of such triplets.

Example 1:

1
2
3
Input: [-1, 0, 2, 3], target=3 
Output: 2
Explanation: There are two triplets whose sum is less than the target: [-1, 0, 3], [-1, 0, 2]

Example 2:

1
2
3
4
Input: [-1, 4, 2, 1, 3], target=5 
Output: 4
Explanation: There are four triplets whose sum is less than the target: 
[-1, 1, 4], [-1, 1, 3], [-1, 1, 2], [-1, 2, 3]

Constraints:

  • n == att.length
  • 0 <= n <= 3500
  • -100 <= arr[i] <= 100
  • -100 <= target <= 100

Solution

This problem follows the Two Pointers pattern and shares similarities with Triplet Sum to Zero. The only difference is that, in this problem, we need to find the triplets whose sum is less than the given target. To meet the condition i != j != k we need to make sure that each number is not used more than once.

Following a similar approach, first we can sort the array and then iterate through it, taking one number at a time. Let’s say during our iteration we are at number ‘X’, so we need to find ‘Y’ and ‘Z’ such that X + Y + Z < target. At this stage, our problem translates into finding a pair whose sum is less than “$ target - X$” (as from the above equation Y + Z == target - X). We can use a similar approach as discussed in Triplet Sum to Zero.

Here’s a detailed walkthrough of the algorithm:

  1. The method searchTriplets starts by sorting the input array arr in ascending order. Sorting is important as it allows us to move our pointers based on the sum we are getting and how close we are to the target sum.
  2. The variable count is initialized to keep track of the total number of triplets found.
  3. The function then iterates through arr using a for loop, stopping when it is two positions from the end of arr (arr.length - 2). This is because we are always looking for triplets and thus don’t need to consider the last two positions in this loop.
  4. Inside the for loop, we call the searchPair function with the array, the target value minus the current element, and the current index. This function will find all pairs within the array from index first+1 to the end of the array whose sum with arr[i] is less than target. The return value, which is the count of such pairs, is added to count.
  5. The searchPair function initializes two pointers: left to first+1 and right to the last element in the array. It then enters a while loop that continues as long as left is less than right.
  6. In the loop, if the sum of the elements at the left and right indices is less than targetSum, this means we have found a valid pair, because adding arr[first] would still result in a sum less than target. Since the array is sorted, all the elements between left and right with arr[first] will also form valid triplets. So, we add all these pairs to our count by adding right - left to count.
  7. We then increment left to move towards higher numbers in the array.
  8. If the sum of the elements at left and right is not less than targetSum, we need a smaller sum. Since the array is sorted, to achieve a smaller sum, we need to reduce the value of the larger number. Hence, we decrement right.
  9. This process repeats until left and right cross, at which point we have examined all possible pairs for our current value of first.
  10. Once searchPair has processed all possible pairs for the given first index, it returns the count of valid pairs.
  11. The loop in searchTriplets continues until we have tried every possible starting point for our triplet.
  12. Once all possible triplets have been considered, the searchTriplets function returns count, the total number of triplets whose sum is less than target.

Let’s visualize the example 2 via diagram below.

Code

Here is what our algorithm will look like:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Solution:
  def searchTriplets(self, arr, target):
    if len(arr) < 3:
      return 0
      
    arr.sort()
    count = 0
    for i in range(len(arr)-2):
      count += self.searchPair(arr, target - arr[i], i)
    return count


  def searchPair(self, arr, target_sum, first):
    count = 0
    left, right = first + 1, len(arr) - 1
    while (left < right):
      if arr[left] + arr[right] < target_sum:  # found the triplet
        # since arr[right] >= arr[left], therefore, we can replace arr[right] by any 
        # number between left and right to get a sum less than the target sum
        count += right - left
        left += 1
      else:
        right -= 1  # we need a pair with a smaller sum
    return count


def main():
  sol = Solution()
  print(sol.searchTriplets([-1, 0, 2, 3], 3))
  print(sol.searchTriplets([-1, 4, 2, 1, 3], 5))


main()

Time complexity

Sorting the array will take O(N * logN). The searchPair() will take O(N)O(N). So, overall searchTriplets() will take O(N * logN + N^2), which is asymptotically equivalent to O(N^2).

Space complexity

Ignoring the space required for the output array, the space complexity of the above algorithm will be O(N) which is required for sorting if we are not using an in-place sorting algorithm.

Similar Problems

Problem: Write a function to return the list of all such triplets instead of the count. How will the time complexity change in this case?

Solution: Following a similar approach, we can create a list containing all the triplets. Here is the code::

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution:
  def triplet_with_smaller_sum(self, arr, target):
    arr.sort()
    triplets = []
    for i in range(len(arr)-2):
      self.search_pair(arr, target - arr[i], i, triplets)
    return triplets


  def search_pair(self, arr, target_sum, first, triplets):
    left = first + 1
    right = len(arr) - 1
    while (left < right):
      if arr[left] + arr[right] < target_sum:  # found the triplet
        # since arr[right] >= arr[left], therefore, we can replace arr[right] by any 
        # number between left and right to get a sum less than the target sum
        for i in range(right, left, -1):
          triplets.append([arr[first], arr[left], arr[i]])
        left += 1
      else:
        right -= 1  # we need a pair with a smaller sum


def main():
  sol = Solution()
  print(sol.triplet_with_smaller_sum([-1, 0, 2, 3], 3))
  print(sol.triplet_with_smaller_sum([-1, 4, 2, 1, 3], 5))


main()

Another simpler approach could be to check every triplet of the array with three nested loops and create a list of triplets that meet the required condition.

Time complexity

Sorting the array will take O(N \ logN)*. The searchPair(), in this case, will take O(N^2); the main while loop will run in O(N) but the nested for loop can also take O(N)O(N) - this will happen when the target sum is bigger than every triplet in the array.

So, overall searchTriplets() will take O(N logN + N^3)*, which is asymptotically equivalent to O(N^3).

Space complexity

Ignoring the space required for the output array, the space complexity of the above algorithm will be O(N) which is required for sorting.

*Subarray Product Less Than K

713. Subarray Product Less Than K Design Gurus

Problem Statement

Given an array with positive numbers and a positive target number, find all of its contiguous subarrays whose product is less than the target number.

Example 1:

1
2
3
Input: [2, 5, 3, 10], target=30                                              
Output: [2], [5], [2, 5], [3], [5, 3], [10]                           
Explanation: There are six contiguous subarrays whose product is less than the target.

Example 2:

1
2
3
Input: [8, 2, 6, 5], target=50                                              
Output: [8], [2], [8, 2], [6], [2, 6], [5], [6, 5]                         
Explanation: There are seven contiguous subarrays whose product is less than the target.

Constraints:

  • 1 <= arr.length <= 3 * 104
  • 1 <= arr[i] <= 1000
  • 0 <= k <= 106

Solution

This problem follows the Sliding Window and the Two Pointers pattern and shares similarities with Triplets with Smaller Sum with two differences:

  1. In this problem, the input array is not sorted.
  2. Instead of finding triplets with sum less than a target, we need to find all subarrays having a product less than the target.

The implementation will be quite similar to Triplets with Smaller Sum. Here is a step-by-step explanation of the algorithm:

  1. The goal of this algorithm is to find all subarrays of a given integer array where the product of the numbers in the subarray is less than a specified target value.
  2. The algorithm uses a sliding window approach combined with a two-pointer method. A “window” of subarray is defined between the indices pointed to by two pointers, left and right.
  3. The window starts from the leftmost side of the array (both left and right at position 0) and slides to the right one element at a time, expanding the window. This expansion is represented by incrementing right.
  4. As we add a new element into the window (the right element), we multiply our current product with this new element.
  5. If at any point the product of the numbers within the window (from left to right) becomes greater than or equal to the target, we need to make the product smaller. This is achieved by moving the left pointer to the right (incrementing left), effectively excluding the left element from our window, and dividing our product by this removed element. We keep doing this until our product is less than target again.
  6. For each position of right, we create all possible subarrays that end at right, and that have a product less than the target. We do this by starting with a subarray that only includes the right element, then progressively adding the element to its left, and so on, until we reach the left pointer. All of these subarrays are added to the result.
  7. This process is repeated for each element in the array (each position of right), with the left boundary being adjusted as necessary.
  8. At the end of this process, result will contain all possible subarrays that have a product less than the target.

In summary, this algorithm slides a window across the array, expanding and contracting this window as necessary, to find all subarrays where the product of the numbers is less than a target value. For each window, it generates all valid subarrays ending at the right edge of the window.

Let’s walkthrough the example 1 through below diagram.

Code

Here is what our algorithm will look like:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
class Solution:
  def findSubarrays(self, arr, target):
      # Resultant list to store all valid subarrays.
      result = []

      # Variable to store the product of elements in the current subarray.
      product = 1.0

      # Left boundary of the current subarray.
      left = 0

      # Iterate over the array using 'right' as the right boundary of the current subarray.
      for right in range(len(arr)):
          # Update the product with the current element.
          product *= arr[right]

          # If the product is greater than or equal to the target, slide the left boundary to 
          # the right until product is less than target.
          while product >= target and left < len(arr):
              product /= arr[left]
              left += 1

          # Create a temporary list to store the current subarray.
          temp_list = []

          # Iterate from 'right' to 'left' and add all these subarrays to the result.
          for i in range(right, left - 1, -1):
              # Add the current element at the beginning of the list.
              temp_list.insert(0, arr[i])

              # Add the current subarray to the result.
              result.append(list(temp_list))

      # Return the result.
      return result


# Example usage
sol = Solution()
print(sol.findSubarrays([2, 5, 3, 10], 30))
print(sol.findSubarrays([8, 2, 6, 5], 50))

Time Complexity

The main for-loop managing the sliding window takes O(N) but creating subarrays can take up to O(N^2) in the worst case. Therefore overall, our algorithm will take O(N^3) .

Space Complexity

Ignoring the space required for the output list, the algorithm runs in space which is used for the temp list.

Can you try estimating how much space will be required for the output list?

1
n + (n-1) + (n-2) + ... 3 + 2 + 1

The worst-case will happen when every subarray has a product less than the target!

So the question will be, how many contiguous subarrays an array can have?
It is definitely not all Permutations of the given array; is it all Combinations of the given array?

It is not all the Combinations of all elements of the array!

For an array with distinct elements, finding all of its contiguous subarrays is like finding the number of ways to choose two indices, i and j, in the array such that i <= j.

If there are a total of n elements in the array, here is how we can count all the contiguous subarrays:

  1. When i = 0, j can have any value from 0 to n-1, giving a total of n choices.
  2. When i = 1, j can have any value from 1 to n-1, giving a total of n-1 choices.
  3. Similarly, when i = 2, j can have n-2 choices. … …
  4. When i = n-1, j can only have only 1 choice.

Let’s combine all the choices:

Which gives us a total of: n * (n + 1) / 2.

So, at most, we need space for O(N^2) output lists. At worst, each subarray can take O(N) space, so overall, our algorithm’s space complexity will be O(N^3).

*Dutch National Flag Problem (medium)

75. Sort Colors Design Gurus Educative.io

Problem Statement

Given an array containing 0s, 1s and 2s, sort the array in-place. You should treat numbers of the array as objects, hence, we can’t count 0s, 1s, and 2s to recreate the array.

The flag of the Netherlands consists of three colors: red, white and blue; and since our input array also consists of three different numbers that is why it is called Dutch National Flag problem.

Example 1:

1
2
Input: [1, 0, 2, 1, 0]
Output: [0 0 1 1 2]

Example 2:

1
2
Input: [2, 2, 0, 1, 2, 0]
Output: [0 0 1 2 2 2 ]

Constraints:

  • n == arr.length
  • 1 <= n <= 300
  • arr[i] is either 0, 1, or 2.

Solution

The brute force solution will be to use an in-place sorting algorithm like Heapsort which will take O(N \ logN)*. Can we do better than this? Is it possible to sort the array in one iteration?

We can use a Two Pointers approach while iterating through the array. Let’s say the two pointers are called low and high which are pointing to the first and the last element of the array respectively. So while iterating, we will move all 0s before low and all 2s after high so that in the end, all 1s will be between low and high. In the end, all 0s are on the left, all 1s are in the middle, and all 2s are on the right.

Here’s a detailed walkthrough of the algorithm:

  1. We start by initializing three variables: low to 0, high to the last index of the array, and i also to 0. Low is meant to keep track of the latest position where a 0 should be placed, high is meant to keep track of the latest position where a 2 should be placed, and i is used to iterate through the array.
  2. We then start a loop that continues as long as i is less than or equal to high. In each iteration of the loop, we check the value of the array at the index i.
  3. If the value is 0, we swap the values at the indices i and low. We then increment both i and low, since we know that the new element at low is 0 (sorted in its correct place) and we can move to the next index.
  4. If the value is 1, we do nothing other than increment i. This is because we want 1s to be in the middle of the array.
  5. If the value is 2, we swap the values at i and high. However, after the swap, we only decrement high without incrementing i. This is because the new value at index i (after the swap) could be 0, 1 or 2, and we need to check this value again in the next iteration.
  6. The swap function simply switches the values at two given indices in the array.
  7. The process continues until i is greater than high, at which point every element in the array has been checked and placed in its correct position. Hence, the array is now sorted.

Let’s consider the example 1 and understand it via visual representation.

Code

Here is what our algorithm will look like:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Solution:
  def sort(self, arr):
    # all elements < low are 0, and all elements > high are 2
    # all elements from >= low < i are 1
    low, high = 0, len(arr) - 1
    i = 0
    while(i <= high):
      if arr[i] == 0:
        arr[i], arr[low] = arr[low], arr[i]
        # increment 'i' and 'low'
        i += 1
        low += 1
      elif arr[i] == 1:
        i += 1
      else:  # the case for arr[i] == 2
        arr[i], arr[high] = arr[high], arr[i]
        # decrement 'high' only, after the swap the number at index 'i' could be 0, 1 or 2
        high -= 1
    return arr

def main():
  sol = Solution()
  arr = [1, 0, 2, 1, 0]
  arr = sol.sort(arr)
  print(arr)

  arr = [2, 2, 0, 1, 2, 0]
  arr = sol.sort(arr)
  print(arr)


main()

Time complexity

The time complexity of the above algorithm will be O(N) as we are iterating the input array only once.

Space complexity

The algorithm runs in constant space O(1).

Problem Challenge 1

18. 4Sum Design Gurus Educative.io

Quadruple Sum to Target (medium)

Given an array of unsorted numbers and a target number, find all unique quadruplets in it, whose sum is equal to the target number.

Example 1:

1
2
3
Input: [4, 1, 2, -1, 1, -3], target=1
Output: [-3, -1, 1, 4], [-3, 1, 1, 2]
Explanation: Both the quadruplets add up to the target.

Example 2:

1
2
3
Input: [2, 0, -1, 1, -2, 2], target=2
Output: [-2, 0, 2, 2], [-1, 0, 1, 2]
Explanation: Both the quadruplets add up to the target.

Constraints:

  • 1 <= nums.length <= 200
  • -109 <= nums[i] <= 109
  • -109 <= target <= 109

Solution

This problem follows the Two Pointers pattern and shares similarities with “Triplet Sum to Zero”.

We can follow a similar approach to iterate through the array, taking one number at a time. At every step during the iteration, we will search for the quadruplets similar to Triplet Sum to Zero whose sum is equal to the given target.

Here’s a detailed walkthrough of the algorithm:

  1. In searchQuadruplets, the array is first sorted in ascending order. Sorting is important as it allows us to navigate our pointers based on the sum we’re calculating and ensures that the generated quadruplets are in a predictable order.
  2. A List named quadruplets is created to store all the quadruplets found.
  3. The algorithm then loops over the array, stopping when there are less than four elements remaining (since we need groups of four).
  4. If the current element is the same as the previous one (and it’s not the first), we skip this iteration to avoid duplicate quadruplets.
  5. A nested loop is initiated from the next index of the outer loop. This loop also ensures that the current element isn’t the same as the previous one to avoid duplicates.
  6. The searchPairs function is called with the array, target value, indices of the first two elements, and the quadruplets list. This function will find pairs in the array (from second+1 index to the end) whose sum with arr[first] and arr[second] equals the target. Any valid quadruplets found are added to the quadruplets list.
  7. In searchPairs, two pointers left and right are initialized: left to second+1, and right to the last element of the array. It then enters a while loop that continues until left is less than right.
  8. Inside this loop, the sum of the elements at the current four indices (first, second, left, right) is calculated. If this sum equals targetSum, a valid quadruplet is found.
  9. This quadruplet is added to the quadruplets list, and both left and right pointers are moved inward. If the next elements are the same as the current elements of left and right respectively, they are skipped to avoid duplicates.
  10. If the calculated sum is less than targetSum, left is incremented to increase the sum (as the array is sorted), and if the sum is greater than targetSum, right is decremented to decrease the sum.
  11. This process repeats until left and right cross, by which point all possible pairs for the given first and second indices have been examined.
  12. Once searchPairs has processed all possible pairs for the given first and second indices, it returns, and the nested loop in searchQuadruplets continues until all possible starting points for quadruplets have been tried.
  13. Once all possible quadruplets have been considered, searchQuadruplets returns the quadruplets list.

The main function in the code demonstrates usage of the searchQuadruplets function with two test cases. It runs searchQuadruplets with specified arrays and target sums, printing the results to the console.

Let’s walkthrough the example 1 through diagram below.

Code

Here is what our algorithm will look like:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
class Solution:
  def searchQuadruplets(self, arr, target):
    arr.sort()
    quadruplets = []
    for i in range(0, len(arr)-3):
      # skip same element to avoid duplicate quadruplets
      if i > 0 and arr[i] == arr[i - 1]:
        continue
      for j in range(i + 1, len(arr)-2):
        # skip same element to avoid duplicate quadruplets
        if j > i + 1 and arr[j] == arr[j - 1]:
          continue
        self.search_pairs(arr, target, i, j, quadruplets)
    return quadruplets


  def search_pairs(self,arr, target_sum, first, second, quadruplets):
    left = second + 1
    right = len(arr) - 1
    while (left < right):
      quad_sum = arr[first] + arr[second] + arr[left] + arr[right]
      if quad_sum == target_sum:  # found the quadruplet
        quadruplets.append(
          [arr[first], arr[second], arr[left], arr[right]])
        left += 1
        right -= 1
        while (left < right and arr[left] == arr[left - 1]):
          left += 1  # skip same element to avoid duplicate quadruplets
        while (left < right and arr[right] == arr[right + 1]):
          right -= 1  # skip same element to avoid duplicate quadruplets
      elif quad_sum < target_sum:
        left += 1  # we need a pair with a bigger sum
      else:
        right -= 1  # we need a pair with a smaller sum


def main():
  sol = Solution()
  print(sol.searchQuadruplets([4, 1, 2, -1, 1, -3], 1))
  print(sol.searchQuadruplets([2, 0, -1, 1, -2, 2], 2))


main()

Time complexity

Sorting the array will take O(NlogN). Overall searchQuadruplets() will take O(N \ logN + N^3)*, which is asymptotically equivalent to O(N^3).

Space complexity

The space complexity of the above algorithm will be O(N) which is required for sorting.

# Problem Challenge 2

844. Backspace String Compare Design Gurus Educative.io

Comparing Strings containing Backspaces (medium)

Given two strings containing backspaces (identified by the character ‘#’), check if the two strings are equal.

Example 1:

1
2
3
Input: str1="xy#z", str2="xzz#"
Output: true
Explanation: After applying backspaces the strings become "xz" and "xz" respectively.

Example 2:

1
2
3
Input: str1="xy#z", str2="xyz#"
Output: false
Explanation: After applying backspaces the strings become "xz" and "xy" respectively.

Example 3:

1
2
3
4
Input: str1="xp#", str2="xyz##"
Output: true
Explanation: After applying backspaces the strings become "x" and "x" respectively.
In "xyz##", the first '#' removes the character 'z' and the second '#' removes the character 'y'.

Example 4:

1
2
3
Input: str1="xywrrmp", str2="xywrrmu#p"
Output: true
Explanation: After applying backspaces the strings become "xywrrmp" and "xywrrmp" respectively.

Constraints:

  • 1 <= str1.length, str2.length <= 200
  • str1 and str2 only contain lowercase letters and ‘#’ characters.

Solution

To compare the given strings, first, we need to apply the backspaces. An efficient way to do this would be from the end of both the strings. We can have separate pointers, pointing to the last element of the given strings. We can start comparing the characters pointed out by both the pointers to see if the strings are equal. If, at any stage, the character pointed out by any of the pointers is a backspace (’#’), we will skip and apply the backspace until we have a valid character available for comparison.

Here’s a detailed walkthrough of the algorithm:

  1. In the compare function, two pointers are initialized, index1 and index2, to the last index of str1 and str2, respectively.
  2. A while loop is started which continues until both pointers are less than zero, that is, both have traversed their strings completely in a reverse manner.
  3. Inside this loop, for each string, the getNextValidCharIndex function is called with the current pointer. This function returns the index of the next valid character in the string (traversing from back to front) by taking into account the backspace characters. i1 and i2 point to the index of the next valid character in the two strings.
  4. If both i1 and i2 are less than zero, it means the end of both strings has been reached, and the strings are considered equal.
  5. If only one of i1 or i2 is less than zero, it means the end of one string has been reached, but not the other, and the strings are not equal.
  6. If the characters at indices i1 and i2 are not the same, the strings are not equal.
  7. If none of the above conditions are met, the loop continues to the next valid characters in both strings.
  8. The getNextValidCharIndex function accepts a string and an index, and uses a backspace count to keep track of how many backspaces have been encountered. It then loops through the string backwards from the provided index until it encounters a valid character or reaches the beginning of the string.
  9. If a backspace character is found, the backspace count is incremented. If a non-backspace character is found and there are any counted backspaces, one backspace is subtracted from the count (to simulate the removal of the previous character), and the loop continues. If a non-backspace character is found and there are no backspaces left to account for, the loop breaks and the index of the valid character is returned.

Here is the visual representation of this algorithm for Example 2:

Code

Here is what our algorithm will look like:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
class Solution:
  def compare(self, str1, str2):
    # use two pointer approach to compare the strings
    index1 = len(str1) - 1
    index2 = len(str2) - 1
    # 注意这里是or ("bbbextm", "bbb#extm")
    while (index1 >= 0 or index2 >= 0):
      i1 = self.get_next_valid_char_index(str1, index1)
      i2 = self.get_next_valid_char_index(str2, index2)
      # 这个if是对于这个例子("ab##", "c#d#")
      if i1 < 0 and i2 < 0:  # reached the end of both the strings
        return True
      if i1 < 0 or i2 < 0:  # reached the end of one of the strings
        return False
      if str1[i1] != str2[i2]:  # check if the characters are equal
        return False

      index1 = i1 - 1
      index2 = i2 - 1

    return True


  def get_next_valid_char_index(self, str, index):
    backspace_count = 0
    while (index >= 0):
      if str[index] == '#':  # found a backspace character
        backspace_count += 1
      elif backspace_count > 0:  # a non-backspace character
        backspace_count -= 1
      else:
        break

      index -= 1  # skip a backspace or a valid character

    return index


def main():
  sol = Solution()
  print(sol.compare("xy#z", "xzz#"))
  print(sol.compare("xy#z", "xyz#"))
  print(sol.compare("xp#", "xyz##"))
  print(sol.compare("xywrrmp", "xywrrmu#p"))


main()


Time complexity

The time complexity of the above algorithm will be O(M+N) where ‘M’ and ‘N’ are the lengths of the two input strings respectively.

Space complexity

The algorithm runs in constant space O(1).

Problem Challenge 3

581. Shortest Unsorted Continuous Subarray Design Gurus Educative.io

Minimum Window Sort (medium)

Given an array, find the length of the smallest subarray in it which when sorted will sort the whole array.

Example 1:

1
2
3
Input: [1, 2, 5, 3, 7, 10, 9, 12]
Output: 5
Explanation: We need to sort only the subarray [5, 3, 7, 10, 9] to make the whole array sorted

Example 2:

1
2
3
Input: [1, 3, 2, 0, -1, 7, 10]
Output: 5
Explanation: We need to sort only the subarray [1, 3, 2, 0, -1] to make the whole array sorted

Example 3:

1
2
3
Input: [1, 2, 3]
Output: 0
Explanation: The array is already sorted

Example 4:

1
2
3
Input: [3, 2, 1]
Output: 3
Explanation: The whole array needs to be sorted.

Constraints:

  • 1 <= arr.length <= 10^4
  • -105 <= arr[i] <= 10^5

Solution

As we know, once an array is sorted (in ascending order), the smallest number is at the beginning and the largest number is at the end of the array. So if we start from the beginning of the array to find the first element which is out of sorting order i.e., which is smaller than its previous element, and similarly from the end of array to find the first element which is bigger than its previous element, will sorting the subarray between these two numbers result in the whole array being sorted?

Let’s try to understand this with Example-2 mentioned above. In the following array, what are the first numbers out of sorting order from the beginning and the end of the array:

1
[1, 3, 2, 0, -1, 7, 10]

Starting from the beginning of the array the first number out of the sorting order is ‘2’ as it is smaller than its previous element which is ‘3’. Starting from the end of the array the first number out of the sorting order is ‘0’ as it is bigger than its previous element which is ‘-1’ As you can see, sorting the numbers between ‘3’ and ‘-1’ will not sort the whole array. To see this, the following will be our original array after the sorted subarray:

1
[1, -1, 0, 2, 3, 7, 10]

The problem here is that the smallest number of our subarray is ‘-1’ which dictates that we need to include more numbers from the beginning of the array to make the whole array sorted. We will have a similar problem if the maximum of the subarray is bigger than some elements at the end of the array. To sort the whole array we need to include all such elements that are smaller than the biggest element of the subarray. So our final algorithm will look like:

  1. From the beginning and end of the array, find the first elements that are out of the sorting order. The two elements will be our candidate subarray.
  2. Find the maximum and minimum of this subarray.
  3. Extend the subarray from beginning to include any number which is bigger than the minimum of the subarray.
  4. Similarly, extend the subarray from the end to include any number which is smaller than the maximum of the subarray.

Here is the visual representation of this algorithm for Example 2:

Code

Here is what our algorithm will look like:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
import math

class Solution:
  def sort(self, arr):
    low, high = 0, len(arr) - 1
    # find the first number out of sorting order from the beginning
    while (low < len(arr) - 1 and arr[low] <= arr[low + 1]):
      low += 1

    if low == len(arr) - 1:  # if the array is sorted
      return 0

    # find the first number out of sorting order from the end
    while (high > 0 and arr[high] >= arr[high - 1]):
      high -= 1

    # find the maximum and minimum of the subarray
    subarray_max = -float('inf')
    subarray_min = float('inf')
    for k in range(low, high+1):
      subarray_max = max(subarray_max, arr[k])
      subarray_min = min(subarray_min, arr[k])

    # extend the subarray to include any number which is bigger than the minimum of 
    # the subarray
    while (low > 0 and arr[low-1] > subarray_min):
      low -= 1
    # extend the subarray to include any number which is smaller than the maximum of 
    # the subarray
    while (high < len(arr)-1 and arr[high+1] < subarray_max):
      high += 1

    return high - low + 1


def main():
  sol = Solution()
  print(sol.sort([1, 2, 5, 3, 7, 10, 9, 12]))
  print(sol.sort([1, 3, 2, 0, -1, 7, 10]))
  print(sol.sort([1, 2, 3]))
  print(sol.sort([3, 2, 1]))


main()

Time complexity

The time complexity of the above algorithm will be O(N).

Space complexity

The algorithm runs in constant space O(1).

Author：Hasuer

Link：https://hasuer.github.io/1-pattern-two-pointers/index.html

Publish date：May 1st 2024, 9:42:18 am

Update date：May 28th 2024, 11:27:15 am

License：本文采用知识共享署名-非商业性使用 4.0 国际许可协议进行许可

CATALOG
  1. 1. Introduction
  2. 2. Pair with Target Sum (easy)
    1. 2.1. Problem Statement
    2. 2.2. Solution
    3. 2.3. Code
    4. 2.4. Time Complexity
    5. 2.5. Space Complexity
    6. 2.6. An Alternate approach
    7. 2.7. Time Complexity
    8. 2.8. Space Complexity
  3. 3. Remove Duplicates (easy)
    1. 3.1. Problem Statement
    2. 3.2. Solution
    3. 3.3. Code
      1. 3.3.1. Time Complexity
      2. 3.3.2. Space Complexity
    4. 3.4. Similar Questions
  4. 4. Squaring a Sorted Array (easy)
    1. 4.1. Problem Statement
    2. 4.2. Solution
    3. 4.3. Code
      1. 4.3.1. Time complexity
      2. 4.3.2. Space complexity
  5. 5. *Triplet Sum to Zero (medium)
    1. 5.1. Problem Statement
    2. 5.2. Solution
    3. 5.3. Code
      1. 5.3.1. Time complexity
      2. 5.3.2. Space complexity
  6. 6. Triplet Sum Close to Target (medium)
    1. 6.1. Problem Statement
    2. 6.2. Solution
    3. 6.3. Code
      1. 6.3.1. Time complexity
      2. 6.3.2. Space complexity
  7. 7. Triplets with Smaller Sum (medium)
    1. 7.1. Problem Statement
    2. 7.2. Solution
    3. 7.3. Code
      1. 7.3.1. Time complexity
      2. 7.3.2. Space complexity
    4. 7.4. Similar Problems
      1. 7.4.1. Time complexity
      2. 7.4.2. Space complexity
  8. 8. *Subarray Product Less Than K
    1. 8.1. Problem Statement
    2. 8.2. Solution
    3. 8.3. Code
    4. 8.4. Time Complexity
    5. 8.5. Space Complexity
  9. 9. *Dutch National Flag Problem (medium)
    1. 9.1. Problem Statement
    2. 9.2. Solution
    3. 9.3. Code
      1. 9.3.1. Time complexity
      2. 9.3.2. Space complexity
  10. 10. Problem Challenge 1
    1. 10.1. Quadruple Sum to Target (medium)
    2. 10.2. Solution
    3. 10.3. Code
      1. 10.3.1. Time complexity
      2. 10.3.2. Space complexity
  11. 11. # Problem Challenge 2
    1. 11.1. Comparing Strings containing Backspaces (medium)
    2. 11.2. Solution
    3. 11.3. Code
      1. 11.3.1. Time complexity
      2. 11.3.2. Space complexity
  12. 12. Problem Challenge 3
    1. 12.1. Minimum Window Sort (medium)
    2. 12.2. Solution
    3. 12.3. Code
      1. 12.3.1. Time complexity
      2. 12.3.2. Space complexity
Total : 41
2024
2022
2021
Interview
技术笔记 Grokking-Interview-Pattern