Hasuer's Studio.

23. Pattern Trie

Grokking Interview Pattern Interview
Word count: 7.6kReading time: 47 min
2024/05/23

Introduction to Trie

Introduction to Trie

A Trie, short for retrieval, is a specialized tree-based data structure primarily used for efficient storing, searching, and retrieval of strings over a given alphabet. It excels in scenarios where a large collection of strings needs to be managed and pattern-matching operations need to be performed with optimal efficiency.

Defining a Trie

A Trie, often referred to as a prefix tree, is constructed to represent a set of strings where each node in the tree corresponds to a single character of a string. The path from the root node to a particular node represents the characters of a specific string. This structural characteristic allows Tries to effectively share common prefixes among strings, leading to efficient storage and retrieval.

In the context of a Trie, the given strings are typically formed from a fixed alphabet. Each edge leading from a parent node to its child node corresponds to a character from the alphabet. By following the path of characters from the root to a specific node, we can reconstruct the string associated with that path.

Let’s look at the below Trie diagram.

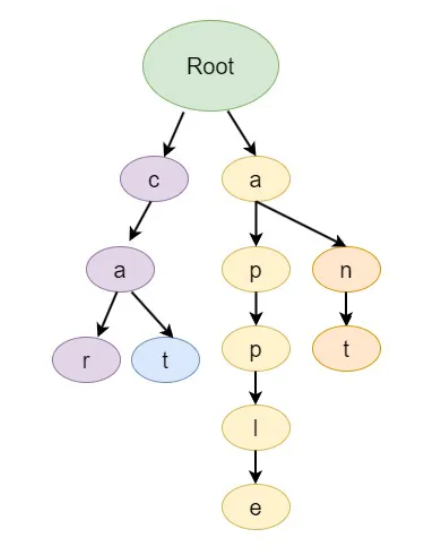
In the above Trie, car and cat shares the common prefix, and apple and ant shares the common prefix.

Need for Trie Data Structure?

Tries are commonly employed in applications such as spell checking, autocomplete suggestions, and searching within dictionaries or databases. They excel at these tasks because they minimize the search complexity in proportion to the length of the target string, making them significantly more efficient than other data structures like binary search trees.

Advantages of Using Tries

  • Fast Pattern Matching: Tries provide rapid pattern matching queries, taking time proportional to the length of the pattern (or the string being searched).
  • Common Prefix Sharing: Strings with common prefixes share nodes in the Trie, leading to efficient memory utilization and reduced redundancy.
  • Efficient Insertion and Deletion: Tries are amenable to dynamic operations like insertion and deletion, while maintaining efficient search times. Alphabet Flexibility: Tries can handle various alphabets, making them versatile for a range of applications.
  • Word Frequency Counting: Tries can be extended to store additional information at nodes, such as the frequency of words or strings.

In comparison to using a binary search tree, where a well-balanced tree would require time proportional to the product of the maximum string length and the logarithm of the number of keys, Tries offer the advantage of a search time linearly dependent on the length of the string being searched. This results in an optimization of search operations, especially when dealing with large datasets.

In summary, a Trie is a powerful data structure that optimizes string-related operations by efficiently storing and retrieving strings with shared prefixes. Its unique structure and fast search capabilities make it an invaluable tool in various text-based applications.

Properties of the Trie Data Structure

Trie is a tree-like data structure. So, it’s important to know the properties of Trie.

  1. Single Root Node: Every trie has one root node, serving as the starting point for all strings stored within.
  2. Node as a String: In a trie, each node symbolizes a string, with the path from the root to that node representing the string in its entirety.
  3. Edges as Characters: The edges connecting nodes in a trie represent individual characters. This means that traversing an edge essentially adds a character to the string.
  4. Node Structure: Nodes in a trie typically contain either hashmaps or arrays of pointers. Each position in this array or hashmap corresponds to a character. Additionally, nodes have a flag to signify if a string concludes at that particular node.
  5. Character Limitation: While tries can accommodate a vast range of characters, for the purpose of this discussion, we’re focusing on lowercase English alphabets (a-z). This means each node will have 26 pointers, with the 0th pointer representing ‘a’ and the 25th one representing ‘z’.
  6. Path Equals Word: In a trie, any path you trace from the root node to another node symbolizes a word or a string. This makes it easy to identify and retrieve strings.

These properties underline the essence of the trie data structure, emphasizing its efficiency and utility in managing strings, especially when dealing with large datasets.

Implementation of Tries

Let’s start by understanding the basic implementation of a Trie. Each node in a Trie can have multiple children, each representing a character. To illustrate this, consider the following simple Trie structure:

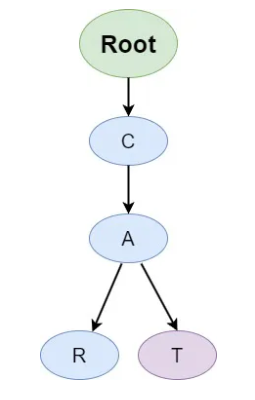
Here’s a step-by-step guide to implement a Trie:

  • The Trie starts from the root node.
  • The path from the root to the node “c” represents the character “c.”
  • The path from “c” to “a” represents the string “ca,” and from “a” to “r” represents the string “car.”
  • The path from “c” to “a” represents the string “ca,” and from “a” to “t” represents the string “cat.”

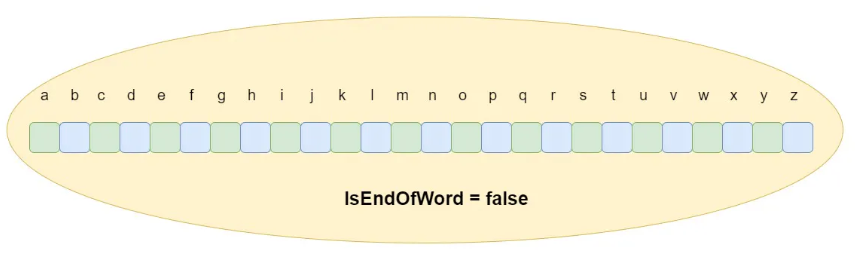
Representation of Trie Node

The Trie node has an array or list of children nodes, typically of size 26 to represent the English lowercase alphabets (a-z). Additionally, there’s a boolean flag isEndOfWord to indicate whether the current node marks the end of a word in the Trie.

1
2
3
4
5
class TrieNode:
    def __init__(self):
        self.children = [None]*26
        self.isEndOfWord = False

Now, let’s look at the basic operations such as insertion, searching, and deletion on the Trie data structure.

Insertion in Trie Data Structure

Insertion in a Trie involves adding a string to the Trie, character by character, starting from the root. If the character already exists in the Trie, we move to the next node; otherwise, we create a new node for the character.

Algorithm
  1. Start from the root node.
  2. For each character in the string:
    • Check if the character exists in the current node’s children.
    • If it exists, move to the corresponding child node.
    • If it doesn’t exist, create a new node for the character and link it to the current node.
    • Move to the newly created node.
  3. After processing all characters in the string, mark the current node as the end of the word.
Example

Consider that we need to insert the ‘can’, ‘cat’, ‘cant’, and ‘apple’ into the trie. We insert them in the following order:

  1. Initial Trie:
1
Root
  1. Insert ‘can’:
1
2
3
4
5
6
7
Root
 |
 c
 |
 a
 |
 n

Explanation: Starting from the root, we add nodes for each character in “can”.

  1. Insert ‘cat’:
1
2
3
4
5
6
7
Root
 |
 c
 |
 a
 | \
 n   t

Explanation: “cat” shares the first two characters with “can”, so we just add a new branch for the ‘t’ after ‘a’.

  1. Insert ‘cant’:
1
2
3
4
5
6
7
8
9
Root
 |
 c
 |
 a
 | \
 n   t
 |
 t

Explanation: “cant” extends from the path of “can”, so we add a new node for ‘t’ after the existing ‘n’.

  1. Insert ‘apple’:
1
2
3
4
5
6
7
8
9
10
11
Root
 |   \
 c     a
 |     |
 a     p
 | \   |
 t   n p
 |     |
 t     l
       |
       e

Explanation: Starting from the root, we add nodes for each character in “apple” branching from the ‘a’ node.

Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class TrieNode:
    def __init__(self):
        self.children = [None] * 26  # Assuming only lowercase English letters
        self.isEndOfWord = False

class Trie:
    def __init__(self):
        self.root = TrieNode()

    def charToIndex(self, ch):
        # Convert character to index (0-25)
        return ord(ch) - ord('a')

    def insert(self, word):
        node = self.root
        for char in word:
            index = self.charToIndex(char)
            if not node.children[index]:
                node.children[index] = TrieNode()
            node = node.children[index]
        node.isEndOfWord = True
Complexity Analysis

Time Complexity: O(n) - Where n is the length of the word. This is when the word doesn’t share any prefix with the words already in the Trie or is longer than any word in the Trie.

Space Complexity:

  • Best Case: O(1) - When the word is entirely a prefix of an existing word or shares a complete prefix with words in the Trie.
  • Worst Case: O(n) - When the word doesn’t share any characters with the words in the Trie.

Searching in Trie Data Structure

Searching into Trie is similar to the insertion into the Trie. Let’s look at the below algorithm to search in the Trie data structure.

Algorithm
  1. Start from the root node.
  2. For each character in the word: a. Calculate its index (e.g., ‘a’ is 0, ‘b’ is 1, …). b. Check if the corresponding child node exists. c. If it exists, move to the child node and continue. d. If it doesn’t exist, return false (word not found).
  3. After processing all characters, check the isEndOfWord flag of the current node. If it’s true, the word exists in the Trie; otherwise, it doesn’t.
Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class TrieNode:
    def __init__(self):
        self.children = [None] * 26  # Children nodes
        self.isEndOfWord = False  # Flag to represent the end of a word

class Trie:
    def __init__(self):
        self.root = TrieNode()

    # Function to search a word in the Trie
    def search(self, word):
        node = self.root
        for char in word:
            index = ord(char) - ord('a')
            if not node.children[index]:
                return False  # Word not found
            node = node.children[index]
        return node.isEndOfWord  # Return true if word exists, false otherwise

Complexity Analysis

Time Complexity: O(n) - Where n is the length of the word. This happens when you have to traverse the Trie to the deepest level.

Space Complexity: O(1) - Searching doesn’t require any additional space as it’s just about traversing the Trie.

Deletion in Trie Data Structure

When we delete a key in a Trie, there are three cases to consider:

  1. Key is a leaf node: If the key is a leaf node, we can simply remove it from the Trie.
  2. Key is a prefix of another key: If the key is a prefix of another key in the Trie, then we cannot remove it entirely. Instead, we just unmark the isEndOfWord flag.
  3. Key has children: If the key has children, we need to recursively delete the child nodes. If a child node becomes a leaf node after the deletion of the key, we can remove the child node as well.
Algorithm
  1. Initialization:
    • Start from the root of the Trie.
    • Begin with the first character of the word you want to delete.
  2. Base Case:
    • If you’ve reached the end of the word:
      • Check if the current node has the isEndOfWord flag set to true. If not, the word doesn’t exist in the Trie, so return false.
      • If the flag is true, unset it. This means the word is no longer recognized as a word in the Trie.
      • Check if the current node has any children. If it doesn’t, it means this node doesn’t contribute to any other word in the Trie, so it can be safely deleted. Return true to indicate to its parent that it can be removed.
  3. Recursive Case:
    • For the current character in the word:
      • Calculate its index (e.g., ‘a’ is 0, ‘b’ is 1, …).
      • Check if the corresponding child node exists. If it doesn’t, the word is not present in the Trie, so return false.
      • If the child node exists, make a recursive call to the delete function with the child node and the next character in the word.
  4. Post-Recursive Handling:
    • After the recursive call, check the return value:
      • If it’s true, it means the child node can be deleted. Remove the reference to the child node.
      • Check the current node. If it doesn’t have any other children and its isEndOfWord flag is not set, it means this node doesn’t contribute to any word in the Trie. Return true to indicate to its parent that it can be removed.
      • If the node has other children or its isEndOfWord flag is set, return false.
  5. Completion:
    • Once all characters in the word have been processed, the word will either be deleted from the Trie (if it existed) or the Trie will remain unchanged (if the word didn’t exist).
Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class TrieNode:
    def __init__(self):
        self.children = [None] * 26  # Children nodes
        self.isEndOfWord = False  # Flag to represent the end of a word

class Trie:
    def __init__(self):
        self.root = TrieNode()

    # Recursive function to delete a key from the Trie
    def _delete(self, current, word, index):
        if index == len(word):
            if current.isEndOfWord:
                current.isEndOfWord = False
                return not any(current.children)
            return False

        ch = word[index]
        node = current.children[ord(ch) - ord('a')]
        if not node:
            return False

        shouldDeleteChild = self._delete(node, word, index + 1)
        if shouldDeleteChild:
            current.children[ord(ch) - ord('a')] = None
            return not any(current.children)

        return False

    # Function to delete a word from the Trie
    def deleteWord(self, word):
        self._delete(self.root, word, 0)

Complexity Analysis

Time Complexity: O(n) - Where n is the length of the word. This is when you have to traverse the Trie to the deepest level and potentially backtrack to delete nodes.

Space Complexity: O(1) - Deletion, like searching, doesn’t require any additional space.

Implement Trie (Prefix Tree)

Top Interview 150 | 208. Implement Trie (Prefix Tree) Design Gurus

Problem Statement

Design and implement a Trie (also known as a Prefix Tree). A trie is a tree-like data structure that stores a dynamic set of strings, and is particularly useful for searching for words with a given prefix.

Implement the Solution class:

  • Solution() Initializes the object.
  • void insert(word) Inserts word into the trie, making it available for future searches.
  • bool search(word) Checks if the word exists in the trie.
  • bool startsWith(word) Checks if any word in the trie starts with the given prefix.

Examples

  1. Example 1:
    • Input:
      • Trie operations: ["Trie", "insert", "search", "startsWith"]
      • Arguments: [[], ["apple"], ["apple"], ["app"]]
    • Expected Output: [-1, -1, 1, 1]
    • Justification: After inserting “apple”, “apple” exists in the Trie. There is also a word that starts with “app”, which is “apple”.
  2. Example 2:
    • Input:
      • Trie operations: ["Trie", "insert", "search", "startsWith", "search"]
      • Arguments: [[], ["banana"], ["apple"], ["ban"], ["banana"]]
    • Expected Output: [-1, -1, 0, 1, 1]
    • Justification: After inserting “banana”, “apple” does not exist in the Trie but a word that starts with “ban”, which is “banana”, does exist.
  3. Example 3:
    • Input:
      • Trie operations: ["Trie", "insert", "search", "search", "startsWith"]
      • Arguments: [[], ["grape"], ["grape"], ["grap"], ["gr"]]
    • Expected Output: [-1, -1, 1, 1, 1]
    • Justification: After inserting “grape”, “grape” exists in the Trie. There are words that start with “grap” and “gr”, which is “grape”.

Constraints:

  • 1 <= word.length, prefix.length <= 2000
  • word and prefix consist only of lowercase English letters.
  • At most 3 * 104 calls in total will be made to insert, search, and startsWith.

Solution

The trie is represented as a tree, where each node contains an array of pointers (or references) to its children and a boolean flag indicating if the current node marks the end of a word. When inserting or searching for a word, we start at the root node and navigate through the tree character by character until we either finish the operation or determine the word doesn’t exist in the trie.

Now, let’s break down the operations:

  1. Insert:
    • We begin at the root node.
    • For every character in the word, check if there’s a child node for it.
    • If the child node doesn’t exist, we create it.
    • Navigate to the child node and repeat the process for the next character.
    • Once the end of the word is reached, mark the current node as an endpoint of a word.
  2. Search:
    • Starting at the root, traverse the trie character by character.
    • For every character in the word, check if there’s a child node for it.
    • If at any point there isn’t a child node for the character, the word doesn’t exist in the trie.
    • If we can traverse the entire word and the last node is marked as an endpoint, the word exists in the trie.
  3. StartsWith:
    • The operation is similar to the search, but we don’t need the last node to be an endpoint.
    • If we can traverse the prefix without any missing nodes, there exists a word in the trie that starts with the given prefix.

Algorithm Walkthrough

Using Example 1:

  • ["Trie", "insert", "search", "startsWith"]
  • [[], ["apple"], ["apple"], ["app"]]
  1. Create an empty Trie.
  2. Insert “apple”.
    • Start from the root. For ‘a’, move to the child node or create one if it doesn’t exist.
    • Move to ‘p’, then the next ‘p’, followed by ‘l’ and finally ‘e’. Mark ‘e’ as the end of a word.
  3. Search for “apple”.
    • Start from the root and traverse nodes ‘a’ -> ‘p’ -> ‘p’ -> ‘l’ -> ‘e’. Since ‘e’ is marked as the end of a word, return true.
  4. Check if a word starts with “app”.
    • Traverse nodes for ‘a’ -> ‘p’ -> ‘p’. All nodes exist, so return true.

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
# class TrieNode:
#     def __init__(self):
#         self.children = {}  # Dictionary to store child nodes.
#         self.isEnd = False  # Flag to represent end of a word.

class Solution:
    def __init__(self):
        self.root = TrieNode()

    # Inserts a word into the trie.
    def insert(self, word: str) -> None:
        node = self.root
        for char in word:
            if char not in node.children:
                node.children[char] = TrieNode()
            node = node.children[char]
        node.isEnd = True

    # Returns if the word is in the trie.
    def search(self, word: str) -> bool:
        node = self.root
        for char in word:
            if char not in node.children:
                return False
            node = node.children[char]
        return node.isEnd

    # Returns if there is any word in the trie that starts with the given prefix.
    def startsWith(self, prefix: str) -> bool:
        node = self.root
        for char in prefix:
            if char not in node.children:
                return False
            node = node.children[char]
        return True


if __name__ == "__main__":
    trie = Solution()
    trie.insert("apple")
    print(trie.search("apple"))  # True
    print(trie.search("app"))  # False
    print(trie.startsWith("app"))  # True

Complexity Analysis

  • Time Complexity:
    • Insert: (O(m)), where (m) is the key length.
    • Search and StartsWith: (O(m)) in the worst case scenario.
  • Space Complexity: (O(n \times m)), where (n) is the number of inserted keys and (m) is the average key length.

Index Pairs of a String

Leetcode 会员 Design Gurus

Problem Statement

Given a string text and a list of strings words, identify all [i, j] index pairs such that the substring text[i...j] is in words.

These index pairs should be returned in ascending order, first by the start index, then by the end index. Find every occurrence of each word within the text, ensuring that overlapping occurrences are also identified.

Examples

    • Input: text = "bluebirdskyscraper", words = ["blue", "bird", "sky"]
    • Expected Output: [[0, 3], [4, 7], [8, 10]]
    • Justification: The word “blue” is found from index 0 to 3, “bird” from 4 to 7, and “sky” from 8 to 10 in the string.
    • Input: text = "programmingisfun", words = ["pro", "is", "fun", "gram"]
    • Expected Output: [[0, 2], [3, 6], [11, 12], [13, 15]]
    • Justification: “pro” is found from 0 to 2, “gram” from 3 to 6, “is” from 11 to 12, and “fun” from 13 to 15.
    • Input: text = "interstellar", words = ["stellar", "star", "inter"]
    • Expected Output: [[0, 4], [5, 11]]
    • Justification: “inter” is found from 0 to 4, and “stellar” from 5 to 11. “star” is not found.

Constraints:

  • 1 <= text.length <= 100
  • 1 <= words.length <= 20
  • 1 <= words[i].length <= 50
  • text and words[i] consist of lowercase English letters.
  • All the strings of words are unique.

Solution

To solve this problem, we will use a trie data structure, which is particularly efficient for managing a set of strings and performing quick searches for patterns within a text. A trie, also known as a prefix tree, allows us to efficiently store and retrieve strings with a common prefix, making it ideal for our purpose of identifying substrings within a given text.

The approach involves two main phases: building the trie with the given list of words and then using it to find the index pairs in the text. The trie’s structure enables us to search for each word in the text in an optimized manner, significantly reducing the number of comparisons needed compared to brute force methods.

Step-by-Step Algorithm

  1. Initialize the Trie:
    • Create a trie and insert all the words from the given list into it. This is done in the first part of the code.
  2. Search and Record Index Pairs:
    • Iterate over each character in the text. This character will act as the starting point for potential matches.
    • For each starting character, initiate a pointer p at the root of the trie.
    • Then, iterate over the text starting from the current starting point until the end of the text. In each iteration:
      • Check if the current character exists as a child of the current trie node pointed by p.
      • If it does not exist, break out of the inner loop as no further matching is possible from this starting point.
      • If it exists, move the pointer p to this child node.
      • Check if the current node p is a leaf node (indicated by p.isEnd being true). If it is, it means a complete word from the list has been found.
      • Record the start and end indices of this word. The start index is the position of the starting character, and the end index is the current position in the text.
    • Continue this process for each character in the text to ensure all occurrences, including overlapping ones, are found.

Algorithm Walkthrough

Using the input text = "programmingisfun", words = ["pro", "is", "fun", "gram"]:

  1. Initialize the Trie with Words:
    • “pro”, “is”, “fun”, and “gram” are inserted into the trie.
  2. Search and Record Index Pairs:
    • Start at index 0 ('p' in "programmingisfun"):
      • Pointer p is at the root. Finds ‘p’, moves to ‘r’, then ‘o’. p.isEnd is true at ‘o’, so record [0, 2].
    • At index 1 ('r'), no match is found.
    • similarly, At index 2 ('o'), no match is found.
    • At index 3 ( 'g' ):
      • Finds ‘g’, ‘r’, ‘a’, ‘m’. p.isEnd is true at ‘m’, so record [3, 6].
    • At index 11 ( 'i' ):
      • Finds ‘i’, ‘s’. p.isEnd is true at ‘s’, so record [11, 12].
    • At index 13 ( 's' ):
      • Finds ‘f’, ‘u’, ‘n’. p.isEnd is true at ‘n’, so record [13, 15].
  3. Compile Results:
    • The results [[0, 2], [3, 6], [11, 12], [13, 15]] are compiled into the 2D array ans and returned.

By following these steps, the algorithm efficiently locates all occurrences of the words in the text, including overlapping ones, using the trie structure for optimized searching.

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
class TrieNode:
    def __init__(self):
        self.children = {}  # Using a dictionary to hold child nodes for each letter
        self.isEnd = False  # Flag to mark the end of a word

class Trie:
    def __init__(self):
        self.root = TrieNode()

    # Inserts a word into the trie
    def insert(self, word):
        cur = self.root
        for c in word:
            if c not in cur.children:
                cur.children[c] = TrieNode()  # Create a new node if not present
            cur = cur.children[c]
        cur.isEnd = True  # Mark the end of a word

class Solution:
    def indexPairs(self, text, words):
        trie = Trie()
        # Populate the trie with the list of words
        for word in words:
            trie.insert(word)

        result = []
        for i in range(len(text)):
            p = trie.root
            for j in range(i, len(text)):
                currentChar = text[j]
                if currentChar not in p.children:
                    break  # Break if the character is not in the trie
                p = p.children[currentChar]
                if p.isEnd:
                    result.append([i, j])  # Add index pair if word found as a list

        return result  # Return a list of lists containing index pairs

# Example usage:
solution = Solution()
text1 = "bluebirdskyscraper"
words1 = ["blue", "bird", "sky"]
print(solution.indexPairs(text1, words1))

text2 = "programmingisfun"
words2 = ["pro", "is", "fun", "gram"]
print(solution.indexPairs(text2, words2))

text3 = "interstellar"
words3 = ["stellar", "star", "inter"]
print(solution.indexPairs(text3, words3))

Time and Space Complexity Analysis

Time Complexity:

  • Building the Trie: O(N \ L)*, where N is the number of words and L is the average length of these words.
  • Finding Index Pairs: O(T^2), where T is the length of the text string.
  • Overall: O(N \ L + T^2)*

Space Complexity:

  • Trie Storage: O(N L)*, for storing N words each of average length L.

Design Add and Search Words Data Structure

Top Interview 150 | 211. Design Add and Search Words Data Structure Design Gurus

Problem Statement

Design a data structure that supports the addition of new words and the ability to check if a string matches any previously added word.

Implement the Solution class:

  • Solution() Initializes the object.
  • void addWord(word) Inserts word into the data structure, making it available for future searches.
  • bool search(word) Checks if there is any word in the data structure that matches word. The method returns true if such a match exists, otherwise returns false.

Note: In the search query word, the character '.' can represent any single letter, effectively serving as a wildcard character.

Examples

Example 1:

  • Input:

    1
    2
    ["Solution", "addWord", "addWord", "search", "search"]
    [[], ["apple"], ["banana"], ["apple"], ["....."]]

  • Expected Output:

    1
    [-1, -1, -1, 1, 1]

  • Justification: After adding the words “apple” and “banana”, searching for “apple” will return true since “apple” is in the data structure. Searching for “…..” will also return true as both “apple” and “banana” match the pattern.

Example 2:

  • Input:

    1
    2
    ["Solution", "addWord", "addWord", "search", "search"]
    [[], ["cat"], ["dog"], ["c.t"], ["d..g"]]

  • Expected Output:

    1
    [-1, -1, -1, 1, 0]

  • Justification: “c.t” matches “cat” and “d..g” doesn’t matches “dog”.

Example 3:

  • Input:

    1
    2
    ["Solution", "addWord", "search", "search"]
    [[], ["hello"], ["h.llo"], ["h...o"]]

  • Expected Output:

    1
    [-1, -1, 1, 0]

  • Justification: “h.llo” and “h…o” both match “hello”.

Constraints:

  • 1 <= word.length <= 25
  • word in addWord consists of lowercase English letters.
  • word in search consist of ‘.’ or lowercase English letters.
  • There will be at most 2 dots in word for search queries.
  • At most 104 calls will be made to addWord and search.

Solution

The crux of the problem lies in efficiently inserting words and then searching for them, even if the query includes wildcards. To solve this, we utilize the trie (prefix tree) data structure. A trie is a tree-like structure that’s useful for storing a dynamic set of strings, especially when the dataset involves large numbers of queries on prefixes of strings. Each node of the trie can represent a character of a word, and the path from the root node to any node represents the word stored up to that point. The key operation for the wildcard is a recursive search, which allows us to explore multiple paths in the trie when we encounter the wildcard character.

1. Trie Data Structure: Every node of the trie contains multiple child nodes (one for each character of the alphabet). We start with a root node that represents an empty string. Each level of the trie represents the next character of a word.

2. Adding a Word: To insert a word into our trie, we begin at the root and traverse down the trie based on the characters in the word. If a particular character doesn’t have a corresponding child node in the current node, we create a new child node for that character. Once we’ve processed every character of the word, we mark the final node as the end of a valid word.

3. Searching: Searching for a word is similar to inserting, but with an additional consideration for the wildcard character (‘.’). If we encounter a ‘.’, we must consider all child nodes of the current node and recursively continue our search from each of them. If any of the paths result in a match, we return true. If we reach the end of a word without encountering any mismatches or premature ends, we’ve found a valid word in our trie.

This trie-based approach ensures efficient operations for both inserting and searching for words. In cases without wildcards, the search operation can be performed in linear time relative to the word’s length. However, with wildcards, the time complexity might increase, but the trie structure still ensures that we do this efficiently.

Algorithm Walkthrough

Given the word “apple” to insert and then search for “…..”:

  1. Start at the root node.
  2. For inserting “apple”:
    • At ‘a’, move down or create a node if it doesn’t exist.
    • At ‘p’, move down or create.
    • Do the same for the next ‘p’, ‘l’, and ‘e’.
    • Mark the last node (for ‘e’) as the end of a word.
  3. For searching “…..”:
    • At the first ‘.’, check all child nodes and continue.
    • Repeat for each ‘.’.
    • If any path leads to a node that represents the end of a word, return true.

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
# class TrieNode:
#     def __init__(self):
#         # Initialize children as a dictionary to represent all possible next characters.
#         self.children = {}  
#         # Flag to check if the current node marks the end of any word.
#         self.isEnd = False  

class Solution:

    def __init__(self):
        # Initialize the root node.
        self.root = TrieNode()

    def addWord(self, word: str):
        node = self.root
        for ch in word:
            # If current character isn't already a child of the node, add it.
            if ch not in node.children:
                node.children[ch] = TrieNode()
            # Move on to the next character/node.
            node = node.children[ch]
        # After processing all characters of the word, mark the current node as end of a word.
        node.isEnd = True

    def search(self, word: str) -> bool:
        return self.searchInNode(word, self.root)

    def searchInNode(self, word: str, node: TrieNode) -> bool:
        for i, ch in enumerate(word):
            # Check for wildcard character.
            if ch == '.':
                # Recursively search for all possible characters in place of the wildcard.
                return any(self.searchInNode(word[i + 1:], node.children[child]) for child in node.children if child)
            # If character doesn't exist in children, word can't exist in the trie.
            if ch not in node.children:
                return False
            # Move to the next character/node.
            node = node.children[ch]
        # After processing all characters of the word, return if it's a valid word.
        return node.isEnd


# Test the algorithm
obj = Solution()
obj.addWord("apple")
obj.addWord("banana")
print(obj.search("apple"))  # True
print(obj.search("....."))  # True

Complexity Analysis

  • Time Complexity:
    • Insertion (addWord): O(n), where n is the length of the word. This is because each insertion operation runs in linear time with respect to the length of the word.
    • Search: O(n * m) in the worst case, where n is the length of the word and m is the total number of nodes in the Trie. This happens when the search word contains dots (‘.’). However, for words without dots, the search is O(n).
  • Space Complexity: O(m n), where m is the total number of Trie nodes and n is the average number of characters in the words. Each Trie node has up to 26 children (for each letter of the alphabet). In the worst case, when no nodes are shared, the space complexity is O(m n).

# Extra Characters in a String

2707. Extra Characters in a String Design Gurus

没咋看懂

Problem Statement

Given a string s and an array of words words. Break string s into multiple non-overlapping substrings such that each substring should be part of the words. There are some characters left which are not part of any substring.

Return the minimum number of remaining characters in s, which are not part of any substring after string break-up.

Examples

  1. Example 1:
    • Input: s = "amazingracecar", dictionary = ["race", "car"]
    • Expected Output: 7
    • Justification: The string s can be rearranged to form “racecar”, leaving ‘a’, ‘m’, ‘a’, ‘z’, ‘i’, ‘n’, ‘g’ as extra.
  2. Example 2:
    • Input: s = "bookkeeperreading", dictionary = ["keep", "read"]
    • Expected Output: 9
    • Justification: The words “keep” and “read” can be formed from s, but ‘b’, ‘o’, ‘o’, ‘k’, ‘e’, ‘r’, ‘i’, ‘n’, ‘g’ are extra.
  3. Example 3:
    • Input: s = "thedogbarksatnight", dictionary = ["dog", "bark", "night"]
    • Expected Output: 6
    • Justification: The words “dog”, “bark”, and “night” can be formed, leaving ‘t’, ‘h’, ‘e’, ‘s’, ‘a’, ‘t’ as extra characters.

Constraints:

  • 1 <= str.length <= 50
  • 1 <= dictionary.length <= 50
  • 1 <= dictionary[i].length <= 50
  • dictionary[i] and s consists of only lowercase English letters
  • dictionary contains distinct words

Solution

The solution approach utilizes a dynamic programming strategy combined with a trie data structure. The dynamic programming aspect allows for efficiently keeping track of the minimum extra characters required at each position in the string s. This is achieved by building a bottom-up solution, where we start from the end of the string and work our way towards the beginning, calculating the minimum extra characters required for each substring.

The trie data structure is used to efficiently find and match the words from the dictionary within the string s. The combination of these two methods ensures that the solution is both time-efficient and space-efficient, as it avoids redundant computations and efficiently manages the storage of the dictionary words.

Step-by-Step Algorithm

  1. Initialize Trie:
    • Construct a trie using the words from the dictionary. Each node in the trie represents a character, and a complete path from the root to a leaf node represents a word.
  2. Dynamic Programming Array:
    • Initialize a dynamic programming (DP) array, dp, of length n + 1, where n is the length of the string s. This array will store the minimum number of extra characters required for the substring starting from each index.
  3. DP Calculation:
    • Iterate backwards through the string s:
      • Set dp[start] to dp[start + 1] + 1 initially. This represents the case where the current character is considered an extra character.
      • For each start position, iterate through the string to check if a word in the trie can be formed starting from this position.
      • If the current substring matches a word in the trie (node.isEnd is true), update dp[start] to be the minimum of its current value and dp[end + 1], where end is the end of the matched word. This step ensures that we consider removing the matched word and count the rest as extra characters.
  4. Return Result:
    • The value of dp[0] gives the minimum number of extra characters in the entire string s.

Algorithm Walkthrough

Let’s consider the input s = "bookkeeperreading", dictionary = ["keep", "read"]

  1. Trie Construction:
    • Build the trie with “keep” and “read”.
  2. DP Initialization:
    • Initialize dp array of length 18 (since “bookkeeperreading” has 17 characters).
  3. DP Calculation:
    • Start from index 16 (last character ‘g’):
      • For each index, try to form a word from the trie. For example, at index 12, the word “read” can be formed.
      • Update dp[12] to be the minimum of dp[12] and dp[16] (which is the end of “read” + 1).
  4. Iterate Backwards:
    • Continue this process for each character in s. If a character does not form a word in the trie, dp[start] remains dp[start + 1] + 1.
  5. Final Result:
    • dp[0] will have the minimum extra characters after processing the entire string.

This approach systematically checks each substring of s against the trie, and the dynamic programming array efficiently keeps track of the minimum extra characters required. The use of a trie ensures that each substring check is done in an optimized manner, avoiding unnecessary recomputations.

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
class TrieNode:
    def __init__(self):
        self.children = {}  # Represents each character of the alphabet.
        self.isEnd = False  # To determine if the current TrieNode marks the end of a word.


class Solution:
    def minExtraChar(self, s, dictionary):
        root = self.buildTrie(dictionary)  # Building the trie from the dictionary.
        n = len(s)
        dp = [0] * (n + 1)  # DP array to store minimum extra characters.

        # 从后往前是因为这样适合Trie的结构来进行search
        for start in range(n - 1, -1, -1):
            dp[start] = dp[start + 1] + 1  # Default case: considering current character as extra.

            node = root
            for end in range(start, n):
                if s[end] not in node.children:
                    break  # No further word can be formed.
                node = node.children[s[end]]
                if node.isEnd:
                    dp[start] = min(dp[start], dp[end + 1])

        return dp[0]  # Minimum extra characters for the entire string.

    def buildTrie(self, dictionary):
        root = TrieNode()
        for word in dictionary:
            node = root
            for char in word:
                if 'a' <= char <= 'z':  # Ensure the character is a lowercase letter
                    if char not in node.children:
                        node.children[char] = TrieNode()  # Creating new node if not exists.
                    node = node.children[char]
                else:
                    raise ValueError(f"Invalid character {char} in dictionary word {word}")
            node.isEnd = True  # Mark the end of a word.
        return root


def main():
    solution = Solution()
    print(solution.minExtraChar("amazingracecar", ["race", "car"]))  # Output: 7
    print(solution.minExtraChar("bookkeeperreading", ["keep", "read"]))  # Output: 9
    print(solution.minExtraChar("thedogbarksatnight", ["dog", "bark", "night"]))  # Output: 6


if __name__ == "__main__":
    main()

Time and Space Complexity Analysis

Time Complexity

  • Trie Construction: (O(W * L)), where (W) is the number of words in the dictionary and (L) is the average length of these words.
  • Dynamic Programming Calculation: (O(n^2)), where (n) is the length of the input string s.
  • Total Time Complexity: (O(W * L + n^2)).

Space Complexity

  • Trie Storage: (O(W * L)), for storing the words in the trie.
  • Dynamic Programming Array: (O(n)), for the array used in dynamic programming.
  • Total Space Complexity: (O(W * L + n)).

Search Suggestions System

1268. Search Suggestions System Design Gurus

不如暴力解法，看leetcode上之前用java写的

Problem Statement

Given a list of distinct strings products and a string searchWord.

Determine a set of product suggestions after each character of the search word is typed. Every time a character is typed, return a list containing up to three product names from the products list that have the same prefix as the typed string.

If there are more than 3 matching products, return 3 lexicographically smallest products. These product names should be returned in lexicographical (alphabetical) order.

Examples

  1. Example 1:
    • Input: Products: [“apple”, “apricot”, “application”], searchWord: “app”
    • Expected Output: [[“apple”, “apricot”, “application”], [“apple”, “apricot”, “application”], [“apple”, “application”]]
    • Justification: For the perfix ‘a’, “apple”, “apricot”, and “application” match. For the prefix ‘ap’, “apple”, “apricot”, and “application” match. For the prefix ‘app’, “apple”, and “application” match
  2. Example 2:
    • Input: Products: [“king”, “kingdom”, “kit”], searchWord: “ki”
    • Expected Output: [[“king”, “kingdom”, “kit”], [“king”, “kingdom”, “kit”]]
    • Justification: All products starting with “k” are “king”, “kingdom”, and “kit”. The list remains the same for the ‘ki’ prefix.
  3. Example 3:
    • Input: Products: [“fantasy”, “fast”, “festival”], searchWord: “farm”
    • Expected Output: [[“fantasy”, “fast”, “festival”], [“fantasy”, “fast”], [], []]
    • Justification: Initially, “fantasy”, “fast”, and “festival” match ‘f’. Moving to ‘fa’, only “fantasy” and “fast” match. No product matches with “far”, and “farm”.

Constraints:

  • 1 <= products.length <= 1000
  • 1 <= products[i].length <= 3000
  • 1 <= sum(products[i].length) <= 2 * 10^4
  • All the strings of products are unique.
  • products[i] consists of lowercase English letters.
  • 1 <= searchWord.length <= 1000
  • searchWord consists of lowercase English letters.

Solution

To solve this problem, We will use the trie data structure to store the list of products. The trie is built by inserting each product, where each node represents a character. This structure allows us to efficiently find products that share a common prefix.

After building the trie, we process the search word by checking each of its prefixes. For each prefix, we perform a depth-first search (DFS) starting from the node matching the end of the prefix. The DFS is designed to find up to three lexicographically up to 3 smallest words that start with the given prefix. This approach of using a trie combined with DFS for each prefix ensures that we can quickly and effectively generate the required list of product suggestions.

Step-by-Step Algorithm

  1. Build the Trie:
    • Create a root node representing the starting point of the trie.
    • For each product:
      • Start from the root and for each character in the product, navigate to the corresponding child node. Create a new node if it doesn’t exist.
      • Mark the node corresponding to the last character of the product as a word end.
  2. Process Each Prefix of the Search Word:
    • Initialize an empty list to store the final suggestions for each prefix.
    • For each character in the search word, form a prefix.
      • Start from the root of the trie and navigate to the node corresponding to the last character of the current prefix.
      • If the node for the current prefix doesn’t exist, add an empty list to the suggestions and move to the next prefix.
  3. DFS for Each Prefix:
    • Upon reaching the node corresponding to the current prefix, perform a DFS.
      • Initialize an empty buffer to store up to three products.
      • Explore all possible paths from the current node. If a path leads to a node marked as a word end, add the corresponding product to the buffer.
      • Stop the DFS when you have collected three products or explored all paths.
  4. Compile Suggestions:
    • Add the buffer containing up to three products to the list of suggestions for the current prefix.
    • Continue the process for the next prefix.

Algorithm Walkthrough for Example 3

  • Input: Products = [“fantasy”, “fast”, “festival”], Search Word = “farm”
  • Walkthrough:
    1. Building the Trie:
      • Insert “fantasy”, “fast”, “festival” into the trie, creating nodes for each character.
      • Mark the end of each word in the trie.
    2. Processing Prefixes:
      • Prefix “f”: Node exists. Proceed to DFS.
      • Prefix “fa”: Node exists. Proceed to DFS.
      • Prefix “far”: Node does not exist. Add an empty list to suggestions and skip DFS.
      • Prefix “farm”: Node does not exist. Add an empty list to suggestions and skip DFS.
    3. DFS for “f” and “fa”:
      • For “f”: DFS finds “fantasy”, “fast”, “festival”. Add these to suggestions.
      • For “fa”: DFS finds “fantasy”, “fast”. Add these to suggestions.
    4. Final Output:
      • Suggestions: [[“fantasy”, “fast”, “festival”], [“fantasy”, “fast”], [], []].

This walkthrough illustrates how the trie efficiently organizes the products, and the DFS ensures that only the top three lexicographical matches for each prefix are selected.

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
# class TrieNode:
#     # Initialize a TrieNode with a dictionary to hold children nodes and a flag to mark word's end
#     def __init__(self):
#         self.children = {}
#         self.isEnd = False

class Trie:
    def __init__(self):
        self.root = TrieNode()

    def insert(self, word):
        node = self.root
        for ch in word:
            # Create a new child node if the character is not already a child of the current node
            if ch not in node.children:
                node.children[ch] = TrieNode()
            node = node.children[ch]
        # Mark the end of a word
        node.isEnd = True

    def dfs(self, node, prefix, list):
        # Stop if we already have 3 suggestions
        if len(list) == 3:
            return
        # Add the word to the list if we're at the end of a word
        if node.isEnd:
            list.append(prefix)

        # Recursively search for all possible words
        for ch in 'abcdefghijklmnopqrstuvwxyz':
            if ch in node.children:
                self.dfs(node.children[ch], prefix + ch, list)

    def search(self, prefix):
        node = self.root
        # Traverse the trie to the end of the prefix
        for ch in prefix:
            if ch not in node.children:
                return []  # Return an empty list if the prefix is not present
            node = node.children[ch]

        list = []
        self.dfs(node, prefix, list)  # Start DFS from the end of the current prefix
        return list


class Solution:
    def suggestedProducts(self, products, searchWord):
        trie = Trie()
        # Insert each product into the trie
        for product in products:
            trie.insert(product)

        result = []
        prefix = ''
        # For each character in the search word, find the top 3 suggestions
        for ch in searchWord:
            prefix += ch
            result.append(trie.search(prefix))
        return result


if __name__ == "__main__":
    solution = Solution()

    # Test Example 1
    products1 = ["apple", "apricot", "application"]
    searchWord1 = "app"
    print("Example 1:", solution.suggestedProducts(products1, searchWord1))

    # Test Example 2
    products2 = ["king", "kingdom", "kit"]
    searchWord2 = "ki"
    print("Example 2:", solution.suggestedProducts(products2, searchWord2))

    # Test Example 3
    products3 = ["fantasy", "fast", "festival"]
    searchWord3 = "farm"
    print("Example 3:", solution.suggestedProducts(products3, searchWord3))

Time and Space Complexity Analysis

Time Complexity

  • Building the Trie: (O(N x L)), where (N) is the number of products and (L) is the average length of the products.
  • Searching for Each Prefix: (O(M x K)), where (M) is the length of the search word and (K) is the time taken for the DFS, which is limited to 3 (constant time). Overall, it’s approximately (O(M)).

Overall Time Complexity: O(N * L + M), combining the time to build the Trie and perform searches.

Space Complexity

  • Trie Storage: (O(N x L)), as each product of average length (L) is stored in the trie.
  • Search Results: (O(M)), as we store up to 3 suggestions for each character in the search word.

Overall, the space complexity is dominated by the trie storage, which is (O(N x L)).

Author：Hasuer

Link：https://hasuer.github.io/23-pattern-trie/index.html

Publish date：May 23rd 2024, 2:24:12 pm

Update date：May 28th 2024, 11:30:41 am

License：本文采用知识共享署名-非商业性使用 4.0 国际许可协议进行许可

CATALOG
  1. 1. Introduction to Trie
    1. 1.1. Introduction to Trie
    2. 1.2. Defining a Trie
      1. 1.2.1. Need for Trie Data Structure?
      2. 1.2.2. Advantages of Using Tries
      3. 1.2.3. Properties of the Trie Data Structure
    3. 1.3. Implementation of Tries
      1. 1.3.1. Representation of Trie Node
      2. 1.3.2. Insertion in Trie Data Structure
        1. 1.3.2.1. Algorithm
        2. 1.3.2.2. Example
        3. 1.3.2.3. Code
        4. 1.3.2.4. Complexity Analysis
      3. 1.3.3. Searching in Trie Data Structure
        1. 1.3.3.1. Algorithm
        2. 1.3.3.2. Code
        3. 1.3.3.3. Complexity Analysis
      4. 1.3.4. Deletion in Trie Data Structure
        1. 1.3.4.1. Algorithm
        2. 1.3.4.2. Code
        3. 1.3.4.3. Complexity Analysis
  2. 2. Implement Trie (Prefix Tree)
    1. 2.1. Problem Statement
      1. 2.1.1. Examples
    2. 2.2. Solution
      1. 2.2.1. Algorithm Walkthrough
    3. 2.3. Code
    4. 2.4. Complexity Analysis
  3. 3. Index Pairs of a String
    1. 3.1. Problem Statement
      1. 3.1.1. Examples
    2. 3.2. Solution
      1. 3.2.1. Step-by-Step Algorithm
      2. 3.2.2. Algorithm Walkthrough
    3. 3.3. Code
    4. 3.4. Time and Space Complexity Analysis
  4. 4. Design Add and Search Words Data Structure
    1. 4.1. Problem Statement
      1. 4.1.1. Examples
    2. 4.2. Solution
      1. 4.2.1. Algorithm Walkthrough
    3. 4.3. Code
    4. 4.4. Complexity Analysis
  5. 5. # Extra Characters in a String
    1. 5.1. Problem Statement
      1. 5.1.1. Examples
    2. 5.2. Solution
      1. 5.2.1. Step-by-Step Algorithm
      2. 5.2.2. Algorithm Walkthrough
    3. 5.3. Code
    4. 5.4. Time and Space Complexity Analysis
      1. 5.4.1. Time Complexity
      2. 5.4.2. Space Complexity
  6. 6. Search Suggestions System
    1. 6.1. Problem Statement
      1. 6.1.1. Examples
    2. 6.2. Solution
      1. 6.2.1. Step-by-Step Algorithm
      2. 6.2.2. Algorithm Walkthrough for Example 3
    3. 6.3. Code
    4. 6.4. Time and Space Complexity Analysis
      1. 6.4.1. Time Complexity
      2. 6.4.2. Space Complexity
Total : 41
2024
2022
2021
Interview
技术笔记 Grokking-Interview-Pattern