Hasuer's Studio.

21. Pattern 01 Knapsack (Dynamic Programming)

Grokking Interview Pattern Interview
Word count: 8.5kReading time: 53 min
2024/05/21

Introduction

0/1 Knapsack pattern is based on the famous problem with the same name which is efficiently solved using Dynamic Programming (DP).

In this pattern, we will go through a set of problems to develop an understanding of DP. We will always start with a brute-force recursive solution to see the overlapping subproblems, i.e., realizing that we are solving the same problems repeatedly.

After the recursive solution, we will modify our algorithm to apply advanced techniques of Memoization and Bottom-Up Dynamic Programming to develop a complete understanding of this pattern.

Let’s jump onto our first problem.

*0/1 Knapsack (medium)

Design Gurus Educative.io

Introduction

Given the weights and profits of ‘N’ items, we are asked to put these items in a knapsack which has a capacity ‘C’. The goal is to get the maximum profit out of the items in the knapsack. Each item can only be selected once, as we don’t have multiple quantities of any item.

Let’s take the example of Merry, who wants to carry some fruits in the knapsack to get maximum profit. Here are the weights and profits of the fruits:

Items: { Apple, Orange, Banana, Melon }
Weights: { 2, 3, 1, 4 }
Profits: { 4, 5, 3, 7 }
Knapsack capacity: 5

Let’s try to put various combinations of fruits in the knapsack, such that their total weight is not more than 5:

Apple + Orange (total weight 5) => 9 profit
Apple + Banana (total weight 3) => 7 profit
Orange + Banana (total weight 4) => 8 profit
Banana + Melon (total weight 5) => 10 profit

This shows that Banana + Melon is the best combination as it gives us the maximum profit and the total weight does not exceed the capacity.

Problem Statement

Given two integer arrays to represent weights and profits of ‘N’ items, we need to find a subset of these items which will give us maximum profit such that their cumulative weight is not more than a given number ‘C’. Each item can only be selected once, which means either we put an item in the knapsack or we skip it.

Basic Solution

A basic brute-force solution could be to try all combinations of the given items (as we did above), allowing us to choose the one with maximum profit and a weight that doesn’t exceed ‘C’. Take the example of four items (A, B, C, and D), as shown in the diagram below. To try all the combinations, our algorithm will look like:

Here is a visual representation of our algorithm:

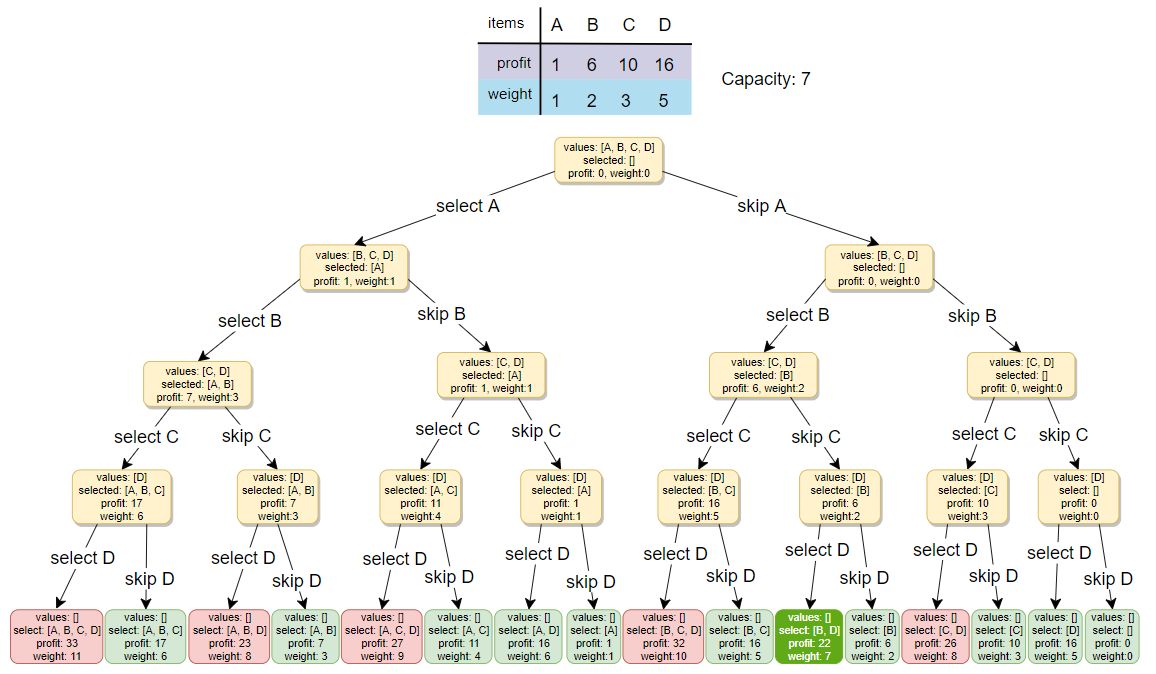
All green boxes have a total weight that is less than or equal to the capacity (7), and all the red ones have a weight that is more than 7. The best solution we have is with items [B, D] having a total profit of 22 and a total weight of 7.

Code

Here is the code for the brute-force solution:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution:
  def solveKnapsack(self, profits, weights, capacity):
    return self.knapsack_recursive(profits, weights, capacity, 0)


  def knapsack_recursive(self, profits, weights, capacity, currentIndex):
    # base checks
    if capacity <= 0 or currentIndex >= len(profits):
      return 0

    # recursive call after choosing the element at the currentIndex
    # if the weight of the element at currentIndex exceeds the capacity, we  shouldn't 
    # process this
    profit1 = 0
    if weights[currentIndex] <= capacity:
      profit1 = profits[currentIndex] + self.knapsack_recursive(
        profits, weights, capacity - weights[currentIndex], currentIndex + 1)

    # recursive call after excluding the element at the currentIndex
    profit2 = self.knapsack_recursive(profits, weights, capacity, currentIndex + 1)

    return max(profit1, profit2)


def main():
  sol = Solution()
  print(sol.solveKnapsack([1, 6, 10, 16], [1, 2, 3, 5], 7))
  print(sol.solveKnapsack([1, 6, 10, 16], [1, 2, 3, 5], 6))


main()

Time and Space complexity

The time complexity of the above algorithm is exponential O(2^n), where ‘n’ represents the total number of items. This can also be confirmed from the above recursion tree. As we can see, we will have a total of ‘31’ recursive calls – calculated through (2^n) + (2^n) - 1, which is asymptotically equivalent to O(2^n).

The space complexity is O(n). This space will be used to store the recursion stack. Since the recursive algorithm works in a depth-first fashion, which means that we can’t have more than ‘n’ recursive calls on the call stack at any time.

Overlapping Sub-problems: Let’s visually draw the recursive calls to see if there are any overlapping sub-problems. As we can see, in each recursive call, profits and weights arrays remain constant, and only capacity and currentIndex change. For simplicity, let’s denote capacity with ‘c’ and currentIndex with ‘i’:

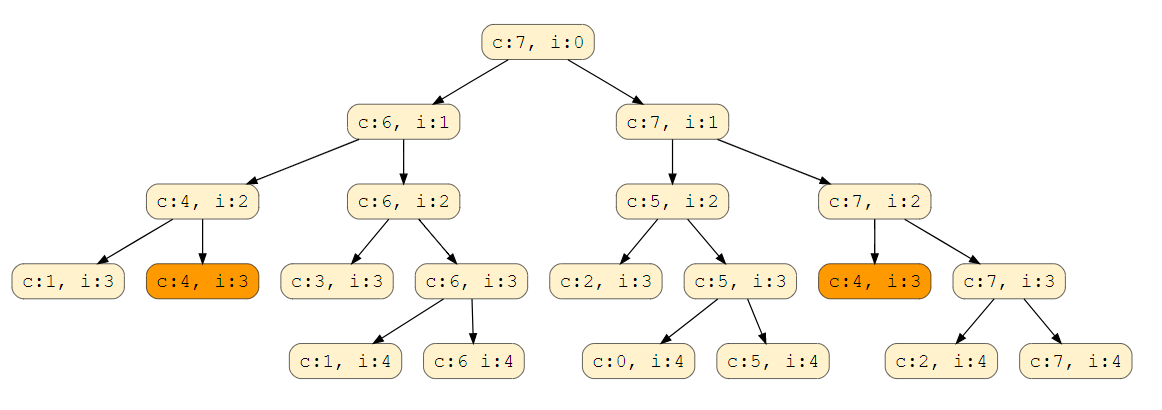
We can clearly see that ‘c:4, i=3’ has been called twice. Hence we have an overlapping sub-problems pattern. We can use Memoization to efficiently solve overlapping sub-problems.

Top-down Dynamic Programming with Memoization

Memoization is when we store the results of all the previously solved sub-problems and return the results from memory if we encounter a problem that has already been solved.

Since we have two changing values (capacity and currentIndex) in our recursive function knapsackRecursive(), we can use a two-dimensional array to store the results of all the solved sub-problems. As mentioned above, we need to store results for every sub-array (i.e. for every possible index ‘i’) and for every possible capacity ‘c’.

Code

Here is the code with memoization (see changes in the highlighted lines):

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
class Solution:
  def solveKnapsack(self, profits, weights, capacity):
    # create a two dimensional array for Memoization, each element is initialized to '-1'
    dp = [[-1 for x in range(capacity+1)] for y in range(len(profits))]
    return self.knapsack_recursive(dp, profits, weights, capacity, 0)


  def knapsack_recursive(self, dp, profits, weights, capacity, currentIndex):

    # base checks
    if capacity <= 0 or currentIndex >= len(profits):
      return 0

    # if we have already solved a similar problem, return the result from memory
    if dp[currentIndex][capacity] != -1:
      return dp[currentIndex][capacity]

    # recursive call after choosing the element at the currentIndex
    # if the weight of the element at currentIndex exceeds the capacity, we
    # shouldn't process this
    profit1 = 0
    if weights[currentIndex] <= capacity:
      profit1 = profits[currentIndex] + self.knapsack_recursive(
        dp, profits, weights, capacity - weights[currentIndex], currentIndex + 1)

    # recursive call after excluding the element at the currentIndex
    profit2 = self.knapsack_recursive(
      dp, profits, weights, capacity, currentIndex + 1)

    dp[currentIndex][capacity] = max(profit1, profit2)
    return dp[currentIndex][capacity]



def main():
  sol = Solution()
  print(sol.solveKnapsack([1, 6, 10, 16], [1, 2, 3, 5], 7))
  print(sol.solveKnapsack([1, 6, 10, 16], [1, 2, 3, 5], 6))


main()

Time and Space complexity

Since our memoization array dp[profits.length][capacity+1] stores the results for all subproblems, we can conclude that we will not have more than N*C subproblems (where ‘N’ is the number of items and ‘C’ is the knapsack capacity). This means that our time complexity will be O(N\C)*.

The above algorithm will use O(N\C)* space for the memoization array. Other than that we will use O(N) space for the recursion call-stack. So the total space complexity will be O(N\C + N)*, which is asymptotically equivalent to O(N\C)*.

Bottom-up Dynamic Programming

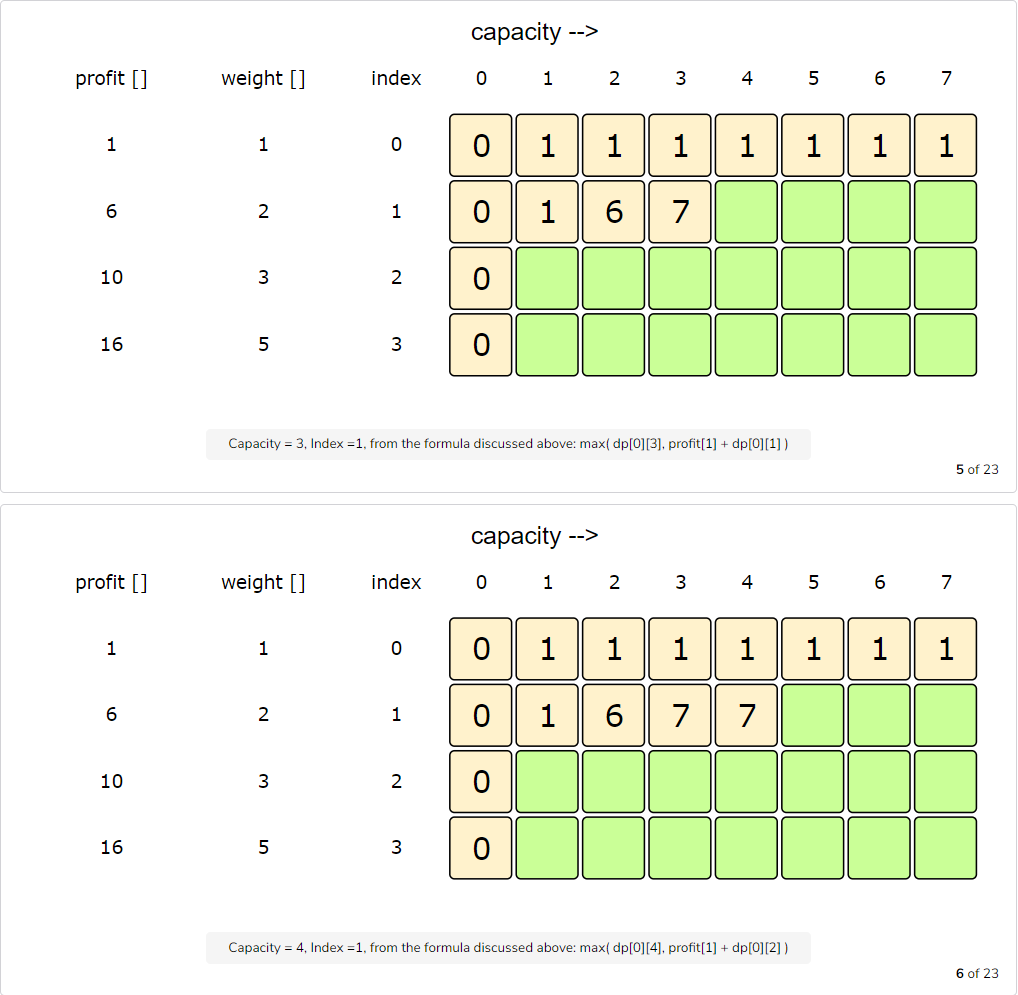
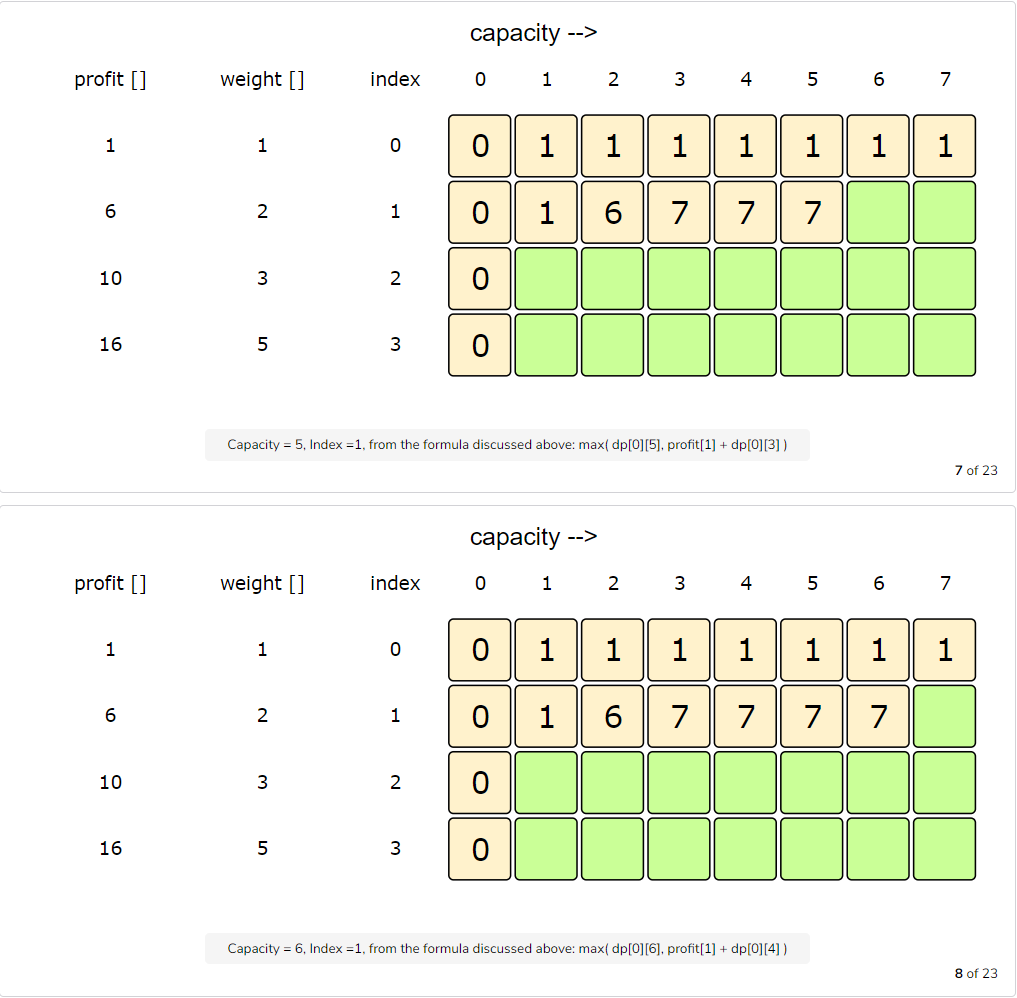
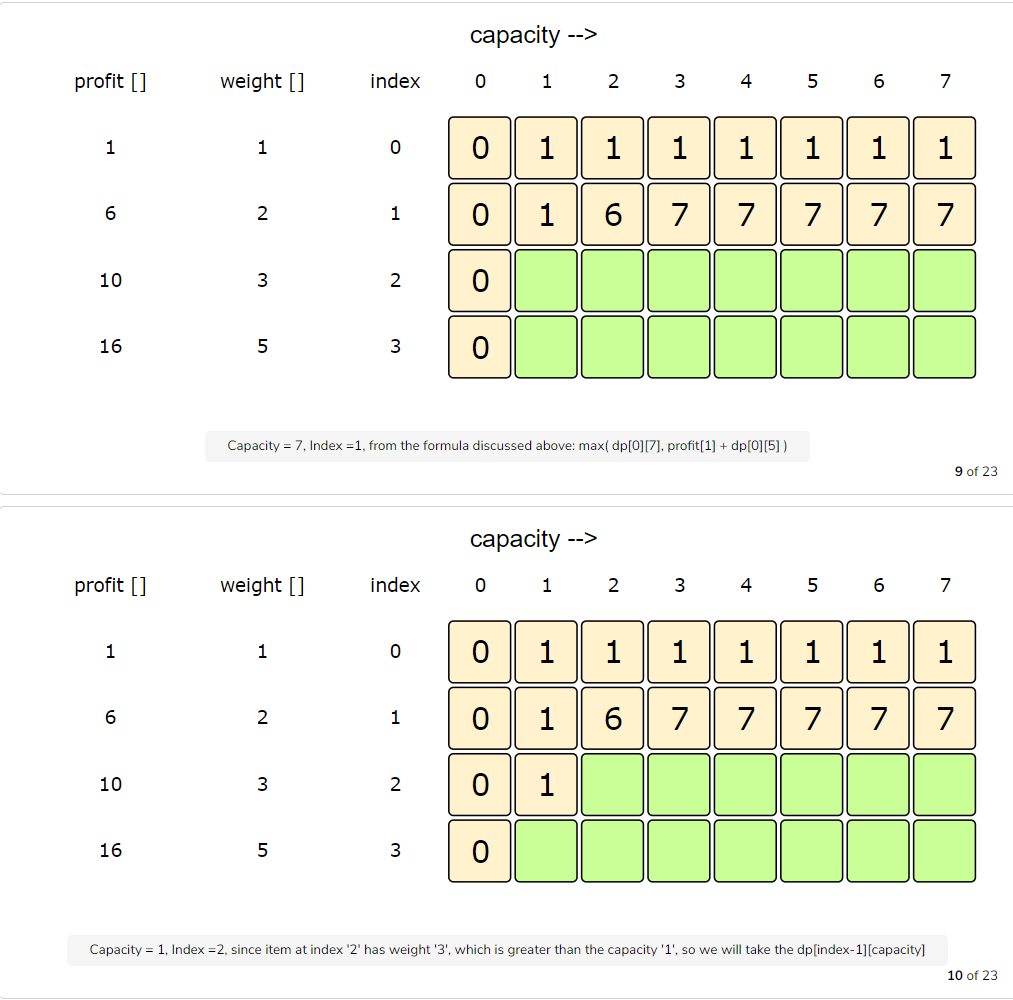
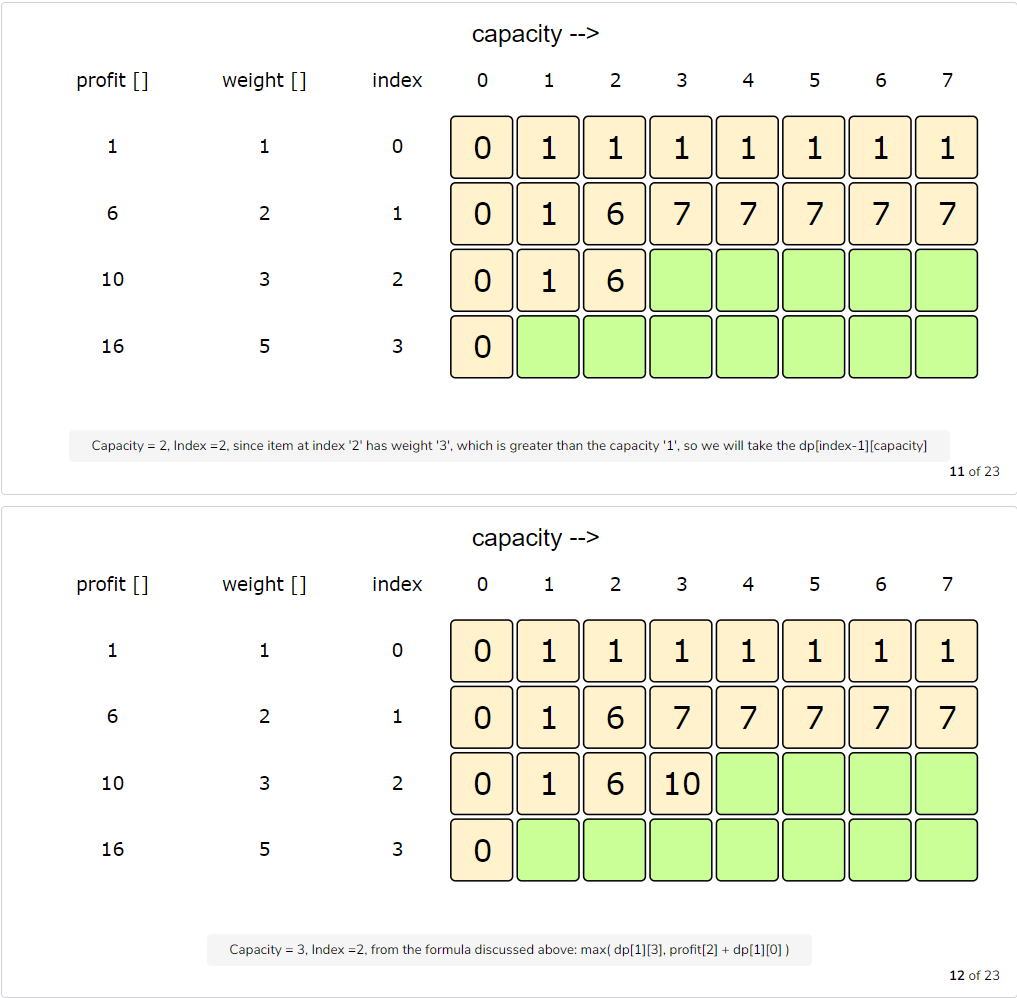
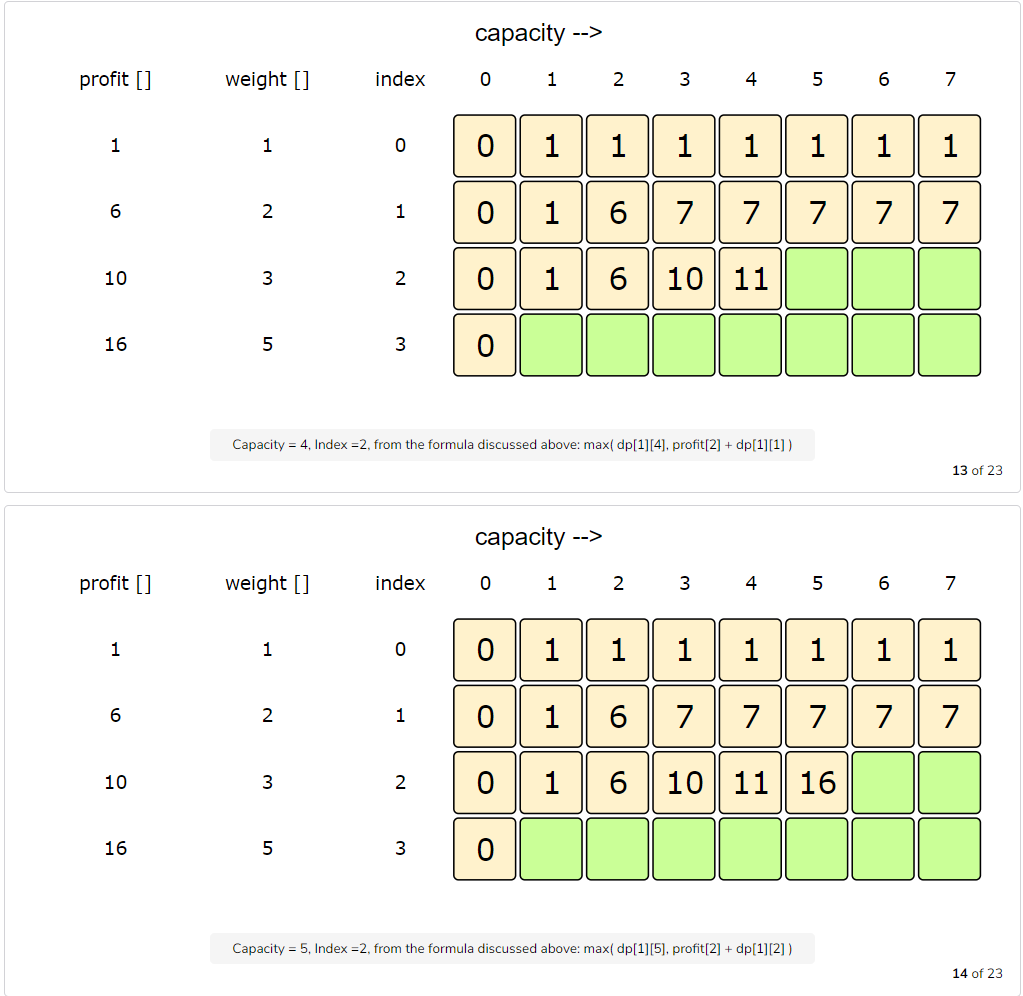
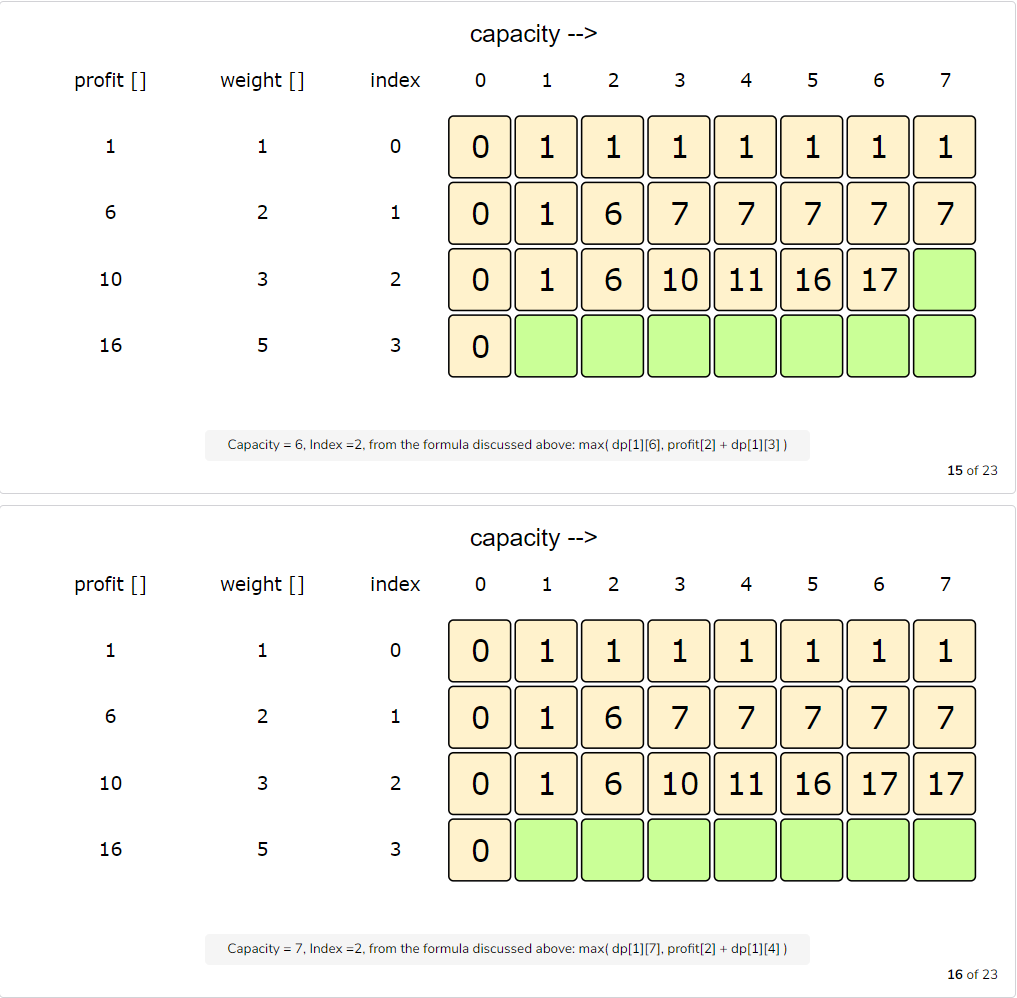
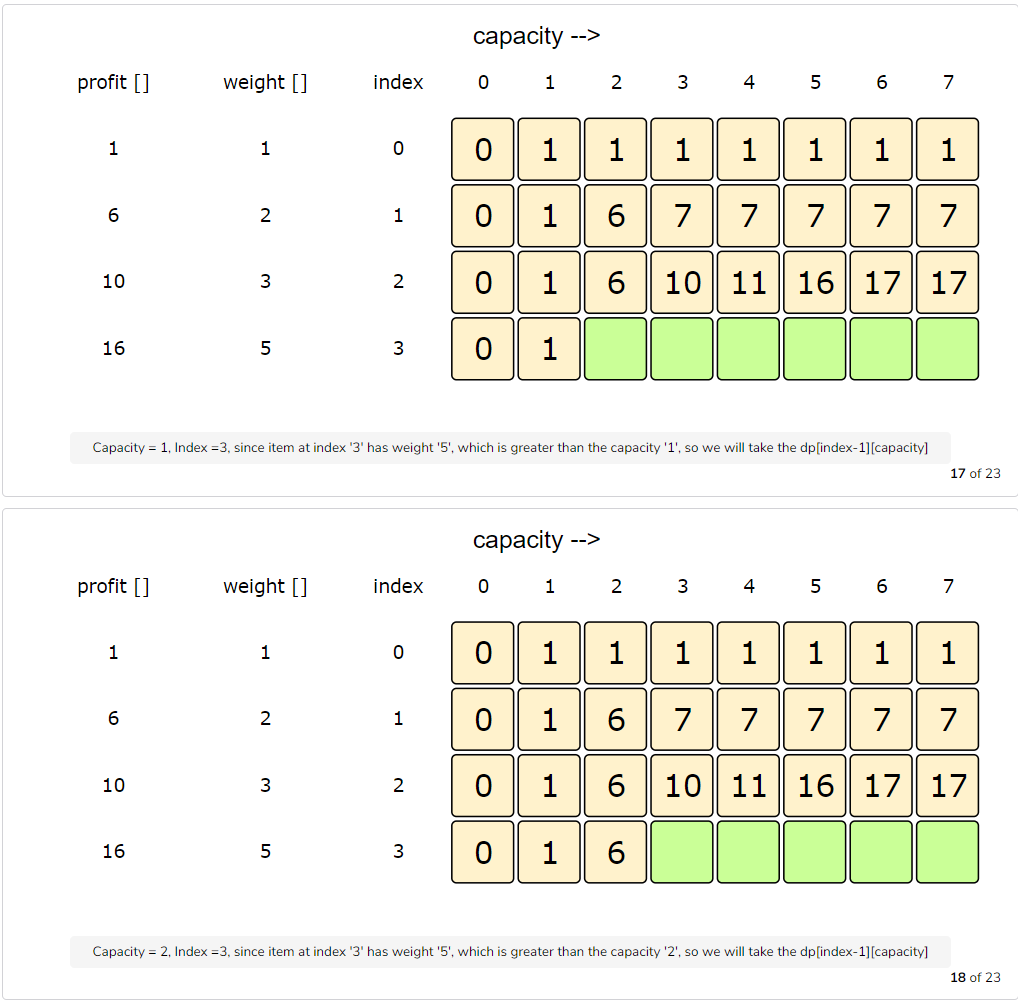
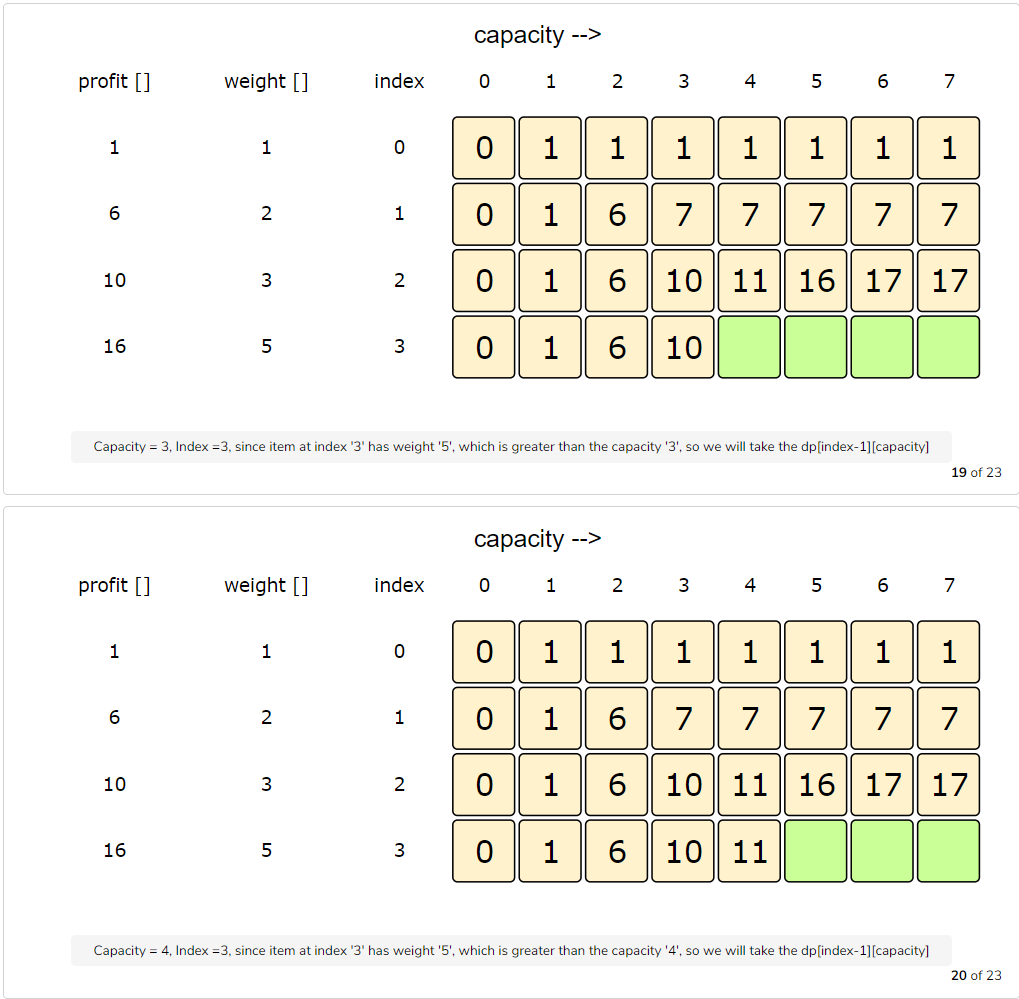
Let’s try to populate our dp[][] array from the above solution by working in a bottom-up fashion. Essentially, we want to find the maximum profit for every sub-array and for every possible capacity. This means that dp[i][c] will represent the maximum knapsack profit for capacity ‘c’ calculated from the first ‘i’ items.

So, for each item at index ‘i’ (0 <= i < items.length) and capacity ‘c’ (0 <= c <= capacity), we have two options:

  1. Exclude the item at index ‘i’. In this case, we will take whatever profit we get from the sub-array excluding this item => dp[i-1][c]
  2. Include the item at index ‘i’ if its weight is not more than the capacity. In this case, we include its profit plus whatever profit we get from the remaining capacity and from remaining items => profit[i] + dp[i-1][c-weight[i]]

Finally, our optimal solution will be maximum of the above two values:

1
dp[i][c] = max (dp[i-1][c], profit[i] + dp[i-1][c-weight[i]])

Let’s draw this visually and start with our base case of zero capacity:

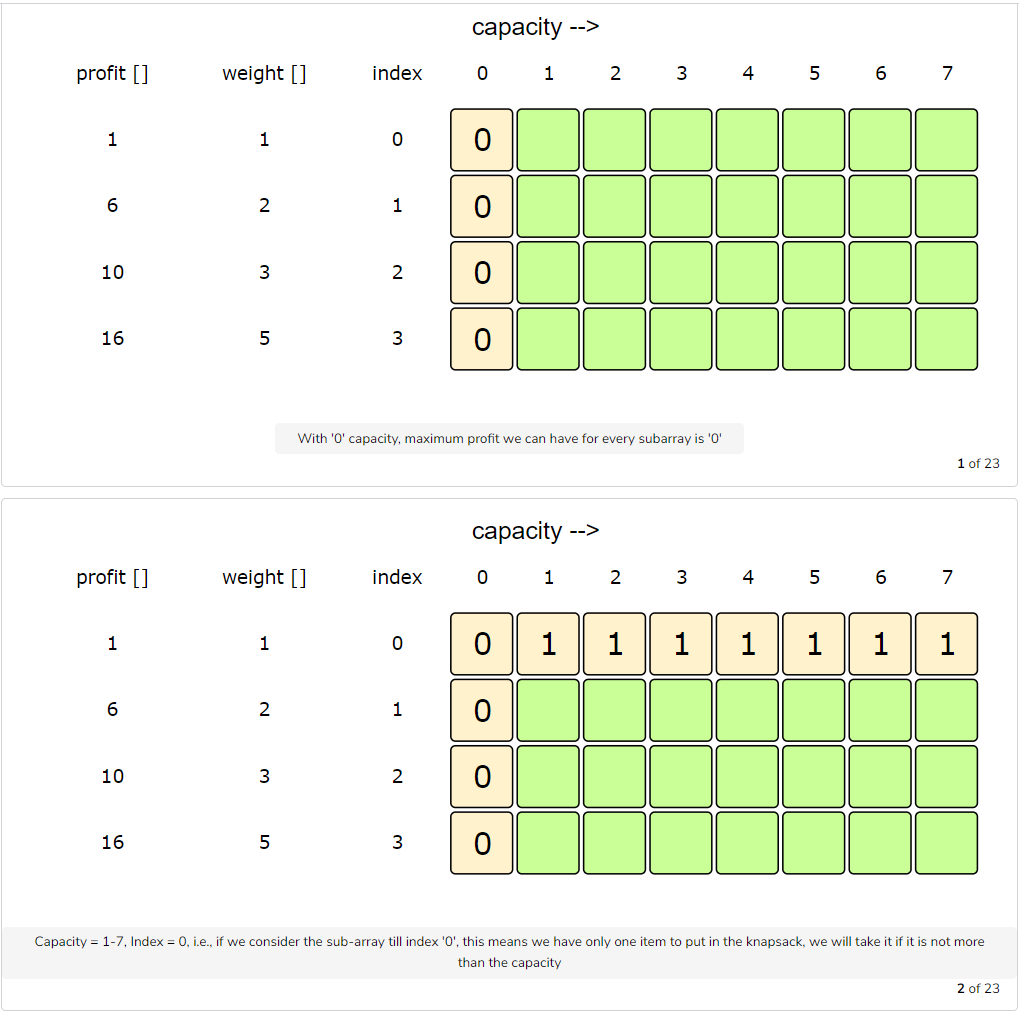
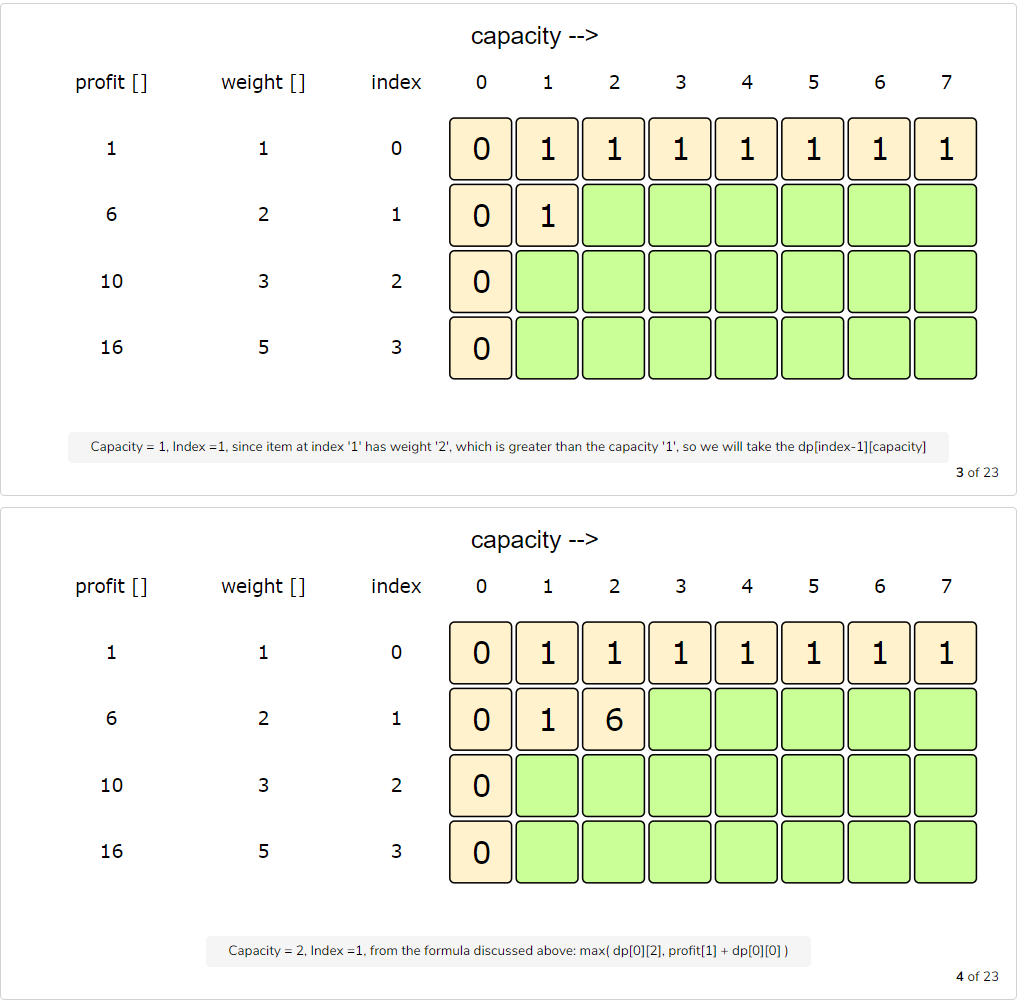
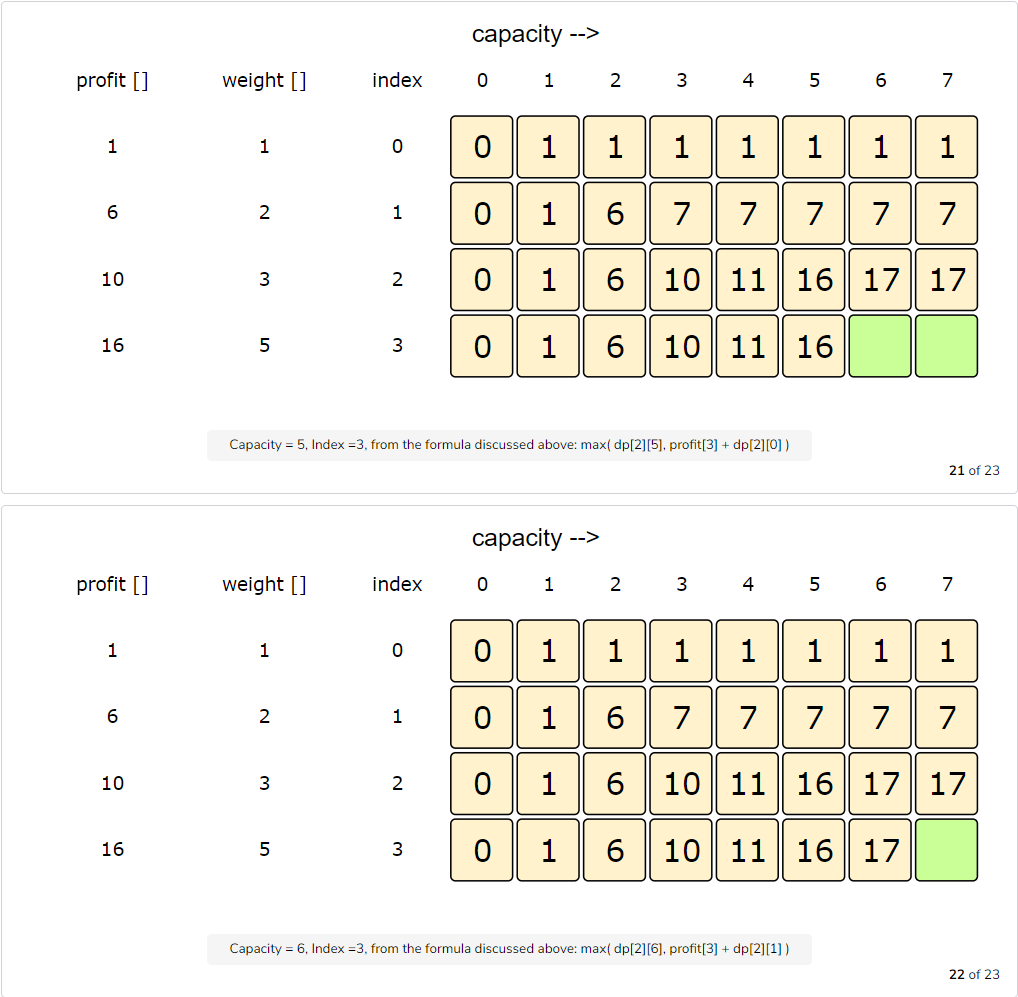
Code

Here is the code for our bottom-up dynamic programming approach:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
class Solution:
  def solveKnapsack(self, profits, weights, capacity):
    # basic checks
    n = len(profits)
    if capacity <= 0 or n == 0 or len(weights) != n:
      return 0

    dp = [[0 for x in range(capacity+1)] for y in range(n)]

    # populate the capacity = 0 columns, with '0' capacity we have '0' profit
    for i in range(0, n):
      dp[i][0] = 0

    # if we have only one weight, we will take it if it is not more than the capacity
    for c in range(0, capacity+1):
      if weights[0] <= c:
        dp[0][c] = profits[0]

    # process all sub-arrays for all the capacities
    for i in range(1, n):
      for c in range(1, capacity+1):
        profit1, profit2 = 0, 0
        # include the item, if it is not more than the capacity
        if weights[i] <= c:
          profit1 = profits[i] + dp[i - 1][c - weights[i]]
        # exclude the item
        profit2 = dp[i - 1][c]
        # take maximum
        dp[i][c] = max(profit1, profit2)

    # maximum profit will be at the bottom-right corner.
    return dp[n - 1][capacity]


def main():
  sol = Solution()
  print(sol.solveKnapsack([1, 6, 10, 16], [1, 2, 3, 5], 5))
  print(sol.solveKnapsack([1, 6, 10, 16], [1, 2, 3, 5], 6))
  print(sol.solveKnapsack([1, 6, 10, 16], [1, 2, 3, 5], 7))


main()

Time and Space complexity

The above solution has the time and space complexity of O(N\C)*, where ‘N’ represents total items and ‘C’ is the maximum capacity.

How can we find the selected items?

As we know, the final profit is at the bottom-right corner. Therefore, we will start from there to find the items that will be going into the knapsack.

As you remember, at every step we had two options: include an item or skip it. If we skip an item, we take the profit from the remaining items (i.e. from the cell right above it); if we include the item, then we jump to the remaining profit to find more items.

Let’s understand this from the above example:

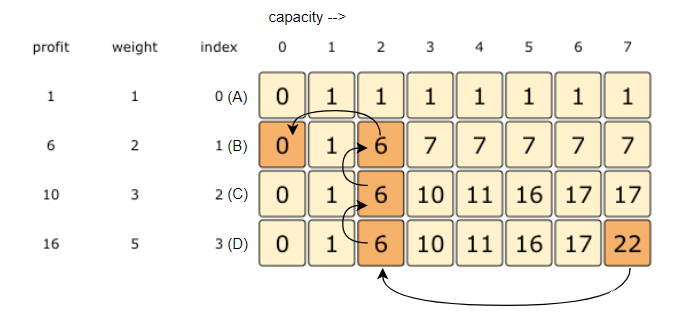
  1. ‘22’ did not come from the top cell (which is 17); hence we must include the item at index ‘3’ (which is item ‘D’).
  2. Subtract the profit of item ‘D’ from ‘22’ to get the remaining profit ‘6’. We then jump to profit ‘6’ on the same row.
  3. ‘6’ came from the top cell, so we jump to row ‘2’.
  4. Again ‘6’ came from the top cell, so we jump to row ‘1’.
  5. ‘6’ is different than the top cell, so we must include this item (which is item ‘B’).
  6. Subtract the profit of ‘B’ from ‘6’ to get profit ‘0’. We then jump to profit ‘0’ on the same row. As soon as we hit zero remaining profit, we can finish our item search.
  7. Thus the items going into the knapsack are {B, D}.

Let’s write a function to print the set of items included in the knapsack.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
class Solution:
  def solveKnapsack(self, profits, weights, capacity):
    # basic checks
    n = len(profits)
    if capacity <= 0 or n == 0 or len(weights) != n:
      return 0

    dp = [[0 for x in range(capacity+1)] for y in range(n)]

    # populate the capacity = 0 columns, with '0' capacity we have '0' profit
    for i in range(0, n):
      dp[i][0] = 0

    # if we have only one weight, we will take it if it is not more than the capacity
    for c in range(0, capacity+1):
      if weights[0] <= c:
        dp[0][c] = profits[0]

    # process all sub-arrays for all the capacities
    for i in range(1, n):
      for c in range(1, capacity+1):
        profit1, profit2 = 0, 0
        # include the item, if it is not more than the capacity
        if weights[i] <= c:
          profit1 = profits[i] + dp[i - 1][c - weights[i]]
        # exclude the item
        profit2 = dp[i - 1][c]
        # take maximum
        dp[i][c] = max(profit1, profit2)

    self.print_selected_elements(dp, weights, profits, capacity)
    # maximum profit will be at the bottom-right corner.
    return dp[n - 1][capacity]


  def print_selected_elements(self, dp, weights, profits, capacity):
    print("Selected weights are: ", end='')
    n = len(weights)
    totalProfit = dp[n-1][capacity]
    for i in range(n-1, 0, -1):
      if totalProfit != dp[i - 1][capacity]:
        print(str(weights[i]) + " ", end='')
        capacity -= weights[i]
        totalProfit -= profits[i]

    if totalProfit != 0:
      print(str(weights[0]) + " ", end='')
    print()


def main():
  sol = Solution()
  print("Total knapsack profit: " +
        str(sol.solveKnapsack([1, 6, 10, 16], [1, 2, 3, 5], 7)))
  print("Total knapsack profit: " +
        str(sol.solveKnapsack([1, 6, 10, 16], [1, 2, 3, 5], 6)))


main()

Challenge

Can we further improve our bottom-up DP solution? Can you find an algorithm that has space complexity?

We only need one previous row to find the optimal solution!

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
class Solution:
    def solveKnapsack(self, profits, weights, capacity):
        # basic checks
        n = len(profits)
        if capacity <= 0 or n == 0 or len(weights) != n:
            return 0

        # we only need one previous row to find the optimal solution, overall we need '2' rows
        # the above solution is similar to the previous solution, the only difference is that
        # we use `i % 2` instead if `i` and `(i-1) % 2` instead if `i-1`
        # 注意这里初始化都是0，不然就要单独初始化第一列
        dp = [[0 for x in range(capacity + 1)] for y in range(2)]

        # if we have only one weight, we will take it if it is not more than the capacity
        for c in range(0, capacity + 1):
            if weights[0] <= c:
                dp[0][c] = dp[1][c] = profits[0]

        # process all sub-arrays for all the capacities
        for i in range(1, n):
            for c in range(0, capacity + 1):
                profit1, profit2 = 0, 0
                # include the item, if it is not more than the capacity
                if weights[i] <= c:
                    profit1 = profits[i] + dp[(i - 1) % 2][c - weights[i]]
                # exclude the item
                profit2 = dp[(i - 1) % 2][c]
                # take maximum
                dp[i % 2][c] = max(profit1, profit2)

        return dp[(n - 1) % 2][capacity]


def main():
    sol = Solution()
    print("Total knapsack profit: " +
          str(sol.solveKnapsack([1, 6, 10, 16], [1, 2, 3, 5], 7)))
    print("Total knapsack profit: " +
          str(sol.solveKnapsack([1, 6, 10, 16], [1, 2, 3, 5], 6)))


main()

The solution above is similar to the previous solution, the only difference is that we use i%2 instead if i and (i-1)%2 instead if i-1. This solution has a space complexity of O(2\C) = O(C)*, where ‘C’ is the maximum capacity of the knapsack.

This space optimization solution can also be implemented using a single array. It is a bit tricky, but the intuition is to use the same array for the previous and the next iteration!

If you see closely, we need two values from the previous iteration: dp[c] and dp[c-weight[i]]

Since our inner loop is iterating over c:0-->capacity, let’s see how this might affect our two required values:

  1. When we access dp[c], it has not been overridden yet for the current iteration, so it should be fine.
  2. dp[c-weight[i]] might be overridden if “weight[i] > 0”. Therefore we can’t use this value for the current iteration.

To solve the second case, we can change our inner loop to process in the reverse direction: c:capacity-->0. This will ensure that whenever we change a value in dp[], we will not need it again in the current iteration.

Can you try writing this algorithm?

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
class Solution:
  def solveKnapsack(self, profits, weights, capacity):
    # basic checks
    n = len(profits)
    if capacity <= 0 or n == 0 or len(weights) != n:
      return 0

    dp = [0 for x in range(capacity+1)]

    # if we have only one weight, we will take it if it is not more than the capacity
    for c in range(0, capacity+1):
      if weights[0] <= c:
        dp[c] = profits[0]

    # process all sub-arrays for all the capacities
    for i in range(1, n):
      for c in range(capacity, -1, -1):
        profit1, profit2 = 0, 0
        # include the item, if it is not more than the capacity
        if weights[i] <= c:
          profit1 = profits[i] + dp[c - weights[i]]
        # exclude the item
        profit2 = dp[c]
        # take maximum
        dp[c] = max(profit1, profit2)

    return dp[capacity]


def main():
  sol = Solution()
  print("Total knapsack profit: " +
        str(sol.solveKnapsack([1, 6, 10, 16], [1, 2, 3, 5], 7)))
  print("Total knapsack profit: " +
        str(sol.solveKnapsack([1, 6, 10, 16], [1, 2, 3, 5], 6)))


main()

Equal Subset Sum Partition (medium)

416. Partition Equal Subset Sum Design Gurus Educative.io

Problem Statement

Given a set of positive numbers, find if we can partition it into two subsets such that the sum of elements in both subsets is equal.

Example 1:

1
2
3
Input: {1, 2, 3, 4}
Output: True
Explanation: The given set can be partitioned into two subsets with equal sum: {1, 4} & {2, 3}

Example 2:

1
2
3
Input: {1, 1, 3, 4, 7}
Output: True
Explanation: The given set can be partitioned into two subsets with equal sum: {1, 3, 4} & {1, 7}

Example 3:

1
2
3
Input: {2, 3, 4, 6}
Output: False
Explanation: The given set cannot be partitioned into two subsets with equal sum.

Constraints:

  • 1 <= nums.length <= 200
  • 1 <= nums[i] <= 100

Basic Solution

This problem follows the 0/1 Knapsack pattern. A basic brute-force solution could be to try all combinations of partitioning the given numbers into two sets to see if any pair of sets has an equal sum.

Assume that S represents the total sum of all the given numbers. Then the two equal subsets must have a sum equal to S/2. This essentially transforms our problem to: “Find a subset of the given numbers that has a total sum of S/2“.

So our brute-force algorithm will look like:

Code

Here is the code for the brute-force solution:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
class Solution:
  def canPartition(self, num):
    s = sum(num)
    # if 's' is a an odd number, we can't have two subsets with equal sum
    if s % 2 != 0:
      return False

    return self.can_partition_recursive(num, s / 2, 0)


  def can_partition_recursive(self, num, sum, currentIndex):
    # base check
    if sum == 0:
      return True

    n = len(num)
    if n == 0 or currentIndex >= n:
      return False

    # recursive call after choosing the number at the `currentIndex`
    # if the number at `currentIndex` exceeds the sum, we shouldn't process this
    if num[currentIndex] <= sum:
      if(self.can_partition_recursive(num, sum - num[currentIndex], currentIndex + 1)):
        return True

    # recursive call after excluding the number at the 'currentIndex'
    return self.can_partition_recursive(num, sum, currentIndex + 1)


def main():
  sol = Solution()
  print("Can partition: " + str(sol.canPartition([1, 2, 3, 4])))
  print("Can partition: " + str(sol.canPartition([1, 1, 3, 4, 7])))
  print("Can partition: " + str(sol.canPartition([2, 3, 4, 6])))


main()

Time and Space complexity

The time complexity of the above algorithm is exponential O(2^n), where ‘n’ represents the total number. The space complexity is O(n), which will be used to store the recursion stack.

Top-down Dynamic Programming with Memoization

We can use memoization to overcome the overlapping sub-problems. As stated in previous lessons, memoization is when we store the results of all the previously solved sub-problems so we can return the results from memory if we encounter a problem that has already been solved.

Since we need to store the results for every subset and for every possible sum, therefore we will be using a two-dimensional array to store the results of the solved sub-problems. The first dimension of the array will represent different subsets and the second dimension will represent different ‘sums’ that we can calculate from each subset. These two dimensions of the array can also be inferred from the two changing values (sum and currentIndex) in our recursive function canPartitionRecursive().

Code

Here is the code for Top-down DP with memoization:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
class Solution:
    def canPartition(self, num):
        s = sum(num)

        # if 's' is a an odd number, we can't have two subsets with equal sum
        if s % 2 != 0:
            return False
        # 这里需要注意是s/2+1,需要+1
        # initialize the 'dp' array, -1 for default, 1 for true and 0 for false
        dp = [[-1 for x in range(int(s / 2) + 1)] for y in range(len(num))]
        return True if self.can_partition_recursive(dp, num, int(s / 2), 0) == 1 else False

    def can_partition_recursive(self, dp, num, sum, currentIndex):
        # base check
        if sum == 0:
            return 1

        n = len(num)
        if n == 0 or currentIndex >= n:
            return 0

        # if we have not already processed a similar problem
        if dp[currentIndex][sum] == -1:
            # recursive call after choosing the number at the currentIndex
            # if the number at currentIndex exceeds the sum, we shouldn't process this
            if num[currentIndex] <= sum:
                if self.can_partition_recursive(dp, num, sum - num[currentIndex], currentIndex + 1) \
                        == 1:
                    dp[currentIndex][sum] = 1
                    return 1

            # recursive call after excluding the number at the currentIndex
            dp[currentIndex][sum] = self.can_partition_recursive(
                dp, num, sum, currentIndex + 1)

        return dp[currentIndex][sum]


def main():
    sol = Solution()
    print("Can partition: " + str(sol.canPartition([1, 2, 3, 4])))
    print("Can partition: " + str(sol.canPartition([1, 1, 3, 4, 7])))
    print("Can partition: " + str(sol.canPartition([2, 3, 4, 6])))


main()

Time and Space complexity

The above algorithm has the time and space complexity of O(N\S)*, where ‘N’ represents total numbers and ‘S’ is the total sum of all the numbers.

Bottom-up Dynamic Programming

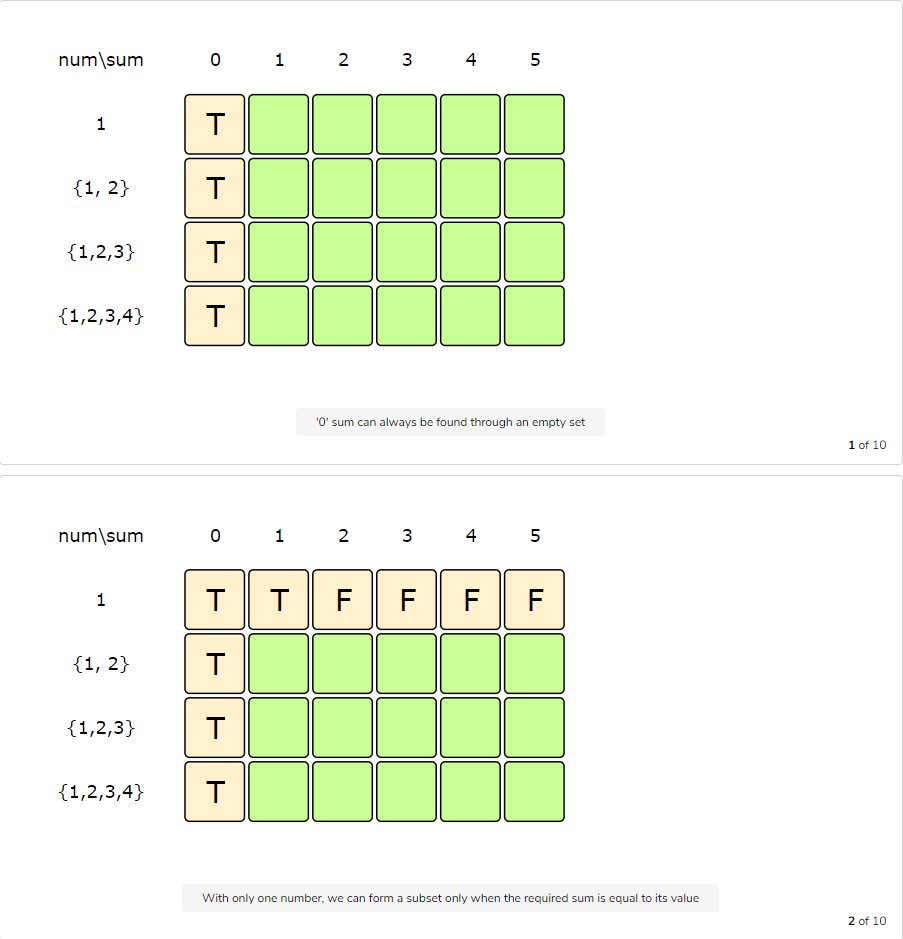
Let’s try to populate our dp[][] array from the above solution by working in a bottom-up fashion. Essentially, we want to find if we can make all possible sums with every subset. This means, dp[i][s] will be ‘true’ if we can make the sum ‘s’ from the first ‘i’ numbers.

So, for each number at index ‘i’ (0 <= i < num.length) and sum ‘s’ (0 <= s <= S/2), we have two options:

  1. Exclude the number. In this case, we will see if we can get ‘s’ from the subset excluding this number: dp[i-1][s]
  2. Include the number if its value is not more than ‘s’. In this case, we will see if we can find a subset to get the remaining sum: dp[i-1][s-num[i]]

If either of the two above scenarios is true, we can find a subset of numbers with a sum equal to ‘s’.

Let’s start with our base case of zero capacity:

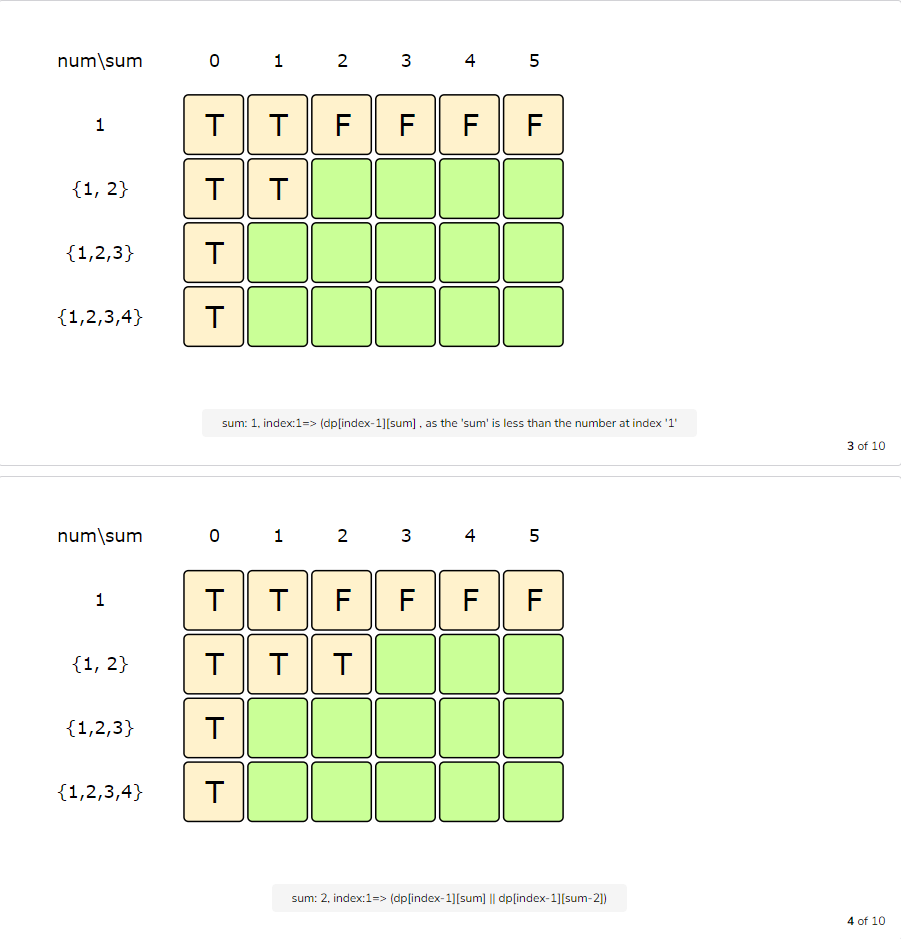
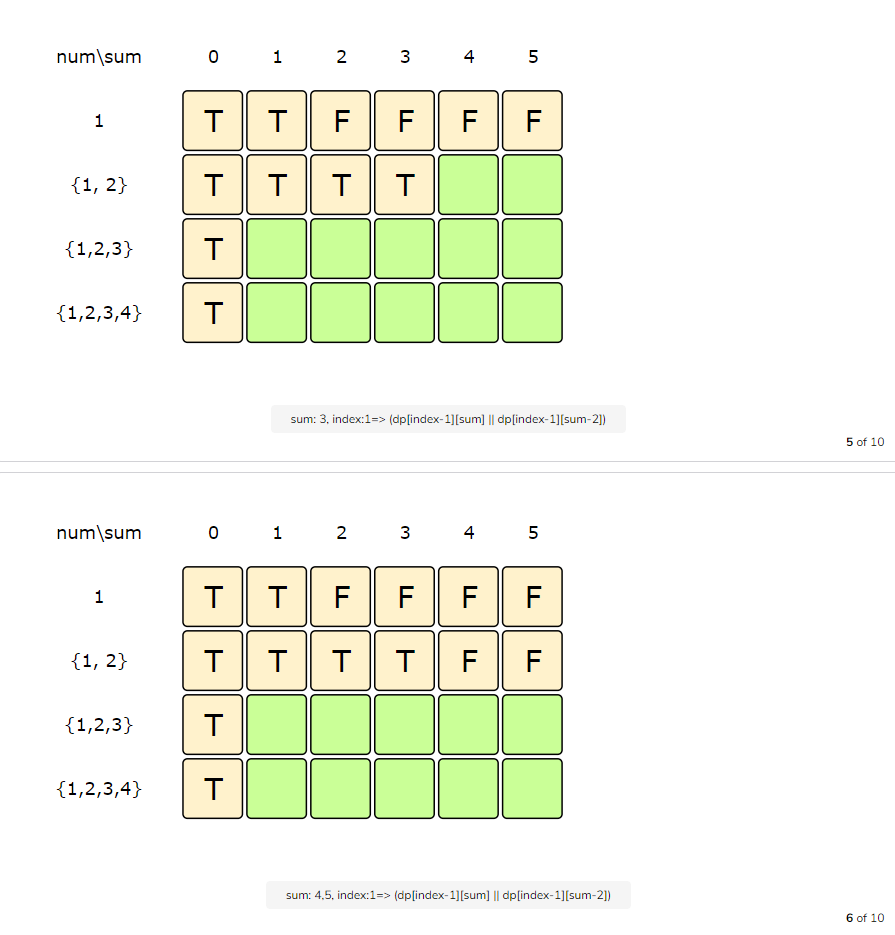
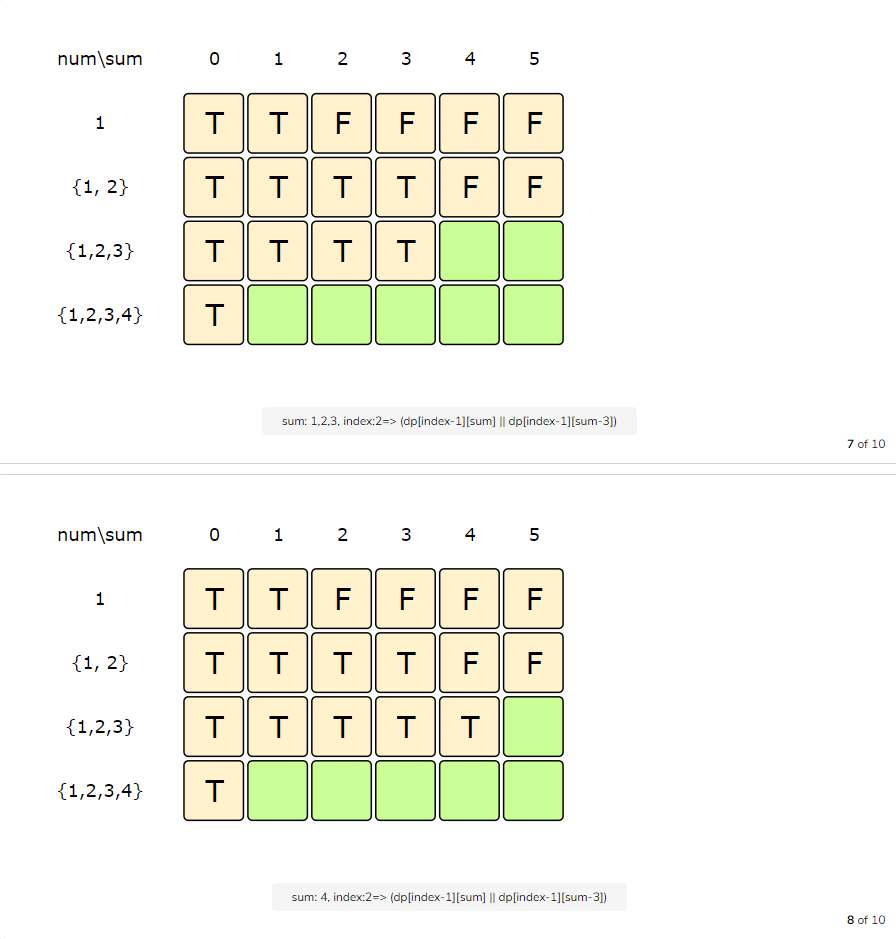
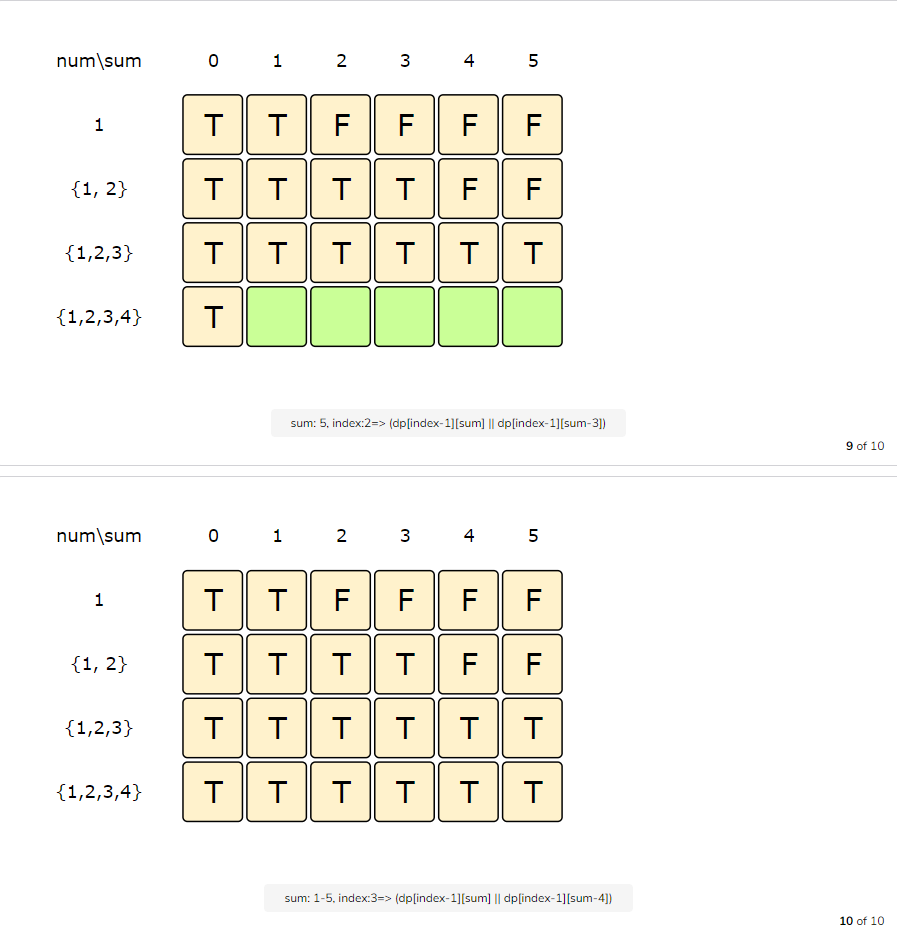
From the above visualization, we can clearly see that it is possible to partition the given set into two subsets with equal sums, as shown by bottom-right cell: dp[3][5] => T

Code

Here is the code for our bottom-up dynamic programming approach:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
class Solution:
    def canPartition(self, num):
        s = sum(num)

        # if 's' is a an odd number, we can't have two subsets with same total
        if s % 2 != 0:
            return False

        # we are trying to find a subset of given numbers that has a total sum of 's/2'.
        s = int(s / 2)

        n = len(num)
        # 这里需要注意是s/2+1,需要+1
        dp = [[False for x in range(s + 1)] for y in range(n)]

        # populate the s=0 columns, as we can always for '0' sum with an empty set
        for i in range(0, n):
            dp[i][0] = True

        # with only one number, we can form a subset only when the required sum is
        # equal to its value
        for j in range(1, s + 1):
            dp[0][j] = num[0] == j

        # process all subsets for all sums
        for i in range(1, n):
            for j in range(1, s + 1):
                # if we can get the sum 'j' without the number at index 'i'
                if dp[i - 1][j]:
                    dp[i][j] = dp[i - 1][j]
                elif j >= num[i]:  # else if we can find a subset to get the remaining sum
                    dp[i][j] = dp[i - 1][j - num[i]]

        # the bottom-right corner will have our answer.
        return dp[n - 1][s]


def main():
    sol = Solution()
    print("Can partition: " + str(sol.canPartition([1, 2, 3, 4])))
    print("Can partition: " + str(sol.canPartition([1, 1, 3, 4, 7])))
    print("Can partition: " + str(sol.canPartition([2, 3, 4, 6])))


main()

Time and Space complexity

The above solution the has time and space complexity of O(N\S)*, where ‘N’ represents total numbers and ‘S’ is the total sum of all the numbers.

Subset Sum (medium)

Similar | 416. Partition Equal Subset Sum Design Gurus Educative.io

Problem Statement

Given a set of positive numbers, determine if a subset exists whose sum is equal to a given number ‘S’.

Example 1:

1
2
3
Input: {1, 2, 3, 7}, S=6
Output: True
The given set has a subset whose sum is '6': {1, 2, 3}

Example 2:

1
2
3
Input: {1, 2, 7, 1, 5}, S=10
Output: True
The given set has a subset whose sum is '10': {1, 2, 7}

Example 3:

1
2
3
Input: {1, 3, 4, 8}, S=6
Output: False
The given set does not have any subset whose sum is equal to '6'.

Constraints:

  • 1 <= num.length <= 200
  • 1 <= num[i] <= 100

Basic Solution

This problem follows the 0/1 Knapsack pattern and is quite similar to Equal Subset Sum Partition. A basic brute-force solution could be to try all subsets of the given numbers to see if any set has a sum equal to ‘S’.

So our brute-force algorithm will look like:

Since this problem is quite similar to Equal Subset Sum Partition, let’s jump directly to the bottom-up dynamic programming solution.

Bottom-up Dynamic Programming

We’ll try to find if we can make all possible sums with every subset to populate the array dp[TotalNumbers][S+1].

For every possible sum ‘s’ (where 0 <= s <= S), we have two options:

  1. Exclude the number. In this case, we will see if we can get the sum ‘s’ from the subset excluding this number => dp[index-1][s]
  2. Include the number if its value is not more than ‘s’. In this case, we will see if we can find a subset to get the remaining sum => dp[index-1][s-num[index]]

If either of the above two scenarios returns true, we can find a subset with a sum equal to ‘s’.

Let’s draw this visually, with the example input {1, 2, 3, 7}, and start with our base case of size zero:

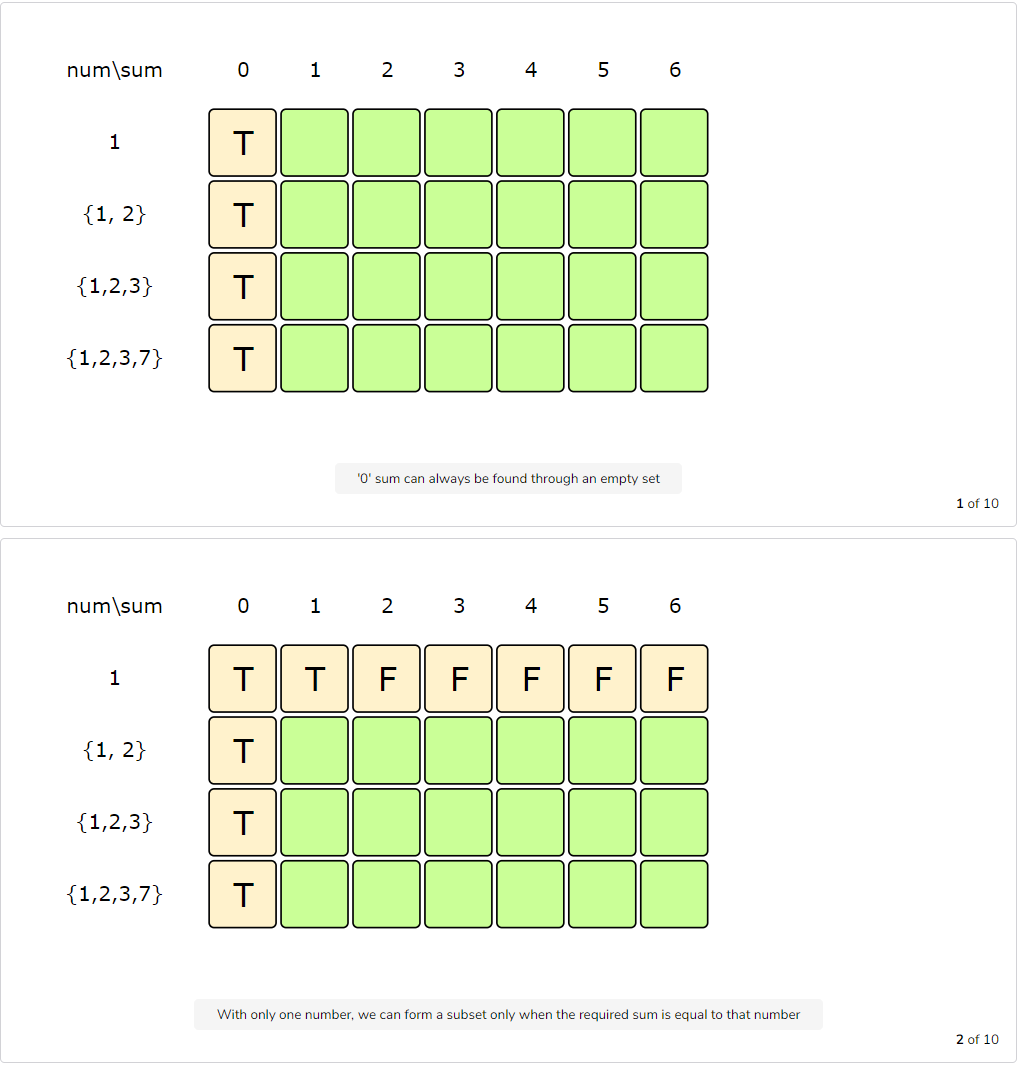
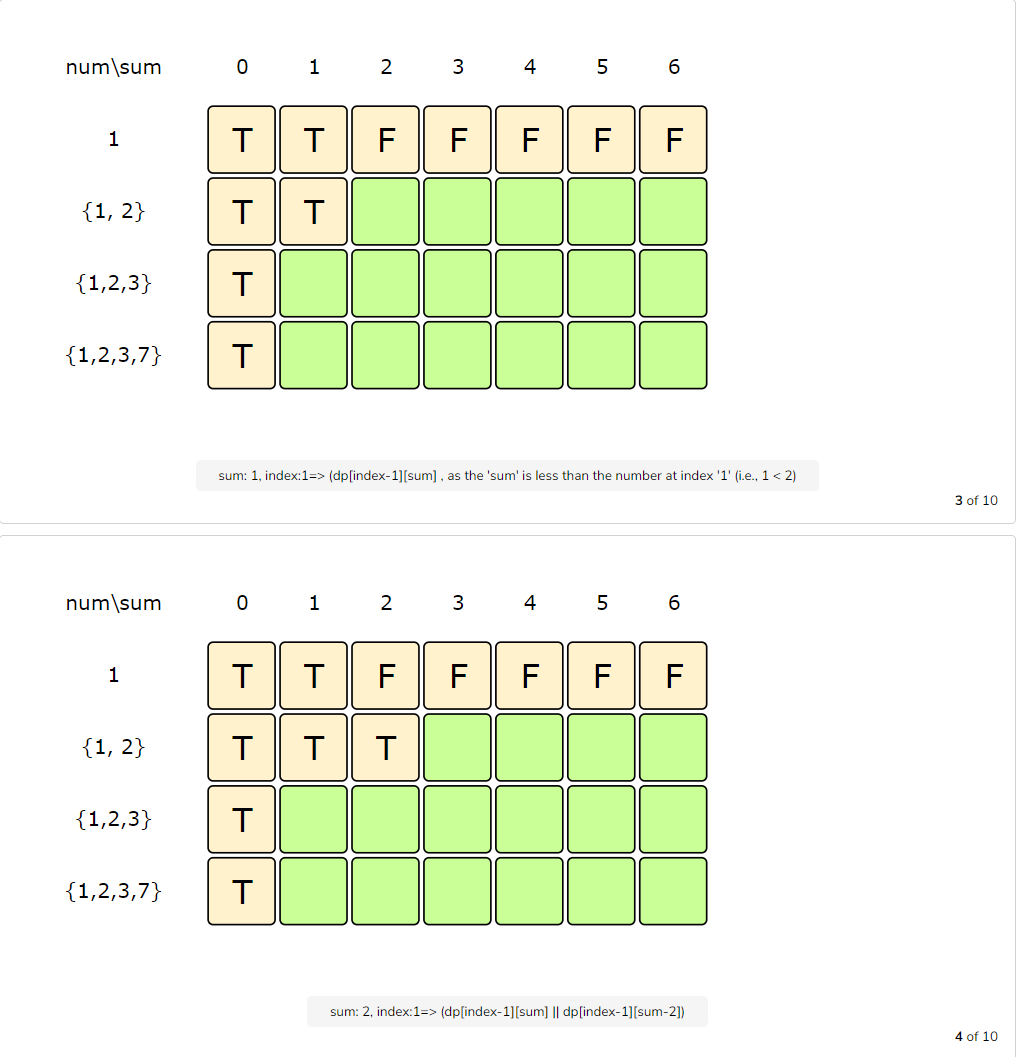
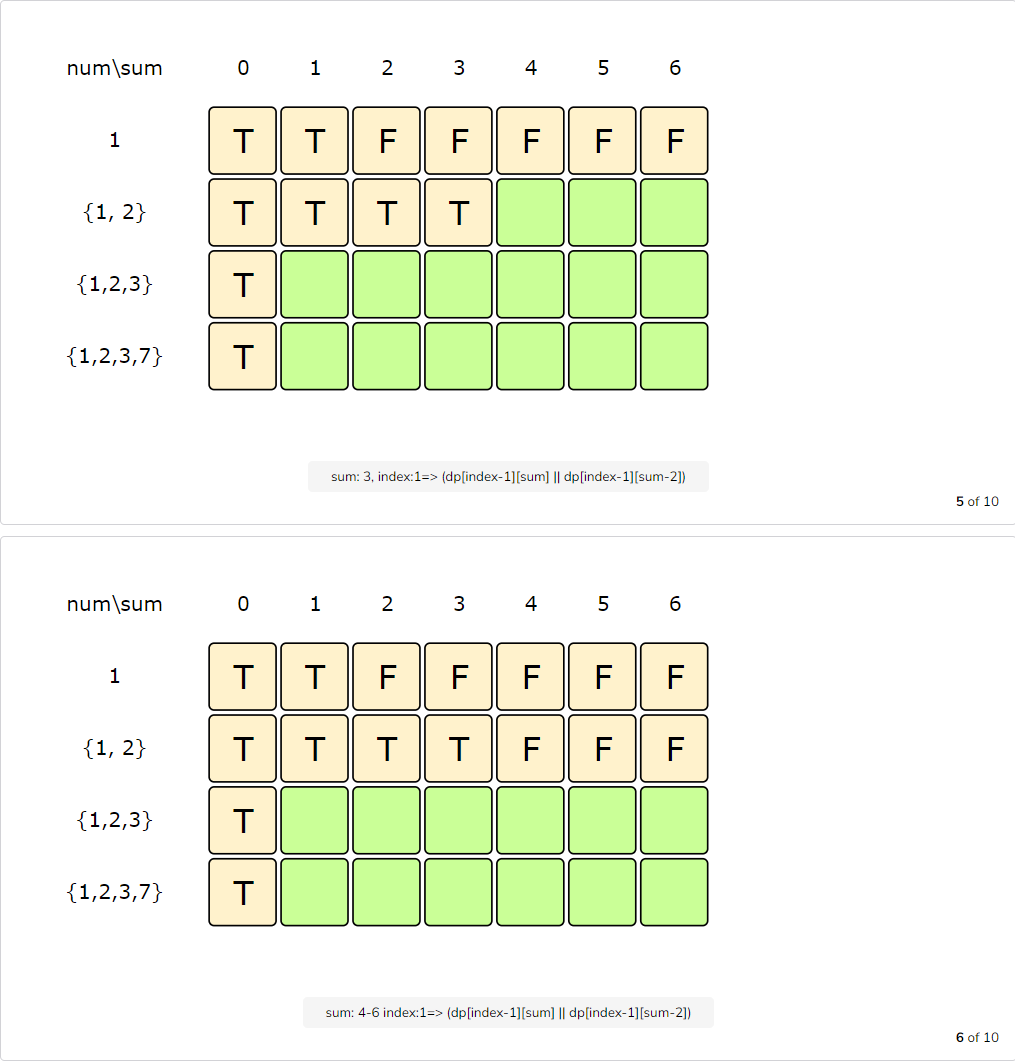
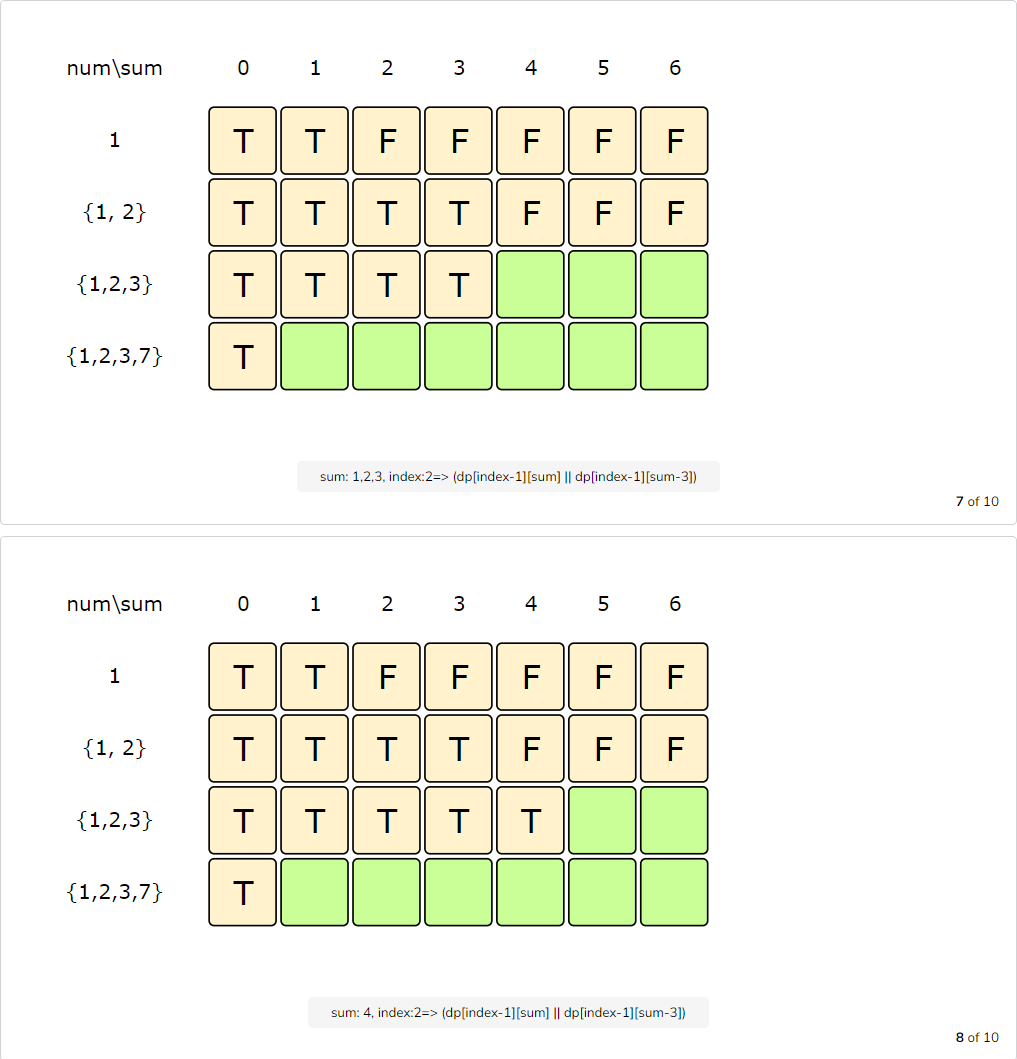
Code

Here is the code for our bottom-up dynamic programming approach:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
class Solution:
  def canPartition(self, num, sum):
    n = len(num)
    dp = [[False for x in range(sum+1)] for y in range(n)]

    # populate the sum = 0 columns, as we can always form '0' sum with an empty set
    for i in range(0, n):
      dp[i][0] = True

    # with only one number, we can form a subset only when the required sum is
    # equal to its value
    for s in range(1, sum+1):
      dp[0][s] = True if num[0] == s else False

    # process all subsets for all sums
    for i in range(1, n):
      for s in range(1, sum+1):
        # if we can get the sum 's' without the number at index 'i'
        if dp[i - 1][s]:
          dp[i][s] = dp[i - 1][s]
        elif s >= num[i]:
          # else include the number to see if we can find a subset to get the remaining sum
          dp[i][s] = dp[i - 1][s - num[i]]

    # the bottom-right corner will have our answer.
    return dp[n - 1][sum]


def main():
  sol = Solution()
  print("Can partition: " + str(sol.canPartition([1, 2, 3, 7], 6)))
  print("Can partition: " + str(sol.canPartition([1, 2, 7, 1, 5], 10)))
  print("Can partition: " + str(sol.canPartition([1, 3, 4, 8], 6)))


main()

Time and Space complexity

The above solution has the time and space complexity of O(N\S)*, where ‘N’ represents total numbers and ‘S’ is the required sum.

Challenge

Can we improve our bottom-up DP solution even further? Can you find an algorithm that has O(S) space complexity?

Hint

Similar to the space optimized solution for 0/1 Knapsack

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Solution:
  def canPartition(self, num, sum):
      n = len(num)
      dp = [False for x in range(sum+1)]

      # handle sum=0, as we can always have '0' sum with an empty set
      dp[0] = True

      # with only one number, we can have a subset only when the required sum is equal to 
      # its value
      for s in range(1, sum+1):
          dp[s] = num[0] == s

      # process all subsets for all sums
      for i in range(1, n):
          for s in range(sum, -1, -1):
              # if dp[s]==true, this means we can get the sum 's' without num[i], hence we 
              # can move on to the next number else we can include num[i] and see if we 
              # can find a subset to get the remaining sum
              if not dp[s] and s >= num[i]:
                  dp[s] = dp[s - num[i]]

      return dp[sum]


def main():
  sol = Solution()
  print("Can partition: " + str(sol.canPartition([1, 2, 3, 7], 6)))
  print("Can partition: " + str(sol.canPartition([1, 2, 7, 1, 5], 10)))
  print("Can partition: " + str(sol.canPartition([1, 3, 4, 8], 6)))


main()

Minimum Subset Sum Difference (hard)

leetcode 2035 但是没有限制positive num，不太会了

Similar | 2035. Partition Array Into Two Arrays to Minimize Sum Difference Design Gurus Educative.io

Problem Statement

Given a set of positive numbers, partition the set into two subsets with minimum difference between their subset sums.

Example 1:

1
2
3
4
Input: {1, 2, 3, 9}
Output: 3
Explanation: We can partition the given set into two subsets where minimum absolute difference 
between the sum of numbers is '3'. Following are the two subsets: {1, 2, 3} & {9}.

Example 2:

1
2
3
4
Input: {1, 2, 7, 1, 5}
Output: 0
Explanation: We can partition the given set into two subsets where minimum absolute difference 
between the sum of number is '0'. Following are the two subsets: {1, 2, 5} & {7, 1}.

Example 3:

1
2
3
4
Input: {1, 3, 100, 4}
Output: 92
Explanation: We can partition the given set into two subsets where minimum absolute difference 
between the sum of numbers is '92'. Here are the two subsets: {1, 3, 4} & {100}.

Constraints:

  • 1 <= num.length <= 200
  • 1 <= num[i] <= 100

Basic Solution

This problem follows the 0/1 Knapsack pattern and can be converted into a Subset Sum problem.

Let’s assume S1 and S2 are the two desired subsets. A basic brute-force solution could be to try adding each element either in S1 or S2 in order to find the combination that gives the minimum sum difference between the two sets.

So our brute-force algorithm will look like:

Code

Here is the code for the brute-force solution:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution:
  def canPartition(self, num):
    return self.can_partition_recursive(num, 0, 0, 0)


  def can_partition_recursive(self, num, currentIndex, sum1, sum2):
    # base check
    if currentIndex == len(num):
      return abs(sum1 - sum2)

    # recursive call after including the number at the currentIndex in the first set
    diff1 = self.can_partition_recursive(
      num, currentIndex + 1, sum1 + num[currentIndex], sum2)

    # recursive call after including the number at the currentIndex in the second set
    diff2 = self.can_partition_recursive(
      num, currentIndex + 1, sum1, sum2 + num[currentIndex])

    return min(diff1, diff2)


def main():
  sol = Solution()
  print("Can partition: " + str(sol.canPartition([1, 2, 3, 9])))
  print("Can partition: " + str(sol.canPartition([1, 2, 7, 1, 5])))
  print("Can partition: " + str(sol.canPartition([1, 3, 100, 4])))


main()

Time and Space complexity

Because of the two recursive calls, the time complexity of the above algorithm is exponential O(2^n), where ‘n’ represents the total number. The space complexity is O(n) which is used to store the recursion stack.

Top-down Dynamic Programming with Memoization

We can use memoization to overcome the overlapping sub-problems.

We will be using a two-dimensional array to store the results of the solved sub-problems. We can uniquely identify a sub-problem from ‘currentIndex’ and ‘Sum1’ as ‘Sum2’ will always be the sum of the remaining numbers.

Code

Here is the code:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
class Solution:
  def canPartition(self, num):
    s = sum(num)
    dp = [[-1 for x in range(s+1)] for y in range(len(num))]
    return self.can_partition_recursive(dp, num, 0, 0, 0)


  def can_partition_recursive(self, dp, num, currentIndex, sum1, sum2):
    # base check
    if currentIndex == len(num):
      return abs(sum1 - sum2)

    # check if we have not already processed similar problem
    if dp[currentIndex][sum1] == -1:
      # recursive call after including the number at the currentIndex in the first set
      diff1 = self.can_partition_recursive(
        dp, num, currentIndex + 1, sum1 + num[currentIndex], sum2)

      # recursive call after including the number at the currentIndex in the second set
      diff2 = self.can_partition_recursive(
        dp, num, currentIndex + 1, sum1, sum2 + num[currentIndex])

      dp[currentIndex][sum1] = min(diff1, diff2)

    return dp[currentIndex][sum1]


def main():
  sol = Solution()
  print("Can partition: " + str(sol.canPartition([1, 2, 3, 9])))
  print("Can partition: " + str(sol.canPartition([1, 2, 7, 1, 5])))
  print("Can partition: " + str(sol.canPartition([1, 3, 100, 4])))


main()

Bottom-up Dynamic Programming

Let’s assume ‘S’ represents the total sum of all the numbers. So, in this problem, we are trying to find a subset whose sum is as close to ‘S/2’ as possible, because if we can partition the given set into two subsets of an equal sum, we get the minimum difference, i.e. zero. This transforms our problem to Subset Sum, where we try to find a subset whose sum is equal to a given number— ‘S/2’ in our case. If we can’t find such a subset, then we will take the subset which has the sum closest to ‘S/2’. This is easily possible, as we will be calculating all possible sums with every subset.

Essentially, we need to calculate all the possible sums up to ‘S/2’ for all numbers. So how can we populate the array db[TotalNumbers][S/2+1] in the bottom-up fashion?

For every possible sum ‘s’ (where 0 <= s <= S/2), we have two options:

  1. Exclude the number. In this case, we will see if we can get the sum ‘s’ from the subset excluding this number => dp[index-1][s]
  2. Include the number if its value is not more than ‘s’. In this case, we will see if we can find a subset to get the remaining sum => dp[index-1][s-num[index]]

If either of the two above scenarios is true, we can find a subset with a sum equal to ‘s’. We should dig into this before we can learn how to find the closest subset.

Let’s draw this visually, with the example input {1, 2, 3, 9}. Since the total sum is ‘15’, we will try to find a subset whose sum is equal to the half of it, i.e. ‘7’.

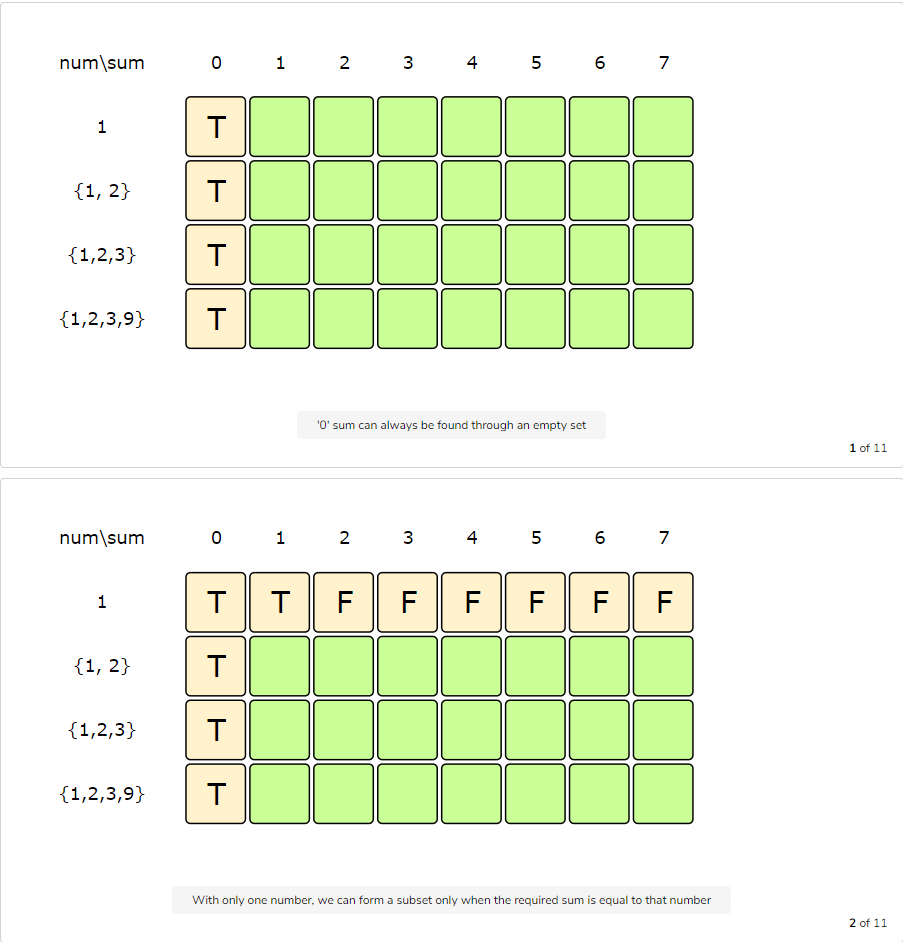
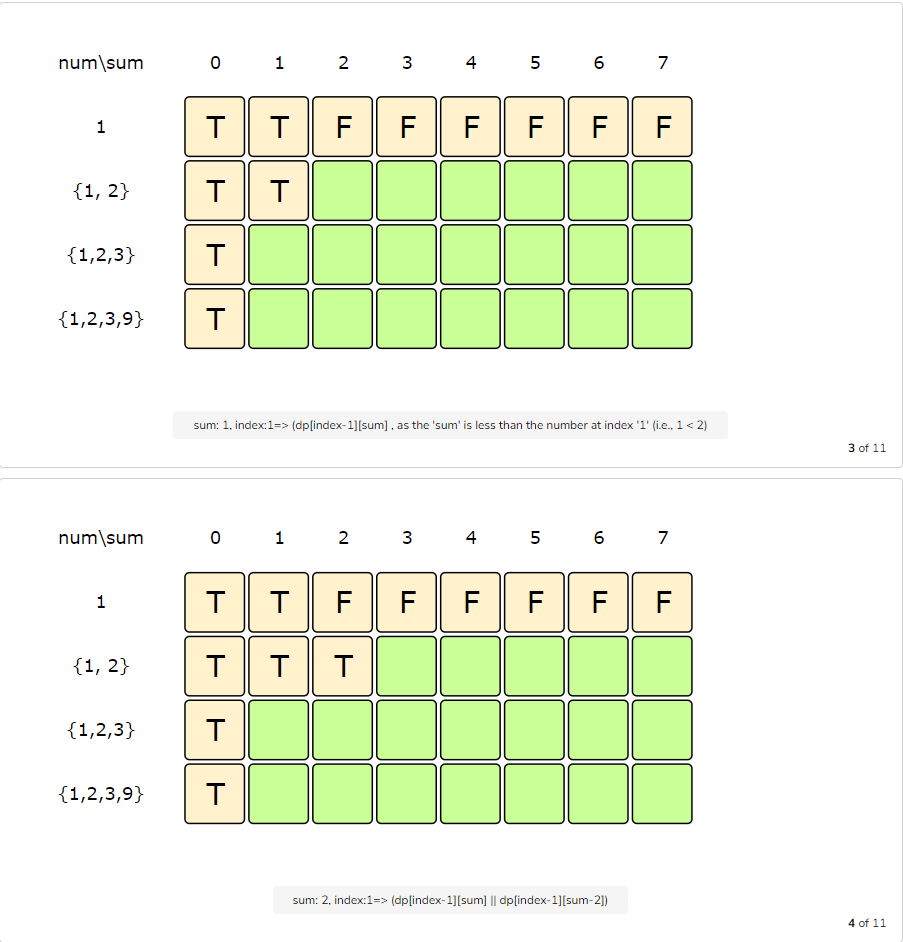
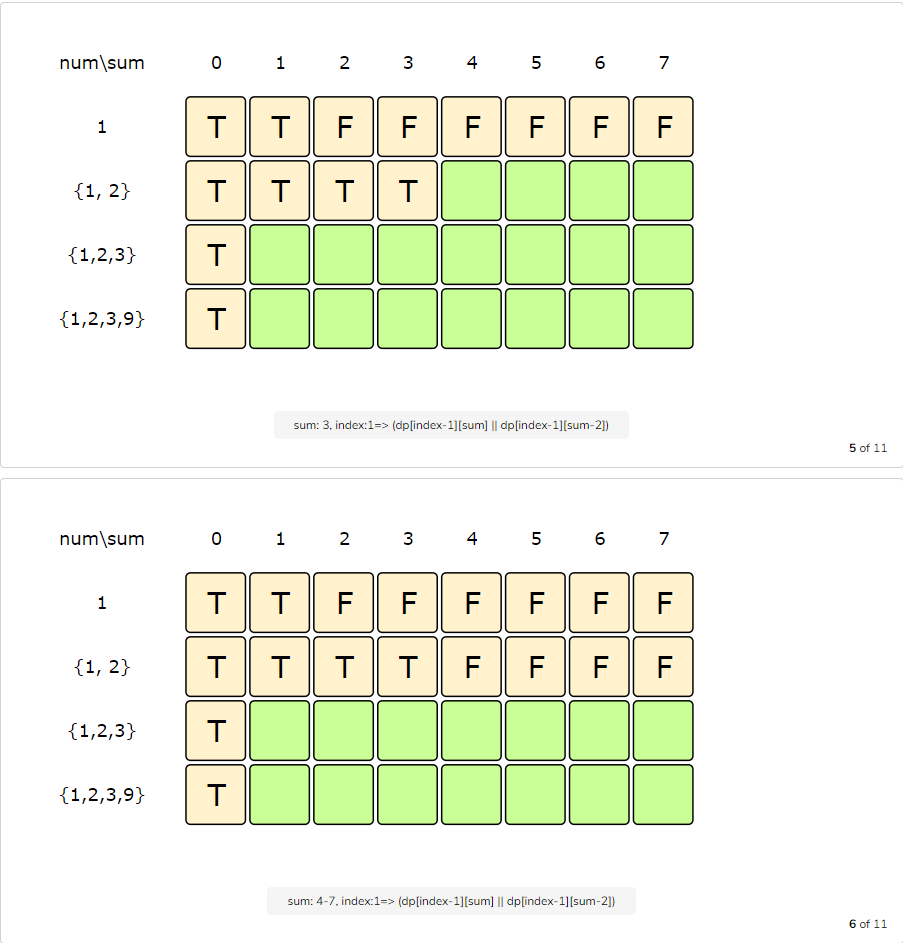
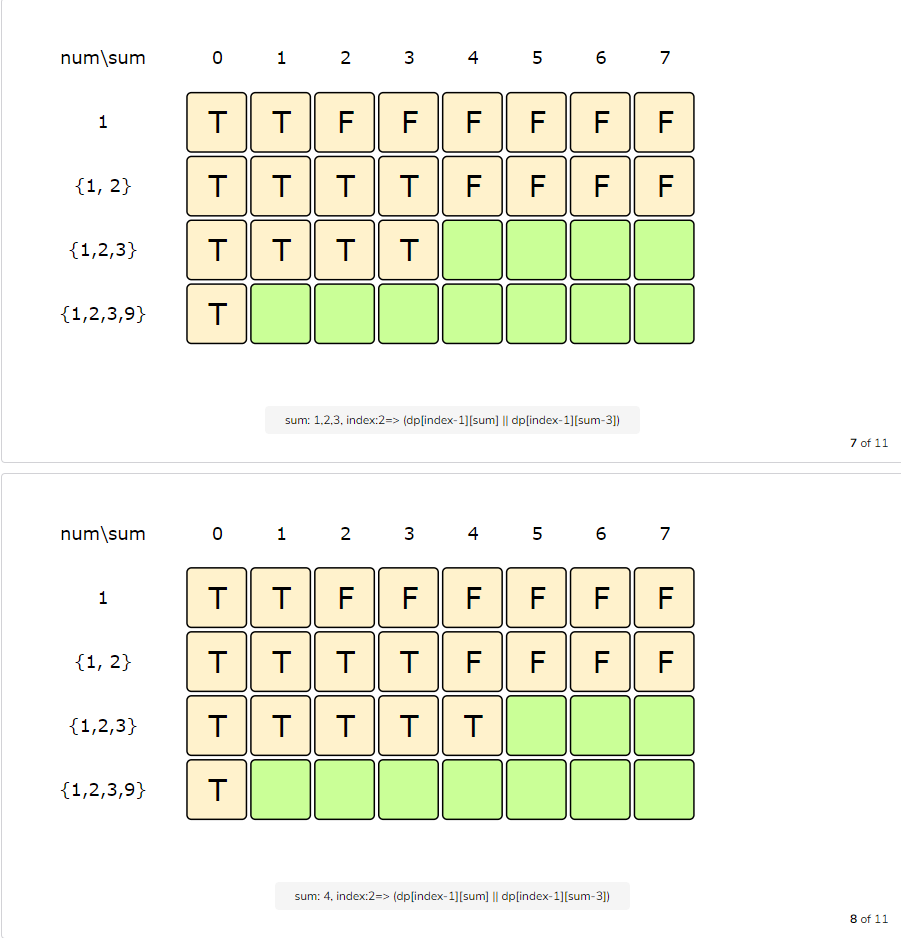
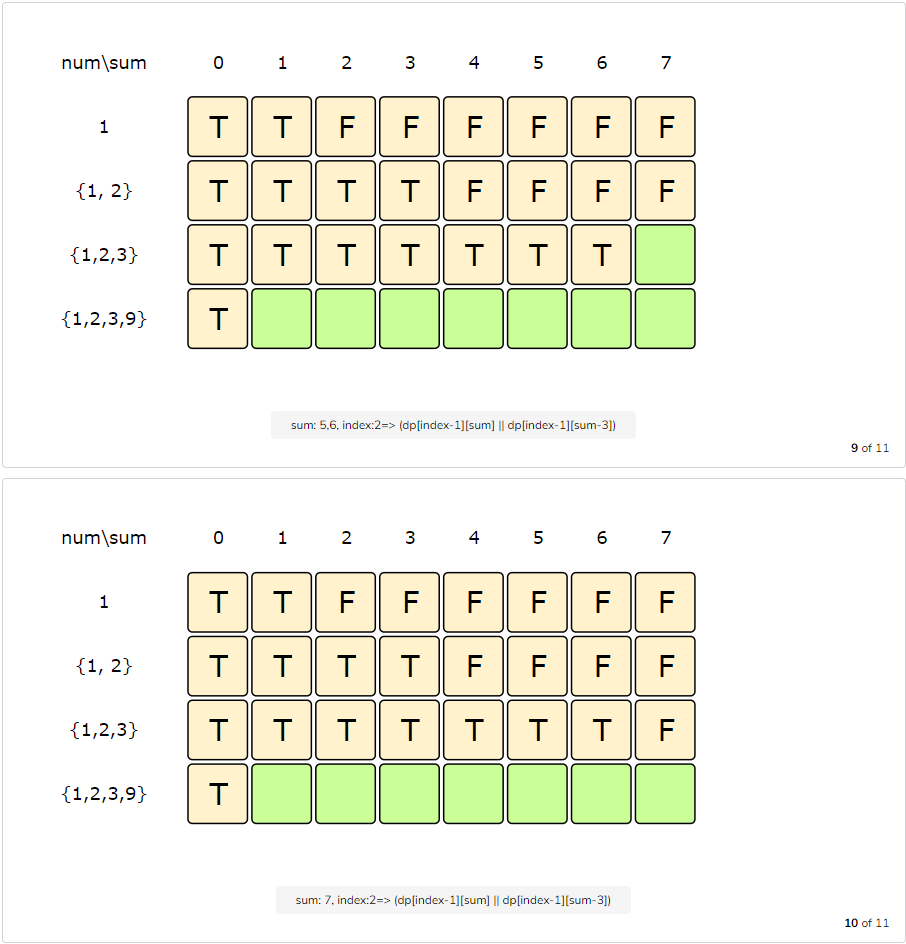
The above visualization tells us that it is not possible to find a subset whose sum is equal to ‘7’. So what is the closest subset we can find? We can find the subset if we start moving backwards in the last row from the bottom right corner to find the first ‘T’. The first “T” in the diagram above is the sum ‘6’, which means that we can find a subset whose sum is equal to ‘6’. This means the other set will have a sum of ‘9’ and the minimum difference will be ‘3’.

Code

Here is the code for our bottom-up dynamic programming approach:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
class Solution:
  def canPartition(self, num):
    s = sum(num)
    n = len(num)
    dp = [[False for x in range(int(s/2)+1)] for y in range(n)]

    # populate the s=0 columns, as we can always form '0' sum with an empty set
    for i in range(0, n):
      dp[i][0] = True

    # with only one number, we can form a subset only when the required sum is equal to 
    # that number
    for j in range(0, int(s/2)+1):
      dp[0][j] = num[0] == j

    # process all subsets for all sums
    for i in range(1, n):
      for j in range(1, int(s/2)+1):
        # if we can get the sum 's' without the number at index 'i'
        if dp[i - 1][j]:
          dp[i][j] = dp[i - 1][j]
        elif j >= num[i]:
          # else include the number and see if we can find a subset to get remaining sum
          dp[i][j] = dp[i - 1][j - num[i]]

    sum1 = 0
    # find the largest index in the last row which is true
    for i in range(int(s/2), -1, -1):
      if dp[n - 1][i]:
        sum1 = i
        break

    sum2 = s - sum1
    return abs(sum2 - sum1)


def main():
  sol = Solution()
  print("Can partition: " + str(sol.canPartition([1, 2, 3, 9])))
  print("Can partition: " + str(sol.canPartition([1, 2, 7, 1, 5])))
  print("Can partition: " + str(sol.canPartition([1, 3, 100, 4])))


main()

Time and Space complexity

The above solution has the time and space complexity of O(N\S)*, where ‘N’ represents total numbers and ‘S’ is the total sum of all the numbers.

Problem Challenge 1

Similar | Top Interview 150 | 39. Combination Sum Design Gurus Educative.io

Count of Subset Sum (hard)

Given a set of positive numbers, find the total number of subsets whose sum is equal to a given number ‘S’.

Example 1: 

1
2
3
4
Input: {1, 1, 2, 3}, S=4
Output: 3
The given set has '3' subsets whose sum is '4': {1, 1, 2}, {1, 3}, {1, 3}
Note that we have two similar sets {1, 3}, because we have two '1' in our input.

Example 2:

1
2
3
Input: {1, 2, 7, 1, 5}, S=9
Output: 3
The given set has '3' subsets whose sum is '9': {2, 7}, {1, 7, 1}, {1, 2, 1, 5}

Constraints:

  • 1 <= num.length <= 20
  • 0 <= num[i] <= 1000
  • 0 <= sum(num[i]) <= 1000
  • -1000 <= S <= 1000

Basic Solution

This problem follows the 0/1 Knapsack pattern and is quite similar to Subset Sum. The only difference in this problem is that we need to count the number of subsets, whereas in Subset Sum we only wanted to know if a subset with the given sum existed.

A basic brute-force solution could be to try all subsets of the given numbers to count the subsets that have a sum equal to ‘S’. So our brute-force algorithm will look like:

Code

Here is the code for the brute-force solution:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Solution:
  def countSubsets(self, num, sum):
    return self.count_subsets_recursive(num, sum, 0)


  def count_subsets_recursive(self, num, sum, currentIndex):
    # base checks
    if sum == 0:
      return 1
    n = len(num)
    if n == 0 or currentIndex >= n:
      return 0

    # recursive call after selecting the number at the currentIndex
    # if the number at currentIndex exceeds the sum, we shouldn't process this
    sum1 = 0
    if num[currentIndex] <= sum:
      sum1 = self.count_subsets_recursive(
        num, sum - num[currentIndex], currentIndex + 1)

    # recursive call after excluding the number at the currentIndex
    sum2 = self.count_subsets_recursive(num, sum, currentIndex + 1)

    return sum1 + sum2


def main():
  sol = Solution()
  print("Total number of subsets " + str(sol.countSubsets([1, 1, 2, 3], 4)))
  print("Total number of subsets: " + str(sol.countSubsets([1, 2, 7, 1, 5], 9)))


main()

Time and Space complexity

The time complexity of the above algorithm is exponential O(2^n), where ‘n’ represents the total number. The space complexity is O(n), this memory is used to store the recursion stack.

Top-down Dynamic Programming with Memoization

We can use memoization to overcome the overlapping sub-problems. We will be using a two-dimensional array to store the results of solved sub-problems. As mentioned above, we need to store results for every subset and for every possible sum.

Code

Here is the code:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
class Solution:
  def countSubsets(self, num, sum):
    # create a two dimensional array for Memoization, each element is initialized to '-1'
    dp = [[-1 for x in range(sum+1)] for y in range(len(num))]
    return self.count_subsets_recursive(dp, num, sum, 0)


  def count_subsets_recursive(self, dp, num, sum, currentIndex):
    # base checks
    if sum == 0:
      return 1

    n = len(num)
    if n == 0 or currentIndex >= n:
      return 0

    # check if we have not already processed a similar problem
    if dp[currentIndex][sum] == -1:
      # recursive call after choosing the number at the currentIndex
      # if the number at currentIndex exceeds the sum, we shouldn't process this
      sum1 = 0
      if num[currentIndex] <= sum:
        sum1 = self.count_subsets_recursive(
          dp, num, sum - num[currentIndex], currentIndex + 1)

      # recursive call after excluding the number at the currentIndex
      sum2 = self.count_subsets_recursive(dp, num, sum, currentIndex + 1)

      dp[currentIndex][sum] = sum1 + sum2

    return dp[currentIndex][sum]


def main():
  sol = Solution()
  print("Total number of subsets " + str(sol.countSubsets([1, 1, 2, 3], 4)))
  print("Total number of subsets: " + str(sol.countSubsets([1, 2, 7, 1, 5], 9)))


main()

Bottom-up Dynamic Programming

We will try to find if we can make all possible sums with every subset to populate the array db[TotalNumbers][S+1].

So, at every step we have two options:

  1. Exclude the number. Count all the subsets without the given number up to the given sum => dp[index-1][sum]
  2. Include the number if its value is not more than the ‘sum’. In this case, we will count all the subsets to get the remaining sum => dp[index-1][sum-num[index]]

To find the total sets, we will add both of the above two values:

1
dp[index][sum] = dp[index-1][sum] + dp[index-1][sum-num[index]])

Let’s start with our base case of size zero:

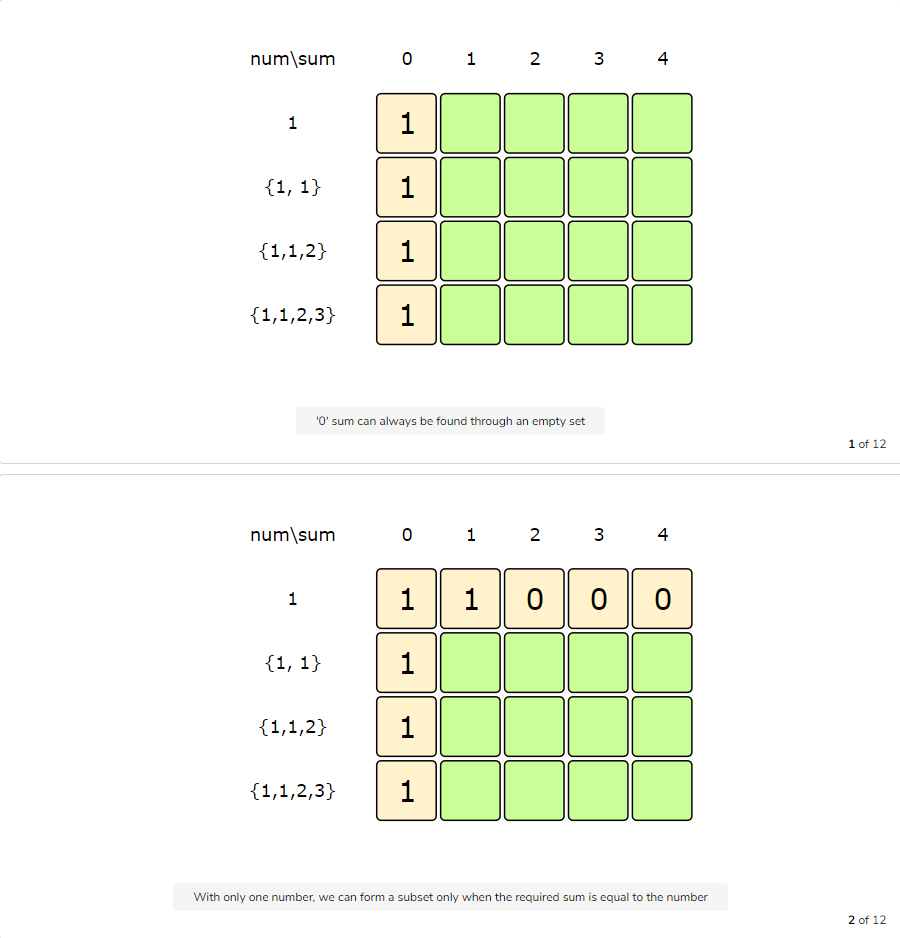
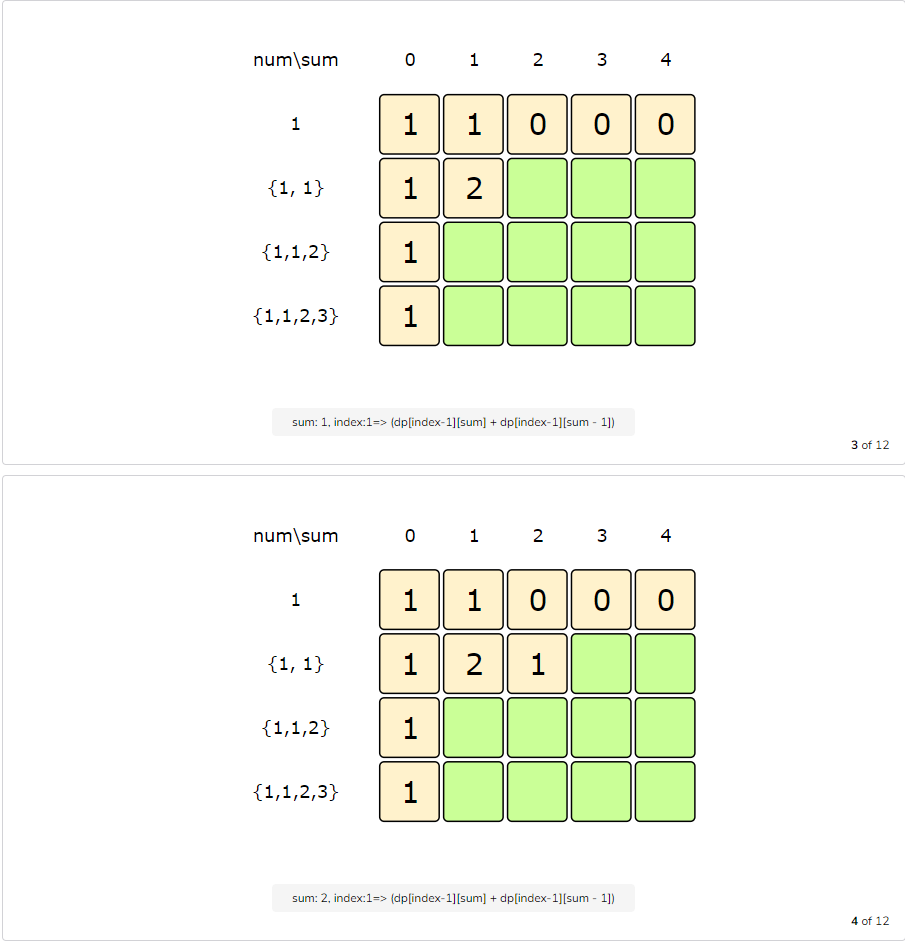
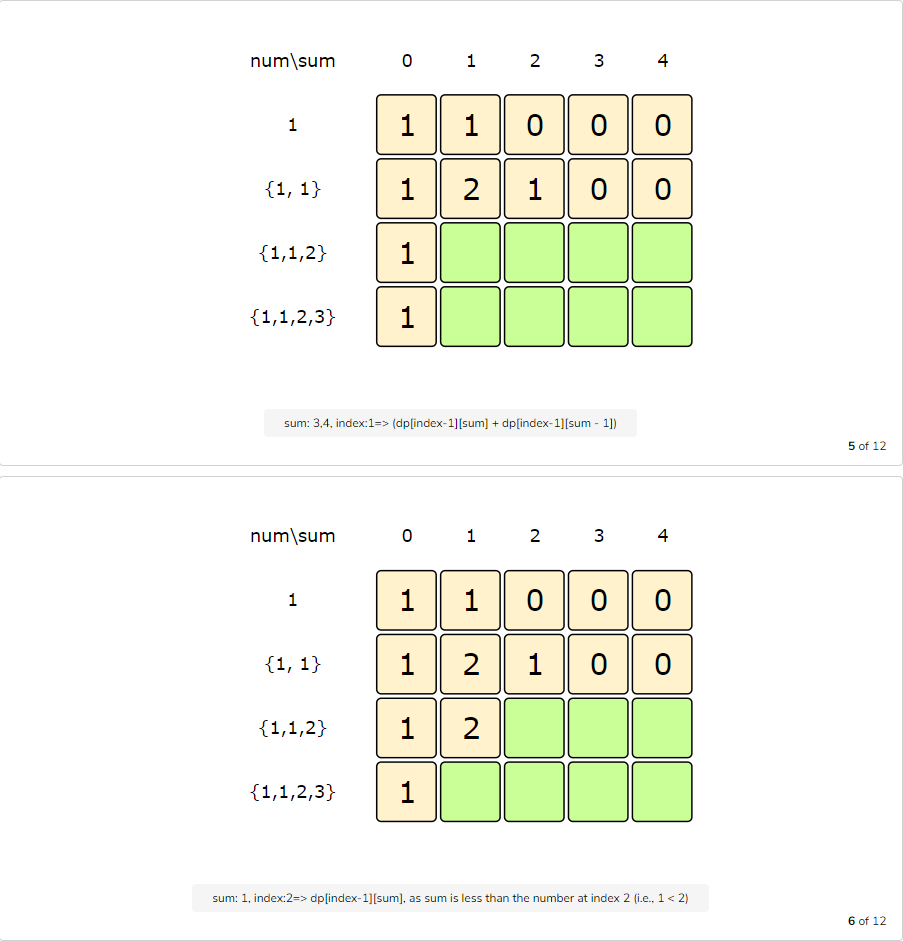
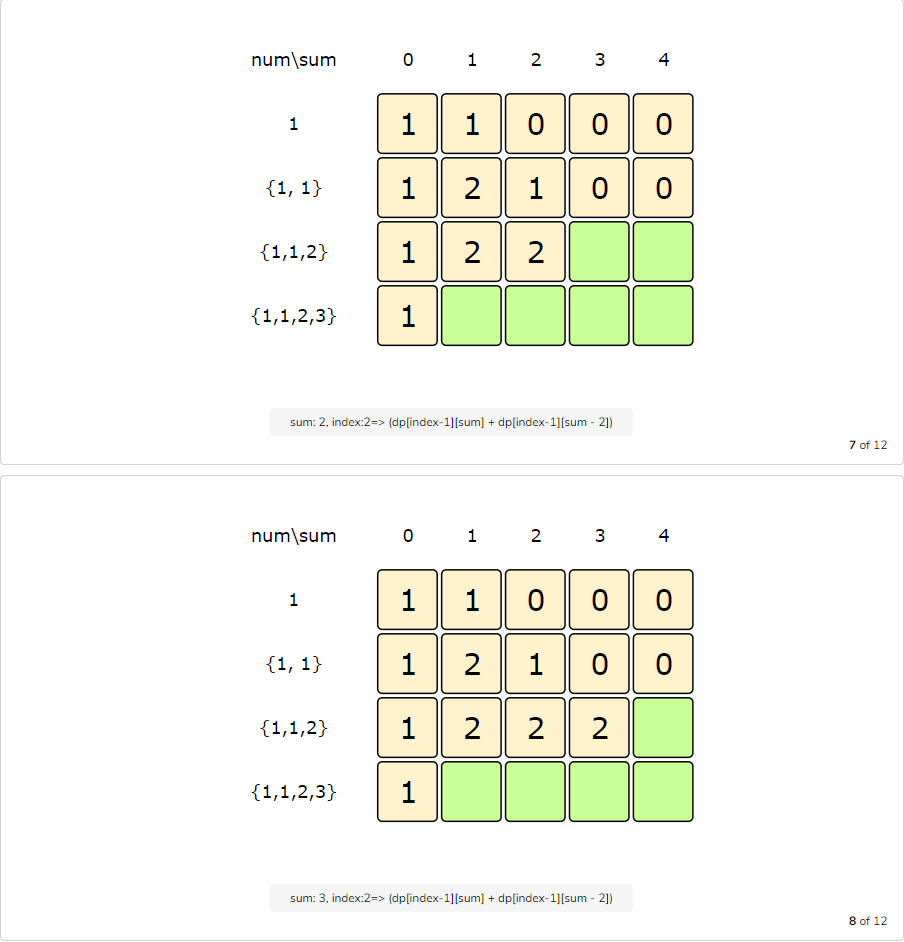
Code

Here is the code for our bottom-up dynamic programming approach:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class Solution:
  def countSubsets(self, num, sum):
    n = len(num)
    dp = [[-1 for x in range(sum+1)] for y in range(n)]

    # populate the sum = 0 columns, as we will always have an empty set for zero sum
    for i in range(0, n):
      dp[i][0] = 1

    # with only one number, we can form a subset only when the required sum is
    # equal to its value
    for s in range(1, sum+1):
      dp[0][s] = 1 if num[0] == s else 0

    # process all subsets for all sums
    for i in range(1, n):
      for s in range(1, sum+1):
        # exclude the number
        dp[i][s] = dp[i - 1][s]
        # include the number, if it does not exceed the sum
        if s >= num[i]:
          dp[i][s] += dp[i - 1][s - num[i]]

    # the bottom-right corner will have our answer.
    return dp[n - 1][sum]


def main():
  sol = Solution()
  print("Total number of subsets " + str(sol.countSubsets([1, 1, 2, 3], 4)))
  print("Total number of subsets: " + str(sol.countSubsets([1, 2, 7, 1, 5], 9)))


main()

Time and Space complexity

The above solution has the time and space complexity of O(N\S)*, where ‘N’ represents total numbers and ‘S’ is the desired sum.

Challenge

Can we improve our bottom-up DP solution even further? Can you find an algorithm that has O(S) space complexity?

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution:
  def countSubsets(self, num, sum):
    n = len(num)
    dp = [0 for x in range(sum+1)]
    dp[0] = 1

    # with only one number, we can form a subset only when the required sum is equal 
    # to the number
    for s in range(1, sum+1):
      dp[s] = 1 if num[0] == s else 0

    # process all subsets for all sums
    for i in range(1, n):
      for s in range(sum, -1, -1):
        if s >= num[i]:
          dp[s] += dp[s - num[i]]

    return dp[sum]


def main():
  sol = Solution()
  print("Total number of subsets " + str(sol.countSubsets([1, 1, 2, 3], 4)))
  print("Total number of subsets: " + str(sol.countSubsets([1, 2, 7, 1, 5], 9)))


main()

Problem Challenge 2

leetcode 494, leetcode里有0，不太会，尝试了两次都失败了

Similar | 494. Target Sum Design Gurus Educative.io

Target Sum (hard)

You are given a set of positive numbers and a target sum ‘S’. Each number should be assigned either a ‘+’ or ‘-’ sign. We need to find the total ways to assign symbols to make the sum of the numbers equal to the target ‘S’.

Example 1:

1
2
3
Input: {1, 1, 2, 3}, S=1
Output: 3
Explanation: The given set has '3' ways to make a sum of '1': {+1-1-2+3} & {-1+1-2+3} & {+1+1+2-3}

Example 2:

1
2
3
Input: {1, 2, 7, 1}, S=9
Output: 2
Explanation: The given set has '2' ways to make a sum of '9': {+1+2+7-1} & {-1+2+7+1}

Constraints:

  • 1 <= num.length <= 20
  • 0 <= num[i] <= 1000
  • 0 <= sum(num[i]) <= 1000
  • -1000 <= S <= 1000

Solution

This problem follows the 0/1 Knapsack pattern and can be converted into Count of Subset Sum. Let’s dig into this.

We are asked to find two subsets of the given numbers whose difference is equal to the given target ‘S’. Take the first example above. As we saw, one solution is {+1-1-2+3}. So, the two subsets we are asked to find are {1, 3} & {1, 2} because,

1
(1 + 3) - (1 + 2 ) = 1

Now, let’s say ‘Sum(s1)’ denotes the total sum of set ‘s1’, and ‘Sum(s2)’ denotes the total sum of set ‘s2’. So the required equation is:

1
Sum(s1) - Sum(s2) = S

This equation can be reduced to the subset sum problem. Let’s assume that ‘Sum(num)’ denotes the total sum of all the numbers, therefore:

1
Sum(s1) + Sum(s2) = Sum(num)

Let’s add the above two equations:

1
2
3
=> Sum(s1) - Sum(s2) + Sum(s1) + Sum(s2) = S + Sum(num)
=> 2 * Sum(s1) =  S + Sum(num)
=> Sum(s1) = (S + Sum(num)) / 2

Which means that one of the set ‘s1’ has a sum equal to (S + Sum(num)) / 2. This essentially converts our problem to: “Find the count of subsets of the given numbers whose sum is equal to (S + Sum(num)) / 2“

Code

Let’s take the dynamic programming code of Count of Subset Sum and extend it to solve this problem:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
class Solution:
  def findTargetSubsets(self, num, s):
    totalSum = sum(num)

    # if 's + totalSum' is odd, we cannot find a subset with the sum equal 
    # to '(s + totalSum) / 2'
    if totalSum < s or (s + totalSum) % 2 == 1:
      return 0

    return self.count_subsets(num, (s + totalSum) // 2)


  # this function is exactly similar to what we have in 'Count of Subset Sum' problem.
  def count_subsets(self, num, s):
    n = len(num)
    dp = [[0 for x in range(s+1)] for y in range(n)]

    # populate the sum = 0 columns, as we will always have an empty set for zero sum
    for i in range(0, n):
      dp[i][0] = 1

    # with only one number, we can form a subset only when the required sum is
    # equal to the number
    for s in range(1, s+1):
      dp[0][s] = 1 if num[0] == s else 0

    # process all subsets for all sums
    for i in range(1, n):
      for s in range(1, s+1):
        dp[i][s] = dp[i - 1][s]
        if s >= num[i]:
          dp[i][s] += dp[i - 1][s - num[i]]

    # the bottom-right corner will have our answer.
    return dp[n - 1][s]


def main():
  sol = Solution()
  print("Total ways: " + str(sol.findTargetSubsets([1, 1, 2, 3], 1)))
  print("Total ways: " + str(sol.findTargetSubsets([1, 2, 7, 1], 9)))


main()

Time and Space complexity

The above solution has time and space complexity of O(N*S), where ‘N’ represents total numbers and ‘S’ is the desired sum.

We can further improve the solution to use only O(S) space.

Space Optimized Solution

Here is the code for the space-optimized solution, using only a single array:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
class Solution:
  def findTargetSubsets(self, num, s):
    totalSum = sum(num)

    # if 's + totalSum' is odd, we can't find a subset with sum equal to '(s +totalSum)/2'
    if totalSum < s or (s + totalSum) % 2 == 1:
      return 0

    return self.count_subsets(num, (s + totalSum) // 2)


  # this function is exactly similar to what we have in 'Count of Subset Sum' problem
  def count_subsets(self, num, sum):
    n = len(num)
    dp = [0 for x in range(sum+1)]
    dp[0] = 1

    # with only one number, we can form a subset only when the required sum is equal to 
    # the number
    for s in range(1, sum+1):
      dp[s] = 1 if num[0] == s else 0

    # process all subsets for all sums
    for i in range(1, n):
      for s in range(sum, -1, -1):
        if s >= num[i]:
          dp[s] += dp[s - num[i]]

    return dp[sum]


def main():
  sol = Solution()
  print("Total ways: " + str(sol.findTargetSubsets([1, 1, 2, 3], 1)))
  print("Total ways: " + str(sol.findTargetSubsets([1, 2, 7, 1], 9)))


main()

Author：Hasuer

Link：https://hasuer.github.io/21-pattern-01-knapsack-dynamic-programming/index.html

Publish date：May 21st 2024, 10:10:23 am

Update date：May 28th 2024, 11:30:17 am

License：本文采用知识共享署名-非商业性使用 4.0 国际许可协议进行许可

CATALOG
  1. 1. Introduction
  2. 2. *0/1 Knapsack (medium)
    1. 2.1. Introduction
    2. 2.2. Problem Statement
    3. 2.3. Basic Solution
      1. 2.3.1. Code
      2. 2.3.2. Time and Space complexity
    4. 2.4. Top-down Dynamic Programming with Memoization
      1. 2.4.1. Code
      2. 2.4.2. Time and Space complexity
    5. 2.5. Bottom-up Dynamic Programming
      1. 2.5.1. Code
      2. 2.5.2. Time and Space complexity
      3. 2.5.3. How can we find the selected items?
    6. 2.6. Challenge
  3. 3. Equal Subset Sum Partition (medium)
    1. 3.1. Problem Statement
    2. 3.2. Basic Solution
      1. 3.2.1. Code
      2. 3.2.2. Time and Space complexity
    3. 3.3. Top-down Dynamic Programming with Memoization
      1. 3.3.1. Code
      2. 3.3.2. Time and Space complexity
    4. 3.4. Bottom-up Dynamic Programming
      1. 3.4.1. Code
      2. 3.4.2. Time and Space complexity
  4. 4. Subset Sum (medium)
    1. 4.1. Problem Statement
    2. 4.2. Basic Solution
    3. 4.3. Bottom-up Dynamic Programming
      1. 4.3.1. Code
      2. 4.3.2. Time and Space complexity
    4. 4.4. Challenge
  5. 5. Minimum Subset Sum Difference (hard)
    1. 5.1. Problem Statement
    2. 5.2. Basic Solution
      1. 5.2.1. Code
      2. 5.2.2. Time and Space complexity
    3. 5.3. Top-down Dynamic Programming with Memoization
      1. 5.3.1. Code
    4. 5.4. Bottom-up Dynamic Programming
      1. 5.4.1. Code
      2. 5.4.2. Time and Space complexity
  6. 6. Problem Challenge 1
    1. 6.1. Count of Subset Sum (hard)
    2. 6.2. Basic Solution
      1. 6.2.1. Code
      2. 6.2.2. Time and Space complexity
    3. 6.3. Top-down Dynamic Programming with Memoization
      1. 6.3.1. Code
    4. 6.4. Bottom-up Dynamic Programming
      1. 6.4.1. Code
      2. 6.4.2. Time and Space complexity
    5. 6.5. Challenge
  7. 7. Problem Challenge 2
    1. 7.1. Target Sum (hard)
    2. 7.2. Solution
      1. 7.2.1. Code
      2. 7.2.2. Time and Space complexity
    3. 7.3. Space Optimized Solution
Total : 41
2024
2022
2021
Interview
技术笔记 Grokking-Interview-Pattern