Hasuer's Studio.

2. Pattern Fast_Slow pointers

Grokking Interview Pattern Interview
Word count: 4.7kReading time: 29 min
2024/05/02

Introduction

The Fast & Slow pointer approach, also known as the Hare & Tortoise algorithm, is a pointer algorithm that uses two pointers which move through the array (or sequence/LinkedList) at different speeds. This approach is quite useful when dealing with cyclic LinkedLists or arrays.

By moving at different speeds (say, in a cyclic LinkedList), the algorithm proves that the two pointers are bound to meet. The fast pointer should catch the slow pointer once both the pointers are in a cyclic loop.

One of the famous problems solved using this technique was Finding a cycle in a LinkedList. Let’s jump onto this problem to understand the Fast & Slow pattern.

LinkedList Cycle (easy)

Top Interview 150 | 141. Linked List Cycle Design Gurus Educative.io

Problem Statement

Given the head of a Singly LinkedList, write a function to determine if the LinkedList has a cycle in it or not.

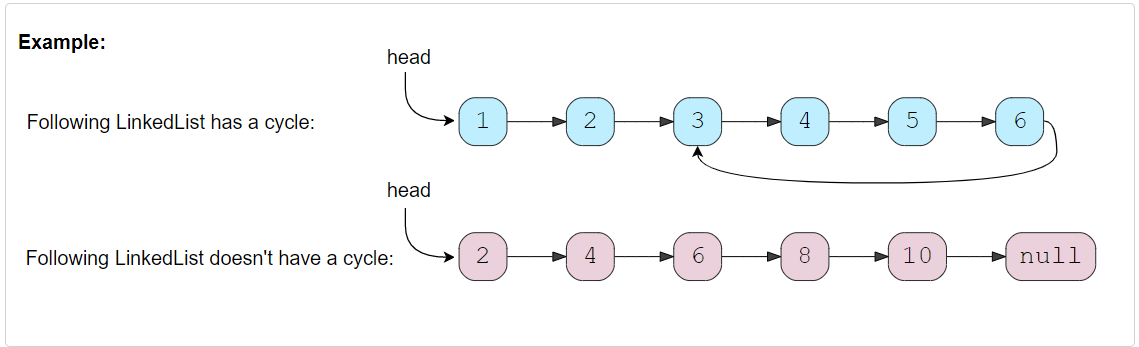
Constraints:

  • The number of the nodes in the list is in the range [0, 10^4].
  • 1 <= Node.val <= 10^5

Solution

Imagine two racers running in a circular racing track. If one racer is faster than the other, the faster racer is bound to catch up and cross the slower racer from behind. We can use this fact to devise an algorithm to determine if a LinkedList has a cycle in it or not.

Imagine we have a slow and a fast pointer to traverse the LinkedList. In each iteration, the slow pointer moves one step and the fast pointer moves two steps. This gives us two conclusions:

  1. If the LinkedList doesn’t have a cycle in it, the fast pointer will reach the end of the LinkedList before the slow pointer to reveal that there is no cycle in the LinkedList.
  2. The slow pointer will never be able to catch up to the fast pointer if there is no cycle in the LinkedList.

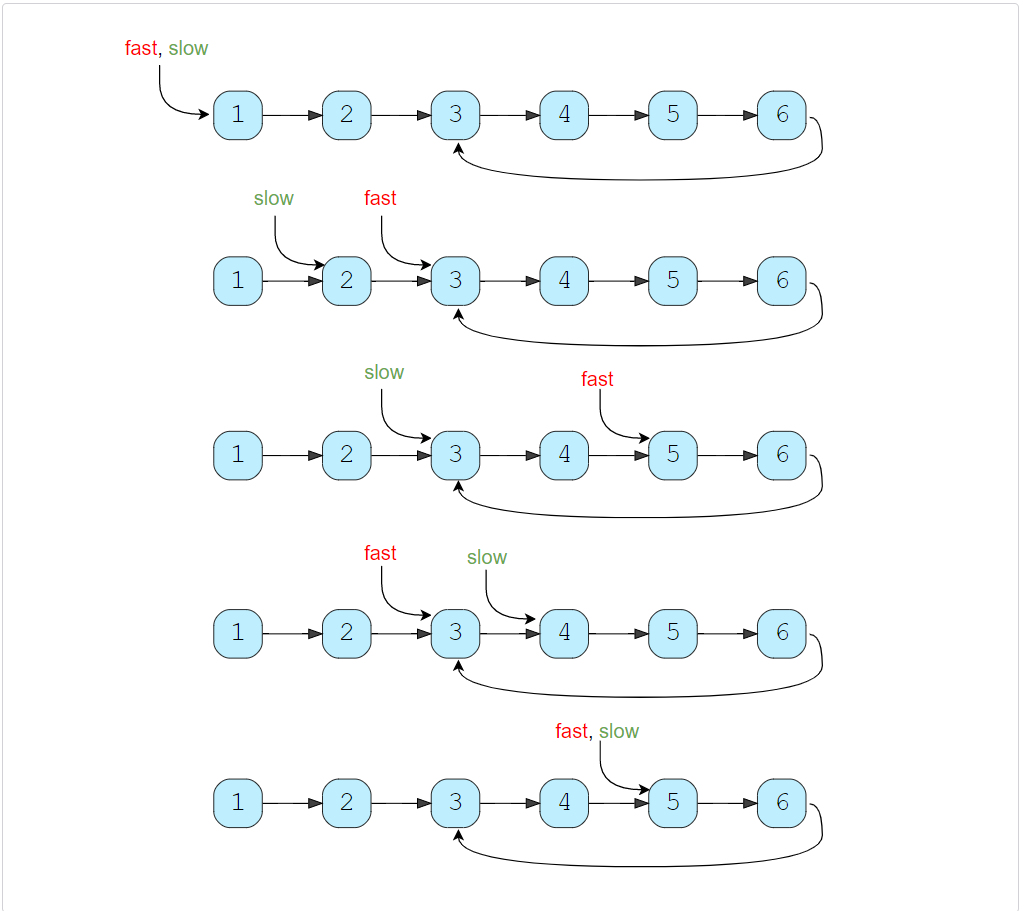
If the LinkedList has a cycle, the fast pointer enters the cycle first, followed by the slow pointer. After this, both pointers will keep moving in the cycle infinitely. If at any stage both of these pointers meet, we can conclude that the LinkedList has a cycle in it. Let’s analyze if it is possible for the two pointers to meet. When the fast pointer is approaching the slow pointer from behind we have two possibilities:

  1. The fast pointer is one step behind the slow pointer.
  2. The fast pointer is two steps behind the slow pointer.

All other distances between the fast and slow pointers will reduce to one of these two possibilities. Let’s analyze these scenarios, considering the fast pointer always moves first:

  1. If the fast pointer is one step behind the slow pointer: The fast pointer moves two steps and the slow pointer moves one step, and they both meet.
  2. If the fast pointer is two steps behind the slow pointer: The fast pointer moves two steps and the slow pointer moves one step. After the moves, the fast pointer will be one step behind the slow pointer, which reduces this scenario to the first scenario. This means that the two pointers will meet in the next iteration.

This concludes that the two pointers will definitely meet if the LinkedList has a cycle. A similar analysis can be done where the slow pointer moves first. Here is a visual representation of the above discussion:

Code

Here is what our algorithm will look like

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
#class Node:
#  def __init__(self, value, next=None):
#    self.val = value
#    self.next = next


class Solution:
  def hasCycle(self, head):
    slow, fast = head, head
    while fast is not None and fast.next is not None:
      fast = fast.next.next  # Move fast pointer two steps at a time
      slow = slow.next      # Move slow pointer one step at a time
      if slow == fast:      # Check if slow and fast pointers meet (cycle detected)
        return True         # Found a cycle in the linked list
    return False            # No cycle found in the linked list

def main():
  sol = Solution()
  head = Node(1)
  head.next = Node(2)
  head.next.next = Node(3)
  head.next.next.next = Node(4)
  head.next.next.next.next = Node(5)
  head.next.next.next.next.next = Node(6)
  print("LinkedList has cycle: " + str(sol.hasCycle(head)))

  head.next.next.next.next.next.next = head.next.next
  print("LinkedList has cycle: " + str(sol.hasCycle(head)))

  head.next.next.next.next.next.next = head.next.next.next
  print("LinkedList has cycle: " + str(sol.hasCycle(head)))

main()

Time Complexity

As we have concluded above, once the slow pointer enters the cycle, the fast pointer will meet the slow pointer in the same loop. Therefore, the time complexity of our algorithm will be O(N) where ‘N’ is the total number of nodes in the LinkedList.

Space Complexity

The algorithm runs in constant space O(1).

Similar Problems

Problem 1: Given the head of a LinkedList with a cycle, find the length of the cycle.

Solution: We can use the above solution to find the cycle in the LinkedList. Once the fast and slow pointers meet, we can save the slow pointer and iterate the whole cycle with another pointer until we see the slow pointer again to find the length of the cycle.

Here is what our algorithm will look like:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
#class Node:
#  def __init__(self, value, next=None):
#    self.val = value
#    self.next = next

class Solution:
  def findCycleLength(self, head):
    # Initialize slow and fast pointers to the head of the linked list
    slow, fast = head, head
    
    # Traverse the linked list using slow and fast pointers
    while fast is not None and fast.next is not None:
      # Move fast pointer two steps at a time and slow pointer one step at a time
      fast = fast.next.next
      slow = slow.next
      
      # Check if the slow and fast pointers meet, indicating the presence of a cycle
      if slow == fast:  # found the cycle
        return self.calculate_cycle_length(slow)

    return 0

  def calculate_cycle_length(self, slow):
    current = slow
    cycle_length = 0
    
    # Count the length of the cycle by moving through it
    while True:
      current = current.next
      cycle_length += 1
      
      # If we reach the starting point, we have completed a full cycle
      if current == slow:
        break
        
    return cycle_length

def main():
  sol = Solution()
  head = Node(1)
  head.next = Node(2)
  head.next.next = Node(3)
  head.next.next.next = Node(4)
  head.next.next.next.next = Node(5)
  head.next.next.next.next.next = Node(6)
  
  # Create a cycle in the linked list
  head.next.next.next.next.next.next = head.next.next
  
  # Find and print the length of the cycle
  print("LinkedList cycle length: " + str(sol.findCycleLength(head)))

  # Create a longer cycle in the linked list
  head.next.next.next.next.next.next = head.next.next.next
  
  # Find and print the length of the longer cycle
  print("LinkedList cycle length: " + str(sol.findCycleLength(head)))

main()

Time and Space Complexity: The above algorithm runs in O(N) time complexity and O(1) space complexity.

Start of LinkedList Cycle (medium)

142. Linked List Cycle II Design Gurus Educative.io

Problem Statement

Given the head of a Singly LinkedList that contains a cycle, write a function to find the starting node of the cycle.

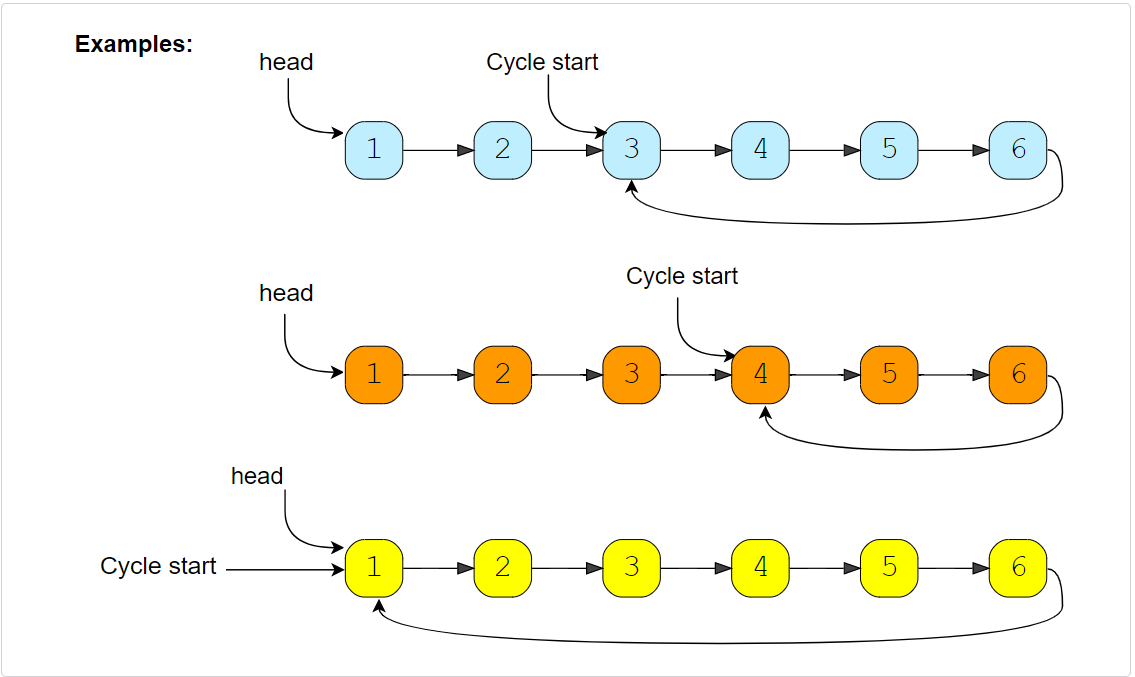
Solution

If we know the length of the LinkedList cycle, we can find the start of the cycle through the following steps:

  1. Take two pointers. Let’s call them pointer1 and pointer2.
  2. Initialize both pointers to point to the start of the LinkedList.
  3. We can find the length of the LinkedList cycle using the approach discussed in LinkedList Cycle. Let’s assume that the length of the cycle is ‘K’ nodes.
  4. Move pointer2 ahead by ‘K’ nodes.
  5. Now, keep incrementing pointer1 and pointer2 until they both meet.
  6. As pointer2 is ‘K’ nodes ahead of pointer1, which means, pointer2 must have completed one loop in the cycle when both pointers meet. Their meeting point will be the start of the cycle.

Let’s visually see this with the above-mentioned Example-1:

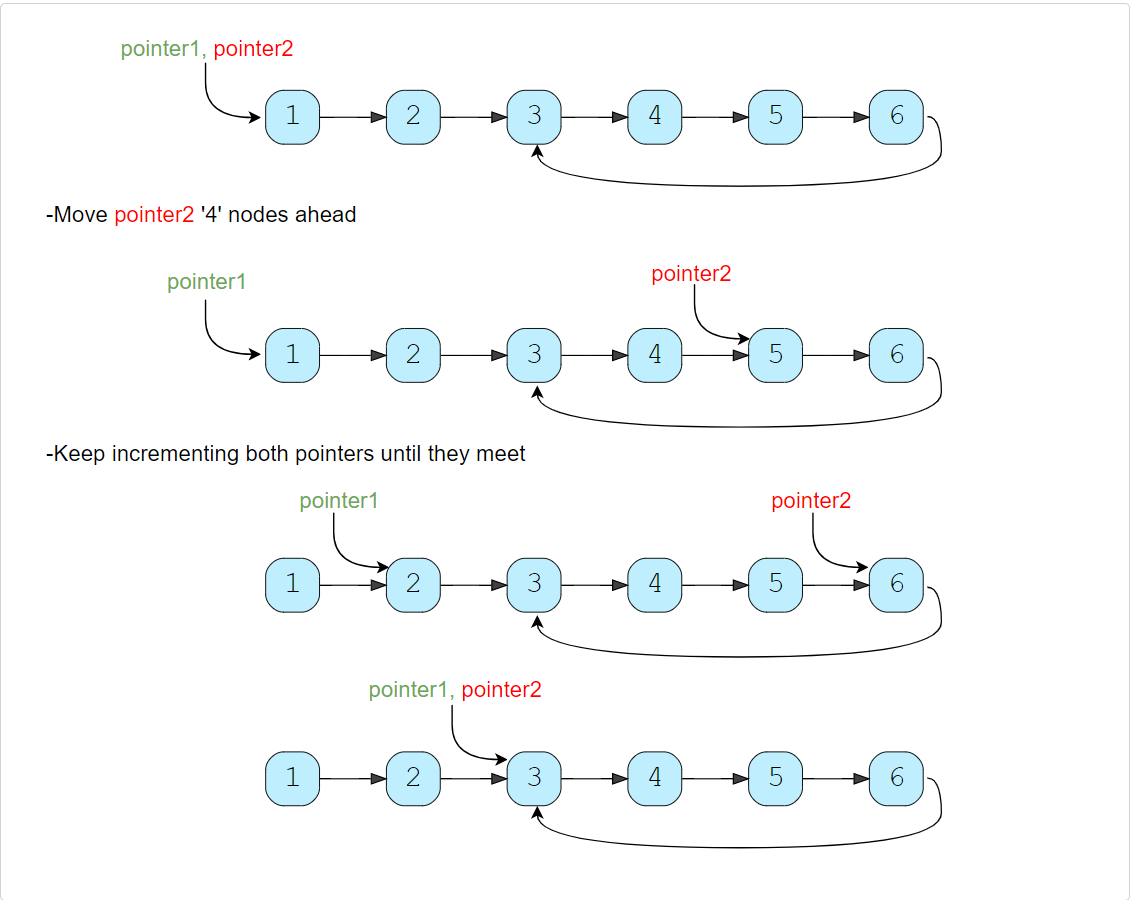
We can use the algorithm discussed in LinkedList Cycle to find the length of the cycle and then follow the above-mentioned steps to find the start of the cycle.

Code

Here is what our algorithm will look like:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
#class Node:
#  def __init__(self, value, next=None):
#    self.val = value
#    self.next = next

class Solution:
  def findCycleStart(self, head):
    cycle_length = 0

    # Find the LinkedList cycle using Floyd's Tortoise and Hare algorithm
    slow, fast = head, head
    while (fast is not None and fast.next is not None):
      fast = fast.next.next  # Move two steps at a time
      slow = slow.next       # Move one step at a time
      if slow == fast:       # Found the cycle
        cycle_length = self.calculate_cycle_length(slow)
        break

    return self.find_start(head, cycle_length)

  def calculate_cycle_length(self, slow):
    current = slow
    cycle_length = 0

    # Calculate the length of the cycle by moving through it
    while True:
      current = current.next
      cycle_length += 1
      if current == slow:  # Reached back to the starting point of the cycle
        break

    return cycle_length

  def find_start(self, head, cycle_length):
    pointer1 = head
    pointer2 = head

    # Move pointer2 ahead 'cycle_length' nodes
    while cycle_length > 0:
      pointer2 = pointer2.next
      cycle_length -= 1

    # Increment both pointers until they meet at the start of the cycle
    while pointer1 != pointer2:
      pointer1 = pointer1.next
      pointer2 = pointer2.next

    return pointer1

def main():
  sol = Solution()
  head = Node(1)
  head.next = Node(2)
  head.next.next = Node(3)
  head.next.next.next = Node(4)
  head.next.next.next.next = Node(5)
  head.next.next.next.next.next = Node(6)

  # Create a cycle by connecting nodes
  head.next.next.next.next.next.next = head.next.next
  print("LinkedList cycle start: " + str(sol.findCycleStart(head).val))

  # Create a different cycle
  head.next.next.next.next.next.next = head.next.next.next
  print("LinkedList cycle start: " + str(sol.findCycleStart(head).val))

  # Create a cycle that points back to the head
  head.next.next.next.next.next.next = head
  print("LinkedList cycle start: " + str(sol.findCycleStart(head).val))

main()

Time Complexity

As we know, finding the cycle in a LinkedList with ‘N’ nodes and also finding the length of the cycle requires O(N). Also, as we saw in the above algorithm, we will need O(N) to find the start of the cycle. Therefore, the overall time complexity of our algorithm will be O(N).

Space Complexity

The algorithm runs in constant space O(1).

Happy Number (medium)

Top Interview 150 | 202. Happy Number Design Gurus Educative.io

Problem Statement

Any number will be called a happy number if, after repeatedly replacing it with a number equal to the sum of the square of all of its digits, leads us to number ‘1’. All other (not-happy) numbers will never reach ‘1’. Instead, they will be stuck in a cycle of numbers which does not include ‘1’.

Example 1:

1
2
3
Input: 23   
Output: true (23 is a happy number)  
Explanations: Here are the steps to find out that 23 is a happy number:
  1. 2^2 + 3 ^2 = 4 + 9 = 13
  2. 1^2 + 3^2 = 1 + 9 = 10
  3. 1^2 + 0^2 = 1 + 0 = 1

Example 2:

1
2
3
Input: 12   
Output: false (12 is not a happy number)  
Explanations: Here are the steps to find out that 12 is not a happy number:
  1. 1^2 + 2 ^2 = 1 + 4 = 5
  2. 5^2 = 25
  3. 2^2 + 5^2 = 4 + 25 = 29
  4. 2^2 + 9^2 = 4 + 81 = 85
  5. 8^2 + 5^2 = 64 + 25 = 89
  6. 8^2 + 9^2 = 64 + 81 = 145
  7. 1^2 + 4^2 + 5^2 = 1 + 16 + 25 = 42
  8. 4^2 + 2^2 = 16 + 4 = 20
  9. 2^2 + 0^2 = 4 + 0 = 4
  10. 4^2 = 16
  11. 1^2 + 6^2 = 1 + 36 = 37
  12. 3^2 + 7^2 = 9 + 49 = 58
  13. 5^2 + 8^2 = 25 + 64 = 89

Step ‘13’ leads us back to step ‘5’ as the number becomes equal to ‘89’, this means that we can never reach ‘1’, therefore, ‘12’ is not a happy number.

Constraints:

  • 1 <= n <= 231 - 1

Solution

The process, defined above, to find out if a number is a happy number or not, always ends in a cycle. If the number is a happy number, the process will be stuck in a cycle on number ‘1,’ and if the number is not a happy number then the process will be stuck in a cycle with a set of numbers. As we saw in Example-2 while determining if ‘12’ is a happy number or not, our process will get stuck in a cycle with the following numbers: 89 -> 145 -> 42 -> 20 -> 4 -> 16 -> 37 -> 58 -> 89

We saw in the LinkedList Cycle problem that we can use the Fast & Slow pointers method to find a cycle among a set of elements. As we have described above, each number will definitely have a cycle. Therefore, we will use the same fast & slow pointer strategy to find the cycle and once the cycle is found, we will see if the cycle is stuck on number ‘1’ to find out if the number is happy or not.

Here is the visual representation of this algorithm for Example-2:

Code

Here is what our algorithm will look like:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution:
  def find(self, num):
    slow, fast = num, num
    while True:
      slow = self.find_square_sum(slow)  # move one step
      fast = self.find_square_sum(self.find_square_sum(fast))  # move two steps
      if slow == fast:  # found the cycle
        break
    return slow == 1  # see if the cycle is stuck on the number '1'


  def find_square_sum(self, num):
    _sum = 0
    while (num > 0):
      digit = num % 10
      _sum += digit * digit
      num //= 10
    return _sum


def main():
  sol = Solution()
  print(sol.find(23))
  print(sol.find(12))


main()

Time Complexity

The time complexity of the algorithm is difficult to determine. However we know the fact that all unhappy numbers eventually get stuck in the cycle: 4 -> 16 -> 37 -> 58 -> 89 -> 145 -> 42 -> 20 -> 4

This sequence behavior tells us two things:

  1. If the number NN is less than or equal to 1000, then we reach the cycle or ‘1’ in at most 1001 steps.
  2. For N > 1000, suppose the number has ‘M’ digits and the next number is ‘N1’. From the above Wikipedia link, we know that the sum of the squares of the digits of ‘N’ is at most $9^2M$, or $81M$ (this will happen when all digits of ‘N’ are ‘9’).

This means:

  1. $N1 < 81M$
  2. As we know $M = log(N+1)$
  3. Therefore: $N1 < 81 * log(N+1) => N1 = O(logN)$

This concludes that the above algorithm will have a time complexity of O(logN).

Space Complexity

The algorithm runs in constant space O(1).

Middle of the LinkedList (easy)

876. Middle of the Linked List Design Gurus Educative.io

Problem Statement

Given the head of a Singly LinkedList, write a method to return the middle node of the LinkedList.

If the total number of nodes in the LinkedList is even, return the second middle node.

Example 1:

1
2
Input: 1 -> 2 -> 3 -> 4 -> 5 -> null
Output: 3

Example 2:

1
2
Input: 1 -> 2 -> 3 -> 4 -> 5 -> 6 -> null
Output: 4

Example 3:

1
2
Input: 1 -> 2 -> 3 -> 4 -> 5 -> 6 -> 7 -> null
Output: 4

Constraints:

  • The number of nodes in the list is in the range [1, 100].
  • 1 <= Node.val <= 100

Solution

One brute force strategy could be to first count the number of nodes in the LinkedList and then find the middle node in the second iteration. Can we do this in one iteration?

We can use the Fast & Slow pointers method such that the fast pointer is always twice the nodes ahead of the slow pointer. This way, when the fast pointer reaches the end of the LinkedList, the slow pointer will be pointing at the middle node.

let’s visualize example 3 via the below diagram.

Code

Here is what our algorithm will look like:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
#class Node:
#  def __init__(self, value, next=None):
#    self.val = value
#    self.next = next

# Function to find the middle of a linked list
def findMiddle(head):
  slow = head
  fast = head
  
  # Traverse the linked list with two pointers (slow and fast)
  # until the fast pointer reaches the end or goes one step further
  while (fast is not None and fast.next is not None):
    slow = slow.next
    fast = fast.next.next

  # Return the node pointed to by the slow pointer, which is the middle
  return slow

# Main function to test the findMiddle function
def main():
  head = Node(1)
  head.next = Node(2)
  head.next.next = Node(3)
  head.next.next.next = Node(4)
  head.next.next.next.next = Node(5)

  # Print the middle node's value
  print("Middle Node: " + str(findMiddle(head).val))

  head.next.next.next.next.next = Node(6)
  # Print the middle node's value after adding a new node
  print("Middle Node: " + str(findMiddle(head).val))

  head.next.next.next.next.next.next = Node(7)
  # Print the middle node's value after adding another new node
  print("Middle Node: " + str(findMiddle(head).val))

# Call the main function to execute the code
main()

Time complexity

The above algorithm will have a time complexity of O(N) where ‘N’ is the number of nodes in the LinkedList.

Space complexity

The algorithm runs in constant space O(1).

Problem Challenge 1

234. Palindrome Linked List Design Gurus Educative.io

Palindrome LinkedList (medium)

Given the head of a Singly LinkedList, write a method to check if the LinkedList is a palindrome or not.

Your algorithm should use constant space and the input LinkedList should be in the original form once the algorithm is finished. The algorithm should have O(N)O(N) time complexity where ‘N’ is the number of nodes in the LinkedList.

Example 1:

1
2
Input: 2 -> 4 -> 6 -> 4 -> 2 -> null
Output: true

Example 2:

1
2
Input: 2 -> 4 -> 6 -> 4 -> 2 -> 2 -> null
Output: false

Constraints:

  • The number of nodes in the list is in the range [1, 10<sup>5</sup>].
  • 0 <= Node.val <= 9

  1. Solution

    As we know, a palindrome LinkedList will have nodes values that read the same backward or forward. This means that if we divide the LinkedList into two halves, the node values of the first half in the forward direction should be similar to the node values of the second half in the backward direction. As we have been given a Singly LinkedList, we can’t move in the backward direction. To handle this, we will perform the following steps:

    1. We can use the Fast & Slow pointers method similar to Middle of the LinkedList to find the middle node of the LinkedList.
    2. Once we have the middle of the LinkedList, we will reverse the second half.
    3. Then, we will compare the first half with the reversed second half to see if the LinkedList represents a palindrome.
    4. Finally, we will reverse the second half of the LinkedList again to revert and bring the LinkedList back to its original form.

    Here is the visual representation of this algorithm for Example-2:

Code

Here is what our algorithm will look like:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
#class Node:
#  def __init__(self, value, next=None):
#    self.val = value
#    self.next = next


class Solution:
  def isPalindrome(self, head):
    if head is None or head.next is None:
      return True

    # find middle of the LinkedList
    slow, fast = head, head
    while (fast is not None and fast.next is not None):
      slow = slow.next
      fast = fast.next.next

    head_second_half = self.reverse(slow)  # reverse the second half
    # store the head of reversed part to revert back later
    copy_head_second_half = head_second_half

    # compare the first and the second half
    while (head is not None and head_second_half is not None):
      if head.val != head_second_half.val:
        break  # not a palindrome

      head = head.next
      head_second_half = head_second_half.next

    self.reverse(copy_head_second_half)  # revert the reverse of the second half

    if head is None or head_second_half is None:  # if both halves match
      return True

    return False


  def reverse(self, head):
    prev = None
    while (head is not None):
      next = head.next
      head.next = prev
      prev = head
      head = next
    return prev


def main():
  sol = Solution()
  head = Node(2)
  head.next = Node(4)
  head.next.next = Node(6)
  head.next.next.next = Node(4)
  head.next.next.next.next = Node(2)

  print("Is palindrome: " + str(sol.isPalindrome(head)))

  head.next.next.next.next.next = Node(2)
  print("Is palindrome: " + str(sol.isPalindrome(head)))


main()

Time complexity

The above algorithm will have a time complexity of O(N) where ‘N’ is the number of nodes in the LinkedList.

Space complexity

The algorithm runs in constant space O(1).

# Problem Challenge 2

143. Reorder List Design Gurus Educative.io

Rearrange a LinkedList (medium)

Given the head of a Singly LinkedList, write a method to modify the LinkedList such that the nodes from the second half of the LinkedList are inserted alternately to the nodes from the first half in reverse order. So if the LinkedList has nodes 1 -> 2 -> 3 -> 4 -> 5 -> 6 -> null, your method should return 1 -> 6 -> 2 -> 5 -> 3 -> 4 -> null.

Your algorithm should not use any extra space and the input LinkedList should be modified in-place.

Example 1:

1
2
Input: 2 -> 4 -> 6 -> 8 -> 10 -> 12 -> null
Output: 2 -> 12 -> 4 -> 10 -> 6 -> 8 -> null

Example 2:

1
2
Input: 2 -> 4 -> 6 -> 8 -> 10 -> null
Output: 2 -> 10 -> 4 -> 8 -> 6 -> null

Constraints:

  • The number of nodes in the list is in the range [1, 5 * 10^4].
  • 1 <= Node.val <= 1000

Solution

This problem shares similarities with Palindrome LinkedList. To rearrange the given LinkedList we will follow the following steps:

  1. We can use the Fast & Slow pointers method similar to Middle of the LinkedList to find the middle node of the LinkedList.
  2. Once we have the middle of the LinkedList, we will reverse the second half of the LinkedList.
  3. Finally, we’ll iterate through the first half and the reversed second half to produce a LinkedList in the required order.

Here is the visual representation of this algorithm for Example-1:

Code

Here is what our algorithm will look like:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
#class Node:
#  def __init__(self, value, next=None):
#    self.val = value
#    self.next = next

class Solution:
  def reorder(self, head):
    if head is None or head.next is None:
      return head

    # find middle of the LinkedList
    slow, fast = head, head
    while fast is not None and fast.next is not None:
      slow = slow.next
      fast = fast.next.next

    # slow is now pointing to the middle node
    head_second_half = self.reverse(slow)  # reverse the second half
    head_first_half = head

    # rearrange to produce the LinkedList in the required order
    while head_first_half is not None and head_second_half is not None:
      temp = head_first_half.next
      head_first_half.next = head_second_half
      head_first_half = temp

      temp = head_second_half.next
      head_second_half.next = head_first_half
      head_second_half = temp

    # set the next of the last node to 'None'
    if head_first_half is not None:
      head_first_half.next = None
    return head


  def reverse(self, head):
    prev = None
    while head is not None:
      next = head.next
      head.next = prev
      prev = head
      head = next
    return prev

  def print_list(self, head):
    temp = head
    while temp is not None:
      print(str(temp.val) + " ", end='')
      temp = temp.next
    print()


def main():
  sol = Solution()
  head = Node(2)
  head.next = Node(4)
  head.next.next = Node(6)
  head.next.next.next = Node(8)
  head.next.next.next.next = Node(10)
  head.next.next.next.next.next = Node(12)
  sol.reorder(head)
  sol.print_list(head)


main()

Time Complexity

The above algorithm will have a time complexity of O(N) where ‘N’ is the number of nodes in the LinkedList.

Space Complexity

The algorithm runs in constant space O(1).

#Problem Challenge 3

457. Circular Array Loop Design Gurus Educative.io

Cycle in a Circular Array (hard)

We are given an array containing positive and negative numbers. Suppose the array contains a number ‘M’ at a particular index. Now, if ‘M’ is positive we will move forward ‘M’ indices and if ‘M’ is negative move backwards ‘M’ indices. You should assume that the array is circular which means two things:

  1. If, while moving forward, we reach the end of the array, we will jump to the first element to continue the movement.
  2. If, while moving backward, we reach the beginning of the array, we will jump to the last element to continue the movement.

Write a method to determine if the array has a cycle. The cycle should have more than one element and should follow one direction which means the cycle should not contain both forward and backward movements.

Example 1:

1
2
3
Input: [1, 2, -1, 2, 2]
Output: true
Explanation: The array has a cycle among indices: 0 -> 1 -> 3 -> 0

Example 2:

1
2
3
Input: [2, 2, -1, 2]
Output: true
Explanation: The array has a cycle among indices: 1 -> 3 -> 1

Example 3:

1
2
3
Input: [2, 1, -1, -2]
Output: false
Explanation: The array does not have any cycle.

Constraints:

  • 1 <= nums.length <= 5000
  • `-1000 <= nums[i] <= 1000
  • nums[i] != 0

Solution

This problem involves finding a cycle in the array and, as we know, the Fast & Slow pointer method is an efficient way to do that. We can start from each index of the array to find the cycle. If a number does not have a cycle we will move forward to the next element. There are a couple of additional things we need to take care of:

  1. As mentioned in the problem, the cycle should have more than one element. This means that when we move a pointer forward, if the pointer points to the same element after the move, we have a one-element cycle. Therefore, we can finish our cycle search for the current element.
  2. The other requirement mentioned in the problem is that the cycle should not contain both forward and backward movements. We will handle this by remembering the direction of each element while searching for the cycle. If the number is positive, the direction will be forward and if the number is negative, the direction will be backward. So whenever we move a pointer forward, if there is a change in the direction, we will finish our cycle search right there for the current element.

Here is the visual representation of this algorithm for Example-1:

Code

Here is what our algorithm will look like:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
class Solution:
  def loopExists(self, arr):
    for i in range(len(arr)):
      is_forward = arr[i] >= 0  # if we are moving forward or not
      slow, fast = i, i

      # if slow or fast becomes '-1' this means we can't find cycle for this number
      while True:
        # move one step for slow pointer
        slow = self.find_next_index(arr, is_forward, slow)
        # move one step for fast pointer
        fast = self.find_next_index(arr, is_forward, fast)
        if (fast != -1):
          # move another step for fast pointer
          fast = self.find_next_index(arr, is_forward, fast)
        if slow == -1 or fast == -1 or slow == fast:
          break

      if slow != -1 and slow == fast:
        return True

    return False


  def find_next_index(self, arr, is_forward, current_index):
    direction = arr[current_index] >= 0

    if is_forward != direction:
      return -1  # change in direction, return -1

    next_index = (current_index + arr[current_index]) % len(arr)

    # one element cycle, return -1
    if next_index == current_index:
      next_index = -1

    return next_index


def main():
  sol = Solution()
  print(sol.loopExists([1, 2, -1, 2, 2]))
  print(sol.loopExists([2, 2, -1, 2]))
  print(sol.loopExists([2, 1, -1, -2]))


main()

Time Complexity

The above algorithm will have a time complexity of O(N^2) where ‘N’ is the number of elements in the array. This complexity is due to the fact that we are iterating all elements of the array and trying to find a cycle for each element.

Space Complexity

The algorithm runs in constant space O(1).

An Alternate Approach

In our algorithm, we don’t keep a record of all the numbers that have been evaluated for cycles. We know that all such numbers will not produce a cycle for any other instance as well. If we can remember all the numbers that have been visited, our algorithm will improve to O(N) as, then, each number will be evaluated for cycles only once. We can keep track of this by creating a separate array however the space complexity of our algorithm will increase to O(N).

Author：Hasuer

Link：https://hasuer.github.io/2-pattern-fast-slow-pointers/index.html

Publish date：May 2nd 2024, 12:36:30 am

Update date：May 28th 2024, 11:27:22 am

License：本文采用知识共享署名-非商业性使用 4.0 国际许可协议进行许可

CATALOG
  1. 1. Introduction
  2. 2. LinkedList Cycle (easy)
    1. 2.1. Problem Statement
    2. 2.2. Solution
    3. 2.3. Code
      1. 2.3.1. Time Complexity
      2. 2.3.2. Space Complexity
    4. 2.4. Similar Problems
  3. 3. Start of LinkedList Cycle (medium)
    1. 3.1. Problem Statement
    2. 3.2. Solution
      1. 3.2.1. Code
      2. 3.2.2. Time Complexity
      3. 3.2.3. Space Complexity
  4. 4. Happy Number (medium)
    1. 4.1. Problem Statement
    2. 4.2. Solution
    3. 4.3. Code
      1. 4.3.1. Time Complexity
      2. 4.3.2. Space Complexity
  5. 5. Middle of the LinkedList (easy)
    1. 5.1. Problem Statement
    2. 5.2. Solution
    3. 5.3. Code
      1. 5.3.1. Time complexity
      2. 5.3.2. Space complexity
  6. 6. Problem Challenge 1
    1. 6.1. Palindrome LinkedList (medium)
    2. 6.2. Code
      1. 6.2.1. Time complexity
      2. 6.2.2. Space complexity
  7. 7. # Problem Challenge 2
    1. 7.1. Rearrange a LinkedList (medium)
    2. 7.2. Solution
    3. 7.3. Code
      1. 7.3.1. Time Complexity
      2. 7.3.2. Space Complexity
  8. 8. #Problem Challenge 3
    1. 8.1. Cycle in a Circular Array (hard)
    2. 8.2. Solution
    3. 8.3. Code
      1. 8.3.1. Time Complexity
      2. 8.3.2. Space Complexity
      3. 8.3.3. An Alternate Approach
Total : 41
2024
2022
2021
Interview
技术笔记 Grokking-Interview-Pattern