Hasuer's Studio.

13. Pattern Island (Matrix traversal)

Grokking Interview Pattern Interview
Word count: 7.8kReading time: 48 min
2024/05/13

Introduction to Island Pattern

Many coding interview problems involve traversing 2D arrays (aka matrix or grid). The Island pattern describes all the efficient ways to traverse a matrix. This pattern will go through many problems to explain matrix traversal using Depth First Search (DFS) and Breadth First Search (BFS) approaches and their variants.

Let’s jump onto our first problem to develop an understanding of this pattern.

Number of Islands

Top Interview 150 | 200. Number of Islands Design Gurus

Problem Statement

Given a 2D array (i.e., a matrix) containing only 1s (land) and 0s (water), count the number of islands in it.

An island is a connected set of 1s (land) and is surrounded by either an edge or 0s (water). Each cell is considered connected to other cells horizontally or vertically (not diagonally).

Example 1

Input: matrix =

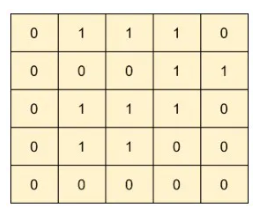
Output: 1
Explanation: The matrix has only one island. See the highlighted cells below.

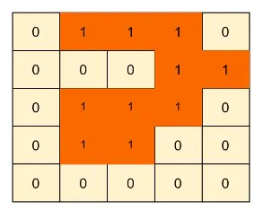
Example 2

Input: matrix =

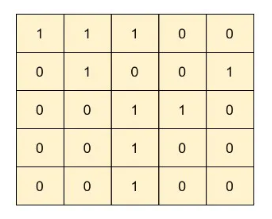
Output: 3
Explanation: The matrix has three islands. See the highlighted cells below.

Constraints:

  • m == matrix.length
  • n == matrix[i].length
  • 1 <= m, n <= 300
  • matrix[i][j] is '0' or '1'.

Solution

We can traverse the matrix linearly to find islands.

Whenever we find a cell with the value ‘1’ (i.e., land), we have found an island. Using that cell as the root node, we will perform a Depth First Search (DFS) or Breadth First Search (BFS) to find all of its connected land cells. During our DFS or BFS traversal, we will find and mark all the horizontally and vertically connected land cells.

We need to have a mechanism to mark each land cell to ensure that each land cell is visited only once. To mark a cell visited, we have two options:

  1. We can update the given input matrix. Whenever we see a ‘1’, we will make it ‘0’.
  2. A separate boolean matrix can be used to record whether or not each cell has been visited.

Following is the DFS or BFS traversal of the example-2 mentioned above:

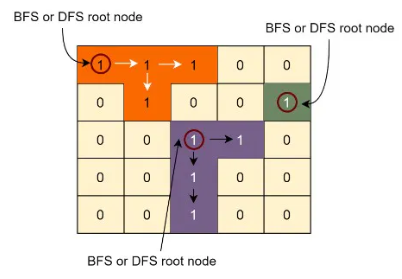
By following the above algorithm, every time DFS or BFS is triggered, we are sure that we have found an island. We will keep a running count to calculate the total number of islands.

Below, we will see three solutions based on:

  1. DFS
  2. BFS
  3. BFS with visited matrix

Code (DFS)

Here is what our DFS algorithm will look like. We will update the input matrix to mark cells visited.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
# dfs一般使用stack或者递归
class Solution:
  def countIslands(self, matrix):
      rows = len(matrix)
      cols = len(matrix[0])
      totalIslands = 0

      for i in range(rows):
          for j in range(cols):
              if (matrix[i][j] == 1):  # only if the cell is a land
                  # we have found an island
                  totalIslands += 1
                  self.visit_is_land_DFS(matrix, i, j)
      return totalIslands


  def visit_is_land_DFS(self, matrix,  x,  y):
      if (x < 0 or x >= len(matrix) or y < 0 or y >= len(matrix[0])):
          return  # return, if it is not a valid cell
      if (matrix[x][y] == 0):
          return  # return, if it is a water cell

      matrix[x][y] = 0  # mark the cell visited by making it a water cell

      # recursively visit all neighboring cells (horizontally & vertically)
      self.visit_is_land_DFS(matrix, x + 1, y)  # lower cell
      self.visit_is_land_DFS(matrix, x - 1, y)  # upper cell
      self.visit_is_land_DFS(matrix, x, y + 1)  # right cell
      self.visit_is_land_DFS(matrix, x, y - 1)  # left cell


def main():
  sol = Solution()
  print(sol.countIslands([[0, 1, 1, 1, 0], [0, 0, 0, 1, 1], [
        0, 1, 1, 1, 0], [0, 1, 1, 0, 0], [0, 0, 0, 0, 0]]))
  print(sol.countIslands([[1, 1, 1, 0, 0], [0, 1, 0, 0, 1], [
        0, 0, 1, 1, 0], [0, 0, 1, 0, 0], [0, 0, 1, 0, 0]]))


main()

Time Complexity
Time complexity of the above algorithm will be O(M \ N)*, where ‘M’ is the number of rows and ‘N’ is the number of columns of the input matrix. This is due to the fact that we have to traverse the whole matrix to find the islands.

Space Complexity
DFS recursion stack can go O(M \ N)* deep when the whole matrix is filled with ‘1’s. Hence, the space complexity will be O(M \ N)* , where ‘M’ is the number of rows and ‘N’ is the number of columns of the input matrix.

Code (DFS) (DFS with visited matrix)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
# 过leetcode
from collections import deque


class Solution:
    def countIslands(self, matrix):
        rows = len(matrix)
        cols = len(matrix[0])
        totalIslands = 0
        visited = [[False for i in range(cols)] for j in range(rows)]

        for i in range(rows):
            for j in range(cols):
                if (matrix[i][j] == 1 and not visited[i][j]):  # only if the cell is a land
                    # we have found an island
                    totalIslands += 1
                    self.visit_is_land_DFS(matrix, visited, i, j)
        return totalIslands

    def visit_is_land_DFS(self, matrix, visited, x, y):
        stack = deque()
        stack.append((x, y))
        # stack = deque([(x, y)]) # 这一行可以代替上面两行
        while stack:
            x, y = stack.pop()
            if (x < 0 or x >= len(matrix) or y < 0 or y >= len(matrix[0])):
                continue  # continue, if it is not a valid cell
            if (visited[x][y] or matrix[x][y] == 0):
                continue  # continue if the cell is water or visited

            visited[x][y] = True  # mark the cell visited by making it a water cell

            # recursively visit all neighboring cells (horizontally & vertically)
            stack.append((x + 1, y))  # lower cell
            stack.append((x - 1, y))  # upper cell
            stack.append((x, y + 1))  # right cell
            stack.append((x, y - 1))  # left cell


def main():
    sol = Solution()
    print(sol.countIslands([[0, 1, 1, 1, 0], [0, 0, 0, 1, 1], [
        0, 1, 1, 1, 0], [0, 1, 1, 0, 0], [0, 0, 0, 0, 0]]))
    print(sol.countIslands([[1, 1, 1, 0, 0], [0, 1, 0, 0, 1], [
        0, 0, 1, 1, 0], [0, 0, 1, 0, 0], [0, 0, 1, 0, 0]]))


main()

Code (BFS)

Here is what our BFS algorithm will look like. We will update the input matrix to mark cells visited.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
# BFS一般使用queue,很少见递归
from collections import deque


class Solution:
  def count_is_lands_BFS(self, matrix):
      rows = len(matrix)
      cols = len(matrix[0])
      totalIslands = 0

      for i in range(rows):
          for j in range(cols):
              if (matrix[i][j] == 1):  # only if the cell is a land
                  # we have found an island
                  totalIslands += 1
                  self.visit_is_land_BFS(matrix, i, j)
      return totalIslands


  def visit_is_land_BFS(self, matrix,  x,  y):
      neighbors = deque([(x, y)])
      while neighbors:
          row, col = neighbors.popleft()

          if row < 0 or row >= len(matrix) or col < 0 or col >= len(matrix[0]):
              continue  # continue, if it is not a valid cell
          if matrix[row][col] == 0:
              continue  # continue if it is a water cell

          matrix[row][col] = 0  # mark the cell visited by making it a water cell

          # insert all neighboring cells to the queue for BFS
          # append元素，entend列表
          neighbors.extend([(row + 1, col)])  # lower cell
          neighbors.extend([(row - 1, col)])  # upper cell
          neighbors.extend([(row, col + 1)])  # right cell
          neighbors.extend([(row, col - 1)])  # left cell


def main():
  sol = Solution()
  print(sol.count_is_lands_BFS([[0, 1, 1, 1, 0], [0, 0, 0, 1, 1], [
        0, 1, 1, 1, 0], [0, 1, 1, 0, 0], [0, 0, 0, 0, 0]]))
  print(sol.count_is_lands_BFS([[1, 1, 1, 0, 0], [0, 1, 0, 0, 1], [
        0, 0, 1, 1, 0], [0, 0, 1, 0, 0], [0, 0, 1, 0, 0]]))


main()

Time Complexity
Time complexity of the above algorithm will be O(M * N), where ‘M’ is the number of rows and ‘N’ is the number of columns.

Space Complexity
Space complexity of the above algorithm will be *O(min(M, N)). In the worst case, when the matrix is completely filled with land cells, the size of the queue can grow up to min(M, N).

Code (BFS with visited matrix)

Here is what our BFS algorithm will look like. We will keep a separate boolean matrix to record whether or not each cell has been visited.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
from collections import deque


class Solution:
  def count_is_lands_BFS(self, matrix):
      rows = len(matrix)
      cols = len(matrix[0])
      totalIslands = 0
      visited = [[False for i in range(cols)] for j in range(rows)]

      for i in range(rows):
          for j in range(cols):
              # if the cell has not been visited before and is a land
              if (matrix[i][j] == 1 and not visited[i][j]):
                  # we have found an island
                  totalIslands += 1
                  self.visit_is_land_BFS(matrix, visited, i, j)
      return totalIslands


  def visit_is_land_BFS(self, matrix, visited, x,  y):
      neighbors = deque([(x, y)])
      while neighbors:
          row, col = neighbors.popleft()

          if row < 0 or row >= len(matrix) or col < 0 or col >= len(matrix[0]):
              continue  # continue, if it is not a valid cell
          if matrix[row][col] == 0 or visited[row][col]:
              continue  # continue if the cell is water or visited

          visited[row][col] = True # mark the visited array

          # insert all neighboring cells to the queue for BFS
          # append元素，entend列表
          neighbors.extend([(row + 1, col)])  # lower cell
          neighbors.extend([(row - 1, col)])  # upper cell
          neighbors.extend([(row, col + 1)])  # right cell
          neighbors.extend([(row, col - 1)])  # left cell


def main():
  sol = Solution()
  print(sol.count_is_lands_BFS([[0, 1, 1, 1, 0], [0, 0, 0, 1, 1], [
        0, 1, 1, 1, 0], [0, 1, 1, 0, 0], [0, 0, 0, 0, 0]]))
  print(sol.count_is_lands_BFS([[1, 1, 1, 0, 0], [0, 1, 0, 0, 1], [
        0, 0, 1, 1, 0], [0, 0, 1, 0, 0], [0, 0, 1, 0, 0]]))


main()

Time Complexity
Time complexity of the above algorithm will be O(M \ N)*, where ‘M’ is the number of rows and ‘N’ is the number of columns.

Space Complexity
Because of the visited array and max size of the queue, the space complexity will be O(M \ N)*, where ‘M’ is the number of rows and ‘N’ is the number of columns of the input matrix.

Biggest Island

695. Max Area of Island Design Gurus

Problem Statement

Given a 2D array (i.e., a matrix) containing only 1s (land) and 0s (water), find the biggest island in it. Write a function to return the area of the biggest island.

An island is a connected set of 1s (land) and is surrounded by either an edge or 0s (water). Each cell is considered connected to other cells horizontally or vertically (not diagonally).

Example 1

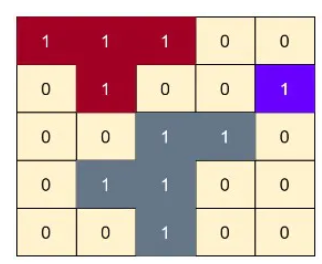
Input: matrix =

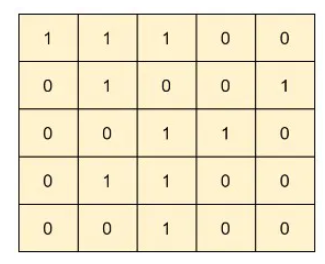
Output: 5
Explanation: The matrix has three islands. The biggest island has 5 cells .

Constraints:

  • m == matrix.length
  • n == matrix[i].length
  • 1 <= m, n <= 50
  • matrix[i][j] is '0' or '1'.

Solution

The question follows the Island pattern and is quite similar to Number of Islands problem.

We will traverse the matrix linearly to find islands.

Whenever we find a cell with the value ‘1’ (i.e., land), we have found an island. Using that cell as the root node, we will perform a Depth First Search (DFS) or Breadth First Search (BFS) to find all of its connected land cells. During our DFS or BFS traversal, we will find and mark all the horizontally and vertically connected land cells.

We will keep a variable to remember the max area of any island.

Algorithm Walkthrough

Here is the detailed walkthrough of the DFS algorithm:

  1. We first initialize biggestIslandArea to 0. This variable will keep track of the largest island’s area we have encountered so far.
  2. Then, we traverse each cell in the matrix. If the cell’s value is 1 (land), we begin a DFS search from this cell using the visitIslandDFS function. This function will visit the cell and all its neighboring cells that are part of the same island.
  3. In the visitIslandDFS function, we first check if the current cell (x, y) is within the boundaries of the matrix and if it’s a land cell. If it’s not, we return 0.
  4. We then mark the current cell as visited by setting its value to 0 (water). This helps avoid visiting the same cell again and ending up in an infinite loop.
  5. We initialize the area of the current island to 1 (counting the current cell), and then add to it the areas returned by the recursive DFS calls for the neighboring cells (top, bottom, left, and right).
  6. After we finish the DFS for a cell (meaning we have visited all cells in the island that the cell is a part of), we update biggestIslandArea with the maximum of its current value and the area of the island we just finished exploring.
  7. Finally, after traversing all cells in the matrix, we return biggestIslandArea, which now holds the area of the largest island.

Here is the visual representation of the algorithm:

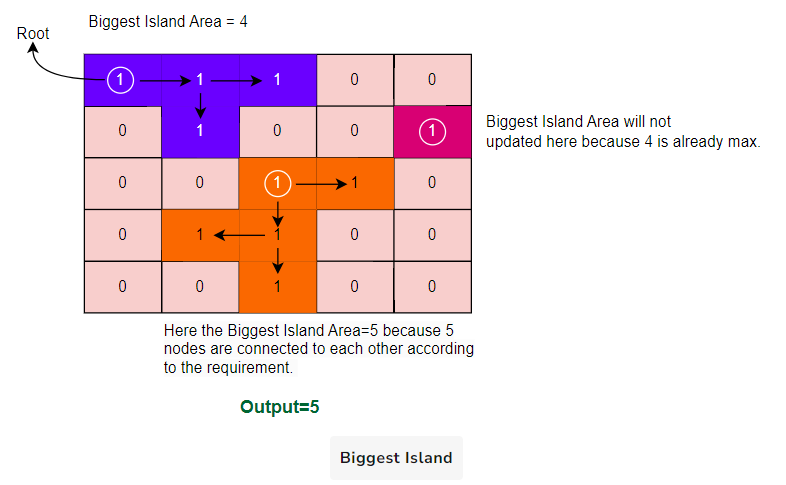
Code (DFS)

Here is what our DFS algorithm will look like. We will update the input matrix to mark nodes visited.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
# 官方使用的是DFS的递归，但是我比较习惯使用while
class Solution:
  def maxAreaOfIsland(self, matrix):
      rows = len(matrix)
      cols = len(matrix[0])
      biggestIslandArea = 0

      for i in range(rows):
          for j in range(cols):
              if (matrix[i][j] == 1):  # only if the cell is a land
                  # we have found an island
                  biggestIslandArea = max(
                      biggestIslandArea, self.visit_is_land_DFS(matrix, i, j))

      return biggestIslandArea


  def visit_is_land_DFS(self, matrix,  x,  y):
      if (x < 0 or x >= len(matrix) or y < 0 or y >= len(matrix[0])):
          return 0  # return, if it is not a valid cell
      if (matrix[x][y] == 0):
          return 0  # return, if it is a water cell

      matrix[x][y] = 0  # mark the cell visited by making it a water cell

      area = 1 # counting the current cell
      # recursively visit all neighboring cells (horizontally & vertically)
      area += self.visit_is_land_DFS(matrix, x + 1, y)  # lower cell
      area += self.visit_is_land_DFS(matrix, x - 1, y)  # upper cell
      area += self.visit_is_land_DFS(matrix, x, y + 1)  # right cell
      area += self.visit_is_land_DFS(matrix, x, y - 1)  # left cell
      return area


def main():
  sol = Solution()
  print(sol.maxAreaOfIsland([[1, 1, 1, 0, 0], [0, 1, 0, 0, 1], [
        0, 0, 1, 1, 0], [0, 1, 1, 0, 0], [0, 0, 1, 0, 0]]))

main()


# 自己实现的DFS的while版本, 过了leetcode
from collections import deque


class Solution:
    def maxAreaOfIsland(self, matrix):
        rows = len(matrix)
        cols = len(matrix[0])
        biggestIslandArea = 0
        visited = [[False for i in range(cols)] for j in range(rows)]
        for i in range(rows):
            for j in range(cols):
                if (matrix[i][j] == 1):  # only if the cell is a land
                    # we have found an island
                    biggestIslandArea = max(
                        biggestIslandArea, self.visit_is_land_DFS(matrix, visited, i, j))

        return biggestIslandArea

    def visit_is_land_DFS(self, matrix, visited, x, y):
        stack = deque([(x, y)])
        area = 0
        while stack:
            x, y = stack.pop()
            if x < 0 or x >= len(matrix) or y < 0 or y >= len(matrix[0]):
                continue  # return, if it is not a valid cell
            if matrix[x][y] == 0 or visited[x][y]:
                continue  # return, if it is a water cell

            area += 1
            visited[x][y] = True  # mark the cell visited by making it a water cell
            # recursively visit all neighboring cells (horizontally & vertically)
            stack.append((x + 1, y))  # lower cell
            stack.append((x - 1, y))  # upper cell
            stack.append((x, y + 1))  # right cell
            stack.append((x, y - 1))  # left cell
        return area


def main():
    sol = Solution()
    print(sol.maxAreaOfIsland([[1, 1, 1, 0, 0], [0, 1, 0, 0, 1], [
        0, 0, 1, 1, 0], [0, 1, 1, 0, 0], [0, 0, 1, 0, 0]]))


main()

Complexity Analysis

Time Complexity
Time complexity of the above algorithm will be O(M * N), where ‘M’ is the number of rows and ‘N’ is the number of columns of the input matrix. This is due to the fact that we have to traverse the whole matrix to find islands.

Space Complexity
DFS recursion stack can go O(M * N) deep when the whole matrix is filled with ‘1’s. Hence, the space complexity will be O(M * N), where ‘M’ is the number of rows and ‘N’ is the number of columns of the input matrix.

Flood Fill

733. Flood Fill Design Gurus

Problem Statement

Any image can be represented by a 2D integer array (i.e., a matrix) where each cell represents the pixel value of the image.

Flood fill algorithm takes a starting cell (i.e., a pixel) and a color. The given color is applied to all horizontally and vertically connected cells with the same color as that of the starting cell. Recursively, the algorithm fills cells with the new color until it encounters a cell with a different color than the starting cell.

Given a matrix, a starting cell, and a color, flood fill the matrix.

Example 1:

Input: matrix =

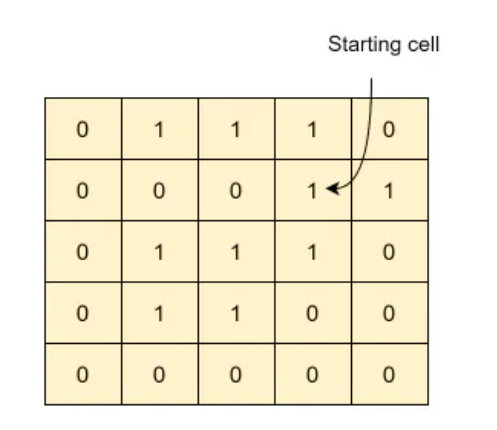
starting cell = (1, 3)
new color = 2

Output:

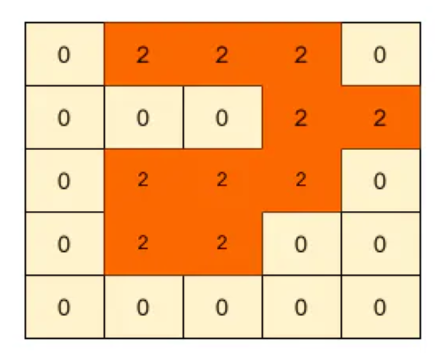
Example 2:

Input: matrix =

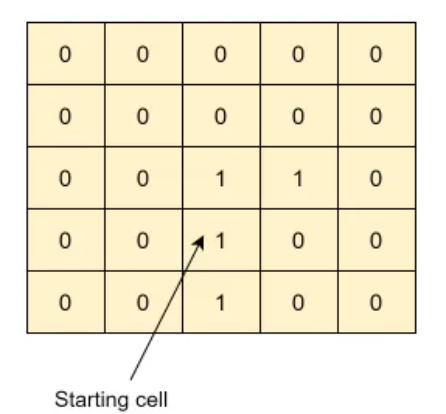
starting cell = (3, 2)

new color = 5

Output:

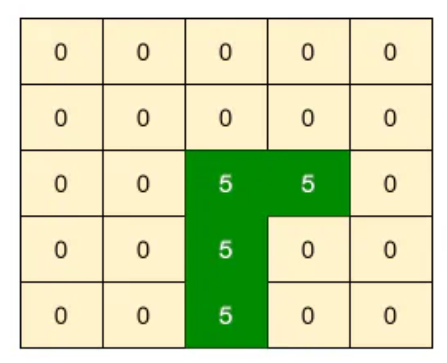
Constraints:

  • m == matrix.length
  • n == - m == matrix[i].length
  • 1 <= m, n <= 50
  • 0 <= - m == matrix[i][j], color < 216
  • 0 <= x < m
  • 0 <= y < n

Solution

The question follows the Island pattern and is quite similar to Number of Islands problem.

From the given starting cell, we can perform a Depth First Search (DFS) or Breadth First Search (BFS) to find all of its connected cells with the same color. During our DFS or BFS traversal, we will update the cells with the new color.

Following is the DFS or BFS traversal of the example-2 mentioned above:

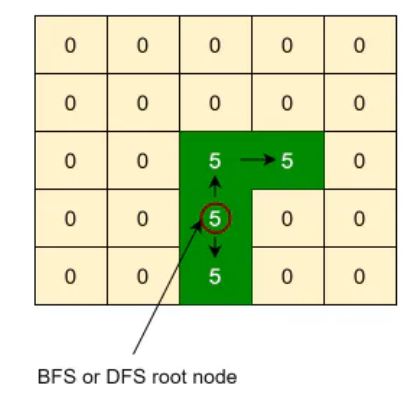
Code (DFS)

Here is what our DFS algorithm will look like:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
# 官方使用的是DFS的递归，但是我比较习惯使用while
class Solution:
  def floodFill(self, matrix, x, y, newColor):
      if matrix[x][y] != newColor:
          self.fill_DFS(matrix, x, y, matrix[x][y], newColor)
      return matrix


  def fill_DFS(self, matrix,  x,  y, oldColor, newColor):
      if x < 0 or x >= len(matrix) or y < 0 or y >= len(matrix[0]):
          return  # return, if it is not a valid cell
      if matrix[x][y] != oldColor:
          return  # return, if it is not the required color

      matrix[x][y] = newColor  # // update the cell to the new color

      # recursively visit all neighboring cells (horizontally & vertically)
      self.fill_DFS(matrix, x + 1, y, oldColor, newColor)  # lower cell
      self.fill_DFS(matrix, x - 1, y, oldColor, newColor)  # upper cell
      self.fill_DFS(matrix, x, y + 1, oldColor, newColor)  # right cell
      self.fill_DFS(matrix, x, y - 1, oldColor, newColor)  # left cell


def main():
  sol = Solution()
  print(sol.floodFill([[0, 1, 1, 1, 0], [0, 0, 0, 1, 1], [
        0, 1, 1, 1, 0], [0, 1, 1, 0, 0], [0, 0, 0, 0, 0]], 1, 3, 2))
  print(sol.floodFill([[0, 0, 0, 0, 0], [0, 0, 0, 0, 0], [
        0, 0, 1, 1, 0], [0, 0, 1, 0, 0], [0, 0, 1, 0, 0]], 3, 2, 5))


main()

# 自己实现的DFS while, 过了leetcode
from collections import deque


class Solution:
    def floodFill(self, matrix, x, y, newColor):
        if matrix[x][y] != newColor:
            self.fill_DFS(matrix, x, y, matrix[x][y], newColor)
        return matrix

    def fill_DFS(self, matrix, x, y, oldColor, newColor):
        stack = deque([(x, y)])
        while stack:
            x, y = stack.pop()
            if x < 0 or x >= len(matrix) or y < 0 or y >= len(matrix[0]):
                continue  # continue, if it is not a valid cell
            if matrix[x][y] != oldColor:
                continue  # continue, if it is not the required color

            matrix[x][y] = newColor  # // update the cell to the new color

            # recursively visit all neighboring cells (horizontally & vertically)
            stack.append((x + 1, y))  # lower cell
            stack.append((x - 1, y))  # upper cell
            stack.append((x, y + 1))  # right cell
            stack.append((x, y - 1))  # left cell


def main():
    sol = Solution()
    print(sol.floodFill([[0, 1, 1, 1, 0], [0, 0, 0, 1, 1], [
        0, 1, 1, 1, 0], [0, 1, 1, 0, 0], [0, 0, 0, 0, 0]], 1, 3, 2))
    print(sol.floodFill([[0, 0, 0, 0, 0], [0, 0, 0, 0, 0], [
        0, 0, 1, 1, 0], [0, 0, 1, 0, 0], [0, 0, 1, 0, 0]], 3, 2, 5))


main()

Time Complexity

Time complexity the above algorithm will be O(M * N), where ‘M’ is the number of rows and ‘N’ is the number of columns of the input matrix. This is due to the fact that, in the worst case, we might have to fill the whole matrix.

Space Complexity

DFS recursion stack can go O(M * N) deep when we have to fill the whole matrix. Hence, the space complexity will be O(M * N) , where ‘M’ is the number of rows and ‘N’ is the number of columns of the input matrix.

Number of Closed Islands

Similar | 1254. Number of Closed Islands Design Gurus Leetcode 中 ‘0’ and ‘1’的含义反过来了，所以只要改一下这个就过了

Problem Statement

You are given a 2D matrix containing only 1s (land) and 0s (water).

An island is a connected set of 1s (land) and is surrounded by either an edge or 0s (water). Each cell is considered connected to other cells horizontally or vertically (not diagonally).

A closed island is an island that is totally surrounded by 0s (i.e., water). This means all horizontally and vertically connected cells of a closed island are water. This also means that, by definition, a closed island can’t touch an edge (as then the edge cells are not connected to any water cell).

Write a function to find the number of closed islands in the given matrix.

Example 1

Input: matrix =

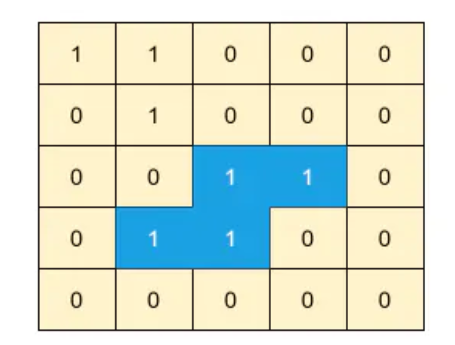
Output: 1 Explanation: The given matrix has two islands, but only the highlighted island is a closed island. The other island is touching the boundary that’s why is is not considered a closed island.

Example 2

Input: matrix =

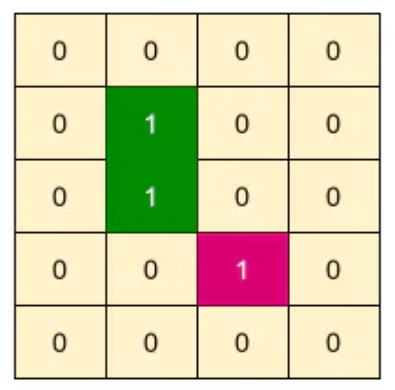
Output: 2

Explanation: The given matrix has two islands and both of them are closed islands.

Constraints:

  • 1 <= grid.length, grid[0].length <= 100
  • 0 <= grid[i][j] <=1

Solution

The question follows the Island pattern and is quite similar to Number of Islands problem.

We will traverse the matrix linearly to find islands. We can use the Depth First Search (DFS) or Breadth First Search (BFS) to traverse an island i.e., to find all of its connected land cells.

How do we decide if an island is a closed island?

To find that out, while traversing an island we need to ensure two things:

  1. The island does not touch an edge.
  2. Outside boundary of the island are water cells.

For the first condition, whenever we go outside the boundary of the matrix during DFS or BFS, it means that one of the cells of the island is touching an edge; so, the island is not closed. Following code will cover this condition:

1
2
if (x < 0 || x >= matrix.length || y < 0 || y >= matrix[0].length)
     return false; // returning false since the island is touching an edge

For the second condition, we need to ensure that all the boundary cells of the island are water. Following code will take care of that:

1
2
if (matrix[x][y] == 0 || visited[x][y])
     return true; // returning true as the island is surrounded by water

Here is the visual representation of the algorithm:

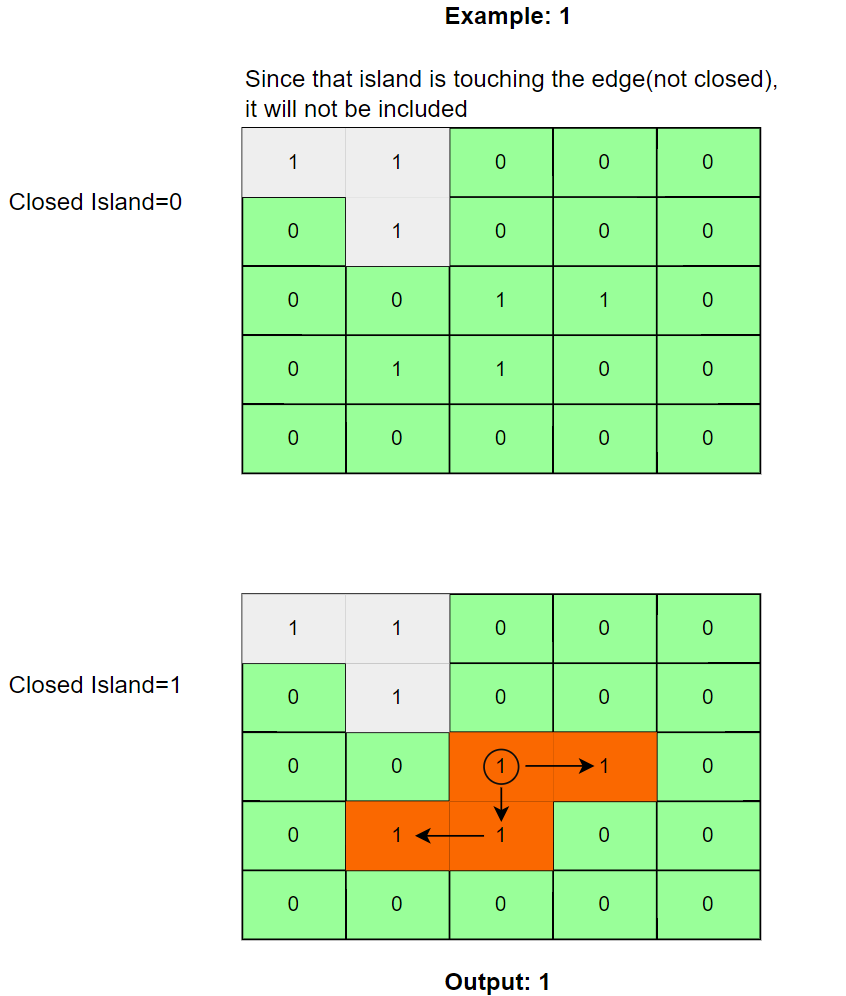
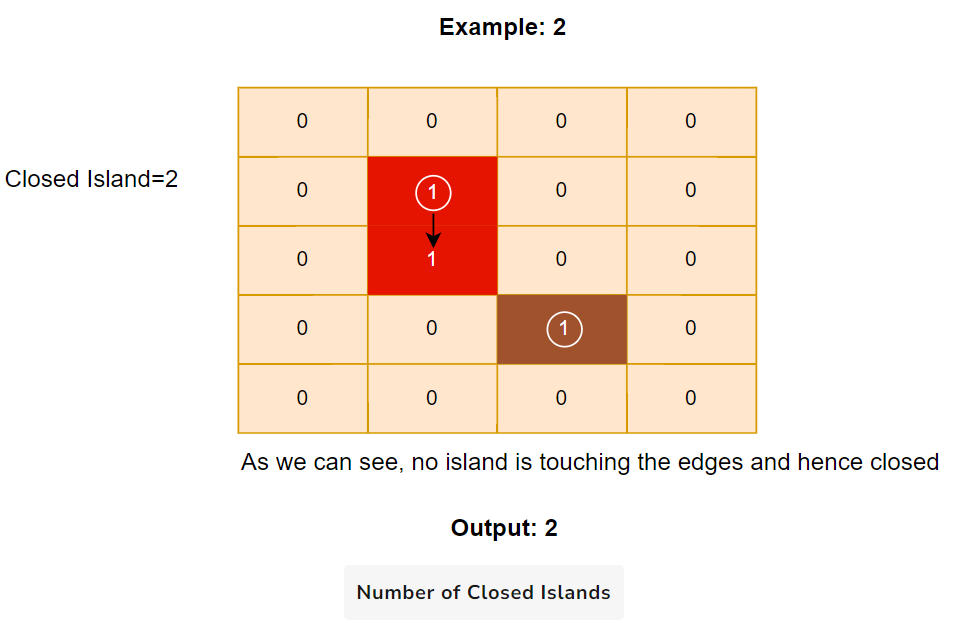
Code (DFS)

Here is what our DFS algorithm will look like. We will use a separate array to mark nodes visited.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
# 官方使用的是DFS的递归，但是我比较习惯使用while
class Solution:
    def countClosedIslands(self, matrix):
        rows = len(matrix)
        cols = len(matrix[0])
        visited = [[False for i in range(cols)] for j in range(rows)]
        countClosedIslands = 0

        for i in range(rows):
            for j in range(cols):
                # only if the cell is a land and not visited
                if (matrix[i][j] == 1 and not visited[i][j]):
                    if self.is_closed_is_land_DFS(matrix, visited, i, j):
                        countClosedIslands += 1

        return countClosedIslands


    def is_closed_is_land_DFS(self, matrix,  visited, x,  y):
        if (x < 0 or x >= len(matrix) or y < 0 or y >= len(matrix[0])):
            return False  # returning false since the island is touching an edge
        if (matrix[x][y] == 0 or visited[x][y]):
            return True  # returning true as the island is surrounded by water

        visited[x][y] = True  # mark the cell visited

        isClosed = True
        # recursively visit all neighboring cells (horizontally & vertically)
        isClosed &= self.is_closed_is_land_DFS(matrix, visited, x + 1, y)  # lower cell
        isClosed &= self.is_closed_is_land_DFS(matrix, visited, x - 1, y)  # upper cell
        isClosed &= self.is_closed_is_land_DFS(matrix, visited, x, y + 1)  # right cell
        isClosed &= self.is_closed_is_land_DFS(matrix, visited, x, y - 1)  # left cell

        return isClosed


def main():
  sol = Solution()
  print(sol.countClosedIslands([[1, 1, 0, 0, 0], [0, 1, 0, 0, 0], [
        0, 0, 1, 1, 0], [0, 1, 1, 0, 0], [0, 0, 0, 0, 0]]))

  print(sol.countClosedIslands([[0, 0, 0, 0], [0, 1, 0, 0], [
        0, 1, 0, 0], [0, 0, 1, 0], [0, 0, 0, 0]]))


main()

# 自己实现的DFS while，可以过leetcode
from collections import deque


class Solution:
    def countClosedIslands(self, matrix):
        rows = len(matrix)
        cols = len(matrix[0])
        visited = [[False for i in range(cols)] for j in range(rows)]
        countClosedIslands = 0

        for i in range(rows):
            for j in range(cols):
                # only if the cell is a land and not visited
                if (matrix[i][j] == 1 and not visited[i][j]):
                    if self.is_closed_is_land_DFS(matrix, visited, i, j):
                        countClosedIslands += 1

        return countClosedIslands

    def is_closed_is_land_DFS(self, matrix, visited, x, y):
        is_closed = True
        stack = deque([(x, y)])
        while stack:
            x, y = stack.pop()
            if x < 0 or x >= len(matrix) or y < 0 or y >= len(matrix[0]):
                continue  # returning false since the island is touching an edge
            if matrix[x][y] == 1 and (x == 0 or x == len(matrix) - 1 or y == 0 or y == len(matrix[0]) - 1):
                is_closed = False
            if matrix[x][y] == 0 or visited[x][y]:
                continue  # returning true as the island is surrounded by water

            visited[x][y] = True  # mark the cell visited
            # recursively visit all neighboring cells (horizontally & vertically)
            stack.append((x + 1, y))  # lower cell
            stack.append((x - 1, y))  # upper cell
            stack.append((x, y + 1))  # right cell
            stack.append((x, y - 1))  # left cell

        return is_closed


def main():
    sol = Solution()
    print(sol.countClosedIslands([[1, 1, 0, 0, 0], [0, 1, 0, 0, 0], [
        0, 0, 1, 1, 0], [0, 1, 1, 0, 0], [0, 0, 0, 0, 0]]))

    print(sol.countClosedIslands([[0, 0, 0, 0], [0, 1, 0, 0], [
        0, 1, 0, 0], [0, 0, 1, 0], [0, 0, 0, 0]]))


main()

Time Complexity

Time complexity of the above algorithm will be O(M * N), where ‘M’ is the number of rows and ‘N’ is the number of columns of the input matrix. This is due to the fact that we have to traverse the whole matrix to find islands.

Space Complexity

DFS recursion stack can go MN deep when the whole matrix is filled with ‘1’s. Hence, the space complexity will be **O(M \ N)**, where ‘M’ is the number of rows and ‘N’ is the number of columns of the input matrix.

Problem Challenge 1

463. Island Perimeter Design Gurus

Problem Statement

You are given a 2D matrix containing only 1s (land) and 0s (water).

An island is a connected set of 1s (land) and is surrounded by either an edge or 0s (water). Each cell is considered connected to other cells horizontally or vertically (not diagonally).

There are no lakes on the island, so the water inside the island is not connected to the water around it. A cell is a square with a side length of 1..

The given matrix has only one island, write a function to find the perimeter of that island.

Example 1

Input: matrix =

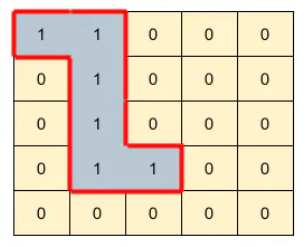
Output: 14

Explanation: The boundary of the island constitutes 14 sides.

Example 2

Input: matrix =

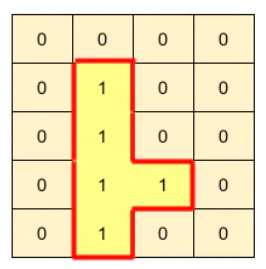
Output: 12

Explanation: The boundary of the island constitute 12 sides.

Solution

The question follows the Island pattern and is quite similar to Number of Islands problem.

We will traverse the matrix linearly to find the island. We can use the Depth First Search (DFS) or Breadth First Search (BFS) to traverse the island i.e., to find all of its connected land cells.

How do we calculate the boundary if the island?

Each cell has four sides. Each side of an island cell can be shared with another cell; we can include the side in the island perimeter only if the other cell is a water.

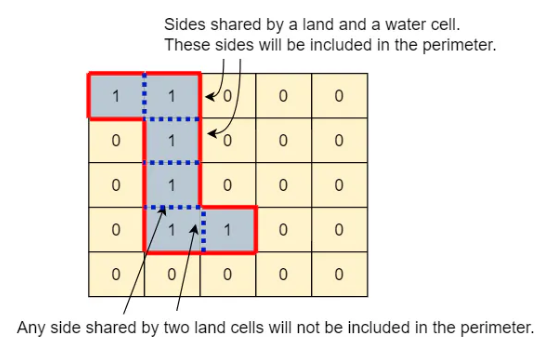
If a cell side is on boundary, we should include that side in the perimeter.

Following piece of code will cover these two conditions:

1
2
3
4
if (x < 0 || x >= matrix.length || y < 0 || y >= matrix[0].length)
   return 1; // returning 1, since this a boundary cell initiated this DFS call
 if (matrix[x][y] == 0)
   return 1; // returning 1, because of the shared side b/w a water and a land cell

Code (DFS)

Here is what our DFS algorithm will look like. We will use a separate matrix to mark nodes visited.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
# 官方使用的是DFS的递归，但是我比较习惯使用while
class Solution:
    def findIslandPerimeter(self, matrix):
        rows = len(matrix)
        cols = len(matrix[0])
        visited = [[False for i in range(cols)] for j in range(rows)]

        for i in range(rows):
            for j in range(cols):
                # only if the cell is a land and not visited
                if matrix[i][j] == 1 and not visited[i][j]:
                    return self.is_land_perimeter_DFS(matrix, visited, i, j)

        return 0

    def is_land_perimeter_DFS(self, matrix, visited, x, y):
        if x < 0 or x >= len(matrix) or y < 0 or y >= len(matrix[0]):
            return 1  # returning 1, since this a boundary cell initiated this DFS call

        if matrix[x][y] == 0:
            return 1  # returning 1, because of the shared side b/w a water and a land cell

        if visited[x][y]:  # 到这一步的时候，matrix[x][y]已经是1了
            return 0  # we have already taken care of this cell

        visited[x][y] = True  # mark the cell visited

        edgeCount = 0
        # recursively visit all neighboring cells (horizontally & vertically)
        edgeCount += self.is_land_perimeter_DFS(matrix, visited, x + 1, y)  # lower cell
        edgeCount += self.is_land_perimeter_DFS(matrix, visited, x - 1, y)  # upper cell
        edgeCount += self.is_land_perimeter_DFS(matrix, visited, x, y + 1)  # right cell
        edgeCount += self.is_land_perimeter_DFS(matrix, visited, x, y - 1)  # left cell

        return edgeCount


def main():
    sol = Solution()
    print(sol.findIslandPerimeter([[1, 1, 0, 0, 0],
                                   [0, 1, 0, 0, 0],
                                   [0, 1, 0, 0, 0],
                                   [0, 1, 1, 0, 0],
                                   [0, 0, 0, 0, 0]]))

    print(sol.findIslandPerimeter([[0, 0, 0, 0],
                                   [0, 1, 0, 0],
                                   [0, 1, 0, 0],
                                   [0, 1, 1, 0],
                                   [0, 1, 0, 0]]))


main()


# 自己实现的DFS while，可以过leetcode
from collections import deque


class Solution:
    def findIslandPerimeter(self, matrix):
        rows = len(matrix)
        cols = len(matrix[0])
        visited = [[False for i in range(cols)] for j in range(rows)]

        for i in range(rows):
            for j in range(cols):
                # only if the cell is a land and not visited
                if matrix[i][j] == 1 and not visited[i][j]:
                    return self.is_land_perimeter_DFS(matrix, visited, i, j)

        return 0

    def is_land_perimeter_DFS(self, matrix, visited, x, y):
        stack = deque([(x, y)])
        edge_count = 0
        while stack:
            x, y = stack.pop()
            if x < 0 or x >= len(matrix) or y < 0 or y >= len(matrix[0]):
                edge_count += 1  # returning 1, since this a boundary cell initiated this DFS call
                continue

            if matrix[x][y] == 0:
                edge_count += 1  # returning 1, because of the shared side b/w a water and a land cell
                continue

            if visited[x][y]:  # 到这一步的时候，matrix[x][y]已经是1了
                continue  # we have already taken care of this cell

            visited[x][y] = True  # mark the cell visited

            # recursively visit all neighboring cells (horizontally & vertically)
            stack.append((x + 1, y))  # lower cell
            stack.append((x - 1, y))  # upper cell
            stack.append((x, y + 1))  # right cell
            stack.append((x, y - 1))  # left cell

        return edge_count


def main():
    sol = Solution()
    print(sol.findIslandPerimeter([[1, 1, 0, 0, 0],
                                   [0, 1, 0, 0, 0],
                                   [0, 1, 0, 0, 0],
                                   [0, 1, 1, 0, 0],
                                   [0, 0, 0, 0, 0]]))

    print(sol.findIslandPerimeter([[0, 0, 0, 0],
                                   [0, 1, 0, 0],
                                   [0, 1, 0, 0],
                                   [0, 1, 1, 0],
                                   [0, 1, 0, 0]]))


main()

Time Complexity

Time complexity of the above algorithm will be O(M * N), where ‘M’ is the number of rows and ‘N’ is the number of columns of the input matrix. This is due to the fact that we have to traverse the whole matrix to find the island.

Space Complexity

DFS recursion stack can go O(M * N) deep when the whole matrix is filled with ‘1’s. Hence, the space complexity will be O(M * N), where ‘M’ is the number of rows and ‘N’ is the number of columns of the input matrix.

Problem Challenge 2

Leetcode 会员 Design Gurus

Problem Statement

You are given a 2D matrix containing only 1s (land) and 0s (water).

An island is a connected set of 1s (land) and is surrounded by either an edge or 0s (water). Each cell is considered connected to other cells horizontally or vertically (not diagonally).

Two islands are considered the same if and only if they can be translated (not rotated or reflected) to equal each other.

Write a function to find the number of distinct islands in the given matrix.

Example 1

Input: matrix =

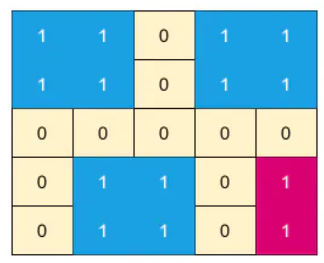
Output: 2

Explanation: There are four islands in the given matrix, but three of them are the same; hence, there are only two distinct islands.

Example 2

Input: matrix =

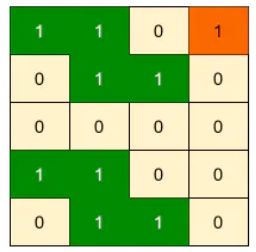
Output: 2

Explanation: There are three islands in the given matrix, but two of them are the same; hence, there are only two distinct islands.

Solution

The question follows the Island pattern and is quite similar to Number of Islands problem.

We will traverse the matrix linearly to find islands. We can use the Depth First Search (DFS) or Breadth First Search (BFS) to traverse an island i.e., to find all of its connected land cells.

How do we decide if two islands are same?

If two islands are same, their traversal path should be same too. This means, if we perform a DFS or BFS on two equal islands starting from their top-left cell, the traversal pattern should be exactly same for both the islands. For example, here is the DFS traversal of the example-2 mentioned above:

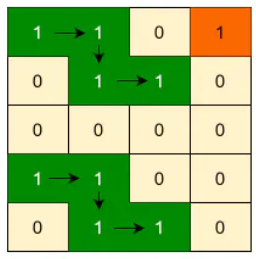
We can clearly see that the two equal islands have same traversal pattern.

We can utilize this fact to develop an algorithm.

While traversing an island, we can construct a string that maps the traversal path of the island. For example, here is the DFS traversal of the two same islands mentioned in Example-2 ( ‘R’ for right move, ‘D’ for down move, ‘O’ for origin denoting the start): ORDR

We can start inserting these traversal strings of each island in a HashSet. This will ensure that we will not have any duplicate traversal string in the HashSet, thus giving us distinct islands. When we finish traversing the matrix, the HashSet will contain the distinct traversal path of all islands. Hence, the total number of elements in the HashSet will be equal to distinct number of islands.

Code

Here is the code for this algorithm:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
# 官方使用的是DFS的递归，但是我比较习惯使用while
class Solution:
    def findDistinctIslandsDFS(self, matrix):
        rows = len(matrix)
        cols = len(matrix[0])
        visited = [[False for i in range(cols)] for j in range(rows)]
        islandsSet = set()

        for i in range(rows):
            for j in range(cols):
                # only if the cell is a land and not visited
                if (matrix[i][j] == 1 and not visited[i][j]):
                    traversal = self.traverse_is_land_DFS(matrix, visited, i, j, "O");  # origin
                    islandsSet.add(traversal)

        return len(islandsSet)

    def traverse_is_land_DFS(self, matrix, visited, x, y, direction):
        if x < 0 or x >= len(matrix) or y < 0 or y >= len(matrix[0]):
            return ""  # return if it is not a valid cell

        if matrix[x][y] == 0 or visited[x][y]:
            return ""  # return if it is a water cell or is visited

        visited[x][y] = True  # mark the cell visited

        islandTraversal = direction
        # recursively visit all neighboring cells (horizontally & vertically)
        islandTraversal += self.traverse_is_land_DFS(matrix, visited, x + 1, y, "D")  # down
        islandTraversal += self.traverse_is_land_DFS(matrix, visited, x - 1, y, "U")  # up
        islandTraversal += self.traverse_is_land_DFS(matrix, visited, x, y + 1, "R")  # right
        islandTraversal += self.traverse_is_land_DFS(matrix, visited, x, y - 1, "L")  # left

        islandTraversal += "B"  # back

        return islandTraversal


def main():
    sol = Solution()
    print(sol.findDistinctIslandsDFS([[1, 1, 0, 1, 1],
                                      [1, 1, 0, 1, 1],
                                      [0, 0, 0, 0, 0],
                                      [0, 1, 1, 0, 1],
                                      [0, 1, 1, 0, 1]]))

    print(sol.findDistinctIslandsDFS([[1, 1, 0, 1],
                                      [0, 1, 1, 0],
                                      [0, 0, 0, 0],
                                      [1, 1, 0, 0],
                                      [0, 1, 1, 0]]))


main()


# 自己实现的DFS while，可以过leetcode
from collections import deque


class Solution:
    def findDistinctIslandsDFS(self, matrix):
        rows = len(matrix)
        cols = len(matrix[0])
        visited = [[False for i in range(cols)] for j in range(rows)]
        islandsSet = set()

        for i in range(rows):
            for j in range(cols):
                # only if the cell is a land and not visited
                if (matrix[i][j] == 1 and not visited[i][j]):
                    traversal = self.traverse_is_land_DFS(matrix, visited, i, j, "O");  # origin
                    islandsSet.add(traversal)

        return len(islandsSet)

    def traverse_is_land_DFS(self, matrix, visited, x, y, direction):
        stack = deque([(x, y, direction)])
        islandTraversal = ''
        while stack:
            x, y, direction = stack.pop()
            if x < 0 or x >= len(matrix) or y < 0 or y >= len(matrix[0]):
                continue  # return if it is not a valid cell

            if matrix[x][y] == 0 or visited[x][y]:
                continue  # return if it is a water cell or is visited

            visited[x][y] = True  # mark the cell visited
            islandTraversal += direction
            # recursively visit all neighboring cells (horizontally & vertically)
            stack.append((x + 1, y, "D"))  # down
            stack.append((x - 1, y, "U"))  # up
            stack.append((x, y + 1, "R"))  # right
            stack.append((x, y - 1, "L"))  # left


        return islandTraversal


def main():
    sol = Solution()
    print(sol.findDistinctIslandsDFS([[1, 1, 0, 1, 1],
                                      [1, 1, 0, 1, 1],
                                      [0, 0, 0, 0, 0],
                                      [0, 1, 1, 0, 1],
                                      [0, 1, 1, 0, 1]]))

    print(sol.findDistinctIslandsDFS([[1, 1, 0, 1],
                                      [0, 1, 1, 0],
                                      [0, 0, 0, 0],
                                      [1, 1, 0, 0],
                                      [0, 1, 1, 0]]))


main()

Time Complexity

Time complexity of the above algorithm will be O(M * N), where ‘M’ is the number of rows and ‘N’ is the number of columns of the input matrix. This is due to the fact that we have to traverse the whole matrix to find islands.

Space Complexity

DFS recursion stack can go MN deep when the whole matrix is filled with ‘1’s. Hence, the space complexity will be **O(M \ N)**, where ‘M’ is the number of rows and ‘N’ is the number of columns of the input matrix.

Problem Challenge 3

1559. Detect Cycles in 2D Grid Design Gurus

Problem Statement

You are given a 2D matrix containing different characters, you need to find if there exists any cycle consisting of the same character in the matrix.

A cycle is a path in the matrix that starts and ends at the same cell and has four or more cells. From a given cell, you can move to one of the cells adjacent to it - in one of the four directions (up, down, left, or right), if it has the same character value of the current cell.

Write a function to find if the matrix has a cycle.

Example 1

Input: matrix =

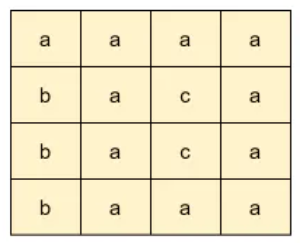
Output: true

Explanation: The given matrix has a cycle as shown below:

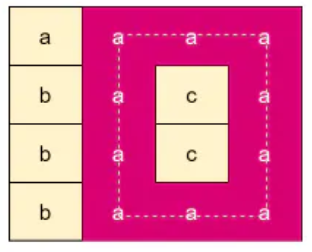
Example 2

Input: matrix =

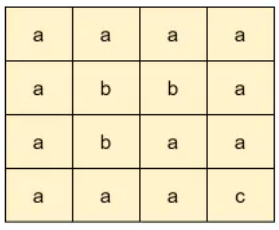
Output: true

Explanation: The given matrix has one cycle as shown below:

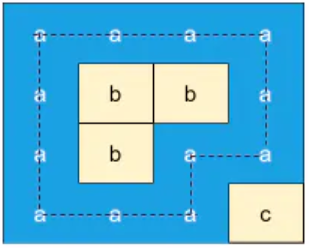
Example 3

Input: matrix =

Output: false

Explanation: The given matrix has no cycle.

Constraints:

  • m == matrix.length
  • n == matrix[i].length
  • 1 <= m, n <= 500
  • matrix[i][j] is ‘0’ or ‘1’.

Solution

The question follows the Island pattern and is quite similar to Number of Islands problem.

We will traverse the matrix linearly to find any cycle. Each cycle is like an island having cells containing same values. Hence, we can use the Depth First Search (DFS) or Breadth First Search (BFS) to traverse a cycle i.e., to find all of its connected cells with the same value.

Our approach for traversing the matrix will be similar to the one we used when searching for islands. We will keep another matrix to remember the cells that we have visited. From any given cell, we can perform DFS to traverse all the neighboring cells having the same character value.

Whenever we reach a cell that have already been visited, we can conclude that we have found a cycle. This also means that we need to be careful to not start traversing the parent cell and wrongly finding a cycle. That is, while traversing, when initiating DFS recursive calls to all the neighboring cell, we should not start a DFS call to the pervious cell, Here is the visual representation of the algorithm:

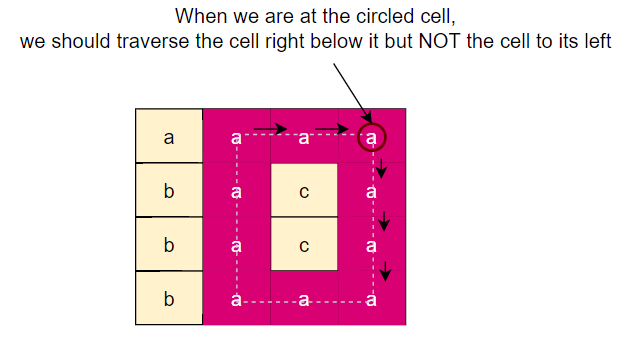
Code

Here is the code for this algorithm:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
# 官方使用的是DFS的递归，但是我比较习惯使用while
class Solution:
    def hasCycle(self, matrix):
        rows = len(matrix)
        cols = len(matrix[0])
        visited = [[False for i in range(cols)] for j in range(rows)]

        for i in range(rows):
            for j in range(cols):
                if (not visited[i][j]):  # only if the cell is not visited
                    if (self.contains_cycle_DFS(matrix, visited, matrix[i][j], i, j, -1, -1)):
                        return True
        return False


    def contains_cycle_DFS(self, matrix, visited, startChar, x,  y, prevX, prevY):
        if (x < 0 or x >= len(matrix) or y < 0 or y >= len(matrix[0])):
            return False  # not a valid cell

        if (matrix[x][y] != startChar):
            return False  # different character which means a different island

        if (visited[x][y]):
            return True  # found a cycle, as we are visiting an already visited valid cell

        visited[x][y] = True  # mark the cell visited

        # recursively visit all neighboring cells (horizontally & vertically)
        if (x + 1 != prevX and self.contains_cycle_DFS(matrix, visited, startChar, x + 1, y, x, y)): # down
            return True
        if (x - 1 != prevX and self.contains_cycle_DFS(matrix, visited, startChar, x - 1, y, x, y)): # up
            return True
        if (y + 1 != prevY and self.contains_cycle_DFS(matrix, visited, startChar, x, y + 1, x, y)): # right
            return True
        if (y - 1 != prevY and self.contains_cycle_DFS(matrix, visited, startChar, x, y - 1, x, y)): # left
            return True

        return False


def main():
    sol = Solution()
    print(sol.hasCycle([['a', 'a', 'a', 'a'],
                    ['b', 'a', 'c', 'a'],
                    ['b', 'a', 'c', 'a'],
                    ['b', 'a', 'a', 'a']]))

    print(sol.hasCycle([['a', 'a', 'a', 'a'],
                    ['a', 'b', 'b', 'a'],
                    ['a', 'b', 'a', 'a'],
                    ['a', 'a', 'a', 'c']]))

    print(sol.hasCycle([['a', 'b', 'e', 'b'],
                    ['b', 'b', 'b', 'b'],
                    ['b', 'c', 'c', 'd'],
                    ['c', 'c', 'd', 'd']]))


main()

# 自己实现的DFS while，可以过leetcode
from collections import deque


class Solution:
    def hasCycle(self, matrix):
        rows = len(matrix)
        cols = len(matrix[0])
        visited = [[False for i in range(cols)] for j in range(rows)]

        for i in range(rows):
            for j in range(cols):
                if not visited[i][j]:  # only if the cell is not visited
                    if self.contains_cycle_DFS(matrix, visited, matrix[i][j], i, j, -1, -1):
                        return True
        return False

    def contains_cycle_DFS(self, matrix, visited, startChar, x, y, prevX, prevY):
        stack = deque([(x, y, prevX, prevY)])
        while stack:
            x, y, prevX, prevY = stack.pop()
            if x < 0 or x >= len(matrix) or y < 0 or y >= len(matrix[0]):
                continue  # not a valid cell

            if matrix[x][y] != startChar:
                continue  # different character which means a different island

            if visited[x][y]:
                return True  # found a cycle, as we are visiting an already visited valid cell

            visited[x][y] = True  # mark the cell visited

            # recursively visit all neighboring cells (horizontally & vertically)
            if x + 1 != prevX:
                stack.append((x + 1, y, x, y))  # down
            if x - 1 != prevX:
                stack.append((x - 1, y, x, y))  # up
            if y + 1 != prevY:
                stack.append((x, y + 1, x, y))  # right
            if y - 1 != prevY:
                stack.append((x, y - 1, x, y))  # left

        return False


def main():
    sol = Solution()
    print(sol.hasCycle([['a', 'a', 'a', 'a'],
                        ['b', 'a', 'c', 'a'],
                        ['b', 'a', 'c', 'a'],
                        ['b', 'a', 'a', 'a']]))

    print(sol.hasCycle([['a', 'a', 'a', 'a'],
                        ['a', 'b', 'b', 'a'],
                        ['a', 'b', 'a', 'a'],
                        ['a', 'a', 'a', 'c']]))

    print(sol.hasCycle([['a', 'b', 'e', 'b'],
                        ['b', 'b', 'b', 'b'],
                        ['b', 'c', 'c', 'd'],
                        ['c', 'c', 'd', 'd']]))


main()

Time Complexity

Time complexity of the above algorithm will be O(M * N), where ‘M’ is the number of rows and ‘N’ is the number of columns of the input matrix. This is due to the fact that we have to traverse the whole matrix to find cycles.

Space Complexity

DFS recursion stack can go MN deep when the whole matrix is filled with the same character. Hence, the space complexity will be **O(M \ N)**, where ‘M’ is the number of rows and ‘N’ is the number of columns of the input matrix.

Author：Hasuer

Link：https://hasuer.github.io/13-pattern-island-matrix-traversal/index.html

Publish date：May 13th 2024, 9:43:32 am

Update date：May 28th 2024, 11:28:55 am

License：本文采用知识共享署名-非商业性使用 4.0 国际许可协议进行许可

CATALOG
  1. 1. Introduction to Island Pattern
  2. 2. Number of Islands
    1. 2.1. Problem Statement
    2. 2.2. Solution
    3. 2.3. Code (DFS)
    4. 2.4. Code (DFS) (DFS with visited matrix)
    5. 2.5. Code (BFS)
    6. 2.6. Code (BFS with visited matrix)
  3. 3. Biggest Island
    1. 3.1. Problem Statement
    2. 3.2. Solution
    3. 3.3. Code (DFS)
    4. 3.4. Complexity Analysis
  4. 4. Flood Fill
    1. 4.1. Problem Statement
    2. 4.2. Solution
    3. 4.3. Code (DFS)
    4. 4.4. Time Complexity
    5. 4.5. Space Complexity
  5. 5. Number of Closed Islands
    1. 5.1. Problem Statement
    2. 5.2. Solution
    3. 5.3. Code (DFS)
    4. 5.4. Time Complexity
    5. 5.5. Space Complexity
  6. 6. Problem Challenge 1
    1. 6.1. Problem Statement
    2. 6.2. Solution
    3. 6.3. Code (DFS)
    4. 6.4. Time Complexity
    5. 6.5. Space Complexity
  7. 7. Problem Challenge 2
    1. 7.1. Problem Statement
    2. 7.2. Solution
    3. 7.3. Code
    4. 7.4. Time Complexity
    5. 7.5. Space Complexity
  8. 8. Problem Challenge 3
    1. 8.1. Problem Statement
    2. 8.2. Solution
    3. 8.3. Code
    4. 8.4. Time Complexity
    5. 8.5. Space Complexity
Total : 41
2024
2022
2021
Interview
技术笔记 Grokking-Interview-Pattern