Hasuer's Studio.

15. Pattern Subsets

Grokking Interview Pattern Interview
Word count: 6.4kReading time: 38 min
2024/05/15

Introduction to Subsets Pattern

A huge number of coding interview problems involve dealing with Permutations and Combinations of a given set of elements. This pattern describes an efficient Breadth First Search (BFS) approach to handle all these problems.

Let’s jump onto our first problem to develop an understanding of this pattern.

*Subsets (easy)

78. Subsets Design Gurus Educative.io

Problem Statement

Given a set with distinct elements, find all of its distinct subsets.

Example 1:

1
2
Input: [1, 3]
Output: [], [1], [3], [1,3]

Example 2:

1
2
Input: [1, 5, 3]
Output: [], [1], [5], [3], [1,5], [1,3], [5,3], [1,5,3]

Constraints:

  • 1 <= nums.length <= 10
  • -10 <= nums[i] <= 10
  • All the numbers of nums are unique.

Solution

To generate all subsets of the given set, we can use the Breadth First Search (BFS) approach. We can start with an empty set, iterate through all numbers one-by-one, and add them to existing sets to create new subsets.

Let’s take the example-2 mentioned above to go through each step of our algorithm:

Given set: [1, 5, 3]

  1. Start with an empty set: [[]]
  2. Add the first number (1) to all the existing subsets to create new subsets: [[], [1]];
  3. Add the second number (5) to all the existing subsets: [[], [1], [5], [1,5]];
  4. Add the third number (3) to all the existing subsets: [[], [1], [5], [1,5], [3], [1,3], [5,3], [1,5,3]].

Here is the visual representation of the above steps:

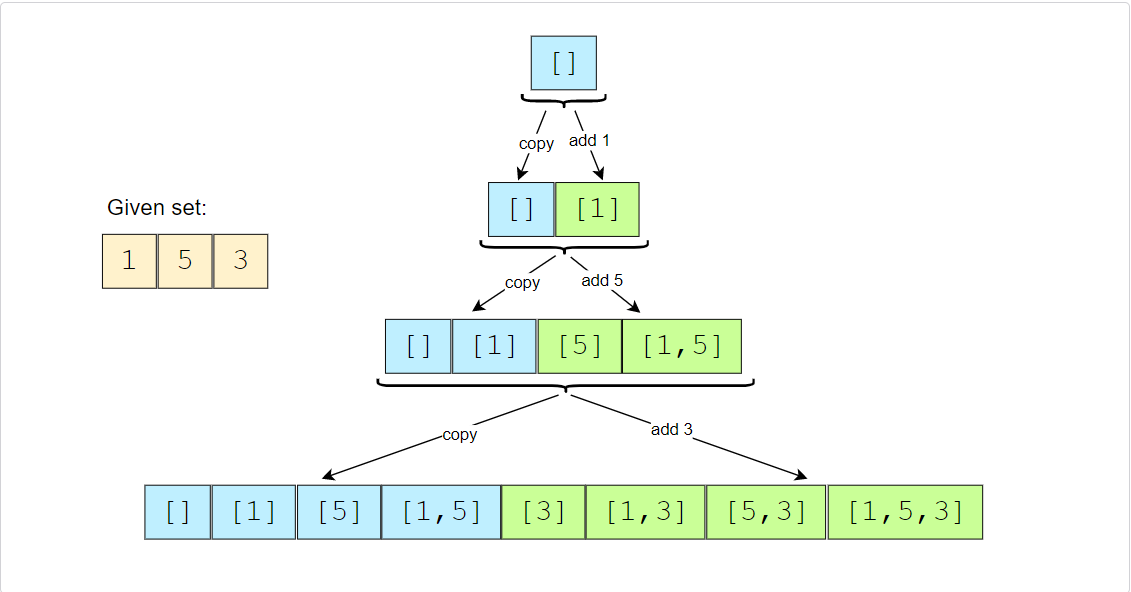
Since the input set has distinct elements, the above steps will ensure that we will not have any duplicate subsets.

Code

Here is what our algorithm will look like:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution:
    def findSubsets(self, nums):
        subsets = []
        # start by adding the empty subset
        subsets.append([])
        for currentNumber in nums:
            # we will take all existing subsets and insert the current number in them to create 
            # new subsets
            n = len(subsets)
            for i in range(n):
                # create a new subset from the existing subset and insert the current element to it
                set1 = list(subsets[i])
                set1.append(currentNumber)
                subsets.append(set1)

        return subsets


def main():
    sol = Solution()
    print("Here is the list of subsets: " + str(sol.findSubsets([1, 3])))
    print("Here is the list of subsets: " + str(sol.findSubsets([1, 5, 3])))


main()

Time complexity

Since, in each step, the number of subsets doubles as we add each element to all the existing subsets, the time complexity of the above algorithm is O(2^N), where ‘N’ is the total number of elements in the input set. This also means that, in the end, we will have a total of O(2^N) subsets.

Space complexity

All the additional space used by our algorithm is for the output list. Since we will have a total of O(2^N) subsets, the space complexity of our algorithm is also O(2^N).

Subsets With Duplicates (easy)

90. Subsets II Design Gurus Educative.io

Problem Statement

Given a set of numbers that might contain duplicates, find all of its distinct subsets.

Example 1:l9

1
2
Input: [1, 3, 3]
Output: [], [1], [3], [1,3], [3,3], [1,3,3]

Example 2:

1
2
Input: [1, 5, 3, 3]
Output: [], [1], [5], [3], [1,5], [1,3], [5,3], [1,5,3], [3,3], [1,3,3], [3,3,5], [1,5,3,3]

Constraints:

  • 1 <= nums.length <= 10
  • -10 <= nums[i] <= 10

Solution

This problem follows the Subsets pattern and we can follow a similar Breadth First Search (BFS) approach. The only additional thing we need to do is handle duplicates. Since the given set can have duplicate numbers, if we follow the same approach discussed in Subsets, we will end up with duplicate subsets, which is not acceptable. To handle this, we will do two extra things:

  1. Sort all numbers of the given set. This will ensure that all duplicate numbers are next to each other.
  2. Follow the same BFS approach but whenever we are about to process a duplicate (i.e., when the current and the previous numbers are same), instead of adding the current number (which is a duplicate) to all the existing subsets, only add it to the subsets which were created in the previous step.

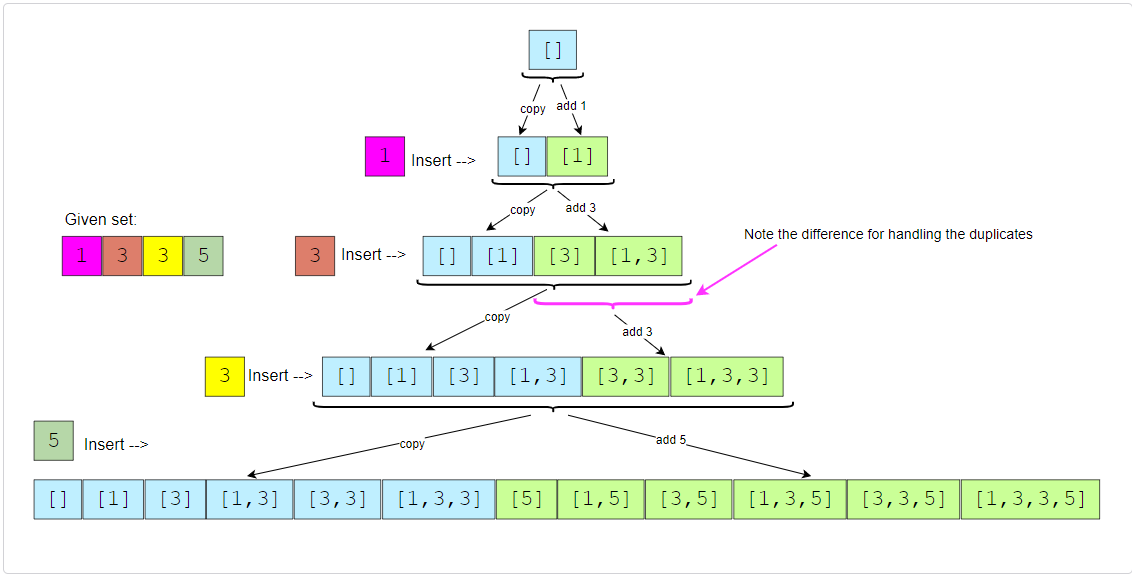
Let’s take Example-2 mentioned above to go through each step of our algorithm:

1
2
Given set: [1, 5, 3, 3]  
Sorted set: [1, 3, 3, 5]
  1. Start with an empty set: [[]]
  2. Add the first number (1) to all the existing subsets to create new subsets: [[], [1]];
  3. Add the second number (3) to all the existing subsets: [[], [1], [3], [1,3]].
  4. The next number (3) is a duplicate. If we add it to all existing subsets we will get:
1
2
3
    [[], [1], [3], [1,3], [3], [1,3], [3,3], [1,3,3]]
We got two duplicate subsets: [3], [1,3]  
Whereas we only needed the new subsets: [3,3], [1,3,3]

To handle this instead of adding (3) to all the existing subsets, we only add it to the new subsets which were created in the previous (3rd) step:

1
[[], [1], [3], [1,3], [3,3], [1,3,3]]
  1. Finally, add the forth number (5) to all the existing subsets: [[], [1], [3], [1,3], [3,3], [1,3,3], [5], [1,5], [3,5], [1,3,5], [3,3,5], [1,3,3,5]]

Here is the visual representation of the above steps:

Code

Here is what our algorithm will look like:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution:
    def findSubsets(self, nums):
        # sort the numbers to handle duplicates
        list.sort(nums)  # 或者nums.sort()
        subsets = []
        subsets.append([])
        start_index, end_index = 0, 1  # 表示上一步中加入到subsets中的元素的start和end+1
        for i in range(len(nums)):
            startIndex = 0  # 每次都要重置
            # if current and the previous elements are same, create new subsets only from the
            # subsets added in the previous step
            if i > 0 and nums[i] == nums[i - 1]:
                startIndex = endIndex
            endIndex = len(subsets)
            for j in range(startIndex, endIndex):
                # 这里的list很重要，这样才是重新复制了一个
                # create a new subset from the existing subset and add the current element to it
                set1 = list(subsets[j])
                set1.append(nums[i])
                subsets.append(set1)
        return subsets


def main():
    sol = Solution()
    print("Here is the list of subsets: " + str(sol.findSubsets([1, 3, 3])))
    print("Here is the list of subsets: " + str(sol.findSubsets([1, 5, 3, 3])))


main()

Time complexity

Since, in each step, the number of subsets could double (if not duplicate) as we add each element to all the existing subsets, the time complexity of the above algorithm is O(2^N), where ‘N’ is the total number of elements in the input set. This also means that, in the end, we will have a total of O(2^N) subsets at the most.

Space complexity

All the additional space used by our algorithm is for the output list. Since at most we will have a total of O(2^N) subsets, the space complexity of our algorithm is also O(2^N).

*Permutations (medium)

Top Interview 150 | 46. Permutations Design Gurus Educative.io

Problem Statement

Given a set of distinct numbers, find all of its permutations.

Permutation is defined as the re-arranging of the elements of the set. For example, {1, 2, 3} has the following six permutations:

  1. {1, 2, 3}
  2. {1, 3, 2}
  3. {2, 1, 3}
  4. {2, 3, 1}
  5. {3, 1, 2}
  6. {3, 2, 1}

If a set has ‘n’ distinct elements it will have n!n! permutations.

Example 1:

1
2
Input: [1,3,5]
Output: [1,3,5], [1,5,3], [3,1,5], [3,5,1], [5,1,3], [5,3,1]

Constraints:

  • 1 <= nums.length <= 6
  • -10 <= nums[i] <= 10
  • All the numbers of nums are unique.

Solution

This problem follows the Subsets pattern and we can follow a similar Breadth First Search (BFS) approach. However, unlike Subsets, every permutation must contain all the numbers.

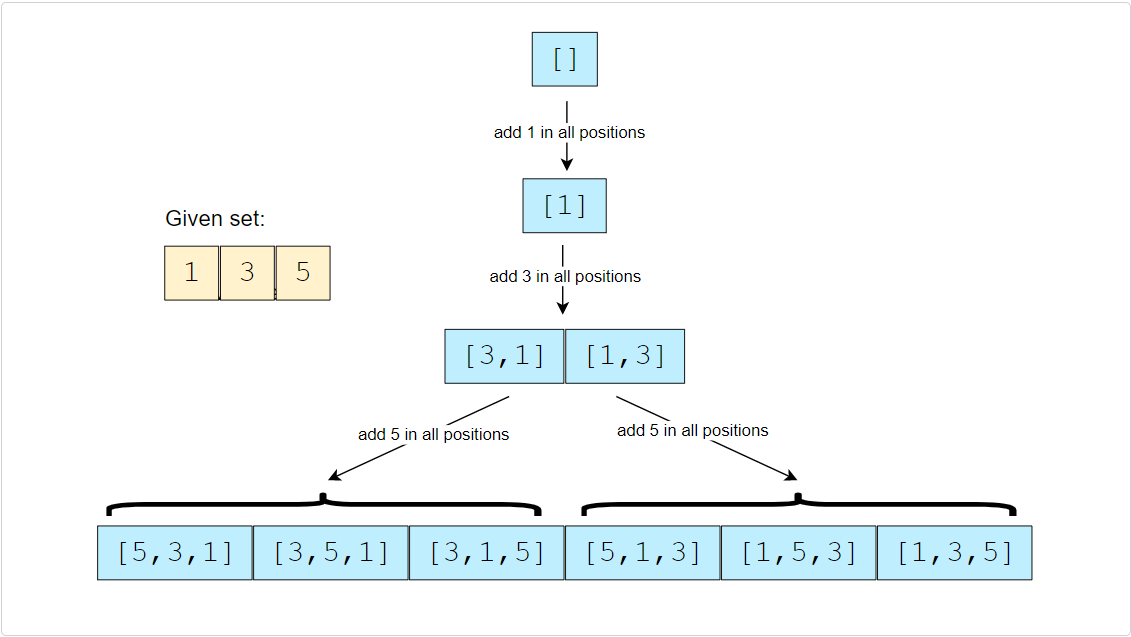
Let’s take the example-1 mentioned above to generate all the permutations. Following a BFS approach, we will consider one number at a time:

  1. If the given set is empty then we have only an empty permutation set: []
  2. Let’s add the first element (1), the permutations will be: [1]
  3. Let’s add the second element (3), the permutations will be: [3,1], [1,3]
  4. Let’s add the third element (5), the permutations will be: [5,3,1], [3,5,1], [3,1,5], [5,1,3], [1,5,3], [1,3,5]

Let’s analyze the permutations in the 3rd and 4th step. How can we generate permutations in the 4th step from the permutations of the 3rd step?

If we look closely, we will realize that when we add a new number (5), we take each permutation of the previous step and insert the new number in every position to generate the new permutations. For example, inserting ‘5’ in different positions of [3,1] will give us the following permutations:

  1. Inserting ‘5’ before ‘3’: [5,3,1]
  2. Inserting ‘5’ between ‘3’ and ‘1’: [3,5,1]
  3. Inserting ‘5’ after ‘1’: [3,1,5]

Here is the visual representation of this algorithm:

Code

Here is what our algorithm will look like:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
# 觉得的solution code有可以优化的地方，也过了leetcode
from collections import deque


class Solution:
    def findPermutations(self, nums):
        permutations = deque()
        permutations.append([])
        for currentNumber in nums:
            # we will take all existing permutations and add the current number to create
            # new permutations
            n = len(permutations)
            for _ in range(n):
                oldPermutation = permutations.popleft()
                # 这里的+1要记得写上，不然会有问题
                # create a new permutation by adding the current number at every position
                for j in range(len(oldPermutation) + 1):
                    newPermutation = list(oldPermutation)
                    newPermutation.insert(j, currentNumber)
                    permutations.append(newPermutation)

        return permutations


def main():
    sol = Solution()
    print("Here are all the permutations: " + str(sol.findPermutations([1, 3, 5])))


main()


# 官方版本
from collections import deque


class Solution:
    def findPermutations(self, nums):
        numsLength = len(nums)
        result = []
        permutations = deque()
        permutations.append([])
        for currentNumber in nums:
            # we will take all existing permutations and add the current number to create
            # new permutations
            n = len(permutations)
            for _ in range(n):
                oldPermutation = permutations.popleft()
                # 这里的+1要记得写上，不然会有问题
                # create a new permutation by adding the current number at every position
                for j in range(len(oldPermutation) + 1):
                    newPermutation = list(oldPermutation)
                    newPermutation.insert(j, currentNumber)
                    # 这里如果直接放到permutations里面，最后返回的时候，permutations里的就是答案
                    # 所以其实没有必要再用一个result,这样可以节约空间复杂度
                    if len(newPermutation) == numsLength:
                        result.append(newPermutation)
                    else:
                        permutations.append(newPermutation)

        return result


def main():
    sol = Solution()
    print("Here are all the permutations: " + str(sol.findPermutations([1, 3, 5])))


main()

Time complexity

We know that there are a total of N!N! permutations of a set with ‘N’ numbers. In the algorithm above, we are iterating through all of these permutations with the help of the two ‘for’ loops. In each iteration, we go through all the current permutations to insert a new number in them on line 17 (line 23 for C++ solution). To insert a number into a permutation of size ‘N’ will take O(N), which makes the overall time complexity of our algorithm O(N\N!)*.

Space complexity

All the additional space used by our algorithm is for the result list and the queue to store the intermediate permutations. If you see closely, at any time, we don’t have more than N!N! permutations between the result list and the queue. Therefore the overall space complexity to store N!N! permutations each containing NN elements will be O(N\N!)*.

Recursive Solution

Here is the recursive algorithm following a similar approach:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution:
    def generate_permutations(self, nums):
        result = []
        self.generate_permutations_recursive(nums, 0, [], result)
        return result

    def generate_permutations_recursive(self, nums, index, currentPermutation, result):
        if index == len(nums):
            result.append(currentPermutation)
        else:
            # create a new permutation by adding the current number at every position
            for i in range(len(currentPermutation) + 1):
                newPermutation = list(currentPermutation)
                newPermutation.insert(i, nums[index])
                self.generate_permutations_recursive(
                    nums, index + 1, newPermutation, result)


def main():
    sol = Solution()
    print("Here are all the permutations: " + str(sol.generate_permutations([1, 3, 5])))


main()

String Permutations by changing case (medium)

784. Letter Case Permutation Design Gurus Educative.io

Problem Statement

Given a string, find all of its permutations preserving the character sequence but changing case.

Example 1:

1
2
Input: "ad52"
Output: "ad52", "Ad52", "aD52", "AD52"

Example 2:

1
2
Input: "ab7c"
Output: "ab7c", "Ab7c", "aB7c", "AB7c", "ab7C", "Ab7C", "aB7C", "AB7C"

Constraints:

  • 1 <= str.length <= 12
  • str consists of lowercase English letters, uppercase English letters, and digits.

Solution

This problem follows the Subsets pattern and can be mapped to Permutations.

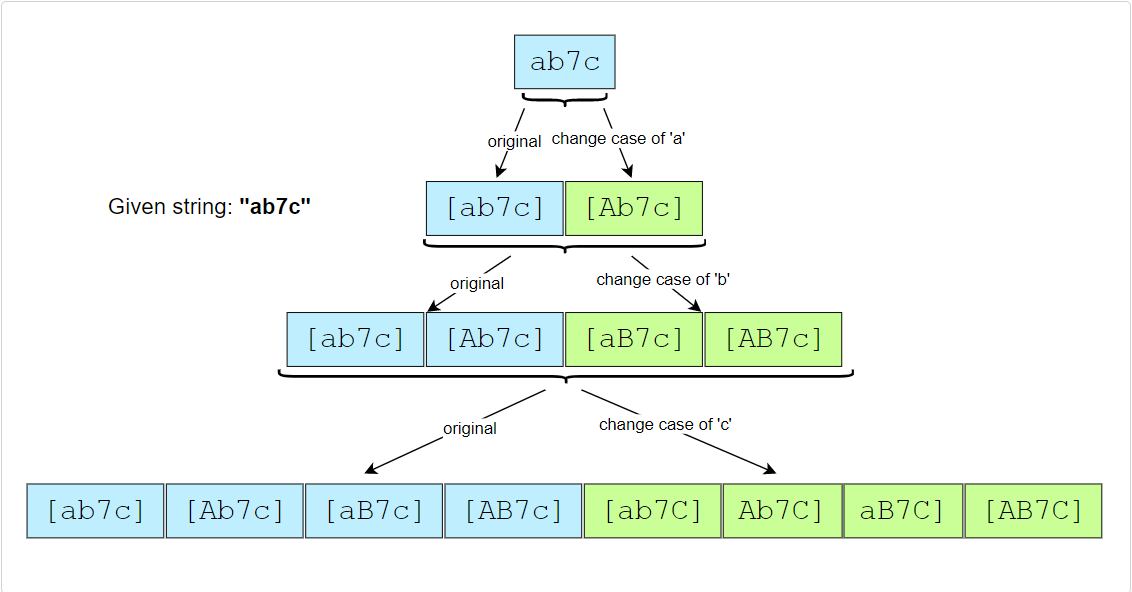
Let’s take Example-2 mentioned above to generate all the permutations. Following a BFS approach, we will consider one character at a time. Since we need to preserve the character sequence, we can start with the actual string and process each character (i.e., make it upper-case or lower-case) one by one:

  1. Starting with the actual string: "ab7c"
  2. Processing the first character (‘a’), we will get two permutations: "ab7c", "Ab7c"
  3. Processing the second character (‘b’), we will get four permutations: "ab7c", "Ab7c", "aB7c", "AB7c"
  4. Since the third character is a digit, we can skip it.
  5. Processing the fourth character (‘c’), we will get a total of eight permutations: "ab7c", "Ab7c", "aB7c", "AB7c", "ab7C", "Ab7C", "aB7C", "AB7C"

Let’s analyze the permutations in the 3rd and the 5th step. How can we generate the permutations in the 5th step from the permutations in the 3rd step?

If we look closely, we will realize that in the 5th step, when we processed the new character (‘c’), we took all the permutations of the previous step (3rd) and changed the case of the letter (‘c’) in them to create four new permutations.

Here is the visual representation of this algorithm:

Code

Here is what our algorithm will look like:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Solution:
    def findLetterCaseStringPermutations(self, str):
        permutations = [string]  # 下面两句等于这句
        # permutations = []
        # permutations.append(string)
        # process every character of the string one by one
        for i in range(len(str)):
            if str[i].isalpha():  # only process characters, skip digits
                # we will take all existing permutations and change the letter case appropriately
                n = len(permutations)
                for j in range(n):
                    chs = list(permutations[j])
                    # if the current char is in upper case, change it to lower case or vice versa
                    chs[i] = chs[i].swapcase()
                    permutations.append(''.join(chs))
                    # 原来打算这么写，但是python中不允许str[i] = char这样修改,TypeError: 'str' object does not support item assignment
                    # python没有字符的概念print(type('1')) => <class 'str'>
                    # new_string = permutations[j]
                    # new_string[i] = new_string[i].swapcase()
                    # permutations.append(new_string)
        return permutations


def main():
    sol = Solution()
    print("String permutations are: " +
          str(sol.findLetterCaseStringPermutations("ad52")))
    print("String permutations are: " +
          str(sol.findLetterCaseStringPermutations("ab7c")))


main()

Time complexity

Since we can have 2^N permutations at the most and while processing each permutation we convert it into a character array, the overall time complexity of the algorithm will be O(N\2^N)*.

Space complexity

All the additional space used by our algorithm is for the output list. Since we can have a total of O(2^N) permutations, the space complexity of our algorithm is O(N\2^N)*.

*Balanced Parentheses (hard)

Top Interview 150 | 22. Generate Parentheses Design Gurus Educative.io

Problem Statement

For a given number ‘N’, write a function to generate all combination of ‘N’ pairs of balanced parentheses.

Example 1:

1
2
Input: N=2
Output: (()), ()()

Example 2:

1
2
Input: N=3
Output: ((())), (()()), (())(), ()(()), ()()()

Constraints:

  • 1 <= n <= 8

Solution

This problem follows the Subsets pattern and can be mapped to Permutations. We can follow a similar BFS approach.

Let’s take Example-2 mentioned above to generate all the combinations of balanced parentheses. Following a BFS approach, we will keep adding open parentheses ( or close parentheses ). At each step we need to keep two things in mind:

  • We can’t add more than ‘N’ open parenthesis.
  • To keep the parentheses balanced, we can add a close parenthesis ) only when we have already added enough open parenthesis (. For this, we can keep a count of open and close parenthesis with every combination.

Following this guideline, let’s generate parentheses

for N=3:

  1. Start with an empty combination: “”
  2. At every step, let’s take all combinations of the previous step and add ( or ) keeping the above-mentioned two rules in mind.
  3. For the empty combination, we can add ( since the count of open parenthesis will be less than ‘N’. We can’t add ) as we don’t have an equivalent open parenthesis, so our list of combinations will now be: “(”
  4. For the next iteration, let’s take all combinations of the previous set. For “(” we can add another ( to it since the count of open parenthesis will be less than ‘N’. We can also add ) as we do have an equivalent open parenthesis, so our list of combinations will be: “((”, “()”
  5. In the next iteration, for the first combination “((”, we can add another ( to it as the count of open parenthesis will be less than ‘N’, we can also add ) as we do have an equivalent open parenthesis. This gives us two new combinations: “(((” and “(()”. For the second combination “()”, we can add another ( to it since the count of open parenthesis will be less than ‘N’. We can’t add ) as we don’t have an equivalent open parenthesis, so our list of combinations will be: “(((”, “(()”, ()(“
  6. Following the same approach, next we will get the following list of combinations: “((()”, “(()(”, “(())”, “()((”, “()()”
  7. Next we will get: “((())”, “(()()”, “(())(”, “()(()”, “()()(”
  8. Finally, we will have the following combinations of balanced parentheses: “((()))”, “(()())”, “(())()”, “()(())”, “()()()”
  9. We can’t add more parentheses to any of the combinations, so we stop here.

Here is the visual representation of this algorithm:

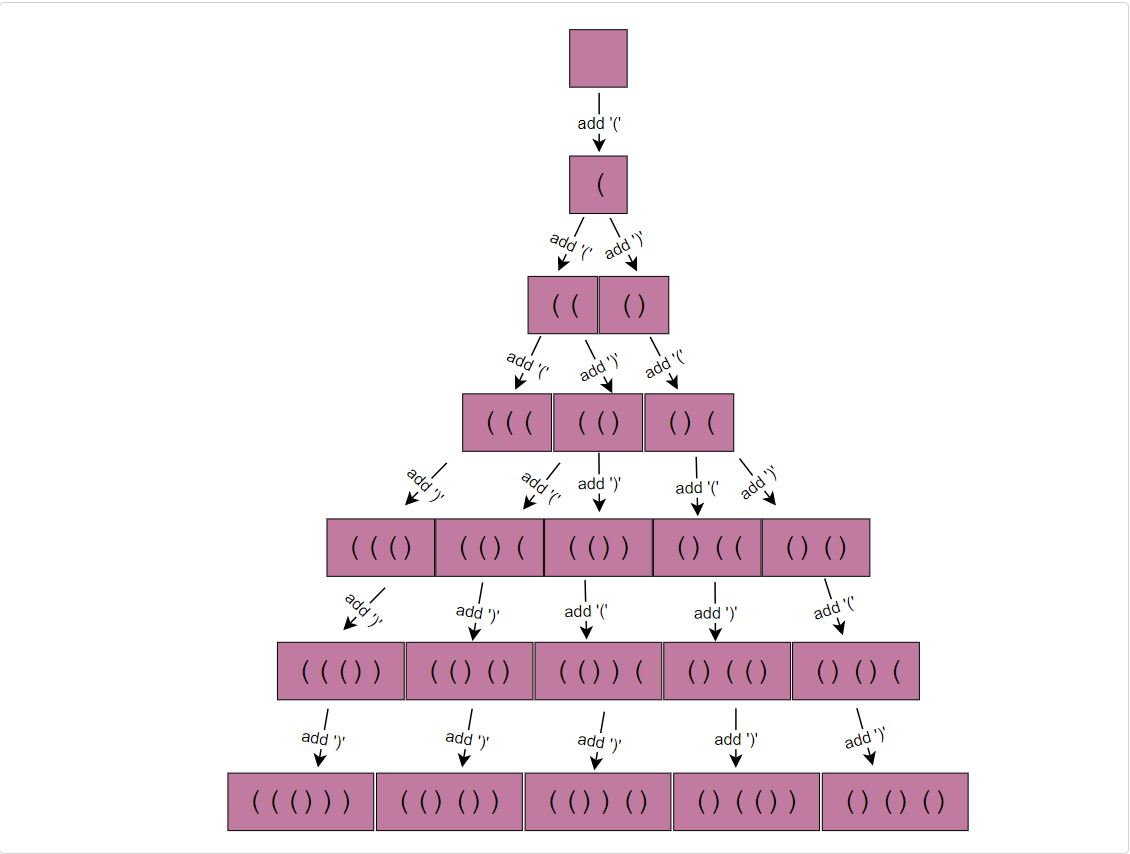
Code

Here is what our algorithm will look like:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
from collections import deque


class ParenthesesString:
    def __init__(self, str, openCount, closeCount):
        self.str = str
        self.openCount = openCount
        self.closeCount = closeCount


class Solution:
    def generateValidParentheses(self, num):
        result = []
        queue = deque()
        queue.append(ParenthesesString("", 0, 0))
        while queue:
            ps = queue.popleft()
            # if we've reached the maximum number of open and close parentheses, add to result
            if ps.openCount == num and ps.closeCount == num:
                result.append(ps.str)
            else:
                if ps.openCount < num:  # if we can add an open parentheses, add it
                    queue.append(ParenthesesString(
                        ps.str + "(", ps.openCount + 1, ps.closeCount))

                if ps.openCount > ps.closeCount:  # if we can add a close parentheses, add it
                    queue.append(ParenthesesString(ps.str + ")",
                                                   ps.openCount, ps.closeCount + 1))

        return result


def main():
    sol = Solution()
    print("All combinations of balanced parentheses are: " +
          str(sol.generateValidParentheses(2)))
    print("All combinations of balanced parentheses are: " +
          str(sol.generateValidParentheses(3)))


main()

Time complexity

Let’s try to estimate how many combinations we can have for ‘N’ pairs of balanced parentheses. If we don’t care for the ordering - that ) can only come after ( - then we have two options for every position, i.e., either put open parentheses or close parentheses. This means we can have a maximum of 2^N combinations. Because of the ordering, the actual number will be less than 2^N.

If you see the visual representation of Example-2 closely you will realize that, in the worst case, it is equivalent to a binary tree, where each node will have two children. This means that we will have 2^N leaf nodes and 2^N-1 intermediate nodes. So the total number of elements pushed to the queue will be 2^N + 2^N-1, which is asymptotically equivalent to O(2^N). While processing each element, we do need to concatenate the current string with ( or ). This operation will take O(N), so the overall time complexity of our algorithm will be O(N2^N)*. This is not completely accurate but reasonable enough to be presented in the interview.

The actual time complexity O(4n/√n)* is bounded by the Catalan number and is beyond the scope of a coding interview. See more details here.

Space complexity

All the additional space used by our algorithm is for the output list. Since we can’t have more than O(2^N) combinations, the space complexity of our algorithm is O(N \2^N)*.

Recursive Solution

Here is the recursive algorithm following a similar approach:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class Solution:
    def generateValidParenthese(self, num):
        result = []
        parenthesesString = [0 for x in range(2 * num)]
        self.generate_valid_parentheses_rec(num, 0, 0, parenthesesString, 0, result)
        return result

    def generate_valid_parentheses_rec(self, num, openCount, closeCount, parenthesesString,
                                       index, result):

        # if we've reached the maximum number of open and close parentheses, add to the result
        if openCount == num and closeCount == num:
            result.append(''.join(parenthesesString))
        else:
            if openCount < num:  # if we can add an open parentheses, add it
                parenthesesString[index] = '('
                self.generate_valid_parentheses_rec(
                    num, openCount + 1, closeCount, parenthesesString, index + 1, result)

            if openCount > closeCount:  # if we can add a close parentheses, add it
                parenthesesString[index] = ')'
                self.generate_valid_parentheses_rec(
                    num, openCount, closeCount + 1, parenthesesString, index + 1, result)


def main():
    sol = Solution()
    print("All combinations of balanced parentheses are: " +
          str(sol.generateValidParenthese(2)))
    print("All combinations of balanced parentheses are: " +
          str(sol.generateValidParenthese(3)))


main()

#Unique Generalized Abbreviations (hard)

Leetcode 320 Design Gurus Educative.io

Problem Statement

Given a word, write a function to generate all of its unique generalized abbreviations.

A generalized abbreviation of a word can be generated by replacing each substring of the word with the count of characters in the substring. Take the example of “ab” which has four substrings: “”, “a”, “b”, and “ab”. After replacing these substrings in the actual word by the count of characters, we get all the generalized abbreviations: “ab”, “1b”, “a1”, and “2”.

Note: All contiguous characters should be considered one substring, e.g., we can’t take “a” and “b” as substrings to get “11”; since “a” and “b” are contiguous, we should consider them together as one substring to get an abbreviation “2”.

Example 1:

1
2
Input: "BAT"
Output: "BAT", "BA1", "B1T", "B2", "1AT", "1A1", "2T", "3"

Example 2:

1
2
3
Input: "code"
Output: "code", "cod1", "co1e", "co2", "c1de", "c1d1", "c2e", "c3", "1ode", "1od1", "1o1e", "1o2", 
"2de", "2d1", "3e", "4"

Constraints:

  • 1 <= word.length <= 15
  • word consists of only lowercase English letters.

Solution

This problem follows the Subsets pattern and can be mapped to Balanced Parentheses. We can follow a similar BFS approach.

Let’s take Example-1 mentioned above to generate all unique generalized abbreviations. Following a BFS approach, we will abbreviate one character at a time. At each step we have two options:

  • Abbreviate the current character, or
  • Add the current character to the output and skip abbreviation.

Following these two rules, let’s abbreviate BAT:

  1. Start with an empty word: “”
  2. At every step, we will take all the combinations from the previous step and apply the two abbreviation rules to the next character.
  3. Take the empty word from the previous step and add the first character to it. We can either abbreviate the character or add it (by skipping abbreviation). This gives us two new words: _, B.
  4. In the next iteration, let’s add the second character. Applying the two rules on _ will give us _ _ and 1A. Applying the above rules to the other combination B gives us B_ and BA.
  5. The next iteration will give us: _ _ _, 2T, 1A_, 1AT, B _ _, B1T, BA_, BAT
  6. The final iteration will give us:3, 2T, 1A1, 1AT, B2, B1T, BA1, BAT

Here is the visual representation of this algorithm:

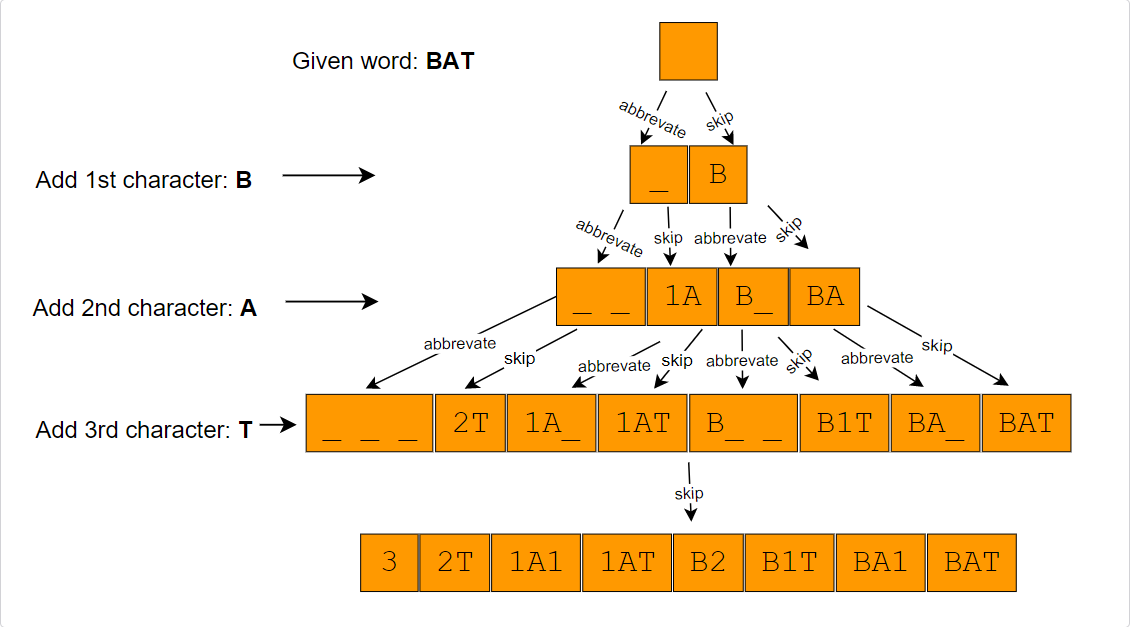
Code

Here is what our algorithm will look like:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
from collections import deque


class AbbreviatedWord:

    def __init__(self, str, start, count):
        self.str = str
        self.start = start  # 表示遍历到单词的index
        self.count = count  # 表示到目前为止有几个单词被压缩了并且还没有被处理为数字的


class Solution:
    def generateGeneralizedAbbreviation(self, word):
        wordLen = len(word)
        result = []
        queue = deque()
        queue.append(AbbreviatedWord(list(), 0, 0))
        # 这里因为对于queue中的每一个元素都要根据自己的元素属性（被压缩的字符个数），所以使用while queue作为条件
        # 而没有像之前一样使用for i in range()来循环
        while queue:
            abWord = queue.popleft()
            if abWord.start == wordLen:
                if abWord.count != 0:
                    abWord.str.append(str(abWord.count))
                result.append(''.join(abWord.str))
            else:
                # continue abbreviating by incrementing the current abbreviation count
                queue.append(AbbreviatedWord(list(abWord.str),
                                             abWord.start + 1, abWord.count + 1))

                # restart abbreviating, append the count and the current character to the string
                if abWord.count != 0:
                    abWord.str.append(str(abWord.count))

                newWord = list(abWord.str)
                newWord.append(word[abWord.start])
                queue.append(AbbreviatedWord(newWord, abWord.start + 1, 0))

        return result


def main():
    sol = Solution()
    print("Generalized abbreviation are: " +
          str(sol.generateGeneralizedAbbreviation("BAT")))
    print("Generalized abbreviation are: " +
          str(sol.generateGeneralizedAbbreviation("code")))


main()

Time complexity

Since we had two options for each character, we will have a maximum of 2^N combinations. If you see the visual representation of Example-1 closely you will realize that it is equivalent to a binary tree, where each node has two children. This means that we will have 2^N leaf nodes and 2^N-1 intermediate nodes, so the total number of elements pushed to the queue will be 2^N + 2^N-1, which is asymptotically equivalent to O(2^N). While processing each element, we do need to concatenate the current string with a character. This operation will take O(N), so the overall time complexity of our algorithm will be O(N\2^N)*.

Space complexity

All the additional space used by our algorithm is for the output list. Since we can’t have more than O(2^N) combinations, the space complexity of our algorithm is O(N2^N)*.

Recursive Solution

Here is the recursive algorithm following a similar approach:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class Solution:
    def generateGeneralizedAbbreviation(self, word):
        result = []
        self.generate_abbreviation_recursive(word, list(), 0, 0, result)
        return result

    def generate_abbreviation_recursive(self, word, abWord, start, count, result):

        if start == len(word):
            if count != 0:
                abWord.append(str(count))
            result.append(''.join(abWord))
        else:
            # continue abbreviating by incrementing the current abbreviation count
            self.generate_abbreviation_recursive(
                word, list(abWord), start + 1, count + 1, result)

            # restart abbreviating, append the count and the current character to the string
            if count != 0:
                abWord.append(str(count))
            newWord = list(abWord)
            newWord.append(word[start])
            self.generate_abbreviation_recursive(word, newWord, start + 1, 0, result)


def main():
    sol = Solution()
    print("Generalized abbreviation are: " +
          str(sol.generateGeneralizedAbbreviation("BAT")))
    print("Generalized abbreviation are: " +
          str(sol.generateGeneralizedAbbreviation("code")))


main()

*Problem Challenge 1

241. Different Ways to Add Parentheses Design Gurus Educative.io

Evaluate Expression (hard)

Given an expression containing digits and operations (+, -, *), find all possible ways in which the expression can be evaluated by grouping the numbers and operators using parentheses.

Example 1:

1
2
3
4
5
Input: "1+2*3"
Output: 7, 9
Explanation: 
  1+(2*3) => 7
  (1+2)*3 => 9

Example 2:

1
2
3
4
5
6
7
8
Input: "2*3-4-5"
Output: 8, -12, 7, -7, -3 
Explanation: 
  2*(3-(4-5)) => 8
  2*(3-4-5) => -12
  2*3-(4-5) => 7
  2*(3-4)-5 => -7
  (2*3)-4-5 => -3

Solution

This problem follows the Subsets pattern and can be mapped to Balanced Parentheses. We can follow a similar BFS approach.

Let’s take Example-1 mentioned above to generate different ways to evaluate the expression.

  1. We can iterate through the expression character-by-character.
  2. we can break the expression into two halves whenever we get an operator (+, -, *).
  3. The two parts can be calculated by recursively calling the function.
  4. Once we have the evaluation results from the left and right halves, we can combine them to produce all results.

Code

Here is what our algorithm will look like:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
class Solution:
    def diffWaysToEvaluateExpression(self, input):
        result = []
        # base case: if the input string is a number, parse and add it to output.
        if '+' not in input and '-' not in input and '*' not in input:
            result.append(int(input))
        else:
            for i in range(0, len(input)):
                char = input[i]
                if not char.isdigit():
                    # break the equation here into two parts and make recursively calls
                    leftParts = self.diffWaysToEvaluateExpression(input[0:i])
                    rightParts = self.diffWaysToEvaluateExpression(input[i + 1:])
                    for part1 in leftParts:
                        for part2 in rightParts:
                            if char == '+':
                                result.append(part1 + part2)
                            elif char == '-':
                                result.append(part1 - part2)
                            elif char == '*':
                                result.append(part1 * part2)

        return result


def main():
    sol = Solution()
    print("Expression evaluations: " +
          str(sol.diffWaysToEvaluateExpression("1+2*3")))

    print("Expression evaluations: " +
          str(sol.diffWaysToEvaluateExpression("2*3-4-5")))


main()

Time complexity

The time complexity of this algorithm will be exponential and will be similar to Balanced Parentheses. Estimated time complexity will be O(N\2^N)* but the actual time complexity O(4n/√n) is bounded by the Catalan number and is beyond the scope of a coding interview. See more details here.

Space complexity

The space complexity of this algorithm will also be exponential, estimated at O(2^N) though the actual will be O(4n/√n).

Memoized version

The problem has overlapping subproblems, as our recursive calls can be evaluating the same sub-expression multiple times. To resolve this, we can use memoization and store the intermediate results in a HashMap. In each function call, we can check our map to see if we have already evaluated this sub-expression before. Here is the memoized version of our algorithm; please see highlighted changes:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
class Solution:
    def diffWaysToEvaluateExpression(self, input):
        return self.diff_ways_to_evaluate_expression_rec({}, input)

    def diff_ways_to_evaluate_expression_rec(self, map, input):
        if input in map:
            return map[input]

        result = []
        # base case: if the input string is a number, parse and return it.
        if '+' not in input and '-' not in input and '*' not in input:
            result.append(int(input))
        else:
            for i in range(0, len(input)):
                char = input[i]
                if not char.isdigit():
                    # break the equation here into two parts and make recursively calls
                    leftParts = self.diff_ways_to_evaluate_expression_rec(
                        map, input[0:i])
                    rightParts = self.diff_ways_to_evaluate_expression_rec(
                        map, input[i + 1:])
                    for part1 in leftParts:
                        for part2 in rightParts:
                            if char == '+':
                                result.append(part1 + part2)
                            elif char == '-':
                                result.append(part1 - part2)
                            elif char == '*':
                                result.append(part1 * part2)

        map[input] = result
        return result


def main():
    sol = Solution()
    print("Expression evaluations: " +
          str(sol.diffWaysToEvaluateExpression("1+2*3")))

    print("Expression evaluations: " +
          str(sol.diffWaysToEvaluateExpression("2*3-4-5")))


main()

Problem Challenge 2

95. Unique Binary Search Trees II Design Gurus Educative.io

Structurally Unique Binary Search Trees (hard)

Given a number ‘n’, write a function to return all structurally unique Binary Search Trees (BST) that can store values 1 to ‘n’?

Example 1:

1
2
3
Input: 2
Output: 2
Explanation: Here are all the structurally unique BSTs storing all numbers from 1 to 2:

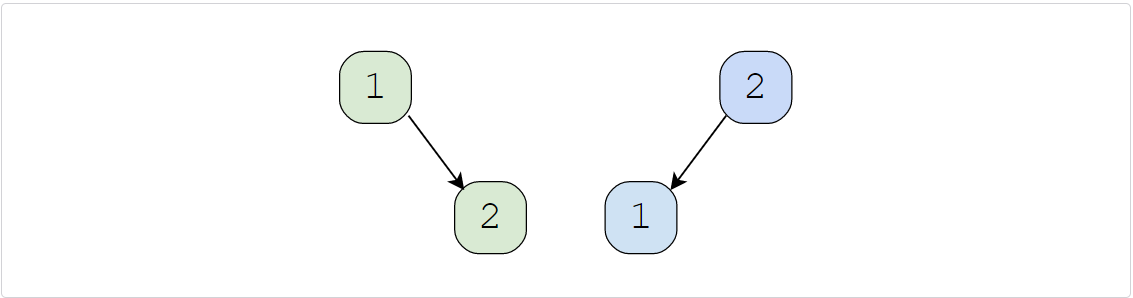
Example 2:

1
2
3
Input: 3
Output: 5
Explanation: Here are all the structurally unique BSTs storing all numbers from 1 to 3:

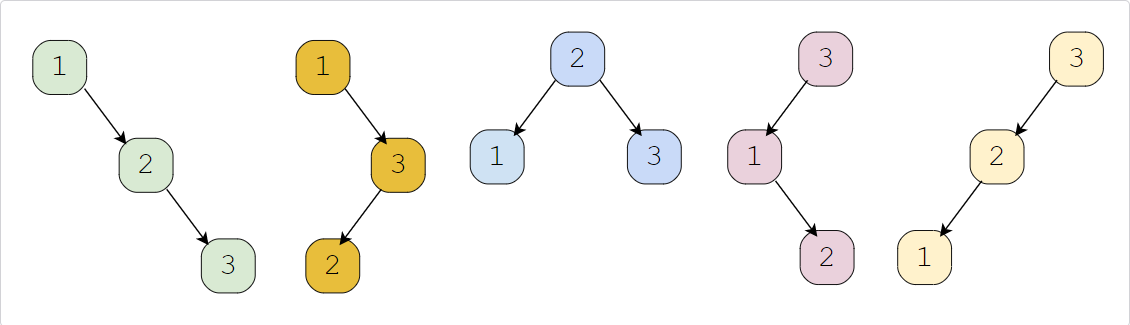
Constraints:

  • 1 <= n <= 19

Solution

This problem follows the Subsets pattern and is quite similar to Evaluate Expression. Following a similar approach, we can iterate from 1 to ‘n’ and consider each number as the root of a tree. All smaller numbers will make up the left sub-tree and bigger numbers will make up the right sub-tree. We will make recursive calls for the left and right sub-trees

Code

Here is what our algorithm will look like:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
# class TreeNode:
#   def __init__(self, val):
#     self.val = val
#     self.left = None
#     self.right = None


class Solution:
    def findUniqueTrees(self, n):
        if n <= 0:
            return []
        return self.findUnique_trees_recursive(1, n)

    def findUnique_trees_recursive(self, start, end):
        result = []
        # base condition, return 'None' for an empty sub-tree
        # consider n = 1, in this case we will have start = end = 1, this means we should have 
        # only one tree we will have two recursive calls, findUniqueTreesRecursive(1, 0) & 
        # (2, 1) both of these should return 'None' for the left and the right child
        if start > end:
            result.append(None)
            return result

        for i in range(start, end + 1):
            # making 'i' the root of the tree
            leftSubtrees = self.findUnique_trees_recursive(start, i - 1)
            rightSubtrees = self.findUnique_trees_recursive(i + 1, end)
            for leftTree in leftSubtrees:
                for rightTree in rightSubtrees:
                    root = TreeNode(i)
                    root.left = leftTree
                    root.right = rightTree
                    result.append(root)

        return result


def main():
    sol = Solution()
    print("Total trees: " + str(len(sol.findUniqueTrees(2))))
    print("Total trees: " + str(len(sol.findUniqueTrees(3))))


main()

Time complexity

The time complexity of this algorithm will be exponential and will be similar to Balanced Parentheses. Estimated time complexity will be O(n\2^n)* but the actual time complexity O(4n/√n) is bounded by the Catalan number and is beyond the scope of a coding interview. See more details here.

Space complexity

The space complexity of this algorithm will be exponential too, estimated at O(2^n), but the actual will be O(4n/√n).

Memoized version

Since our algorithm has overlapping subproblems, can we use memoization to improve it? We could, but every time we return the result of a subproblem from the cache, we have to clone the result list because these trees will be used as the left or right child of a tree. This cloning is equivalent to reconstructing the trees, therefore, the overall time complexity of the memoized algorithm will also be the same.

Problem Challenge 3

96. Unique Binary Search Trees Design Gurus Educative.io

Count of Structurally Unique Binary Search Trees (hard)

Given a number ‘n’, write a function to return the count of structurally unique Binary Search Trees (BST) that can store values 1 to ‘n’.

Example 1:

1
2
3
Input: 2
Output: 2
Explanation: As we saw in the previous problem, there are 2 unique BSTs storing numbers from 1-2.

Example 2:

1
2
3
Input: 3
Output: 5
Explanation: There will be 5 unique BSTs that can store numbers from 1 to 5.

Constraints:

  • 1 <= n <= 8

Solution

This problem is similar to Structurally Unique Binary Search Trees. Following a similar approach, we can iterate from 1 to ‘n’ and consider each number as the root of a tree and make two recursive calls to count the number of left and right sub-trees.

Code

Here is what our algorithm will look like:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
# 这道题和上道题有一点区别，这道题只是要求返回个数就可以。
# 上一道题还要求返回对应的结构
# 这道题用上面一道题目的代码也是完全可以的,但是会空间超限
# 最后返回的数组的大小就是答案


# class TreeNode:
#   def __init__(self, val):
#     self.val = val
#     self.left = None
#     self.right = None


class Solution:
    def countTrees(self, n):
        if n <= 1:
            return 1
        count = 0
        for i in range(1, n + 1):
            # making 'i' root of the tree
            countOfLeftSubtrees = self.countTrees(i - 1)
            countOfRightSubtrees = self.countTrees(n - i)
            count += (countOfLeftSubtrees * countOfRightSubtrees)

        return count


def main():
    sol = Solution()
    print("Total trees: " + str(sol.countTrees(2)))
    print("Total trees: " + str(sol.countTrees(3)))


main()

Time complexity

The time complexity of this algorithm will be exponential and will be similar to Balanced Parentheses. Estimated time complexity will be O(n2^n)O(n∗2n) but the actual time complexity O(4n/√n)* is bounded by the Catalan number and is beyond the scope of a coding interview. See more details here.

Space complexity

The space complexity of this algorithm will be exponential too, estimated O(2^n) but the actual will be O(4n/√n).

Memoized version

Our algorithm has overlapping subproblems as our recursive call will be evaluating the same sub-expression multiple times. To resolve this, we can use memoization and store the intermediate results in a HashMap. In each function call, we can check our map to see if we have already evaluated this sub-expression before. Here is the memoized version of our algorithm, please see highlighted changes:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
# class TreeNode:
#   def __init__(self, val):
#     self.val = val
#     self.left = None
#     self.right = None


class Solution:
    def countTrees(self, n):
        return self.count_trees_rec({}, n)

    def count_trees_rec(self, map, n):
        if n in map:
            return map[n]

        if n <= 1:
            return 1
        count = 0
        for i in range(1, n + 1):
            # making 'i' the root of the tree
            countOfLeftSubtrees = self.count_trees_rec(map, i - 1)
            countOfRightSubtrees = self.count_trees_rec(map, n - i)
            count += (countOfLeftSubtrees * countOfRightSubtrees)

        map[n] = count
        return count


def main():
    sol = Solution()
    print("Total trees: " + str(sol.countTrees(2)))
    print("Total trees: " + str(sol.countTrees(3)))


main()

Author：Hasuer

Link：https://hasuer.github.io/15-pattern-subsets/index.html

Publish date：May 15th 2024, 11:19:01 am

Update date：May 28th 2024, 11:29:16 am

License：本文采用知识共享署名-非商业性使用 4.0 国际许可协议进行许可

CATALOG
  1. 1. Introduction to Subsets Pattern
  2. 2. *Subsets (easy)
    1. 2.1. Problem Statement
    2. 2.2. Solution
    3. 2.3. Code
      1. 2.3.1. Time complexity
      2. 2.3.2. Space complexity
  3. 3. Subsets With Duplicates (easy)
    1. 3.1. Problem Statement
    2. 3.2. Solution
    3. 3.3. Code
      1. 3.3.1. Time complexity
      2. 3.3.2. Space complexity
  4. 4. *Permutations (medium)
    1. 4.1. Problem Statement
    2. 4.2. Solution
    3. 4.3. Code
      1. 4.3.1. Time complexity
      2. 4.3.2. Space complexity
    4. 4.4. Recursive Solution
  5. 5. String Permutations by changing case (medium)
    1. 5.1. Problem Statement
    2. 5.2. Solution
    3. 5.3. Code
      1. 5.3.1. Time complexity
      2. 5.3.2. Space complexity
  6. 6. *Balanced Parentheses (hard)
    1. 6.1. Problem Statement
    2. 6.2. Solution
    3. 6.3. Code
      1. 6.3.1. Time complexity
      2. 6.3.2. Space complexity
    4. 6.4. Recursive Solution
  7. 7. #Unique Generalized Abbreviations (hard)
    1. 7.1. Problem Statement
    2. 7.2. Solution
    3. 7.3. Code
      1. 7.3.1. Time complexity
      2. 7.3.2. Space complexity
    4. 7.4. Recursive Solution
  8. 8. *Problem Challenge 1
    1. 8.1. Evaluate Expression (hard)
    2. 8.2. Solution
    3. 8.3. Code
      1. 8.3.1. Time complexity
      2. 8.3.2. Space complexity
    4. 8.4. Memoized version
  9. 9. Problem Challenge 2
    1. 9.1. Structurally Unique Binary Search Trees (hard)
    2. 9.2. Solution
    3. 9.3. Code
      1. 9.3.1. Time complexity
      2. 9.3.2. Space complexity
    4. 9.4. Memoized version
  10. 10. Problem Challenge 3
    1. 10.1. Count of Structurally Unique Binary Search Trees (hard)
    2. 10.2. Solution
    3. 10.3. Code
      1. 10.3.1. Time complexity
      2. 10.3.2. Space complexity
    4. 10.4. Memoized version
Total : 41
2024
2022
2021
Interview
技术笔记 Grokking-Interview-Pattern