11. Pattern Tree Depth First Search

Grokking Interview Pattern Interview

Word count: 4.9kReading time: 30 min

 2024/05/11 

Introduction

This pattern is based on the Depth First Search (DFS) technique to traverse a tree.

We will be using recursion (or we can also use a stack for the iterative approach) to keep track of all the previous (parent) nodes while traversing. This also means that the space complexity of the algorithm will be O(H), where ‘H’ is the maximum height of the tree.

Let’s jump onto our first problem to understand this pattern.

*Binary Tree Path Sum (easy)

Top Interview 150 | 112. Path Sum Design Gurus Educative.io

Problem Statement

Given a binary tree and a number ‘S’, find if the tree has a path from root-to-leaf such that the sum of all the node values of that path equals ‘S’.

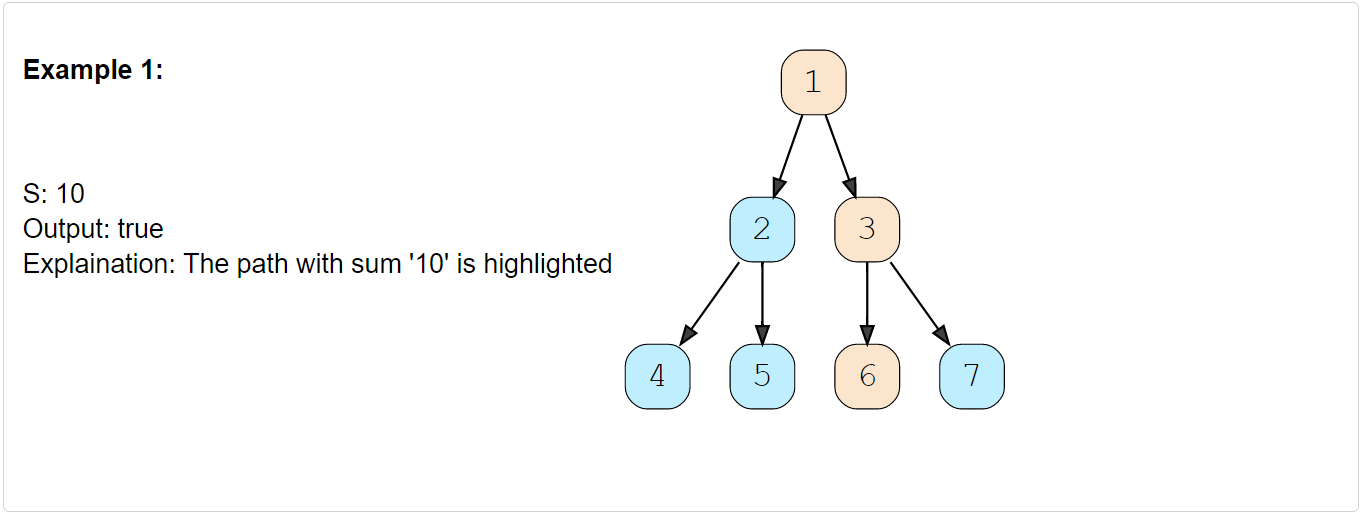
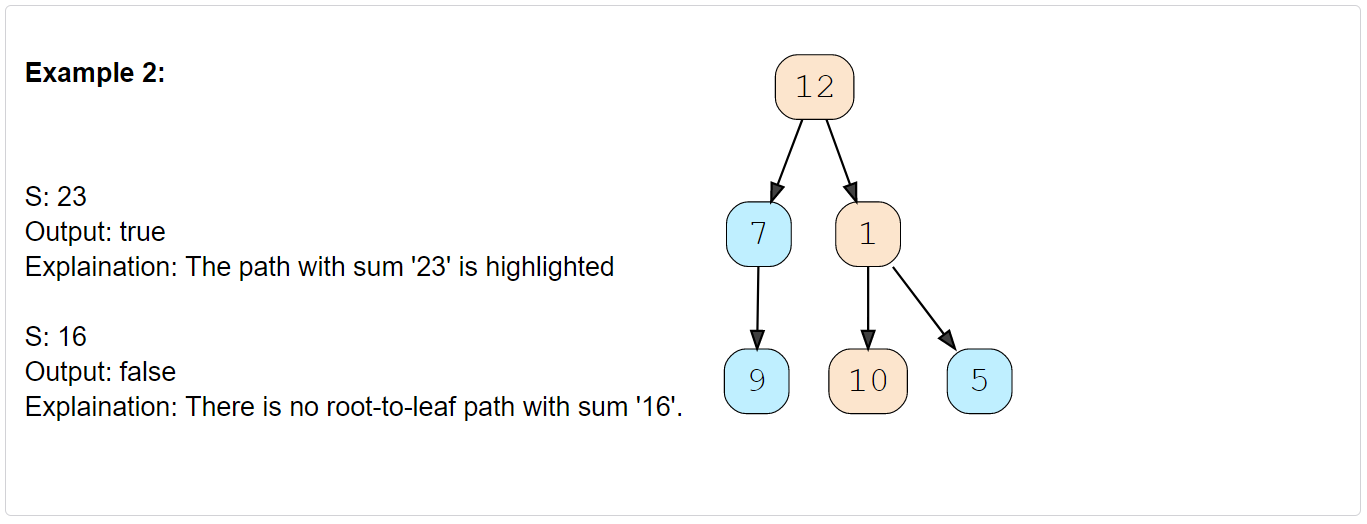
Constraints:

The number of nodes in the tree is in the range [0, 5000].
-1000 <= Node.val <= 1000
-1000 <= targetSum <= 1000

Solution

As we are trying to search for a root-to-leaf path, we can use the Depth First Search (DFS) technique to solve this problem.

To recursively traverse a binary tree in a DFS fashion, we can start from the root and at every step, make two recursive calls one for the left and one for the right child.

Here are the steps for our Binary Tree Path Sum problem:

Start DFS with the root of the tree.
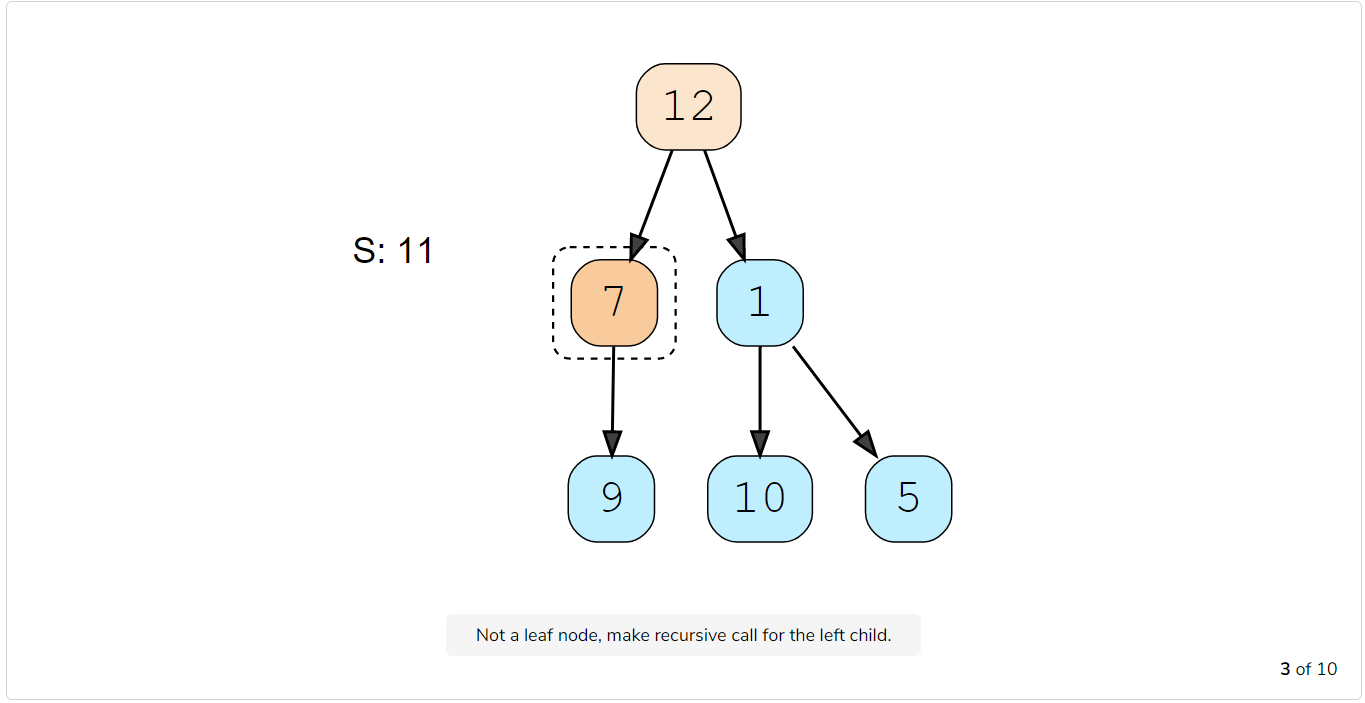
If the current node is not a leaf node, do two things:
Subtract the value of the current node from the given number to get a new sum => S = S - node.value
Make two recursive calls for both the children of the current node with the new number calculated in the previous step.
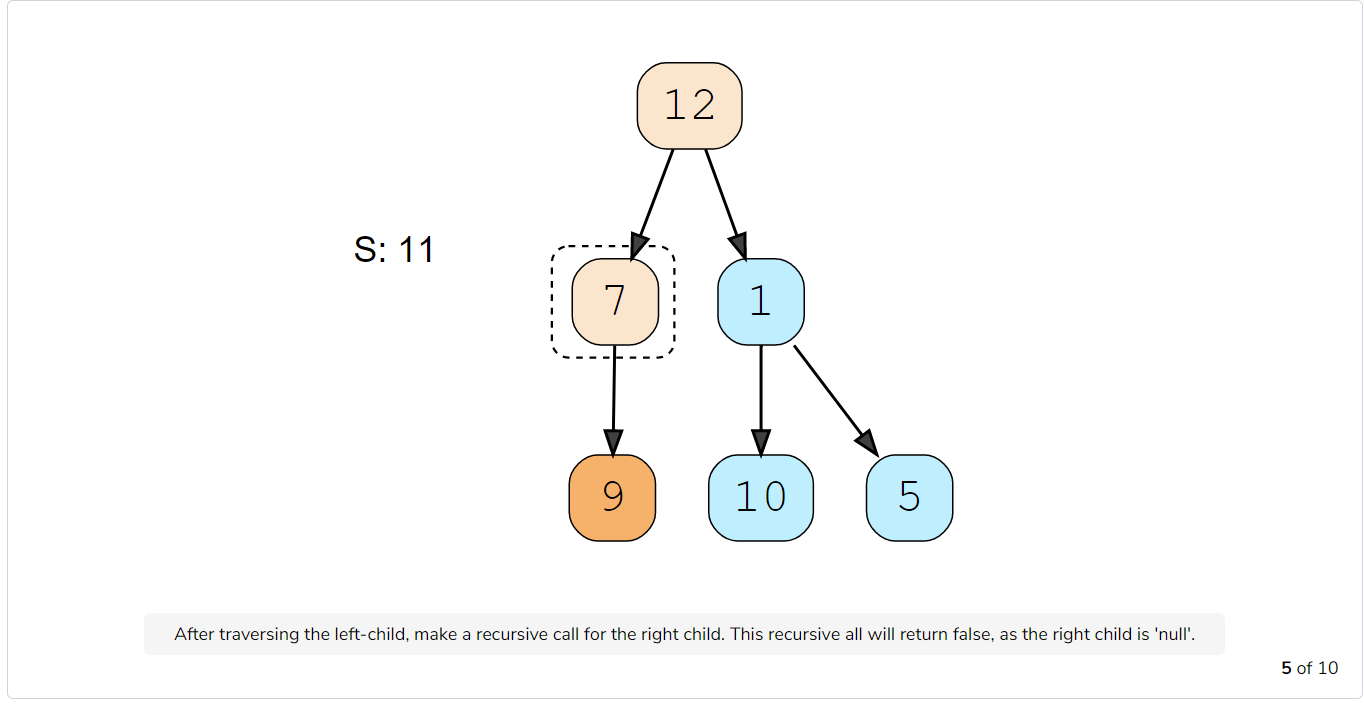
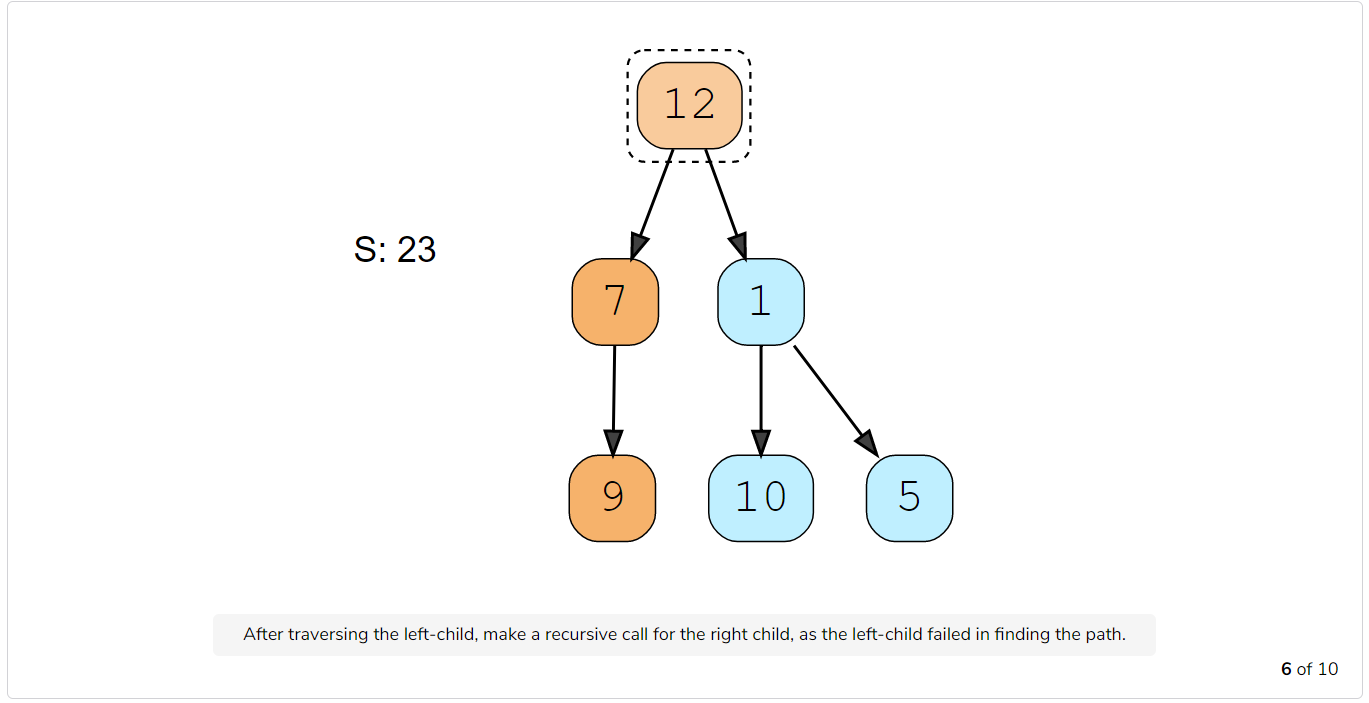
At every step, see if the current node being visited is a leaf node and if its value is equal to the given number ‘S’. If both these conditions are true, we have found the required root-to-leaf path, therefore return true.
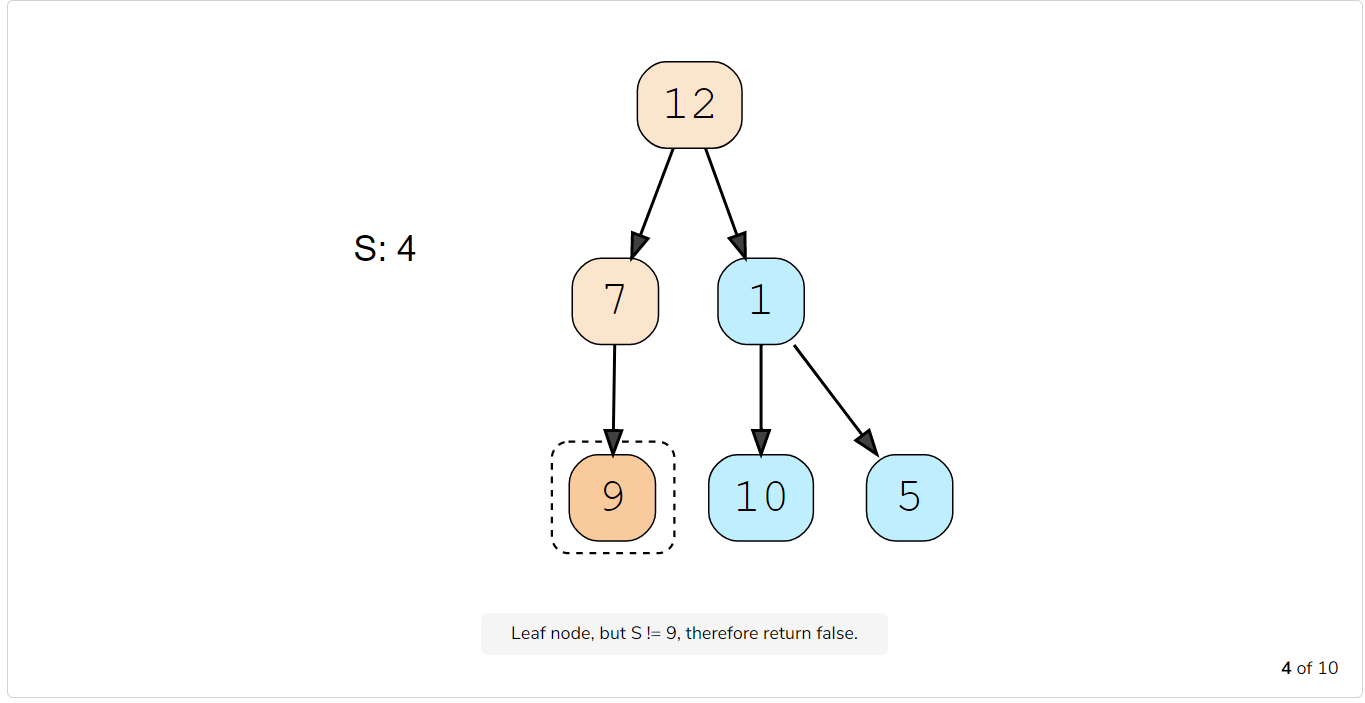
If the current node is a leaf but its value is not equal to the given number ‘S’, return false.

Let’s take the example-2 mentioned above to visually see our algorithm:

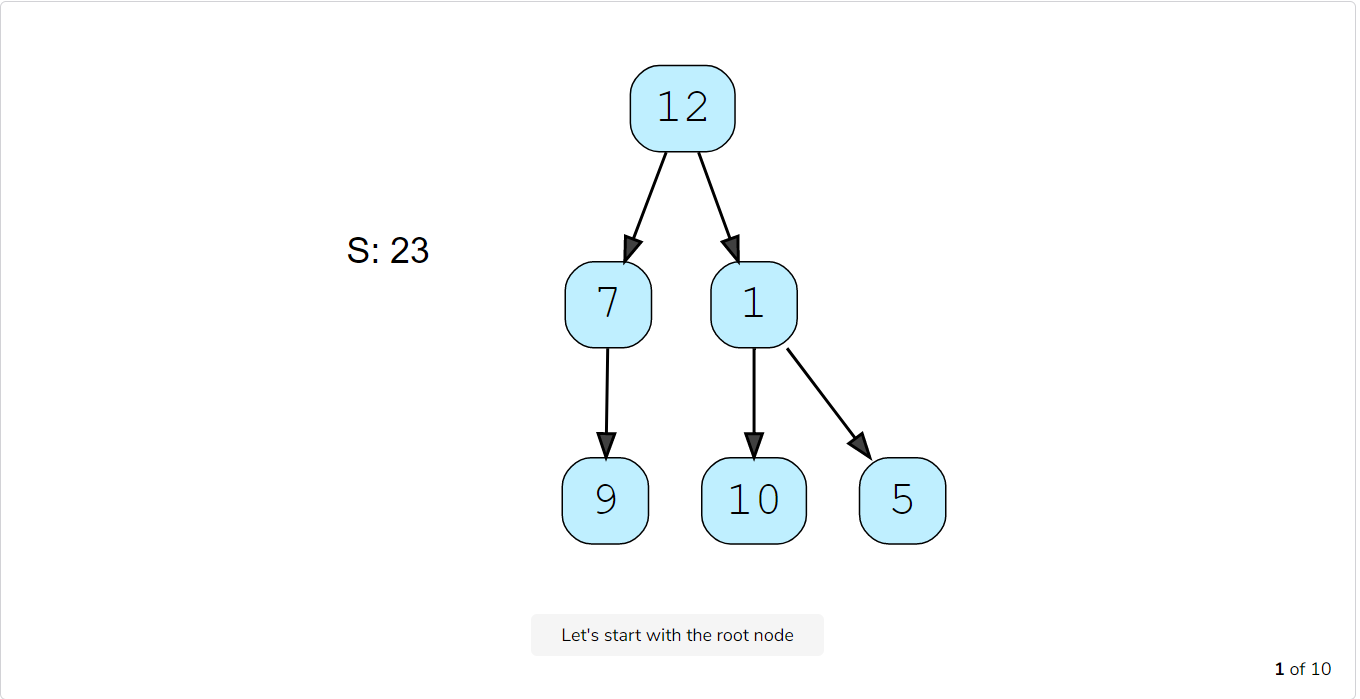
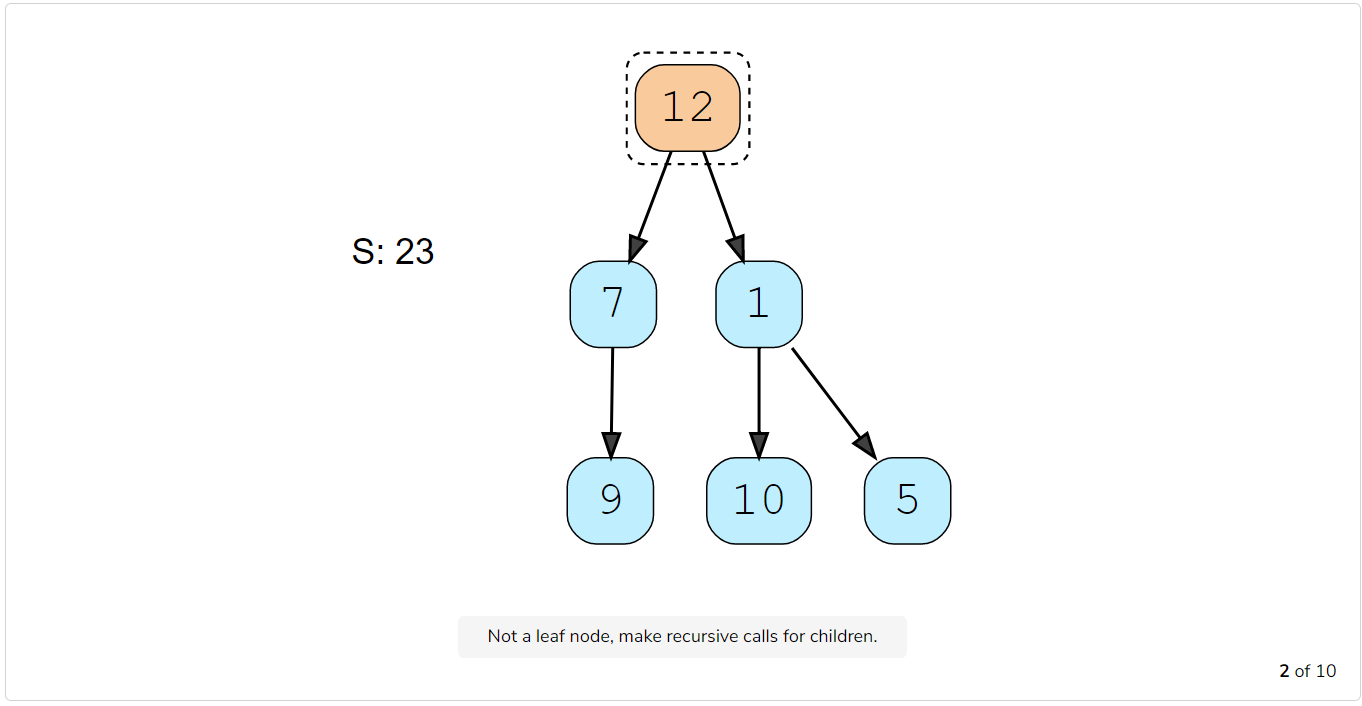
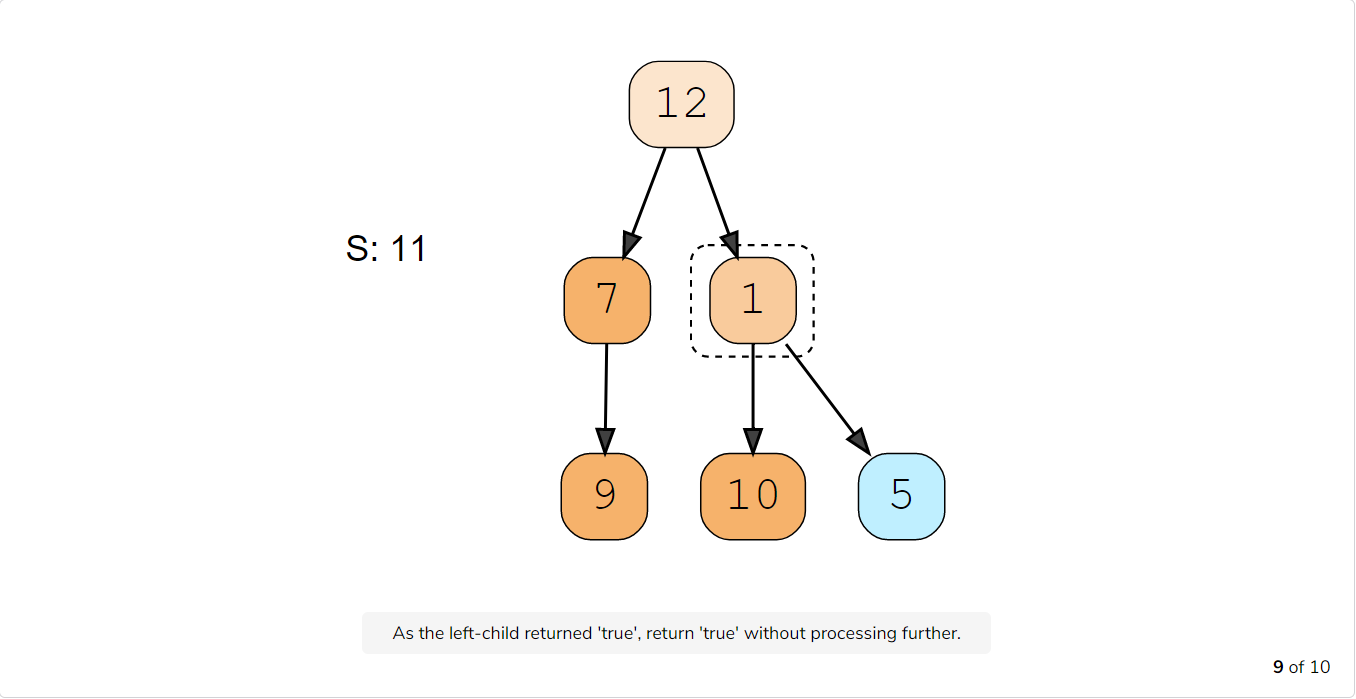
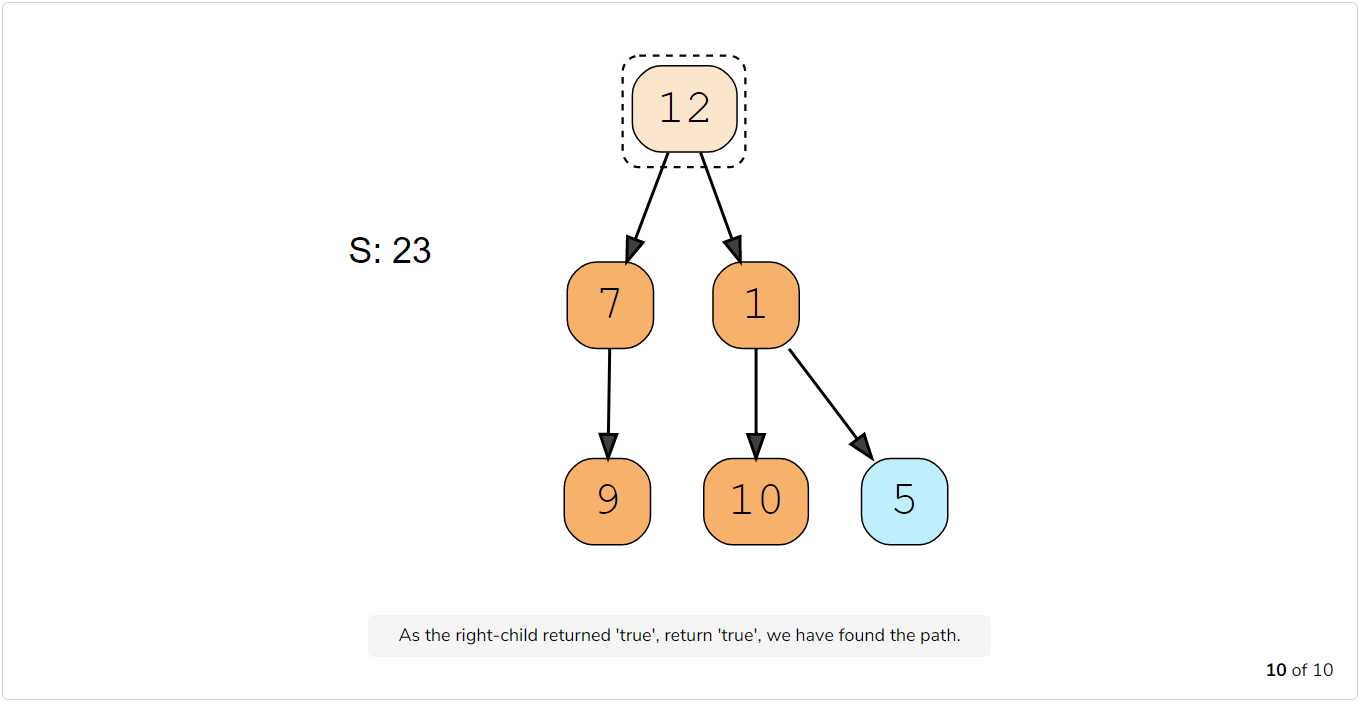
Code

Here is what our algorithm will look like:

# class TreeNode:
#   def __init__(self, val, left=None, right=None):
#     self.val = val
#     self.left = left
#     self.right = right


class Solution:
    def hasPath(self, root, sum):
        if root is None:
            return False

        # if the current node is a leaf and its value is equal to the sum, we've found a path
        if root.val == sum and root.left is None and root.right is None:
            return True

        # recursively call to traverse the left and right sub-tree
        # return true if any of the two recursive call return true
        return self.hasPath(root.left, sum - root.val) or self.hasPath(root.right, sum - root.val)


def main():
    sol = Solution()
    root = TreeNode(12)
    root.left = TreeNode(7)
    root.right = TreeNode(1)
    root.left.left = TreeNode(9)
    root.right.left = TreeNode(10)
    root.right.right = TreeNode(5)
    print("Tree has path: " + str(sol.hasPath(root, 23)))
    print("Tree has path: " + str(sol.hasPath(root, 16)))


main()

Time complexity

The time complexity of the above algorithm is O(N), where ‘N’ is the total number of nodes in the tree. This is due to the fact that we traverse each node once.

Space complexity

The space complexity of the above algorithm will be O(N) in the worst case. This space will be used to store the recursion stack. The worst case will happen when the given tree is a linked list (i.e., every node has only one child).

*All Paths for a Sum (medium)

113. Path Sum II Design Gurus Educative.io

Problem Statement

Given a binary tree and a number ‘S’, find all paths from root-to-leaf such that the sum of all the node values of each path equals ‘S’.

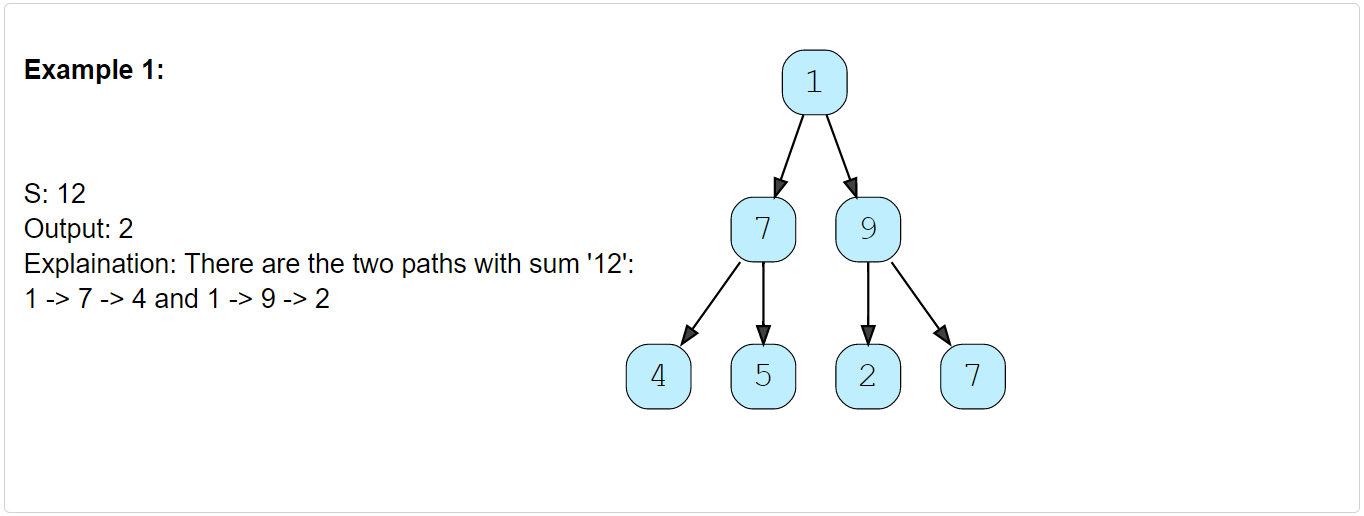
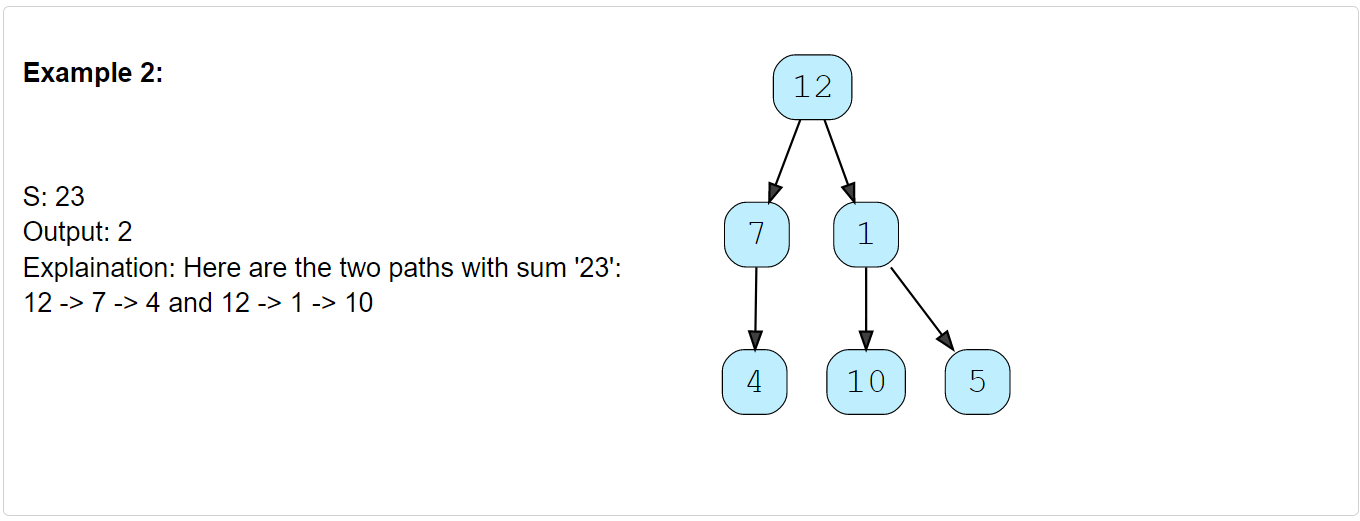
Constraints:

The number of nodes in the tree is in the range [0, 5000].
-1000 <= Node.val <= 1000
-1000 <= targetSum <= 1000

Solution

This problem follows the Binary Tree Path Sum pattern. We can follow the same DFS approach. There will be two differences:

Every time we find a root-to-leaf path, we will store it in a list.
We will traverse all paths and will not stop processing after finding the first path.

Here is the visual representation of the algorithm:

Code

Here is what our algorithm will look like:

# class TreeNode:
#   def __init__(self, val, left=None, right=None):
#     self.val = val
#     self.left = left
#     self.right = right


class Solution:
    def findPaths(self, root, required_sum):
        allPaths = []
        self.findPaths_recursive(root, required_sum, [], allPaths)
        return allPaths

    def findPaths_recursive(self, currentNode, required_sum, currentPath, allPaths):
        if currentNode is None:
            return
        # 原来以为这个if加了可以剪枝，还想着solution里怎么没有加，然后在leetcode提提交了之后出错了“[-2,null,-3]”。因为节点的值可能是负数。
        # if sum < root.val:
        #     return
        
        # add the current node to the path
        currentPath.append(currentNode.val)

        # if the current node is a leaf and its value is equal to required_sum, save the
        # current path
        if currentNode.val == required_sum and currentNode.left is None \
                and currentNode.right is None:
            allPaths.append(list(currentPath))
        else:
            # traverse the left sub-tree
            self.findPaths_recursive(currentNode.left, required_sum -
                                     currentNode.val, currentPath, allPaths)
            # traverse the right sub-tree
            self.findPaths_recursive(currentNode.right, required_sum -
                                     currentNode.val, currentPath, allPaths)

        # remove the current node from the path to backtrack,
        # we need to remove the current node while we are going up the recursive call stack.
        del currentPath[-1]


def main():
    sol = Solution()
    root = TreeNode(12)
    root.left = TreeNode(7)
    root.right = TreeNode(1)
    root.left.left = TreeNode(4)
    root.right.left = TreeNode(10)
    root.right.right = TreeNode(5)
    required_sum = 23
    print("Tree paths with required_sum " + str(required_sum) +
          ": " + str(sol.findPaths(root, required_sum)))


main()

Time complexity

The time complexity of the above algorithm is O(N^2), where ‘N’ is the total number of nodes in the tree. This is due to the fact that we traverse each node once (which will take O(N)), and for every leaf node we might have to store its path which will take O(N).

We can calculate a tighter time complexity of O(NlogN) from the space complexity discussion below.

Space complexity

If we ignore the space required for the allPaths list, the space complexity of the above algorithm will be O(N) in the worst case. This space will be used to store the recursion stack. The worst case will happen when the given tree is a linked list (i.e., every node has only one child).

How can we estimate the space used for the allPaths array? Take the example of the following balanced tree:

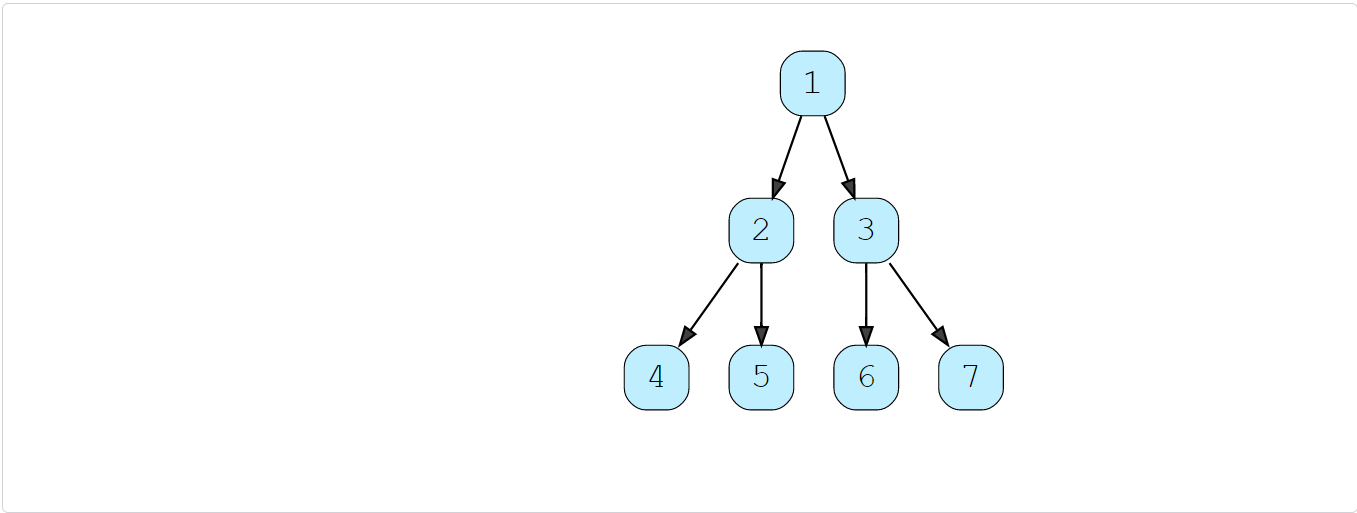
Here we have seven nodes (i.e., N = 7). Since, for binary trees, there exists only one path to reach any leaf node, we can easily say that total root-to-leaf paths in a binary tree can’t be more than the number of leaves. As we know that there can’t be more than N/2 leaves in a binary tree, therefore the maximum number of elements in allPaths will be O(N/2) = O(N). Now, each of these paths can have many nodes in them. For a balanced binary tree (like above), each leaf node will be at maximum depth. As we know that the depth (or height) of a balanced binary tree is O(logN) we can say that, at the most, each path can have logN nodes in it. This means that the total size of the allPaths list will be O(N\logN)*. If the tree is not balanced, we will still have the same worst-case space complexity.

From the above discussion, we can conclude that the overall space complexity of our algorithm is O(NlogN)*.

Also from the above discussion, since for each leaf node, in the worst case, we have to copy log(N) nodes to store its path, therefore the time complexity of our algorithm will also be O(N\logN)*.

Sum of Path Numbers (medium)

Top Interview 150 | 129. Sum Root to Leaf Numbers Design Gurus Educative.io

Problem Statement

Given a binary tree where each node can only have a digit (0-9) value, each root-to-leaf path will represent a number. Find the total sum of all the numbers represented by all paths.

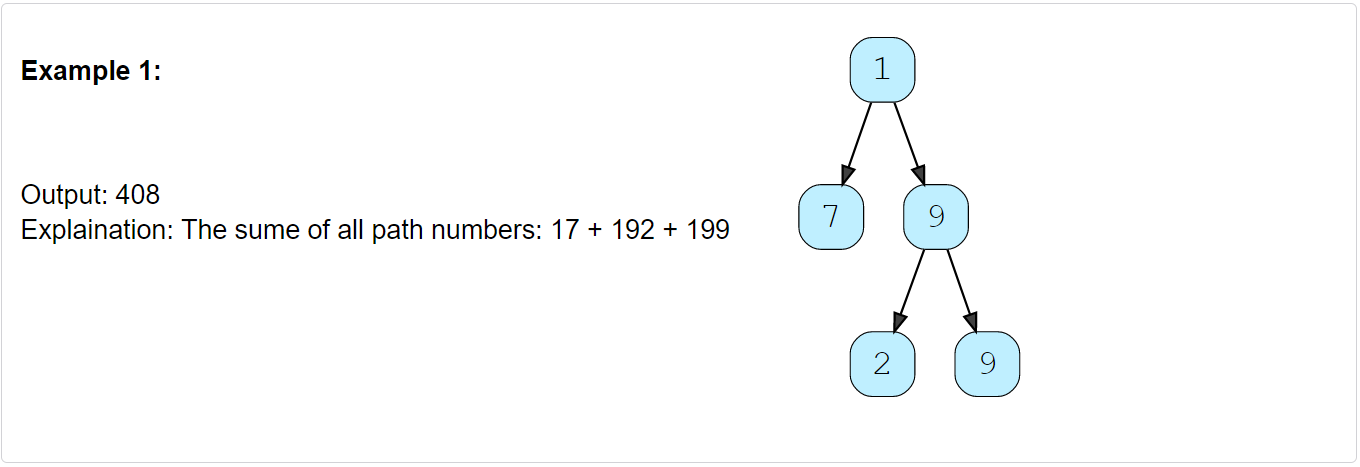
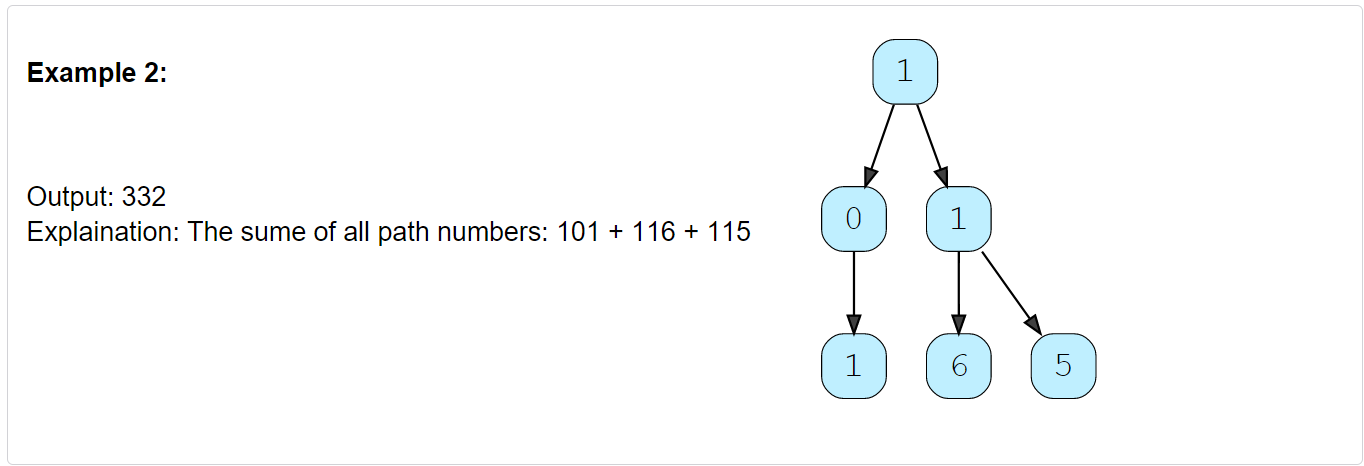
Constraints:

The number of nodes in the tree is in the range [1, 1000].
0 <= Node.val <= 9
The depth of the tree will not exceed 10.

Solution

This problem follows the Binary Tree Path Sum pattern. We can follow the same DFS approach. The additional thing we need to do is to keep track of the number representing the current path.

How do we calculate the path number for a node? Taking the first example mentioned above, say we are at node ‘7’. As we know, the path number for this node is ‘17’, which was calculated by: 1 * 10 + 7 => 17. We will follow the same approach to calculate the path number of each node.

Here is the visual representation of the algorithm:

Code

Here is what our algorithm will look like:

# class TreeNode:
#   def __init__(self, val, left=None, right=None):
#     self.val = val
#     self.left = left
#     self.right = right


class Solution:
  def findSumOfPathNumbers(self, root):
    return self.find_root_to_leaf_path_numbers(root, 0)


  def find_root_to_leaf_path_numbers(self, currentNode, pathSum):
    if currentNode is None:
      return 0

    # calculate the path number of the current node
    pathSum = 10 * pathSum + currentNode.val

    # if the current node is a leaf, return the current path sum
    if currentNode.left is None and currentNode.right is None:
      return pathSum

    # traverse the left and the right sub-tree
    return self.find_root_to_leaf_path_numbers(currentNode.left, pathSum) + \
                  self.find_root_to_leaf_path_numbers(currentNode.right, pathSum)


def main():
  sol = Solution()
  root = TreeNode(1)
  root.left = TreeNode(0)
  root.right = TreeNode(1)
  root.left.left = TreeNode(1)
  root.right.left = TreeNode(6)
  root.right.right = TreeNode(5)
  print("Total Sum of Path Numbers: " + str(sol.findSumOfPathNumbers(root)))


main()

Time complexity

The time complexity of the above algorithm is O(N), where ‘N’ is the total number of nodes in the tree. This is due to the fact that we traverse each node once.

Space complexity

*Path With Given Sequence (medium)

Design Gurus Educative.io

Problem Statement

Given a binary tree and a number sequence, find if the sequence is present as a root-to-leaf path in the given tree.

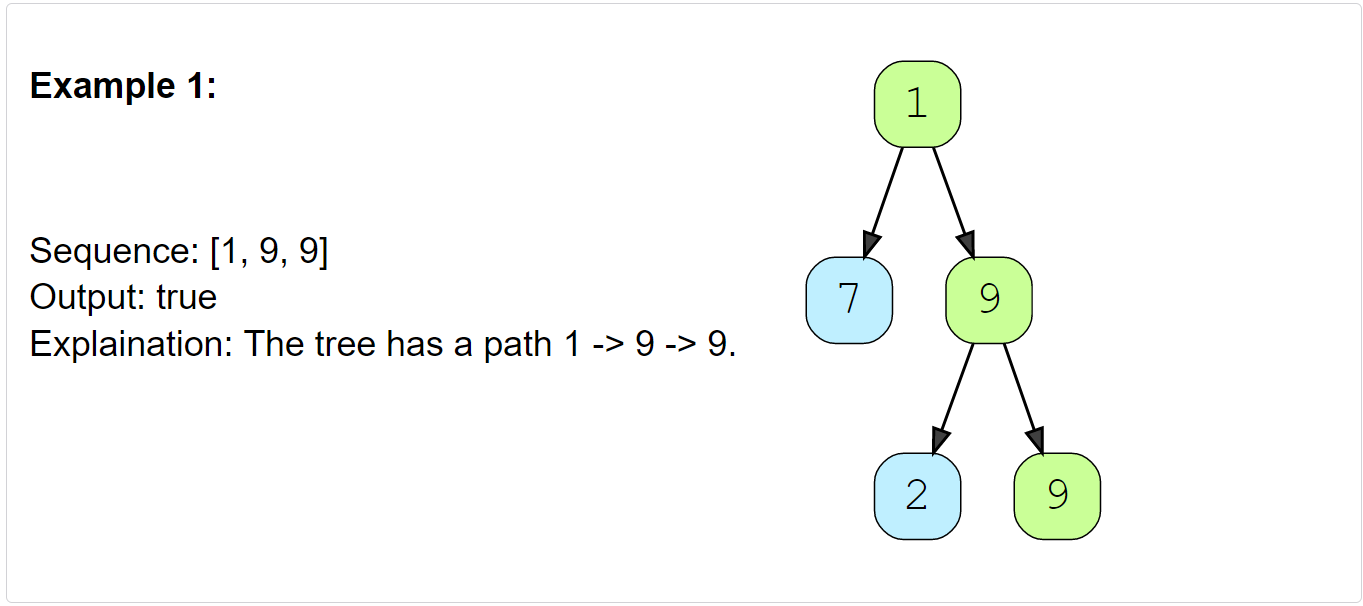
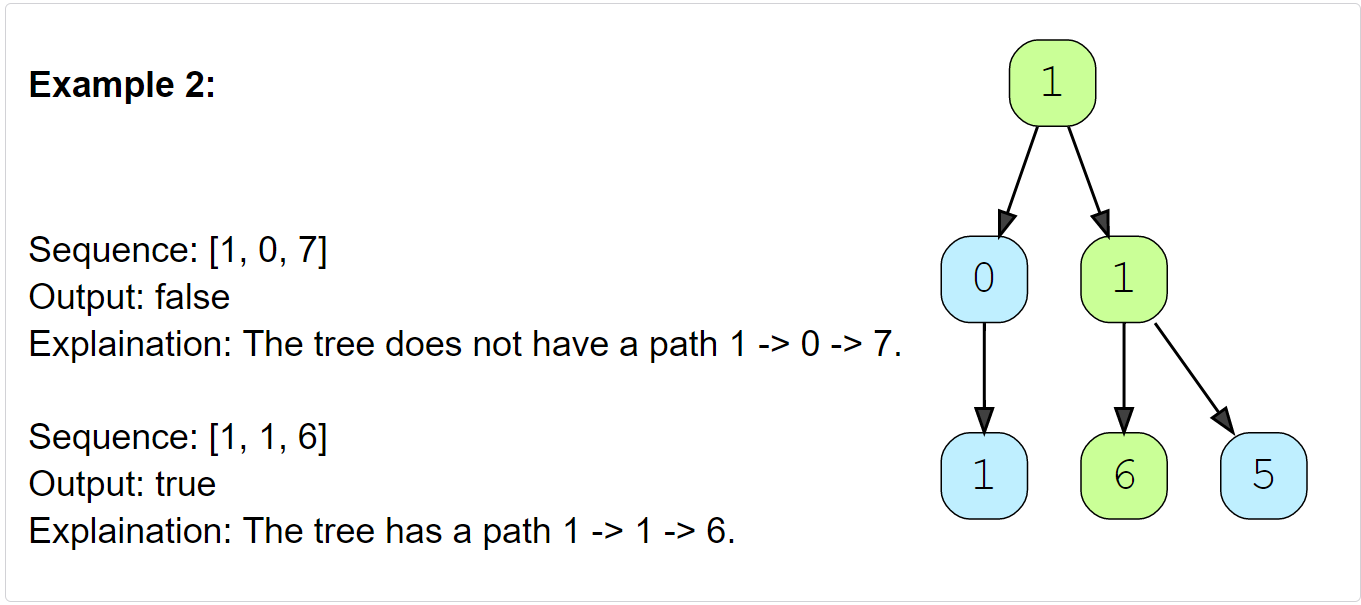
Constraints:

1 <= arr.length <= 5000
0 <= arr[i] <= 9
Each node’s value is between [0 - 9].

Solution

This problem follows the Binary Tree Path Sum pattern. We can follow the same DFS approach and additionally, track the element of the given sequence that we should match with the current node. Also, we can return false as soon as we find a mismatch between the sequence and the node value.

Here is the visual representation of the algorithm:

Code

Here is what our algorithm will look like:

# class TreeNode:
#   def __init__(self, val, left=None, right=None):
#     self.val = val
#     self.left = left
#     self.right = right


class Solution:
    def findPath(self, root, sequence):
        if not root:
            return len(sequence) == 0

        return self.find_path_recursive(root, sequence, 0)

    def find_path_recursive(self, currentNode, sequence, sequenceIndex):

        if currentNode is None:
            return False

        seqLen = len(sequence)
        if sequenceIndex >= seqLen or currentNode.val != sequence[sequenceIndex]:
            return False

        # if the current node is a leaf, add it is the end of the sequence, we have found 
        # a path!
        if currentNode.left is None and currentNode.right is None \
                and sequenceIndex == seqLen - 1:
            return True

        # recursively call to traverse the left and right sub-tree
        # return true if any of the two recursive call return true
        return self.find_path_recursive(currentNode.left, sequence, sequenceIndex + 1) or \
               self.find_path_recursive(currentNode.right, sequence, sequenceIndex + 1)


def main():
    sol = Solution()
    root = TreeNode(1)
    root.left = TreeNode(0)
    root.right = TreeNode(1)
    root.left.left = TreeNode(1)
    root.right.left = TreeNode(6)
    root.right.right = TreeNode(5)

    print("Tree has path sequence: " + str(sol.findPath(root, [1, 0, 7])))
    print("Tree has path sequence: " + str(sol.findPath(root, [1, 1, 6])))


main()

Time complexity

The time complexity of the above algorithm is O(N), where ‘N’ is the total number of nodes in the tree. This is due to the fact that we traverse each node once.

Space complexity

*Count Paths for a Sum (medium)

437. Path Sum III Design Gurus Educative.io

Problem Statement

Given a binary tree and a number ‘S’, find all paths in the tree such that the sum of all the node values of each path equals ‘S’. Please note that the paths can start or end at any node but all paths must follow direction from parent to child (top to bottom).

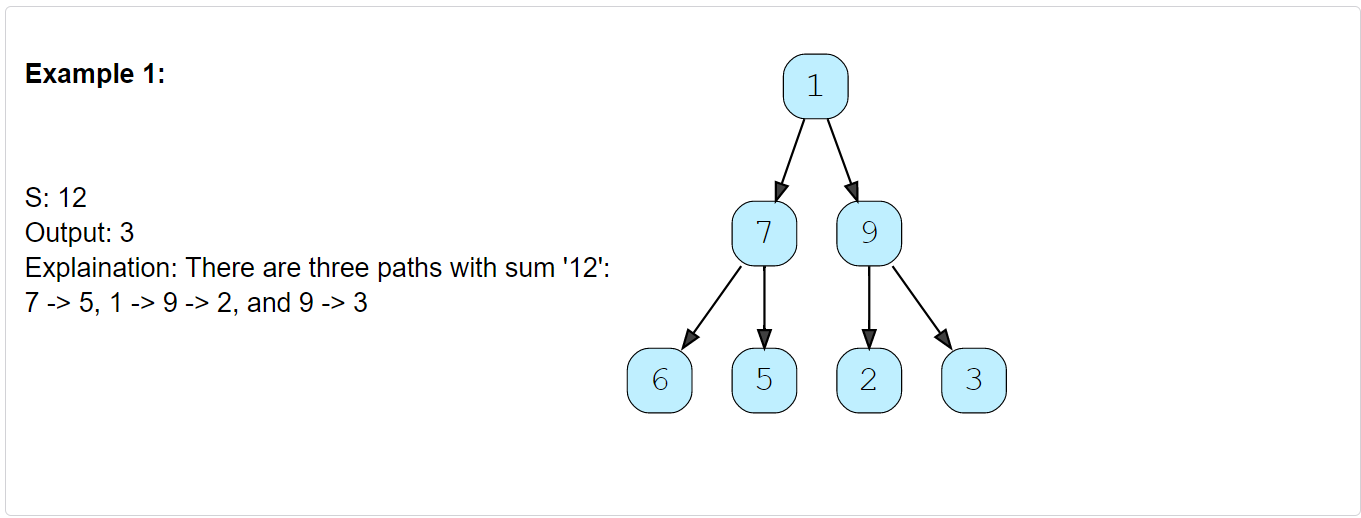
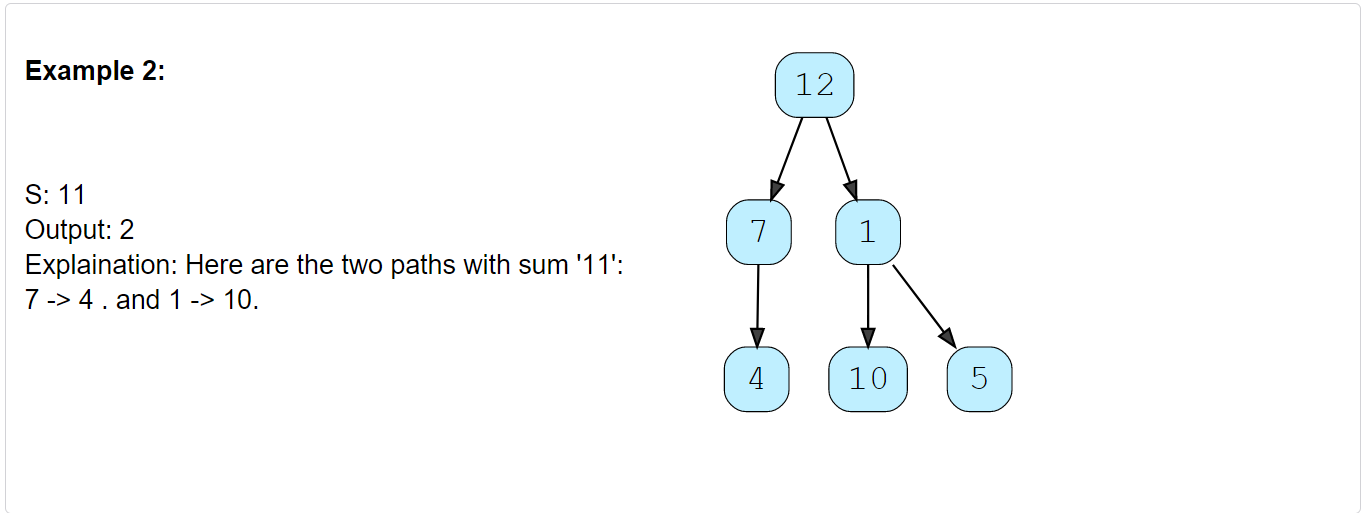
Constraints:

The number of nodes in the tree is in the range [0, 1000].
-10^9 <= Node.val <= 10^9
-1000 <= targetSum <= 1000

Solution

This problem follows the Binary Tree Path Sum pattern. We can follow the same DFS approach. But there will be four differences:

We will keep track of the current path in a list which will be passed to every recursive call.
Whenever we traverse a node we will do two things:
- Add the current node to the current path.
- As we added a new node to the current path, we should find the sums of all sub-paths ending at the current node. If the sum of any sub-path is equal to ‘S’ we will increment our path count.
We will traverse all paths and will not stop processing after finding the first path.
Remove the current node from the current path before returning from the function. This is needed to Backtrack while we are going up the recursive call stack to process other paths.

Here is the visual representation of the algorithm:

Code

Here is what our algorithm will look like:

# 也可以暴力解法：对于每一个节点都使用递归计算，可能也会TLE，具体详见下一题“problem challenge 1"
# class TreeNode:
#   def __init__(self, val, left=None, right=None):
#     self.val = val
#     self.left = left
#     self.right = right


class Solution:
    def countPaths(self, root, S):
        return self.count_paths_recursive(root, S, [])

    def count_paths_recursive(self, currentNode, S, currentPath):
        if currentNode is None:
            return 0

        # add the current node to the path
        currentPath.append(currentNode.val)
        pathCount, pathSum = 0, 0
        # find the sums of all sub-paths in the current path list
        for i in range(len(currentPath) - 1, -1, -1):
            pathSum += currentPath[i]
            # if the sum of any sub-path is equal to 'S' we increment our path count.
            if pathSum == S:
                pathCount += 1

        # traverse the left sub-tree
        pathCount += self.count_paths_recursive(currentNode.left, S, currentPath)
        # traverse the right sub-tree
        pathCount += self.count_paths_recursive(currentNode.right, S, currentPath)

        # remove the current node from the path to backtrack
        # we need to remove the current node while we are going up the recursive call stack
        del currentPath[-1]

        return pathCount


def main():
    sol = Solution()
    root = TreeNode(12)
    root.left = TreeNode(7)
    root.right = TreeNode(1)
    root.left.left = TreeNode(4)
    root.right.left = TreeNode(10)
    root.right.right = TreeNode(5)
    print("Tree has paths: " + str(sol.countPaths(root, 11)))


main()

Time complexity

The time complexity of the above algorithm is O(N^2) in the worst case, where ‘N’ is the total number of nodes in the tree. This is due to the fact that we traverse each node once, but for every node, we iterate the current path. The current path, in the worst case, can be O(N) (in the case of a skewed tree). But, if the tree is balanced, then the current path will be equal to the height of the tree, i.e., O(logN). So the best case of our algorithm will be O(NlogN).

Space complexity

The space complexity of the above algorithm will be O(N). This space will be used to store the recursion stack. The worst case will happen when the given tree is a linked list (i.e., every node has only one child). We also need O(N) space for storing the currentPath in the worst case.

Overall space complexity of our algorithm is O(N).

A more efficient solution

Can we further improve the solution?

One thing we are repeating for each node is traversing the current path and seeing if any sub-path that ends at the current node gives us the required sum.

Let’s see if we can improve this part.

We can use the Prefix Sum technique to efficiently manage the path sums.

Prefix Sum

详见Pattern Prefix sum

Let’s first understand what Prefix Sum is. For a given array, its Prefix Sum is another array where each element is the commutative sum of the corresponding element in the given array and all its previous elements.

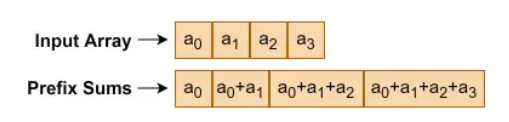
Here is an example:

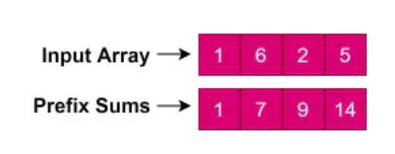
Now, let’s say we want to find all subarrays of a given array with a target sum.

Let’s say our target sum is 7, and we want to find all the subarrays of the array mentioned above.

We can clearly see that there are two such subarrays: 1) [1, 6], and 2) [2, 5].

How can we utilize the Prefix Sum array to find these two subarrays efficiently?

There are two ways Prefix Sum can help us:

a) Since each element of the prefix sum array contains the cumulative sum of current and previous elements, therefore, whenever we see our target sum, we have found our targeted subarray. For example, since the second element of the prefix sum array is 7; therefore, our target subarray will be from the start of the array till the second element, i.e., [1, 6]

(b) Secondly, the prefix sum array can also help us find our target subarray that is not starting from the first index.

If we subtract the target sum from any element of the prefix sum array, the result will also give us our target subarray (if that result is present in the prefix sum array).

For example, take the 4th element of the prefix sum array and subtract the target sum from it: 14 – 7 => 7

Is this result (7) present in the prefix sum array? Yes, it is the second element. This means the sum from the 3rd element to the current element (i.e., the 4th) is also 7.

Hence, our target subarray will be from the 3rd element to the current element, i.e., [2, 5].

Now, let’s see how we can use prefix sum for binary trees. Take the following example:

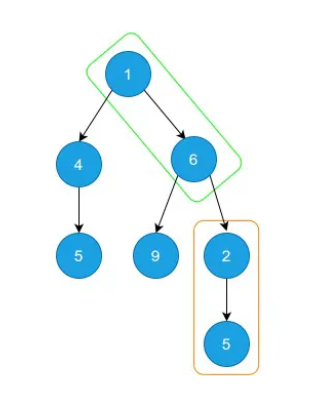
We can consider each path as an array and calculate its prefix sums to find any required sub-paths. In the above tree, the highlighted sub-paths are exactly the same as our previous array example.

Here is what our new algorithm will look like:

Code

Here is the code for this algorithm:

class TreeNode:
    def __init__(self, val, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right


class Solution:
    def count_paths(self, root, target_sum):
        # A map that stores the number of times a prefix sum has occurred so far.
        map = {}

        return self.count_paths_prefix_sum(root, target_sum, map, 0)

    def count_paths_prefix_sum(self, current_node, target_sum, map, current_path_sum):
        if current_node is None:
            return 0

        # The number of paths that have the required sum.
        path_count = 0

        # 'current_path_sum' is the prefix sum, i.e., sum of all node values from the root 
        # to the current node.
        current_path_sum += current_node.val

        # This is the base case. If the current sum is equal to the target sum, we have found 
        # a path from root to the current node having the required sum. Hence, we increment 
        # the path count by 1.
        if target_sum == current_path_sum:
            path_count += 1

        # 'current_path_sum' is the path sum from root to the current node. If within this path, 
        # there is a valid solution, then there must be an 'old_path_sum' such that:
        # => current_path_sum - old_path_sum = target_sum
        # => current_path_sum - target_sum = old_path_sum
        # Hence, we can search such an 'old_path_sum' in the map from the key 
        # 'current_path_sum - target_sum'.
        path_count += map.get(current_path_sum - target_sum, 0)

        # This is the key step in the algorithm. We are storing the number of times the prefix sum
        # `current_path_sum` has occurred so far.
        map[current_path_sum] = map.get(current_path_sum, 0) + 1

        # Counting the number of paths from the left and right subtrees.
        path_count += self.count_paths_prefix_sum(current_node.left, target_sum, map, current_path_sum)
        path_count += self.count_paths_prefix_sum(current_node.right, target_sum, map, current_path_sum)

        # Removing the current path sum from the map for backtracking.
        # 'current_path_sum' is the prefix sum up to the current node. When we go 
        # back (i.e., backtrack), then the current node is no more a part of the path, hence, we 
        # should remove its prefix sum from the map.
        map[current_path_sum] = map.get(current_path_sum, 1) - 1

        return path_count


def main():
    sol = Solution()
    root = TreeNode(12)
    root.left = TreeNode(7)
    root.right = TreeNode(1)
    root.left.left = TreeNode(4)
    root.right.left = TreeNode(10)
    root.right.right = TreeNode(5)
    print("Tree has paths: " + str(sol.count_paths(root, 11)))


main()

Time Complexity

As we are not traversing the current path for each node, the time complexity of the above algorithm will be O(N) in the worst case, where ‘N’ is the total number of nodes in the tree.

Space Complexity

The space complexity of the above algorithm will be O(N). This space will be used to store the recursion stack, as well as for the prefix sum.

*Problem Challenge 1

543. Diameter of Binary Tree Design Gurus Educative.io

Tree Diameter (medium)

Given a binary tree, find the length of its diameter. The diameter of a tree is the number of nodes on the longest path between any two leaf nodes. The diameter of a tree may or may not pass through the root.

Note: You can always assume that there are at least two leaf nodes in the given tree.

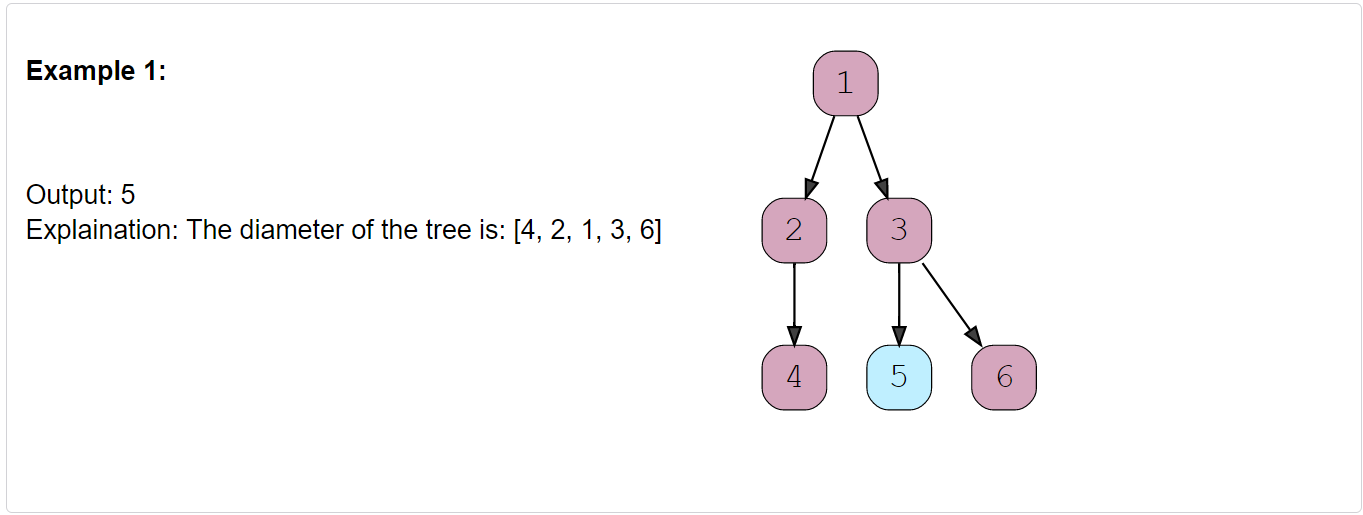
Constraints:

n == edges.length + 1
1 <= n <= 10^4
0 <= a_i, b_i < n
a_i != b_i

Solution

This problem follows the Binary Tree Path Sum pattern. We can follow the same DFS approach. There will be a few differences:

At every step, we need to find the height of both children of the current node. For this, we will make two recursive calls similar to DFS.
The height of the current node will be equal to the maximum of the heights of its left or right children, plus ‘1’ for the current node.
The tree diameter at the current node will be equal to the height of the left child plus the height of the right child plus ‘1’ for the current node: diameter = leftTreeHeight + rightTreeHeight + 1. To find the overall tree diameter, we will use a class level variable. This variable will store the maximum diameter of all the nodes visited so far, hence, eventually, it will have the final tree diameter.

Here is the visual representation of the algorithm:

Code

Here is what our algorithm will look like:

# class TreeNode:
#     def __init__(self, val, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right


class Solution:

    def findDiameter(self, root):
        self.treeDiameter = 0
        self.calculate_height(root)
        return self.treeDiameter

    def calculate_height(self, currentNode):
        if currentNode is None:
            return 0

        leftTreeHeight = self.calculate_height(currentNode.left)
        rightTreeHeight = self.calculate_height(currentNode.right)

        # if the current node doesn't have a left or right subtree, we can't have
        # a path passing through it, since we need a leaf node on each side
        if leftTreeHeight != 0 and rightTreeHeight != 0:
            # diameter at the current node will be equal to the height of left subtree +
            # the height of right sub-trees + '1' for the current node
            diameter = leftTreeHeight + rightTreeHeight + 1

            # update the global tree diameter
            self.treeDiameter = max(self.treeDiameter, diameter)

        # height of the current node will be equal to the maximum of the heights of
        # left or right subtrees plus '1' for the current node
        return max(leftTreeHeight, rightTreeHeight) + 1


def main():
    sol = Solution()
    root = TreeNode(1)
    root.left = TreeNode(2)
    root.right = TreeNode(3)
    root.left.left = TreeNode(4)
    root.right.left = TreeNode(5)
    root.right.right = TreeNode(6)
    print("Tree Diameter: " + str(sol.findDiameter(root)))
    root.left.left = None
    root.right.left.left = TreeNode(7)
    root.right.left.right = TreeNode(8)
    root.right.right.left = TreeNode(9)
    root.right.left.right.left = TreeNode(10)
    root.right.right.left.left = TreeNode(11)
    print("Tree Diameter: " + str(sol.findDiameter(root)))


main()

Time complexity

The time complexity of the above algorithm is O(N), where ‘N’ is the total number of nodes in the tree. This is due to the fact that we traverse each node once.

Space complexity

The space complexity of the above algorithm will be O(N) in the worst case. This space will be used to store the recursion stack. The worst case will happen when the given tree is a linked list (i.e., every node has only one child).

*Problem Challenge 2

Top Interview 150 | 124. Binary Tree Maximum Path Sum Design Gurus Educative.io

Path with Maximum Sum (hard)

Find the path with the maximum sum in a given binary tree. Write a function that returns the maximum sum. A path can be defined as a sequence of nodes between any two nodes and doesn’t necessarily pass through the root.

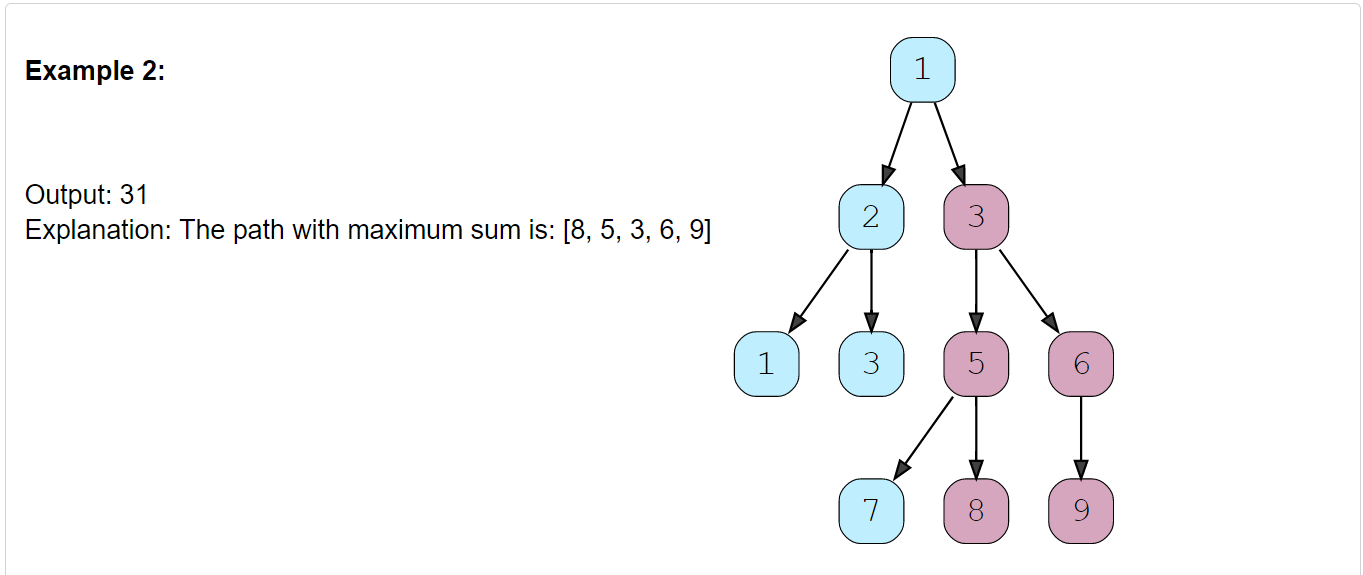
Constraints:

The number of nodes in the tree is in the range [1, 3 * 10^4].
-1000 <= Node.val <= 1000

Solution

This problem follows the Binary Tree Path Sum pattern and shares the algorithmic logic with Tree Diameter. We can follow the same DFS approach. The only difference will be to ignore the paths with negative sums. Since we need to find the overall maximum sum, we should ignore any path which has an overall negative sum.

Here is the visual representation of the algorithm:

Code

Here is what our algorithm will look like, the most important changes are in the highlighted lines:

import math


# class TreeNode:
#   def __init__(self, val, left=None, right=None):
#     self.val = val
#     self.left = left
#     self.right = right

class Solution:

    def findMaximumPathSum(self, root):
        self.globalMaximumSum = -math.inf
        self.find_maximum_path_sum_recursive(root)
        return self.globalMaximumSum

    def find_maximum_path_sum_recursive(self, currentNode):
        if currentNode is None:
            return 0

        maxPathSumFromLeft = self.find_maximum_path_sum_recursive(
            currentNode.left)
        maxPathSumFromRight = self.find_maximum_path_sum_recursive(
            currentNode.right)

        # ignore paths with negative sums, since we need to find the maximum sum we should
        # ignore any path which has an overall negative sum.
        maxPathSumFromLeft = max(maxPathSumFromLeft, 0)
        maxPathSumFromRight = max(maxPathSumFromRight, 0)

        # maximum path sum at the current node will be equal to the sum from the left 
        # subtree + the sum from right subtree + val of current node
        localMaximumSum = maxPathSumFromLeft + maxPathSumFromRight + currentNode.val

        # update the global maximum sum
        self.globalMaximumSum = max(self.globalMaximumSum, localMaximumSum)

        # maximum sum of any path from the current node will be equal to the maximum of
        # the sums from left or right subtrees plus the value of the current node
        return max(maxPathSumFromLeft, maxPathSumFromRight) + currentNode.val


def main():
    sol = Solution()
    root = TreeNode(1)
    root.left = TreeNode(2)
    root.right = TreeNode(3)

    print("Maximum Path Sum: " + str(sol.findMaximumPathSum(root)))
    root.left.left = TreeNode(1)
    root.left.right = TreeNode(3)
    root.right.left = TreeNode(5)
    root.right.right = TreeNode(6)
    root.right.left.left = TreeNode(7)
    root.right.left.right = TreeNode(8)
    root.right.right.left = TreeNode(9)
    print("Maximum Path Sum: " + str(sol.findMaximumPathSum(root)))

    root = TreeNode(-1)
    root.left = TreeNode(-3)
    print("Maximum Path Sum: " + str(sol.findMaximumPathSum(root)))


main()

Time complexity

The time complexity of the above algorithm is O(N), where ‘N’ is the total number of nodes in the tree. This is due to the fact that we traverse each node once.

Space complexity

Author：Hasuer

Link：https://hasuer.github.io/11-pattern-tree-depth-first-search/index.html

Publish date：May 11th 2024, 8:50:28 am

Update date：May 28th 2024, 11:28:30 am

License：本文采用知识共享署名-非商业性使用 4.0 国际许可协议进行许可

Next Post

12. Pattern Graphs
Previous Post

10. Pattern Tree Breadth First Search

CATALOG

1. Introduction
2. *Binary Tree Path Sum (easy)
3. *All Paths for a Sum (medium)
4. Sum of Path Numbers (medium)
5. *Path With Given Sequence (medium)
6. *Count Paths for a Sum (medium)
7. *Problem Challenge 1
8. *Problem Challenge 2

11. Pattern Tree Depth First Search

Introduction

*Binary Tree Path Sum (easy)

Problem Statement

Solution

Code

Time complexity

Space complexity

*All Paths for a Sum (medium)

Problem Statement

Solution

Code

Time complexity

Space complexity

Similar Problems

Sum of Path Numbers (medium)

Problem Statement

Solution

Code

Time complexity

Space complexity

*Path With Given Sequence (medium)

Problem Statement

Solution

Code

Time complexity

Space complexity

*Count Paths for a Sum (medium)

Problem Statement

Solution

Code

Time complexity

Space complexity

A more efficient solution

Prefix Sum

Code

Time Complexity

Space Complexity

*Problem Challenge 1

Tree Diameter (medium)

Solution

Code

Time complexity

Space complexity

*Problem Challenge 2

Path with Maximum Sum (hard)

Solution

Code

Time complexity

Space complexity