

Hasuer's Studio.

Hasuer's Studio.

7. Pattern Stack



7. Pattern Stack

Grokking Interview Pattern Interview

Word count: 7.9kReading time: 48 min

 2024/05/07   Share

• 
• 
• 
• 
• 

Introduction to Stack

Stack is a linear data structure that follows a particular order of operation. This order can either be Last In First Out (LIFO) or First In Last Out (FILO).

Imagine you have a pile of books that you plan to read. You keep adding books to the top of the pile. When you’re ready to start reading, you take a book from the top of the pile. The last book you added to the pile is the first one you read. That’s LIFO - the principle that stack data structures operate on.

What makes stacks so unique is their simplicity and elegance. Despite being straightforward, they can be incredibly powerful when used in the right way.

Real-world Examples of Stacks

Before diving into technicalities, let’s familiarize ourselves with stacks in our daily lives. Stacks are everywhere around us, even if we might not notice them. Here are some examples to help you relate:

1. Stack of Books: This is perhaps the simplest example. A pile of books is a stack. The book on the top was the last one added and will be the first one removed.
2. Stack of Plates: Picture a stack of plates at a buffet. The first plate you’ll take is the one on top, which was the last one put on the stack.
3. Web Browser History: Every time you visit a new webpage, it’s added to the top of your history stack. When you hit the back button, you’re “popping” pages off the top of the stack.
4. Undo Function in Software Applications: The undo function in software applications uses a stack to remember actions. The most recent action is on top and will be the first one undone.

Looking at these examples, it’s clear that stacks are not just a theoretical concept, but a practical one that we use unconsciously in our daily lives. With this understanding, let’s dive deeper into the operations that define stacks in data structures.

The LIFO Principle

As mentioned earlier, stacks in data structures operate on the Last-In, First-Out (LIFO) principle. This means that the last item added to the stack is the first one that gets taken out.

The LIFO principle is the heart of stack data structures. It governs how we add and remove elements, making stack operations predictable and consistent. With that, let’s explore the primary operations that you can perform on a stack.

There are four key operations that you can perform on a stack:

1. Push: This is how we add an element to the stack. The element is always added to the top.
2. Pop: This is the removal of an element from the stack. The element removed is always from the top.
3. Peek or Top: This operation allows us to see the element on the top of the stack without removing it.
4. IsEmpty: This operation checks if the stack is empty.

Let’s see these stack operations in detail in the next section.

Operations on Stack

This chapter aims to demystify the main operations involved in manipulating a stack: push, pop, peek, and isEmpty. We will examine these operations closely, detailing their functionality, providing coding examples, and highlighting their importance in problem-solving.

Push Operation

Let’s start with the push operation. As we’ve previously learned, push adds a new element to the top of the stack. Think of it like placing a new dish on top of a pile in your sink - the new dish (our data) is added to the top of the pile (our stack).

In programming, the push operation usually involves a few steps. First, we check if there’s room to add a new element (we’ll discuss this in more detail when we talk about stack overflow). If there’s room, we add the new element to the top of the stack.

Pop Operation

Next, we have the pop operation, which removes the topmost element of the stack. It’s like removing the top dish from our pile in the sink.

In code, popping an element from a stack is usually done in two parts. First, we check if there are any elements to remove (we’ll look at this more when we discuss stack underflow). If there are elements, we remove the top one.

Peek or Top Operation

The peek or top operation is slightly different. Instead of adding or removing an element, this operation allows us to look at the top element of the stack without removing it. It’s like looking at the top dish in our sink pile without touching it.

This operation can be handy when you need to know what’s on top of your stack, but you don’t want to change anything. It’s a read-only operation.

IsEmpty Operation

Finally, the isEmpty operation checks if the stack is empty. This operation is essential for preventing errors when popping an element from an empty stack (known as stack underflow).

An empty stack will return true when the isEmpty operation is performed, while a stack with one or more elements will return false.

Putting it All Together

Knowing how each of these operations works is crucial. But, what’s more important is knowing how to use them together to solve problems. Here’s a brief coding example to show how these operations can be used together.

class Stack:
    def __init__(self):
        # Initialize an empty list to represent the stack.
        self.stack = []

    def isEmpty(self):
        # Check if the stack is empty by comparing it to an empty list.
        return self.stack == []

    def push(self, data):
        # Add the given data to the top of the stack (end of the list).
        self.stack.append(data)

    def pop(self):
        if self.isEmpty():
            # If the stack is empty, return a message indicating so.
            return 'Stack is empty'
        # Remove and return the top element from the stack (last item in the list).
        return self.stack.pop()

    def peek(self):
        if self.isEmpty():
            # If the stack is empty, return a message indicating so.
            return 'Stack is empty'
        # Return the top element from the stack without removing it.
        return self.stack[-1]

Dealing with Stack Overflow and Underflow

As we discussed earlier, stack overflow and underflow are two situations you might encounter when working with stacks. Stack overflow occurs when you try to push an element onto a stack that’s already full, while stack underflow occurs when you try to pop an element from an empty stack.

Handling these situations properly is crucial to preventing runtime errors and ensuring that your code runs smoothly. Depending on the programming language and the specific implementation of the stack, you might have different ways of handling these situations. It’s always a good idea to check for stack overflow and underflow before performing push and pop operations.

Implementing Stack Data Structure

In this module, we’ll cover how to implement a stack data structure using different programming languages and data structures. This is where you’ll see how powerful, versatile, and useful stacks can be!

Stack Implementation Using an Array

Implementing a stack using an array is one of the most straightforward ways. Let’s see how you can do this in different programming languages:

class Stack:
    def __init__(self, size):
        # Initialize the stack with a specified size
        self.stack = [None] * size
        # Initialize the top pointer to -1, indicating an empty stack
        self.top = -1

    def push(self, data):
        # Check if the stack is full
        if self.top == len(self.stack) - 1:
            raise Exception('Stack is full')
        # Increment the top pointer
        self.top += 1
        # Add the data to the stack at the current top position
        self.stack[self.top] = data

    def pop(self):
        # Check if the stack is empty
        if self.isEmpty():
            raise Exception('Stack is empty')
        # Retrieve the data from the top of the stack
        data = self.stack[self.top]
        # Remove the data from the stack by setting it to None
        self.stack[self.top] = None
        # Decrement the top pointer
        self.top -= 1
        # Return the popped data
        return data

    def peek(self):
        # Check if the stack is empty
        if self.isEmpty():
            raise Exception('Stack is empty')
        # Return the data at the top of the stack without removing it
        return self.stack[self.top]

    def isEmpty(self):
        # Check if the stack is empty by examining the top pointer
        return self.top == -1

The primary advantage of using an array for implementing a stack is that it’s simple and requires no additional setup. However, the size of the array can limit the stack size, leading to a stack overflow.

Stack Implementation Using Linked List

An alternative way of implementing a stack is by using a linked list. This method can overcome the size limitation issue present in the array implementation. The code will look something like this:

class Stack:
    class Node:
        def __init__(self, data):
            self.data = data  # Store the data in this node
            self.next = None  # Initialize the next node as None

    def __init__(self):
        self.top = None  # Initialize the top of the stack as None

    def pop(self):
        if self.top is None:
            raise IndexError("pop from empty stack")  # Raise exception if the stack is empty
        item = self.top.data  # Store the top item's data
        self.top = self.top.next  # Update the top to be the next node
        return item  # Return the popped item

    def push(self, item):
        t = self.Node(item)  # Create a new node with the provided data
        t.next = self.top  # Set the next of this new node to be the current top
        self.top = t  # Update the top to be the new node

    def peek(self):
        if self.top is None:
            raise IndexError("peek from empty stack")  # Raise exception if the stack is empty
        return self.top.data  # Return the top item's data

    def is_empty(self):
        return self.top is None  # Return True if the stack is empty, False otherwise

The key difference here is that we’re using a Node class to create nodes and linking them together to form a stack. This method allows our stack to be dynamically sized, avoiding the overflow issue we saw with arrays.

Here is how different programming languages implement the stack class:

Language	API
Java	java.util.Stack
Python	Implemented through List
C++	std::stack
JavaScript	Implemented through Array

Applications of Stack

Now that we have gained a solid understanding of stack operations and their implementation, it’s time to bring it all together by exploring the real-world applications of stacks. This fascinating data structure has a multitude of uses across many different areas in computer science, from memory management and compiler design to problem-solving in data analysis. Let’s dive in!

Memory Management

One of the primary uses of stacks is in memory management. Ever wondered how your computer remembers which functions it’s running and in which order? The answer is stacks! When a function is called in a program, the system ‘pushes’ it onto a call stack. When the function finishes running, it’s ‘popped’ off the stack. This mechanism allows for nested function calls, where one function can call another.

This is also how recursion works in programming. When a function calls itself, each recursive call is added to the stack with its own set of variables. Once the base case is met, the functions start resolving and are popped off the stack one by one.

Expression Evaluation and Syntax Parsing

Another critical application of stacks is in evaluating mathematical expressions and parsing syntax in code compilers. Consider an arithmetic expression like 2 + 3 * 4. Before performing the operations, we need to check the precedence of the operators to get the correct result. Here, stacks come in handy to apply the BODMAS rule (Bracket, Order, Division and Multiplication, Addition and Subtraction).

Storing operators in a stack can help manage their execution order. Similar logic applies when compilers parse code syntax. They use stacks to check if all opening brackets have matching closing ones, which helps validate the syntax.

Undo Mechanism in Software Applications

Have you ever wondered how the ‘undo’ feature works in software applications like text editors, image editors, or even web browsers? Once again, stacks save the day. Each action you perform is pushed onto a stack. When you hit ‘undo’, the most recent action is popped from the stack and reversed. It’s a practical and elegant solution to a problem we encounter every day!

Backtracking Algorithms

Backtracking algorithms solve problems by trying out solutions and undoing them if they don’t lead to a solution. This is common in puzzles like Sudoku, the Eight Queens problem, and the Knight’s Tour problem.

In such scenarios, stacks are used to store the intermediate stages of the problem. When an attempted solution doesn’t work out, the algorithm can ‘pop’ back to a previous state and try a different path. It’s like having a ‘save game’ feature when you’re tackling a challenging puzzle!

Depth-First Search (DFS)

Stacks are also used in graph algorithms, specifically Depth-First Search (DFS). DFS explores a graph by visiting a node and recursively investigating all its unvisited neighbors. The algorithm uses a stack to remember which nodes to visit next when it finishes exploring a path.

By ‘pushing’ unvisited nodes onto the stack and ‘popping’ them once visited, DFS systematically explores every node in the graph. This method is particularly useful in network routing, AI behavior in games, and detecting cycles in a graph.

Web Page History in Browsers

Finally, an everyday example of stacks in action is web page history in a browser. When you click a link, your current page is ‘pushed’ onto a stack, and you’re taken to a new page. If you hit the ‘back’ button, your browser ‘pops’ the topmost page off the stack, taking you back to where you were. It’s a simple, intuitive way to navigate the vast expanse of the internet.

Conclusion

Through these examples, you can see just how versatile and vital stacks are in computer science and everyday applications.

Balanced Parentheses

Top Interview 150 | 20. Valid Parentheses Design Gurus

Problem Statement

Given a string s containing (, ), [, ], {, and } characters. Determine if a given string of parentheses is balanced.

A string of parentheses is considered balanced if every opening parenthesis has a corresponding closing parenthesis in the correct order.

Example 1:

Input: String s = “{[()]}”;
Expected Output: true
Explanation: The parentheses in this string are perfectly balanced. Every opening parenthesis ‘{‘, ‘[‘, ‘(‘ has a corresponding closing parenthesis ‘}’, ‘]’, ‘)’ in the correct order.

Example 2:

Input: string s = “{[}]”;
Expected Output: false
Explanation: The brackets are not balanced in this string. Although it contains the same number of opening and closing brackets for each type, they are not correctly ordered. The ‘]’ closes ‘[‘ before ‘{‘ can be closed by ‘}’, and similarly, ‘}’ closes ‘{‘ before ‘[‘ can be closed by ‘]’.

Example 3:

Input: String s = “(]”;
Expected Output: false
Explanation: The parentheses in this string are not balanced. Here, ‘)’ does not have a matching opening parenthesis ‘(‘, and similarly, ‘]’ does not have a matching opening bracket ‘[‘.

Constraints:

• 1 <= s.length <= 10^4
• s consists of parentheses only '()[]{}'.

Solution

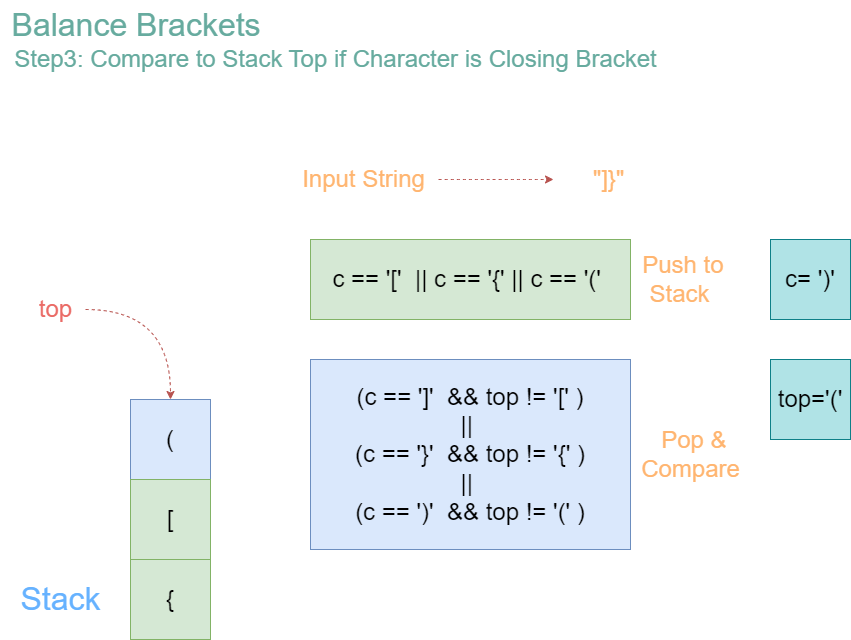
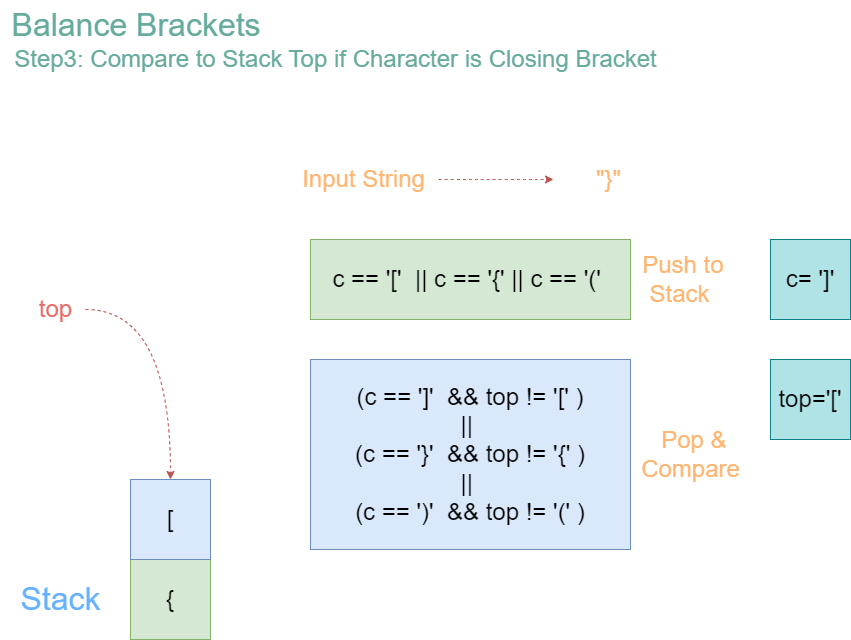
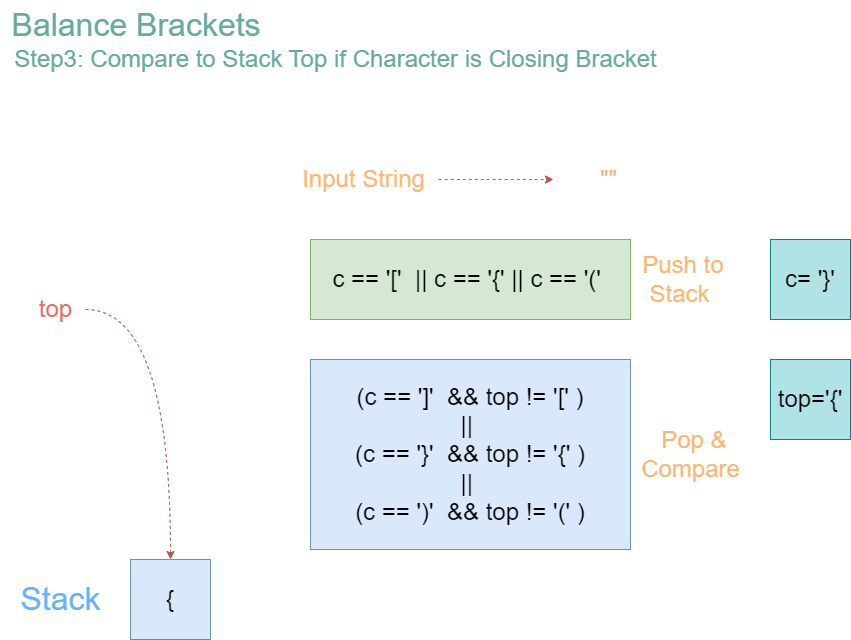
To solve this problem, we use a stack data structure. As we traverse the string, each time we encounter an opening parenthesis (‘(‘, ‘{‘, or ‘[‘), we push it onto the stack. When we find a closing parenthesis (‘)’, ‘}’, or ‘]’), we check if it matches the type of the opening parenthesis at the top of the stack. If it matches, we pop the top element from the stack; if not, or if the stack is empty when we find a closing parenthesis, the string is not balanced, and we return false.

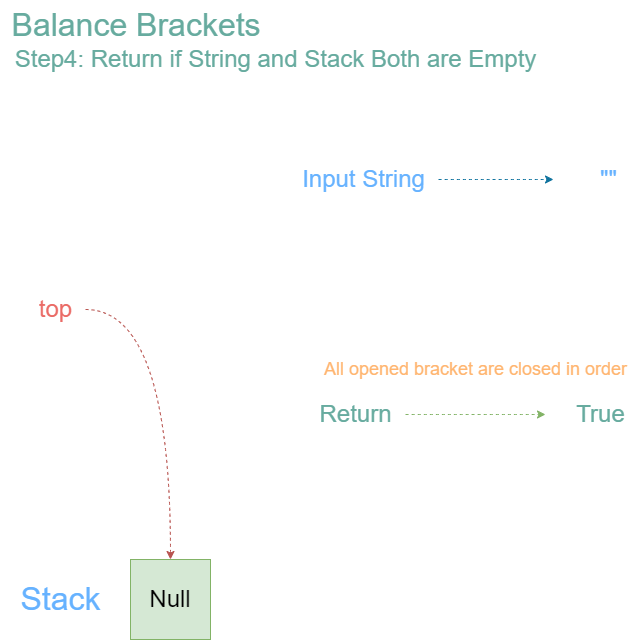
After processing the entire string, if the stack is empty, it means all parentheses were properly closed and nested, so we return true. Otherwise, we return false.

Here is a step-by-step algorithm:

1. Initialize an empty Stack.
2. Iterate over the string of parentheses.
   • If the current character is an opening parenthesis, push it onto the Stack.
   • If the current character is a closing parenthesis, check the top of the Stack.
     • If the Stack is empty, then the string is not balanced (there is a closing parenthesis without a matching opening parenthesis), so return false.
     • If the top of the Stack is the matching opening parenthesis, pop it off the Stack.
     • If the top of the Stack is not the matching opening parenthesis, then the string is not balanced, so return false.
3. After checking all parentheses, if the Stack is empty, then the string is balanced, so return true. If the Stack is not empty, then there are unmatched opening parentheses, so the string is not balanced, return false.

Algorithm Walkthrough

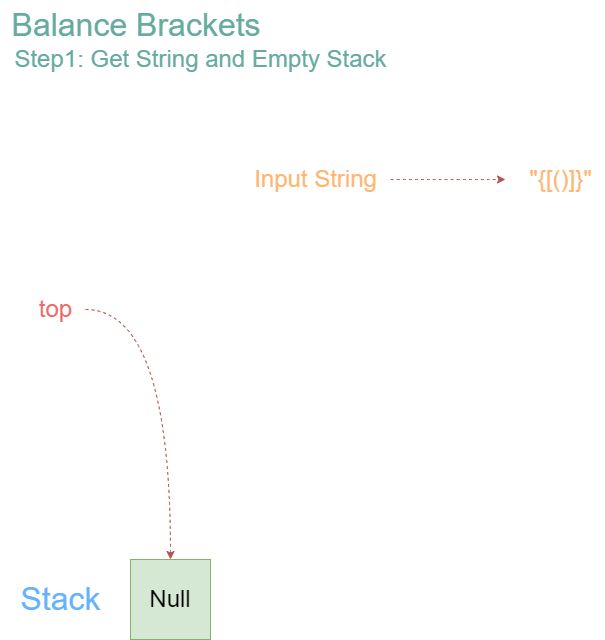
Let’s consider the input “{[()]}”, and observe how algorithm works.

Initialization:

• Start with an empty stack.

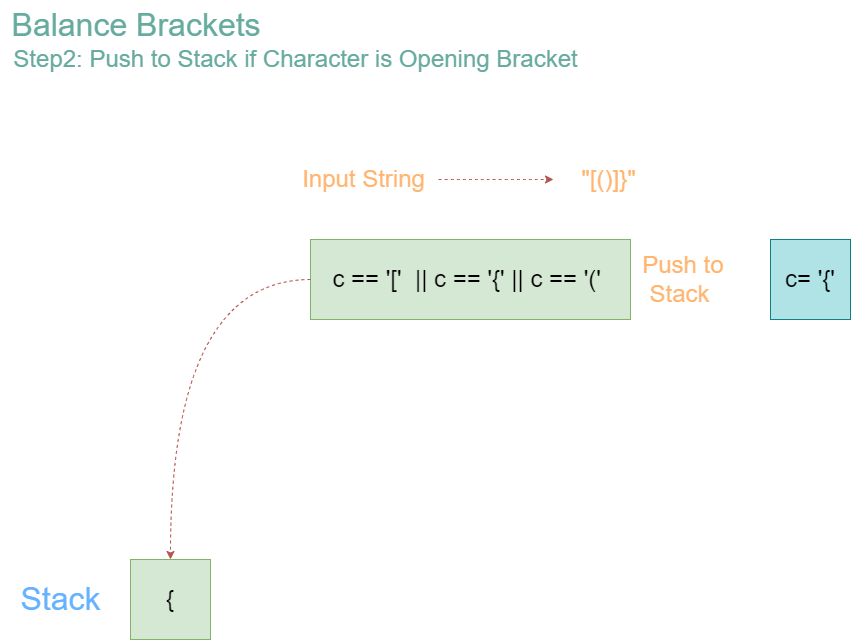
Iteration 1: Character = ‘{‘

• Stack before operation: []
• Since ‘{‘ is an opening bracket, push it onto the stack.

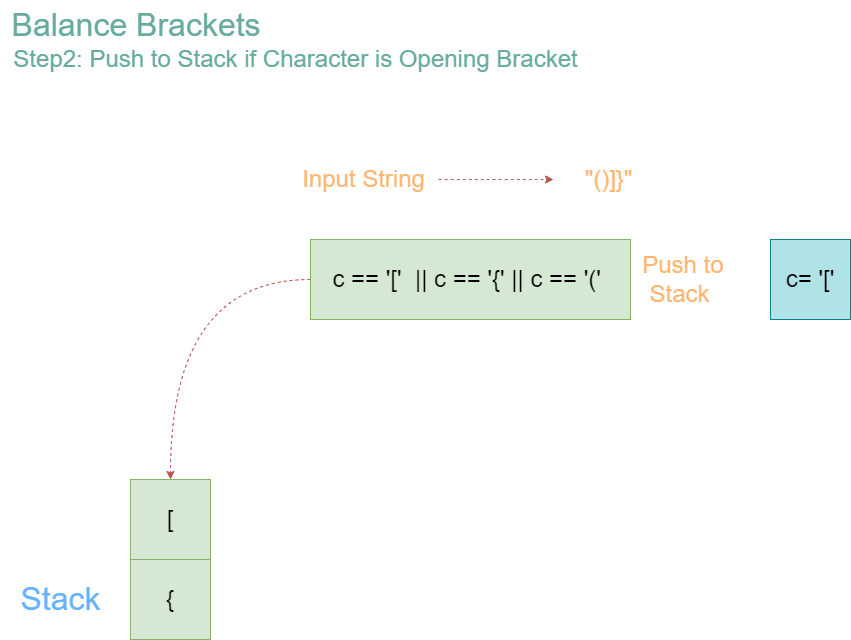
Iteration 2: Character = ‘[‘

• Stack before operation: [‘{‘]
• Since ‘[‘ is an opening bracket, push it onto the stack.

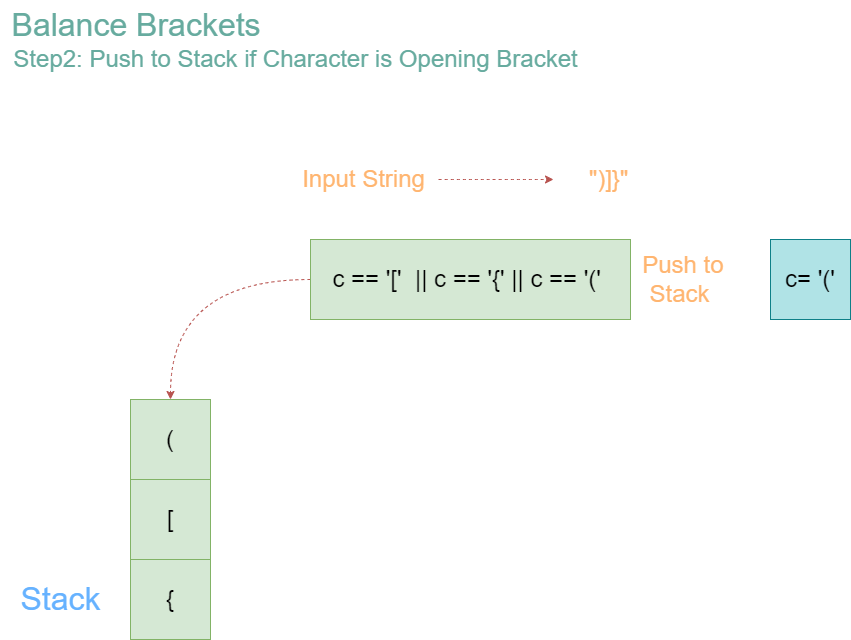
Iteration 3: Character = ‘(‘

• Stack before operation: [‘{‘, ‘[‘]
• Since ‘(‘ is an opening bracket, push it onto the stack.

Iteration 4: Character = ‘)’

• Stack before operation: [‘{‘, ‘[‘, ‘(‘]
• ‘)’ is a closing bracket. The top of the stack is ‘(‘, which is the corresponding opening bracket for ‘)’. So, pop ‘(‘ from the stack.

Iteration 5: Character = ‘]’

• Stack before operation: [‘{‘, ‘[‘]
• ‘]’ is a closing bracket. The top of the stack is ‘[‘, which is the corresponding opening bracket for ‘]’. So, pop ‘[‘ from the stack.

Iteration 6: Character = ‘}’

• Stack before operation: [‘{‘]
• ‘}’ is a closing bracket. The top of the stack is ‘{‘, which is the corresponding opening bracket for ‘}’. So, pop ‘{‘ from the stack.

Final Check:

• After processing all characters, check the stack.
• The stack is empty, indicating that all opening brackets were properly matched and closed.
• Therefore, the input string “{[()]}” is valid with properly balanced parentheses.

Code

Here is how you can implement this algorithm:

from collections import deque


class Solution:
    def isValid(self, s: str) -> bool:
        # Creating a stack to keep track of opening parentheses
        stack = deque()
        # stack = [] # 原版，但是我比较习惯deque,而且不会对时间和空间复杂度有影响

        # Iterating through each character in the input string
        for c in s:
            # If the character is an opening parenthesis, push it onto the stack
            if c in ['(', '{', '[']:
                stack.append(c)
            else:
                # If stack is empty and we have a closing parenthesis, the string is not balanced
                if not stack:
                    return False

                # Pop the top character from the stack
                top = stack.pop()

                # If the character is a closing parenthesis, check whether
                # it corresponds to the most recent opening parenthesis
                if c == ')' and top != '(':
                    return False
                if c == '}' and top != '{':
                    return False
                if c == ']' and top != '[':
                    return False
        # If the stack is empty, all opening parentheses had a corresponding closing match
        return not stack


# Test cases to verify the solution
sol = Solution()
test1 = "{[()]}";  # Should be valid
test2 = "{[}]";  # Should be invalid
test3 = "(]";  # Should be invalid

print("Test 1:", sol.isValid(test1))
print("Test 2:", sol.isValid(test2))
print("Test 3:", sol.isValid(test3))

Time and Space Complexity Analysis

The time complexity of this algorithm is O(n), where n is the length of the string. This is because we’re processing each character in the string exactly once.

The space complexity is also O(n) in the worst-case scenario when all the characters in the string are opening parentheses, so we push each character onto the Stack. In the average case, however, the space complexity would be less than O(n).

Reverse a String

344. Reverse String Design Gurus

Problem Statement

Given a string, write a function that uses a stack to reverse the string. The function should return the reversed string.

Examples

Example 1:

Input: "Hello, World!"
Output: "!dlroW ,olleH"

Example 2:

Input: "OpenAI"
Output: "IAnepO"

Example 3:

Input: "Stacks are fun!"
Output: "!nuf era skcatS"

Constraints:

• 1 <= s.length <= 10^5
• s[i] is a printable ascii character.

Solution

The solution to reverse a string can be elegantly achieved using a stack. The algorithm involves pushing each character of the string onto a stack and then popping them off, which naturally reverses their order. As we iterate through the string, each character is added to the top of the stack.

Once the entire string has been processed, we remove the characters from the stack one by one and append them to a new string. This process ensures that the characters are appended in reverse order, as the last character pushed onto the stack will be the first to be popped off. This method efficiently reverses the string while maintaining the integrity of the original data.

Here is the step-by-step algorithm.

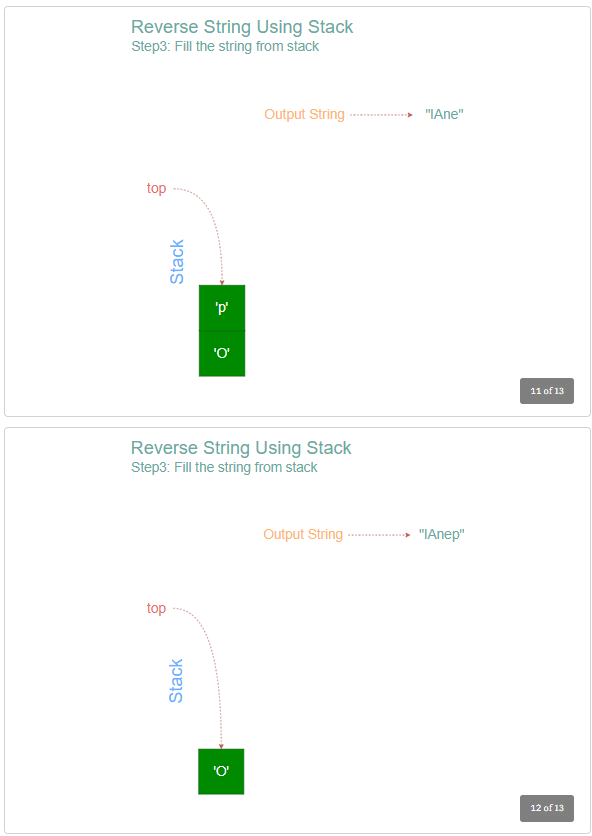
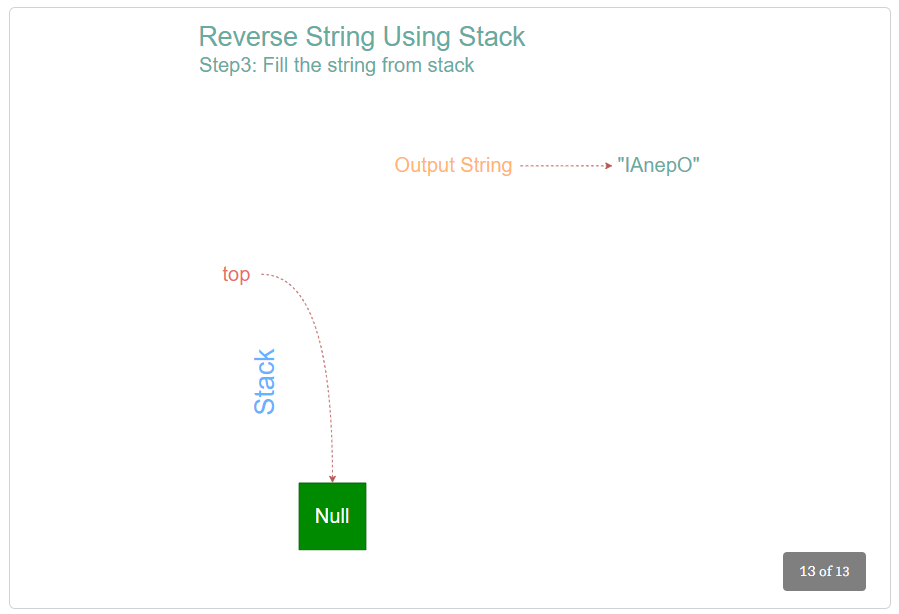
1. Initialize an empty stack.
2. For each character in the input string, push the character into the stack.
3. Initialize an empty string to hold the reversed string.
4. While the stack is not empty, pop out the top character from the stack and append it to the reversed string.
5. Finally, return the reversed string.

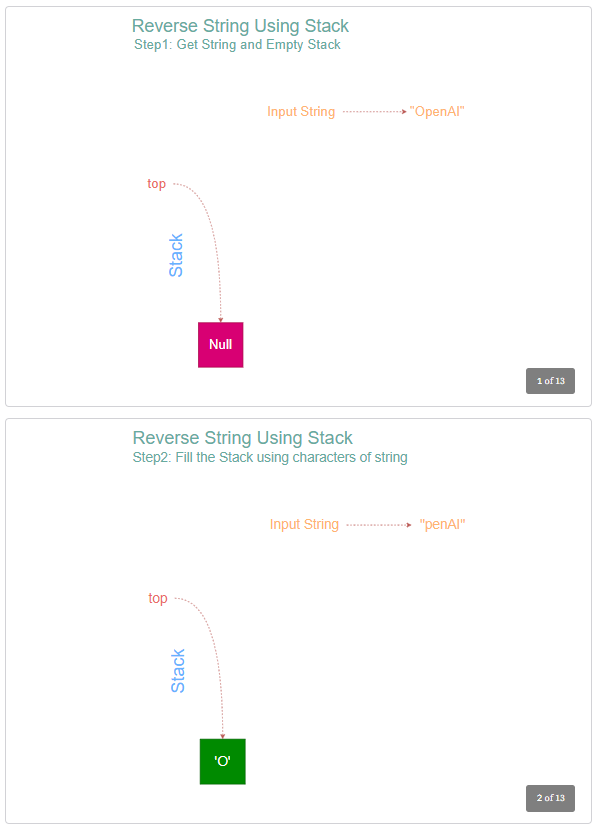
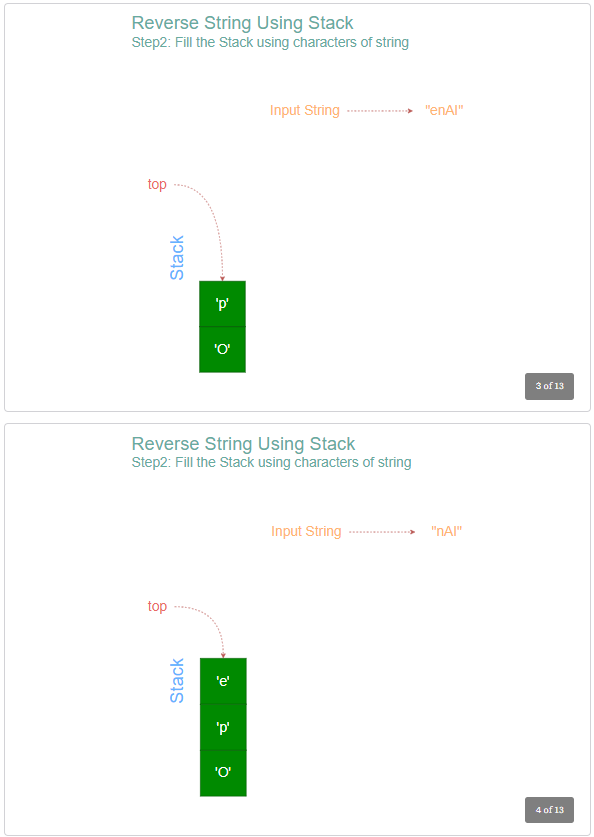
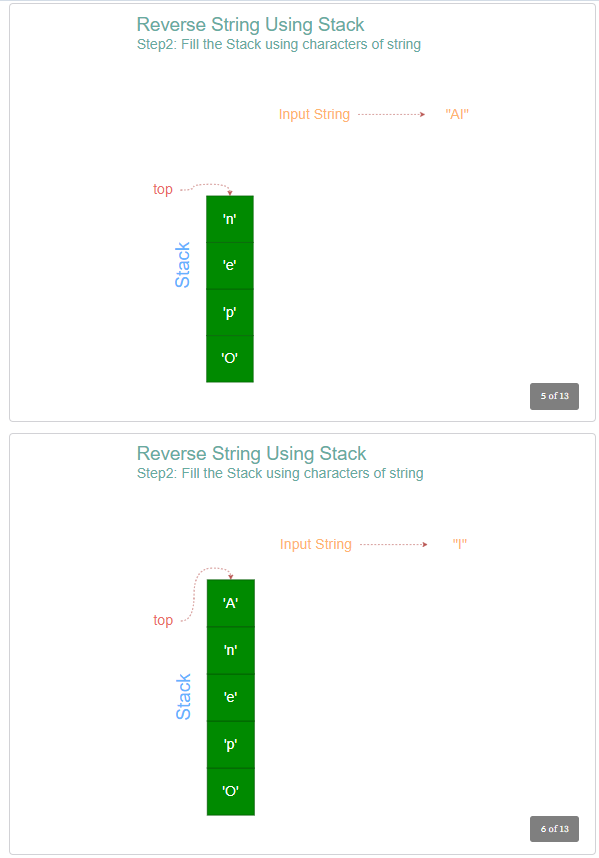
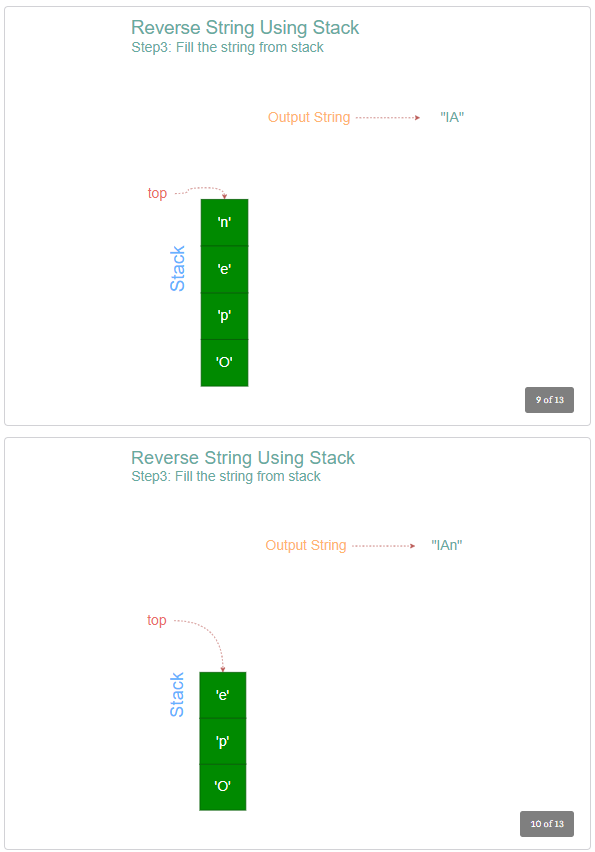
Code

Here is how we can implement this algorithm:

# Define a class named Solution
class Solution:
    # Define a method called reverseString within the class
    def reverseString(self, s):
        # Convert the input string 's' into a list of characters and store it in the 'stack' variable
        # 直接转换的写法可以记一下
        stack = list(s)
        # Initialize an empty string to store the reversed string
        reversed_str = ''
        
        # Use a loop to pop characters from the 'stack' and append them to 'reversed_str'
        # This effectively reverses the order of characters in the string
        while stack:
            reversed_str += stack.pop()
        
        # Return the reversed string
        return reversed_str

# Create an instance of the Solution class
rs = Solution()

# Test the reverseString method with different input strings and print the results
print(rs.reverseString("Hello, World!"))  # Output: "!dlroW ,olleH"
print(rs.reverseString("OpenAI"))  # Output: "IAnepO"
print(rs.reverseString("Stacks are fun!"))  # Output: "!nuf era skcatS"

Time and Space Complexity:

Time Complexity: O(n), where n is the length of the input string. This is because we iterate through the string once to push all characters into the stack and then another time to pop all characters out of the stack.

Space Complexity: O(n), where n is the length of the input string. This is because we use a stack to hold all characters of the string.

Decimal to Binary Conversion

Design Gurus

Problem Statement

Given a positive integer n, write a function that returns its binary equivalent as a string. The function should not use any in-built binary conversion function.

Examples

Example 1:

Input: 2
Output: "10"
Explanation: The binary equivalent of 2 is 10.

Example 2:

Input: 7
Output: "111"
Explanation: The binary equivalent of 7 is 111.

Example 3:

Input: 18
Output: "10010"
Explanation: The binary equivalent of 18 is 10010.

Constraints:

• 0 <= num <= 10^9

Solution

We can use a stack to efficiently create the binary representation of a given decimal number. Our algorithm will take advantage of the ‘Last In, First Out’ property of stacks to reverse the order of the binary digits, since the binary representation is constructed from least significant bit to most significant bit, but needs to be displayed in the opposite order. The procedure involves repeatedly dividing the decimal number by 2, pushing the remainder onto the stack, which corresponds to the binary digit. When the number is reduced to 0, the algorithm pops elements off the stack and appends to the result string until the stack is empty, thereby reversing the order of digits. The result is the binary equivalent of the input decimal number.

Here is a detailed walkthrough of the solution:

1. First, the algorithm starts by creating an empty stack. A stack is chosen because of its “Last In, First Out” property which is perfect for this type of problem where we need to reverse the order of the operations.
2. Then, it enters into a loop where the given number is repeatedly divided by 2. This is because the binary number system is base 2, and each bit represents a power of 2.
3. Inside the loop, the remainder when the number is divided by 2 (which is either 0 or 1) is pushed onto the stack. This remainder is essentially the bit in the binary representation of the number.
4. The number is then updated by integer division by 2 (in programming languages, this is usually denoted by num //= 2 or num = Math.floor(num / 2) or num /= 2). This step essentially “shifts” the number one bit to the right.
5. Steps 3 and 4 are repeated until the number becomes zero.
6. At this point, the stack contains the binary representation of the number, but in reverse order. This is because the first bit we calculated (the least significant bit, or the “rightmost” bit) is on the top of the stack, while the last bit we calculated (the most significant bit, or the “leftmost” bit) is on the bottom of the stack.
7. So, the next step is to reverse this order. This is done by popping the stack until it’s empty and appending each popped bit to the result. Since a stack follows “Last In, First Out” rule, this will correctly reverse the order of the bits.
8. Finally, the algorithm returns the result, which is the binary representation of the original number.

Code

Here is how we can implement this algorithm:

from collections import deque

class Solution:
    def decimalToBinary(self, num):
        stack = deque()  # Create an empty stack to hold binary digits.
        # stack = [] # 原版，但是我比较习惯deque,而且不会对时间和空间复杂度有影响
        while num > 0:  # Continue the loop until num becomes 0.
            stack.appendleft(num % 2)  # Push the remainder of num divided by 2 onto the stack.
            num //= 2  # Update num by integer division (floor division) by 2.
        return ''.join(str(i) for i in stack)  # Convert the stack to a binary string.

# Test cases
sol = Solution()
print(sol.decimalToBinary(2))    # Output: "10" (Binary representation of 2)
print(sol.decimalToBinary(7))    # Output: "111" (Binary representation of 7)
print(sol.decimalToBinary(18))   # Output: "10010" (Binary representation of 18)

Time and Space Complexity Analysis

The time complexity of this algorithm is O(log(n)) due to the division by 2 at each step.

The space complexity is also O(log(n)) because in each step we will be pushing an element on the stack, and there are a total of log(n) steps.

Next Greater Element

Design Gurus

Problem Statement

Given an array, print the Next Greater Element (NGE) for every element.

The Next Greater Element for an element x is the first greater element on the right side of x in the array.

Elements for which no greater element exist, consider the next greater element as -1.

Examples

Example 1:

Input: [4, 5, 2, 25]
Output: [5, 25, 25, -1]
Explanation: The NGE for 4 is 5, 5 is 25, 2 is 25, and there is no NGE for 25.

Example 1:

Input: [13, 7, 6, 12]
Output: [-1, 12, 12, -1]

Example 1:

Input: [1, 2, 3, 4, 5]
Output: [2, 3, 4, 5, -1]

Constraints:

• 1 <= arr.length <= 10^4
• -109 <= arr[i] <= 10^9

Solution:

A simple algorithm is to run two loops: the outer loop picks all elements one by one, and the inner loop looks for the first greater element for the element picked by the outer loop. However, this algorithm has a time complexity of .

We can use a more optimized approach using Stack data structure. The algorithm will leverage the nature of the stack data structure, where the most recently added (pushed) elements are the first ones to be removed (popped). Starting from the end of the array, the algorithm always maintains elements in the stack that are larger than the current element. This way, it ensures that it has a candidate for the “next larger element”. If there is no larger element, it assigns -1 to that position. It handles each element of the array only once, making it an efficient solution.

Detailed Step-by-Step Walkthrough

1. The function receives an array arr.
2. Initialize an empty stack s and an output array res of size equal to the input array, with all elements initialized to -1. res will store the result, i.e., the next larger element for each position in the array.
3. Start a loop that goes from the last index of the array to the first (0 index).
4. In each iteration, while there are elements in the stack and the top element of the stack is less than or equal to the current element in the array, remove elements from the stack. This step ensures that we retain only the elements in the stack that are larger than the current element.
5. After the popping process, if there is still an element left in the stack, it is the next larger element for the current array element. So, assign the top element of the stack to the corresponding position in the res array.
6. Now, push the current array element into the stack. This action considers the current element as a possible “next larger element” for the upcoming elements in the remaining iterations.
7. Repeat steps 4-6 for all the elements of the array.
8. At the end of the loop, res will contain the next larger element for each position in the array. Return this array res.

Algorithm Walkthrough

Let’s consider the input and observe how above algorithm works.

1. Initialize Data Structures:
   • Input Array: [13, 7, 6, 12]
   • Result Array: [0, 0, 0, 0] (Initially set to zeros)
   • Stack: Empty (Will store elements during iteration)
2. Processing Each Element (Reverse Order):
   • The algorithm processes the array from right to left.
3. Last Element (Value 12):
   • Stack is empty, indicating no greater element for 12.
   • Result Array: [0, 0, 0, -1] (Updates the last position to -1)
   • Push element 12 onto the stack.
4. Third Element (Value 6):
   • Stack’s top element is 12, which is greater than 6.
   • Result Array: [0, 0, 12, -1] (Updates the value at the third position to 12)
   • Push element 6 onto the stack.
5. Second Element (Value 7):
   • Stack’s top element is 6, which is less than 7, so it’s popped.
   • Next, the stack’s top element is 12, which is greater than 7.
   • Result Array: [0, 12, 12, -1] (Updates the value at the second position to 12)
   • Push element 7 onto the stack.
6. First Element (Value 13):
   • Stack’s top element is 7, which is less than 13, so it’s popped.
   • Next, stack’s top element is 12, which is also less than 13, so it’s popped.
   • Stack is now empty, indicating no greater element for 13.
   • Result Array: [-1, 12, 12, -1] (Updates the first position to -1)
   • Push element 13 onto the stack.

Here is the visual representation of the algorithm:

Code

Here is the code for this algorithm:

from collections import deque


class Solution:
    def nextLargerElement(self, arr):
        # Initialize an empty stack and a result list with -1 values
        s = deque()
        # stack = [] # 原版，但是我比较习惯deque,而且不会对时间和空间复杂度有影响
        res = [-1] * len(arr)

        # Iterate through the array in reverse order
        for i in range(len(arr) - 1, -1, -1):
            # While the stack is not empty and the top element of the stack is less than or equal to the current element
            while s and s[-1] <= arr[i]:
                s.pop()  # Pop elements from the stack until the condition is met

            if s:
                # If the stack is not empty, set the result for the current element to the top element of the stack
                res[i] = s[-1]
            s.append(arr[i])  # Push the current element onto the stack

        return res


sol = Solution()
print(sol.nextLargerElement([4, 5, 2, 25]))  # Example usage
print(sol.nextLargerElement([13, 7, 6, 12]))  # Example usage
print(sol.nextLargerElement([1, 2, 3, 4, 5]))  # Example usage

# 下面的是看了Monotonic Stack中的“Next Greater Element"之后的想法，后面的那道题目也是找greater的，所以使用的是decreasing stack，小的元素在栈顶。这道题官方的解法是从后往前遍历，而后一道题使用的是从后往前遍历+hashmap辅助记住对应关系。经过实验可以发现，这道题也可以使用从后往前遍历+hashmap的方式来进行求解。不过后面Pattern的那道题也说明了从前往后遍历也有可能需要hashmap，这道题从前往后遍历不需要hashmap是特例，因为这里只有一个数组，而后面那道题有两个数组，如果不用hashmap,就要用arr.index方法，也比较复杂。
# 总结来说就是一般从前往后和从后往前都可以，但是应该是都需要一个结构（一般是一个map）来记录对应关系的，这道题的res就是起到了这个作用。**但是一般来说都是从前往后遍历（下一个Pattern 单调栈）**。
# 从前往后遍历，需要一个hashmap来记录对应关系
from collections import deque


class Solution:
    def nextLargerElement(self, arr):
        # Initialize an empty stack and a result list with -1 values
        s = deque()
        res = [-1] * len(arr)
        hashmap = {}

        # Iterate through the array in reverse order
        for i in range(0, len(arr)):
            # While the stack is not empty and the top element of the stack is less than or equal to the current element
            # 因为找的是greater所以这里的判断应该就是s[-1] < arr[i]而不是s[-1] <= arr[i]
            while s and s[-1] < arr[i]:
                top = s.pop()  # Pop elements from the stack until the condition is met
                hashmap[top] = arr[i]
            s.append(arr[i])
        for i in range(len(arr)):
            if arr[i] in hashmap:
                res[i] = hashmap[arr[i]]

        return res
    	# 上面四行可以用下面这一行代替
    	# return [hashmap.get(num, -1) for num in nums1]


sol = Solution()
print(sol.nextLargerElement([4, 5, 2, 25]))  # Example usage
print(sol.nextLargerElement([13, 7, 6, 12]))  # Example usage
print(sol.nextLargerElement([1, 2, 3, 4, 5]))  # Example usage

Time and Space Complexity

Time Complexity: The worst-case time complexity of this algorithm is O(n) as every element is pushed and popped from the stack exactly once.

Space Complexity: The space complexity of this algorithm is O(n) as we are using a stack and an array to store the next greater elements.

Sorting a Stack

Design Gurus

Problem Statement

Given a stack, sort it using only stack operations (push and pop).

You can use an additional temporary stack, but you may not copy the elements into any other data structure (such as an array). The values in the stack are to be sorted in descending order, with the largest elements on top.

Examples

1. Input: [34, 3, 31, 98, 92, 23]
   Output: [3, 23, 31, 34, 92, 98]

2. Input: [4, 3, 2, 10, 12, 1, 5, 6]
   Output: [1, 2, 3, 4, 5, 6, 10, 12]

3. Input: [20, 10, -5, -1]
   Output: [-5, -1, 10, 20]

Solution

This problem can be solved by using a temporary stack as auxiliary storage. The algorithm takes an input stack and sorts it using a temporary stack tmpStack. The sorting process is done by continuously popping elements from the input stack and pushing them onto the tmpStack in sorted order, rearranging elements as necessary between the stacks until the original stack is empty.

This algorithm leverages the LIFO (last in, first out) nature of a stack. It removes elements from the original stack one by one and uses a second stack to keep the elements sorted. If the top element of the sorted stack is larger than the current element, it moves the larger elements back to the original stack until it finds the correct spot for the current element, at which point it pushes the current element onto the sorted stack. Because of this, the smaller elements end up at the bottom of the sorted stack and the largest element on the top, resulting in a stack sorted in descending order from top to bottom.

Detailed Step-by-Step Walkthrough

1. The sort method receives an input stack.
2. It initializes an empty temporary stack tmpStack.
3. The algorithm enters a loop that continues until the input stack is empty.
4. In each iteration, it pops the top element (tmp) from the input stack.
5. Then it enters another loop, which continues as long as tmpStack is not empty and the top of tmpStack is larger than tmp. In each iteration of this inner loop, it pops the top element from tmpStack and pushes it back onto the input stack.
6. After the inner loop ends, it pushes tmp onto tmpStack. The inner loop ensures that tmpStack is always sorted in descending order, with smaller elements at the bottom and larger elements at the top, and tmp is placed into its correct position in this order.
7. Once the outer loop ends and the input stack is empty, tmpStack contains all the elements originally in the input stack but sorted in descending order.
8. It then returns tmpStack.

Algorithm Walkthrough

1. Initial Setup:

   • Input Stack (top to bottom): [34, 3, 31, 98, 92, 23]
   • Temporary Stack (tmpStack): Empty

2. Process Element: 23

   • Pop 23 from the input stack.
   • tmpStack is empty, so push 23 onto tmpStack.
   • Input Stack: [34, 3, 31, 98, 92], tmpStack: [23]

3. Process Element: 92

   • Pop 92 from the input stack.
   • Since 23 < 92, push 92 onto tmpStack.
   • Input Stack: [34, 3, 31, 98], tmpStack: [23, 92]

4. Process Element: 98

   • Pop 98 from the input stack.
   • Since 92 < 98, push 98 onto tmpStack.
   • Input Stack: [34, 3, 31], tmpStack: [23, 92, 98]

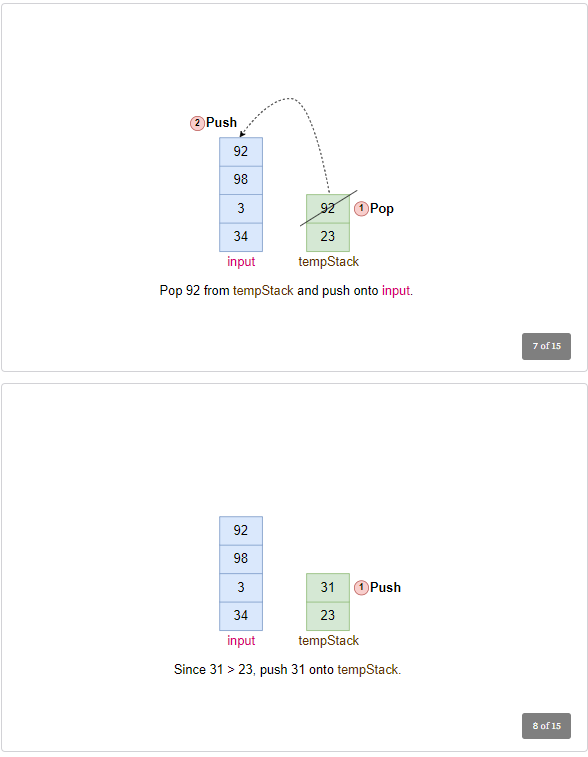
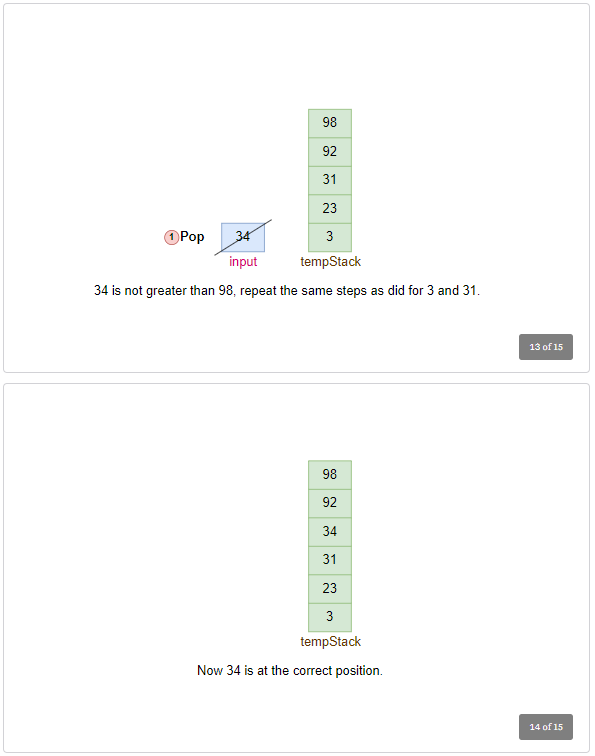
5. Process Element: 31

   • Pop 31 from the input stack.
   • Move elements from tmpStack to input stack until the correct position for 31 is found.
   • Pop 98, then 92 from tmpStack and push them onto the input stack.
   • Push 31 onto tmpStack.
   • Input Stack: [34, 3, 98, 92], tmpStack: [23, 31]
   • In next 2 iterations, pop 98, and 92 from input stack and push back to the tmpStack. Updated stack will be: Input Stack: [34, 3], tmpStack: [23, 31, 92, 98].

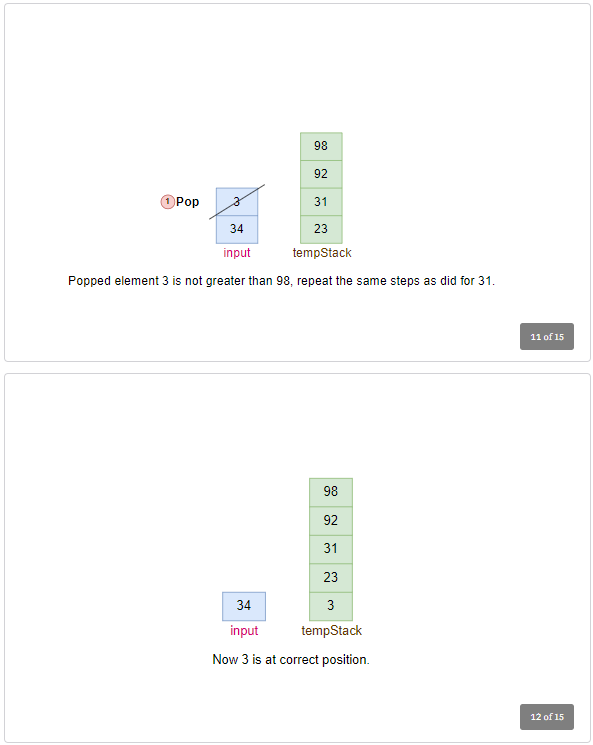
6. Process Element: 3

   • Pop 3 from the input stack.

• Move elements from tmpStack to input stack until the correct position for 3 is found.
  • Pop 98, 92, 31, then 23 from tmpStack and push them onto the input stack.
• Push 3 onto tmpStack.
  • Input Stack: [34, 98, 92, 31, 23], tmpStack: [3]
    • In next 4 iterations, pop 98, 92, 31, and 23 from the input stack and push back to the tmpStack. Updated stack will be: Input Stack: [34], tmpStack: [3, 23, 31, 92, 98].

1. Process Element: 34

   • Pop 34 from the input stack.
   • Move elements from tmpStack to input stack until the correct position for 34 is found.
   • Pop 98, then 92 from tmpStack and push them onto the input stack.
   • Push 34 onto tmpStack.
   • Input Stack: [98, 92], tmpStack: [3, 23, 31, 34].
   • In next 2 iterations, pop 98, and 92 from the input stack and push to the tmpStack.

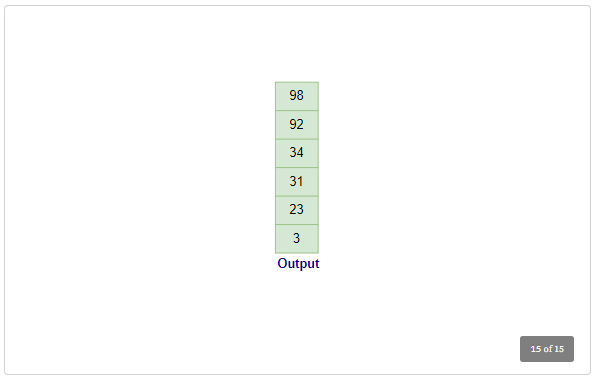
2. Final Result:

   • Input Stack: Empty
   • tmpStack (Sorted, top to bottom): [3, 23, 31, 34, 92, 98]

Here is the visual representation of the algorithm:

Code

Here is the code for this algorithm:

from collections import deque


class Solution:
    def sortStack(self, stack):
        # Create an empty stack to store the sorted elements
        tempStack = deque()
        # tempStack = [] # 原版，但是我比较习惯deque,而且不会对时间和空间复杂度有影响
        
        # Continue sorting until the original stack is empty
        while stack:
            # Pop the top element from the original stack
            temp = stack.pop()
            
            # Move elements from the temporary stack back to the original stack
            # until we find the correct position for the current element
            while tempStack and tempStack[-1] > temp:
                stack.append(tempStack.pop())
            
            # Place the current element in its correct sorted position in the temporary stack
            tempStack.append(temp)
        
        # Return the sorted stack
        # return tempStack # 原版
        return list(tempStack) # 配合deque


# Example usage
sol = Solution();
stack = [34, 3, 31, 98, 92, 23]
print("Input: ", stack)
print("Sorted Output: ", sol.sortStack(stack))

Time and Space Complexity

Time Complexity

The time complexity of the sort stack algorithm is O(n\^2) , where n is the number of elements in the stack. This is because, in the worst case, for every element that we pop from the input stack, we might have to pop all the elements in the temporary stack (and push them back to the original stack) to find the correct place to insert the element. Since we have to do this for all n elements, the time complexity is n n = n^2*.

Space Complexity

The space complexity of the algorithm is O(n). This is because we use an additional temporary stack to sort the elements. In the worst-case scenario, this temporary stack could store all the elements of the original stack. Thus, the space complexity is directly proportional to the number of elements in the input stack, making it linear, O(n).

Please note that the space complexity does not count the input size itself (the input stack in this case), it only counts the extra space we use related to the size of the input. If we were to count the input size as well, the total space used would be O(2n), but since we drop the constant factor when expressing space complexity, so it remains O(n).

Simplify Path

Top Interview 150 | 71. Simplify Path Design Gurus

Problem Statement

Given an absolute file path in a Unix-style file system, simplify it by converting “..” to the previous directory and removing any “.” or multiple slashes. The resulting string should represent the shortest absolute path.

Examples:

1. 
   Input: "/a//b////c/d//././/.."
   Output: "/a/b/c"
   
2. 
   Input: "/../"
   Output: "/"

3. 
   Input: "/home//foo/"
   Output: "/home/foo"

Constraints:

• 1 <= path.length <= 3000
• path consists of English letters, digits, period ‘.’, slash ‘/‘ or ‘_’.
• path is a valid absolute Unix path.

Solution

To simplify the path, we’ll use a stack to track the directories we’re currently in. We’ll split the input path into components by the “/“ character, then process each component one by one. If a component is “..”, we go to the previous directory by popping the top of the stack. If a component is “.” or an empty string, we do nothing. Otherwise, we push the component into the stack as a new directory.

Detailed Algorithm steps:

1. Split the input path by the “/“ character into an array of components.
2. Initialize an empty stack.
3. For each component in the array:
   • If the component is “..”, pop the top of the stack (if it’s not already empty).
   • Else if the component is “.” or an empty string, do nothing.
   • Else, push the component into the stack as a new directory.
4. Finally, combine the components in the stack into a string, separated by the “/“ character. Add a “/“ at the start to denote an absolute path.

Algorithm walkthrough

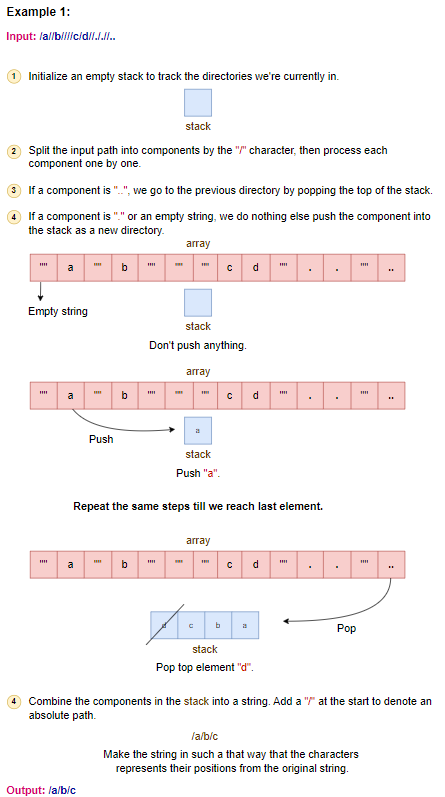
let’s walk through the code using the input "/a//b////c/d//././/.." step by step:

1. Initialize a Stack: A Stack<String> is created to store components of the simplified path.

2. Split the Path: The input path "/a//b////c/d//././/.." is split using "/" as the delimiter. The resulting parts are: ["", "a", "", "b", "", "", "", "c", "d", "", ".", "", ".", "", "", ".."]. Empty strings and dots (".") represent the current directory and will be ignored in further processing.

3. Process Each Part:

   • First Part (""): It’s empty, so it’s ignored.
   • Second Part ("a"): It’s a directory name and is pushed onto the stack.
   • Third Part (""): Ignored.
   • Fourth Part ("b"): Another directory name, pushed onto the stack.
   • Next Several Parts ("", "", ""): All empty, so ignored.
   • Part "c": A directory name, pushed onto the stack.
   • Part "d": Another directory name, pushed onto the stack.
   • Part ".": Represents the current directory, ignored.
   • Part "." (again): Again, represents the current directory, ignored.
   • Last Part (".."): Represents moving up one directory. It pops "d" from the stack.

   After processing, the stack contains: ["a", "b", "c"].

4. Reconstruct Simplified Path:

   • A StringBuilder is used to construct the final simplified path.
   • The stack is processed in LIFO (Last-In-First-Out) order. Each component is popped and appended to the start of the result string, preceded by "/".
   • After processing the stack, the StringBuilder contains "/a/b/c".

5. Return the Result:

   • The StringBuilder is converted to a string and returned.
   • For the given input, the output is "/a/b/c".

Here is the visual representation of the algorithm:

Code

Here is the code for this algorithm:

from collections import deque


class Solution:
    def simplifyPath(self, path):
        # Create a stack to store the simplified path components
        stack = deque()
        # stack = [] # 原版，但是我比较习惯deque,而且不会对时间和空间复杂度有影响

        # Split the input path string using '/' as a delimiter
        for p in path.split('/'):
            if p == '..':
                # If the component is '..', pop the last component from the stack
                if stack:
                    stack.pop()
            elif p and p != '.':
                # If the component is not empty and not '.', push it onto the stack
                stack.append(p)

        # Reconstruct the simplified path by joining components from the stack
        return '/' + '/'.join(stack)


# Test cases
sol = Solution();
print(sol.simplifyPath("/a//b////c/d//././/.."))  # Expected output: "/a/b/c"
print(sol.simplifyPath("/../"))  # Expected output: "/"
print(sol.simplifyPath("/home//foo/"))  # Expected output: "/home/foo"

Time and Space Complexity

The time complexity of the algorithm is O(n), where n is the size of the input path, since we process each character once. The space complexity is also O(n), as we store each directory in a stack.

Author：Hasuer

Link：https://hasuer.github.io/7-pattern-stack/index.html

Publish date：May 7th 2024, 5:16:48 pm

Update date：May 28th 2024, 11:27:52 am

License：本文采用知识共享署名-非商业性使用 4.0 国际许可协议进行许可

• Next Post
  8. Pattern Monotonic Stack
• Previous Post
  6. Pattern In-place Reversal of a LinkedList

Powered by Hexotheme Archer

PV: :)

CATALOG

1. 1. Introduction to Stack
   1. 1.1. Real-world Examples of Stacks
   2. 1.2. The LIFO Principle
2. 2. Operations on Stack
   1. 2.1. Push Operation
   2. 2.2. Pop Operation
   3. 2.3. Peek or Top Operation
   4. 2.4. IsEmpty Operation
   5. 2.5. Putting it All Together
   6. 2.6. Dealing with Stack Overflow and Underflow
3. 3. Implementing Stack Data Structure
   1. 3.1. Stack Implementation Using an Array
   2. 3.2. Stack Implementation Using Linked List
   3. 3.3. Memory Management
   4. 3.4. Expression Evaluation and Syntax Parsing
   5. 3.5. Undo Mechanism in Software Applications
   6. 3.6. Backtracking Algorithms
   7. 3.7. Depth-First Search (DFS)
   8. 3.8. Web Page History in Browsers
   9. 3.9. Conclusion
4. 4. Balanced Parentheses
   1. 4.1. Problem Statement
   2. 4.2. Solution
      1. 4.2.1. Algorithm Walkthrough
   3. 4.3. Code
   4. 4.4. Time and Space Complexity Analysis
5. 5. Reverse a String
   1. 5.1. Problem Statement
      1. 5.1.1. Examples
   2. 5.2. Solution
   3. 5.3. Code
   4. 5.4. Time and Space Complexity:
6. 6. Decimal to Binary Conversion
   1. 6.1. Problem Statement
      1. 6.1.1. Examples
   2. 6.2. Solution
   3. 6.3. Code
   4. 6.4. Time and Space Complexity Analysis
7. 7. Next Greater Element
   1. 7.1. Problem Statement
      1. 7.1.1. Examples
   2. 7.2. Solution:
      1. 7.2.1. Algorithm Walkthrough
   3. 7.3. Code
   4. 7.4. Time and Space Complexity
8. 8. Sorting a Stack
   1. 8.1. Problem Statement
      1. 8.1.1. Examples
   2. 8.2. Solution
      1. 8.2.1. Algorithm Walkthrough
   3. 8.3. Code
   4. 8.4. Time and Space Complexity
9. 9. Simplify Path
   1. 9.1. Problem Statement
      1. 9.1.1. Examples:
   2. 9.2. Solution
      1. 9.2.1. Algorithm walkthrough
   3. 9.3. Code
   4. 9.4. Time and Space Complexity

• Archive
• Tag
• Cate

Total : 41

2024

• 06/02 34. Conclusions
• 06/02 33. Test Your Knowledge (Hard)
• 06/01 32. Test Your Knowledge (Medium)
• 05/31 31. Test Your Knowledge (Easy).md
• 05/30 30. Revision
• 05/29 29. Miscellaneous
• 05/28 28. Pattern Multi-thread
• 05/27 27. Pattern Prefix Sum
• 05/26 26. Pattern Ordered Set
• 05/25 25. Pattern Union Find
• 05/24 24. Pattern Topological Sort (Graph)
• 05/23 23. Pattern Trie
• 05/22 22. Pattern Backtracking
• 05/21 21. Pattern 01 Knapsack (Dynamic Programming)
• 05/20 20. Pattern Greedy Algorithms
• 05/19 19. Pattern K-way merge
• 05/18 18. Pattern Top 'K' Elements
• 05/17 17. Pattern Bitwise XOR
• 05/16 16. Pattern Modified Binary Search
• 05/15 15. Pattern Subsets
• 05/14 14. Pattern Two Heaps
• 05/13 13. Pattern Island (Matrix traversal)
• 05/12 12. Pattern Graphs
• 05/11 11. Pattern Tree Depth First Search
• 05/10 10. Pattern Tree Breadth First Search
• 05/09 9. Pattern Hash Maps
• 05/08 8. Pattern Monotonic Stack
• 05/07 7. Pattern Stack
• 05/06 6. Pattern In-place Reversal of a LinkedList
• 05/05 5. Pattern Cyclic Sort
• 05/04 4. Pattern Merge Intervals
• 05/03 3. Pattern Sliding Window
• 05/02 2. Pattern Fast_Slow pointers
• 05/01 1. Pattern Two Pointers
• 04/30 0.Introduction

2022

• 06/12 Ubuntu20.04安装配置MySQL8(详细)
• 02/25 Axios学习笔记
• 02/23 Promise学习笔记
• 02/23 Nginx学习笔记
• 02/23 AJAX学习笔记

2021

• 07/07 Git学习笔记

 Interview



缺失模块，请参考主题文档进行安装配置：https://github.com/fi3ework/hexo-theme-archer#%E5%AE%89%E8%A3%85%E4%B8%BB%E9%A2%98

 技术笔记  Grokking-Interview-Pattern

