Hasuer's Studio.

27. Pattern Prefix Sum

Grokking Interview Pattern Interview
Word count: 7.2kReading time: 44 min
2024/05/27

416. Partition Equal Subset Sum Design Gurus Educative.io

ATTENTION: 这些题目还没有看

Introduction Prefix Sum Pattern

What is Prefix Sum?

A prefix sum is the cumulative sum of elements in an array up to a certain index. It is a powerful tool for efficiently solving range sum queries and various subarray problems. By precomputing the prefix sums of an array, we can quickly calculate the sum of any subarray in constant time. This technique is widely used in algorithmic problems to improve performance and reduce time complexity, making it essential for handling large datasets and multiple queries efficiently.

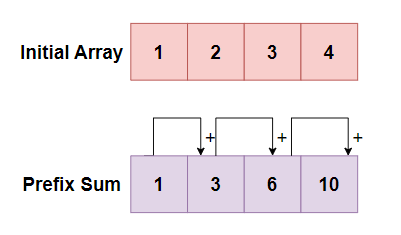
For example, if we have an array ([1, 2, 3, 4]), the prefix sums would be calculated as follows:

  • Prefix sum at index 0: (1)
  • Prefix sum at index 1: (1 + 2 = 3)
  • Prefix sum at index 2: (1 + 2 + 3 = 6)
  • Prefix sum at index 3: (1 + 2 + 3 + 4 = 10)

So, the prefix sum array for ([1, 2, 3, 4]) is ([1, 3, 6, 10]).

Algorithm to Calculate Prefix Sum

  1. Initialize an array prefix of the same length as the input array.
  2. Set prefix[0] to arr[0].
  3. For each subsequent element, set prefix[i] to prefix[i-1] + arr[i].
  4. Return the prefix array.

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution:
    def compute_prefix_sum(self, arr):
        # Initialize the prefix array with zeros
        prefix = [0] * len(arr)

        # Set the first element of the prefix array to the first element of the input array
        prefix[0] = arr[0]

        # Compute the prefix sum for each subsequent element
        for i in range(1, len(arr)):
            prefix[i] = prefix[i - 1] + arr[i]

        # Return the computed prefix sum array
        return prefix


if __name__ == "__main__":
    sol = Solution()
    arr = [1, 2, 3, 4]
    prefix_sum = sol.compute_prefix_sum(arr)
    print(prefix_sum)  # Output: [1, 3, 6, 10]

Complexity Analysis

Time Complexity
  • Computation: The for-loop runs (n-1) times, where (n) is the length of the input array, resulting in O(n) time.

Therefore, the overall time complexity is O(n).

Space Complexity
  • Prefix Array: The prefix array requires O(n) space, where (n) is the length of the input array.
  • Input Array: The input array itself requires O(n) space.

Thus, the overall space complexity is O(n).

Why Use Prefix Sums?

Prefix sums are used to improve the efficiency of range sum queries. Without a prefix sum, calculating the sum of elements between two indices (i) and (j) in an array requires iterating through the elements from (i) to (j), which takes O(n) time. By precomputing the prefix sums, we can answer these queries in O(1) time.

Example: Range Sum Query

Given an array nums and a range query (i, j), find the sum of elements between indices i and j.

Example
  • Input: arr = [1, 2, 3, 4], i = 1, j = 3
  • Output: 9
  • Justification: The sum of 2, 3 and 4 is 9.
Step-by-Step Algorithm
  1. Compute the Prefix Sum Array:
    • Initialize a prefix array prefix of the same length as the input array.
    • Set prefix[0] to the first element of the input array.
    • Iterate through the input array starting from index 1:
      • Set prefix[i] to prefix[i-1] + arr[i].
    • The prefix sum array is now ready to be used for range sum queries.
  2. Answer the Range Sum Query:
    • For a given range ([i, j]):
      • If (i = 0), the sum is prefix[j].
      • Otherwise, the sum is prefix[j] - prefix[i-1].
Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution:
    def compute_prefix_sum(self, arr):
        # Step 1: Initialize the prefix array with zeros
        prefix = [0] * len(arr)
        
        # Step 2: Set the first element of the prefix array to the first element of the input array
        prefix[0] = arr[0]
        
        # Step 3: Compute the prefix sum for each subsequent element
        for i in range(1, len(arr)):
            prefix[i] = prefix[i - 1] + arr[i]
        
        # Step 4: Return the computed prefix sum array
        return prefix

    def range_sum_query(self, prefix, i, j):
        # Step 5: Calculate the sum of elements between indices i and j using the prefix array
        if i == 0:
            return prefix[j]
        return prefix[j] - prefix[i - 1]

if __name__ == "__main__":
    sol = Solution()
    arr = [1, 2, 3, 4]
    prefix_sum = sol.compute_prefix_sum(arr)
    range_sum = sol.range_sum_query(prefix_sum, 1, 3)
    print("Sum of elements from index 1 to 3:", range_sum)  # Output: 9

Complexity Analysis

Time Complexity:

  • Computation: The for-loop runs (n-1) times, resulting in O(n) time.
  • Range Sum Query: Answering a range sum query takes O(1) time.

Therefore, the overall time complexity is O(n) for preprocessing and O(1) for each query.

Space Complexity:

  • Prefix Array: The prefix array requires O(n) space.
  • Input Array: The input array itself requires O(n) space.

Thus, the overall space complexity is O(n).

Applications of Prefix Sums

  1. Range Sum Queries: As explained above, prefix sums can quickly answer the sum of elements between any two indices in an array.
  2. Subarray Problems: Prefix sums are used to find subarrays with a given sum, maximum sum subarray, and other subarray-related problems.
  3. 2D Prefix Sums: Extending the concept to two-dimensional arrays helps in efficiently calculating the sum of elements in sub-matrices.
  4. Frequency Counting: Prefix sums can be used to maintain cumulative frequencies, helping in statistical calculations and data analysis.
  5. Balancing Loads: In distributed systems, prefix sums can help in balancing workloads evenly across multiple servers.

By understanding and utilizing prefix sums, you can solve many algorithmic problems more efficiently, making your solutions both faster and more elegant.

Find the Middle Index in Array

Problem Statement

Given an integer array nums, return the leftmost middleIndex (i.e., the smallest amongst all the possible ones).

A middleIndex is an index where the sum of the numbers to the left of this index is equal to the sum of the numbers to the right of this index.

You can consider the left sum 0 for middleIndex == 0, and right sum 0 for middleIndex == nums.length - 1.

If no middleIndex exists in nums, return -1.

Examples

Example 1:

  • Input: nums = [1, 7, 3, 6, 5, 6]
  • Expected Output: 3
  • Justification: The sum of the numbers to the left of index 3 (1 + 7 + 3 = 11) is equal to the sum of the numbers to the right of index 3 (5 + 6 = 11).

Example 2:

  • Input: nums = [2, 1, -1]
  • Expected Output: 0
  • Justification: The sum of the numbers to the left of index 0 is considered to be 0. The sum of the numbers to the right of index 0 (1 + -1 = 0) is also 0.

Example 3:

  • Input: nums = [2, 3, 5, 5, 3, 2]
  • Expected Output: -1
  • Justification: There is no middleIndex exists in the array.

Constraints:

  • 1 <= nums.length <= 100
  • -1000 <= nums[i] <= 1000

Solution

To solve this problem, we need to find an index where the sum of the elements on the left equals the sum of the elements on the right. We can achieve this by calculating the total sum of the array first. Then, as we iterate through the array, we keep a running sum of the elements to the left of the current index. By subtracting this running sum and the current element from the total sum, we get the sum of the elements to the right of the current index. If the left sum equals the right sum at any index, we return that index. This approach ensures that we only need to traverse the array once, making it efficient in terms of time complexity.

This method is effective because it minimizes the number of passes over the array, reducing the overall time complexity to O(n). Additionally, it only requires a few extra variables for storing sums, keeping the space complexity to O(1). This combination of efficiency and simplicity makes it a robust solution for finding the middle index.

Step-by-step Algorithm

  • Calculate the total sum of the array.
  • Initialize a variable leftSum to 0.
  • Iterate through the array using a loop:
    • For each element at index i, calculate the right sum as totalSum - leftSum - nums[i].
    • If leftSum equals the right sum, return i.
    • Update leftSum by adding the current element nums[i].
  • If no index is found, return -1.

Algorithm Walkthrough

Let’s walk through the algorithm using the example nums = [1, 7, 3, 6, 5, 6].

  • Step 1: Calculate totalSum = 1 + 7 + 3 + 6 + 5 + 6 = 28.

  • Step 2: Initialize leftSum = 0.

  • Step 3

    : Start loop through the array.

    • Index 0: rightSum = 28 - 0 - 1 = 27. leftSum = 0 + 1 = 1.
    • Index 1: rightSum = 28 - 1 - 7 = 20. leftSum = 1 + 7 = 8.
    • Index 2: rightSum = 28 - 8 - 3 = 17. leftSum = 8 + 3 = 11.
    • Index 3: rightSum = 28 - 11 - 6 = 11.
      • leftSum equals rightSum at index 3. Return 3.

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution:
    def findMiddleIndex(self, nums) -> int:
        # Calculate the total sum of all elements in the array
        totalSum = sum(nums)
        # Initialize the sum of elements to the left
        leftSum = 0
        # Iterate through each element in the array
        for i, num in enumerate(nums):
            # Calculate the sum of elements to the right
            rightSum = totalSum - leftSum - num
            # Check if the sum of elements to the left equals the sum of elements to the right
            if leftSum == rightSum:
                return i
            # Update the sum of elements to the left
            leftSum += num
        return -1

solution = Solution()
example1 = [1, 7, 3, 6, 5, 6]
example2 = [2, 1, -1]
example3 = [2, 3, 5, 5, 3, 2]
print(solution.findMiddleIndex(example1))  # Output: 3
print(solution.findMiddleIndex(example2))  # Output: 0
print(solution.findMiddleIndex(example3))  # Output: -1

Complexity Analysis

Time Complexity: O(N)

  • We traverse the array twice, once to calculate the total sum and once to find the middle index.

Space Complexity: O(1)

  • We use a constant amount of extra space for variables (totalSum, leftSum).

Left and Right Sum Differences (easy)

Problem Statement

Given an input array of integers nums, find an integer array, let’s call it differenceArray, of the same length as an input integer array.

Each element of differenceArray, i.e., differenceArray[i], should be calculated as follows: take the sum of all elements to the left of index i in array nums (denoted as leftSum[i]), and subtract it from the sum of all elements to the right of index i in array nums (denoted as rightSum[i]), taking the absolute value of the result. Formally:

differenceArray[i] = | leftSum[i] - rightSum[i] |

If there are no elements to the left/right of i, the corresponding sum should be taken as 0.

Examples

Example 1:

  • Input: [2, 5, 1, 6]
  • Expected Output: [12, 5, 1, 8]
  • Explanation:
    • For i=0: |(0) - (5+1+6)| = |0 - 12| = 12
    • For i=1: |(2) - (1+6)| = |2 - 7| = 5
    • For i=2: |(2+5) - (6)| = |7 - 6| = 1
    • For i=3: |(2+5+1) - (0)| = |8 - 0| = 8

Example 2:

  • Input: [3, 3, 3]
  • Expected Output: [6, 0, 6]
  • Explanation:
    • For i=0: |(0) - (3+3)| = 6
    • For i=1: |(3) - (3)| = 0
    • For i=2: |(3+3) - (0)| = 6

Example 3:

  • Input: [1, 2, 3, 4, 5]
  • Expected Output: [14, 11, 6, 1, 10]
  • Explanation:
    • Calculations for each index i will follow the above-mentioned logic.

Constraints:

  • 1 <= nums.length <= 1000
  • 1 <= nums[i] <= 105

Solution

The algorithm takes a numerical approach to find the absolute differences between the sum of numbers to the left and to the right of each index in the input array, nums. It efficiently calculates two new arrays: leftSum and rightSum that respectively store the cumulative sums of elements to the left and right of every index i (inclusive). Afterward, it calculates the absolute difference between corresponding values in leftSum and rightSum to form the resulting array, differenceArray. This algorithm ensures minimized repeated calculations, as each sum is calculated in a linear pass and reused while determining the absolute differences.

  1. Initialize Arrays:
    • A new array, leftSum, is initialized with the same length as nums to keep track of the cumulative sum to the left of each index.
    • Similarly, rightSum is initialized to keep track of the cumulative sum to the right of each index.
    • differenceArray is initialized to store the final results.
  2. Populate the leftSum Array:
    • Traverse nums from left to right.
    • For each index i, leftSum[i] is determined by adding nums[i] to leftSum[i-1]. If i is 0, leftSum[i] is simply nums[i] since there are no elements to the left.
  3. Populate the rightSum Array:
    • Traverse nums from right to left.
    • For each index i, rightSum[i] is determined by adding nums[i] to rightSum[i+1]. If i is the last index, rightSum[i] is nums[i] since there are no elements to the right.
  4. Calculate the differenceArray:
    • Traverse from index 0 to length-1 of nums.
    • For each i, differenceArray[i] is calculated as the absolute difference between leftSum[i] and rightSum[i].
  5. Return the Result:
    • differenceArray is returned as it contains the final result.

Algorithm Walkthrough

Consider the example where nums = [2, 5, 1, 6] for a detailed walkthrough.

  • Step 1: Initialize Arrays:
    • leftSum = [0, 0, 0, 0]
    • rightSum = [0, 0, 0, 0]
    • differenceArray = [0, 0, 0, 0]
  • Step 2: Populate the leftSum Array:
    • i=0: leftSum[0] = nums[0] = 2
    • i=1: leftSum[1] = nums[1] + leftSum[0] = 5 + 2 = 7
    • i=2: leftSum[2] = nums[2] + leftSum[1] = 1 + 7 = 8
    • i=3: leftSum[3] = nums[3] + leftSum[2] = 6 + 8 = 14
  • Step 3: Populate the rightSum Array:
    • i=3: rightSum[3] = nums[3] = 6
    • i=2: rightSum[2] = nums[2] + rightSum[3] = 1 + 6 = 7
    • i=1: rightSum[1] = nums[1] + rightSum[2] = 5 + 7 = 12
    • i=0: rightSum[0] = nums[0] + rightSum[1] = 2 + 12 = 14
  • Step 4: Calculate the differenceArray:
    • differenceArray[i] = |leftSum[i] - rightSum[i]| for each i
    • differenceArray[0] = |2 - 14| = 12
    • differenceArray[1] = |7 - 12| = 5
    • differenceArray[2] = |8 - 7| = 1
    • differenceArray[3] = |14 - 6| = 8
  • Step 5: Return the Result:
    • The final array differenceArray = [12, 5, 1, 8] is returned as the output.

Code

Here is the code for this algorithm:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
class Solution:
    def findDifferenceArray(self, nums):
        n = len(nums)
        leftSum = [0] * n
        rightSum = [0] * n
        differenceArray = [0] * n
        
        # Calculate leftSum array
        leftSum[0] = nums[0]
        for i in range(1, n):
            leftSum[i] = leftSum[i-1] + nums[i]
        
        # Calculate rightSum array
        rightSum[n-1] = nums[n-1]
        for i in range(n-2, -1, -1):
            rightSum[i] = rightSum[i+1] + nums[i]
        
        # Calculate differenceArray
        for i in range(n):
            differenceArray[i] = abs(leftSum[i] - rightSum[i])
        
        return differenceArray

if __name__ == "__main__":
    solution = Solution()
    example1 = [2, 5, 1, 6]
    example2 = [3, 1, 4, 2, 2]
    example3 = [1, 2, 3, 4, 5]
    
    # Output should be: [12, 5, 1, 8]
    print(solution.findDifferenceArray(example1))
    # Output should be: [9, 5, 0, 6, 10]
    print(solution.findDifferenceArray(example2))
    # Output should be: [14, 11, 6, 1, 10]
    print(solution.findDifferenceArray(example3))

Time Complexity

  1. Calculating Prefix and Suffix Sums:

    • Prefix Sum Calculation: The loop that calculates the prefix sum runs n times, where n is the number of elements in the input array. Therefore, it has a time complexity of (O(n)).
    • Suffix Sum Calculation: Similarly, the loop for calculating the suffix sum also runs n times, resulting in a time complexity of (O(n)).

  2. Calculating Answer Array:

    • The loop that calculates the absolute difference between prefix and suffix sums at each index also runs n times, contributing (O(n)) to the time complexity.

    Combining all these, the overall time complexity of the algorithm is (O(n) + O(n) + O(n) = O(3n)), which simplifies to (O(n)) because we typically ignore constant factors in Big O notation.

Space Complexity

  1. Prefix and Suffix Sum Arrays:

    • The algorithm utilizes two additional arrays: prefixSum and suffixSum, each of size n. This contributes (2n) to the space complexity, i.e., (O(2n)).

  2. Answer Array:

    • Additionally, an answer array of size n is used to store the final results. This adds an additional (O(n)) to the space complexity.

    Combining these, the overall space complexity is (O(2n) + O(n) = O(3n)), which simplifies to (O(n)) when considering Big O notation.

Maximum Size Subarray Sum Equals k

Problem Statement

Given an array of integers nums and an integer k, find the length of the longest subarray that sums to k. If no such subarray exists, return 0.

Examples

Example 1:

  • Input: nums = [1, 2, 3, -2, 5], k = 5
  • Output: 2
  • Explanation: The longest subarray with a sum of 5 is [2, 3], which has a length of 2.

Example 2:

  • Input: nums = [-2, -1, 2, 1], k = 1
  • Output: 2
  • Explanation: The longest subarray with a sum of 1 is [-1, 2], which has a length of 2.

Example 3:

  • Input: nums = [3, 4, 7, 2, -3, 1, 4, 2], k = 7
  • Output: 4
  • Explanation: The longest subarray with a sum of 7 is [7, 2, -3, 1], which has a length of 4.

Constraints:

  • 1 <= nums.length <= 2 * 10^5
  • -10^4 <= nums[i] <= 10^4
  • -10^9 <= k <= 10^9

Solution

To solve this problem, we can use a hash map (or dictionary) to keep track of the cumulative sum at each index. The key idea is to use the cumulative sum to quickly determine the length of subarrays that sum up to k. By storing the earliest occurrence of each cumulative sum, we can efficiently check if there is a subarray ending at the current index with the required sum. This approach leverages the relationship between the cumulative sums to find the longest subarray with a sum of k in linear time.

This approach is efficient because it avoids the need for nested loops, which would result in a quadratic time complexity. Instead, by using a hash map to store the cumulative sums, we can achieve a linear time complexity, making the solution scalable for large input sizes.

Step-by-Step Algorithm

  1. Initialization:
    • Create an empty hash map (cumMap) to store cumulative sums and their earliest indices.
    • Initialize cumSum to 0 to keep track of the cumulative sum as we iterate through the array.
    • Initialize maxLen to 0 to keep track of the maximum length of the subarray with a sum of k.
  2. Iterate through the array:
    • Loop through each element in the nums array using a for loop:
      • Update the cumulative sum:
        • For each element num at index i, update the cumulative sum: cumSum += num.
      • Check if the cumulative sum equals k:
        • If cumSum == k, update maxLen to i + 1 since the entire array from the start to the current index sums to k.
      • Check for a subarray with a sum of k:
        • Calculate cumSum - k.
        • If (cumSum - k) exists in cumMap, it means there is a subarray that sums to k:
          • Update maxLen to the maximum of its current value and the length of this subarray: i - cumMap[cumSum - k].
      • Store the cumulative sum and its index:
        • If cumSum is not already in cumMap, add it with its index i: cumMap[cumSum] = i.
  3. Return the maximum length:
    • After the loop ends, return maxLen.

Algorithm Walkthrough

Using the input nums = [1, 2, 3, -2, 5], k = 5:

  1. Initialization:
    • cumMap = {}
    • cumSum = 0
    • maxLen = 0
  2. Iteration:
    • Index 0, num = 1:
      • Update the cumulative sum: cumSum = 1
      • Check if the cumulative sum equals k: cumSum != k
      • Check for a subarray with a sum of k: cumSum - k = -4 does not exist in cumMap
      • Store the cumulative sum and its index: Add 1 to cumMap: cumMap = {1: 0}
    • Index 1, num = 2:
      • Update the cumulative sum: cumSum = 3
      • Check if the cumulative sum equals k: cumSum != k
      • Check for a subarray with a sum of k: cumSum - k = -2 does not exist in cumMap
      • Store the cumulative sum and its index: Add 3 to cumMap: cumMap = {1: 0, 3: 1}
    • Index 2, num = 3:
      • Update the cumulative sum: cumSum = 6
      • Check if the cumulative sum equals k: cumSum != k
      • Check for a subarray with a sum of k: cumSum - k = 1 exists in cumMap at index 0
      • Update maxLen: maxLen = max(0, 2 - 0) = 2
      • Store the cumulative sum and its index: Add 6 to cumMap: cumMap = {1: 0, 3: 1, 6: 2}
    • Index 3, num = -2:
      • Update the cumulative sum: cumSum = 4
      • Check if the cumulative sum equals k: cumSum != k
      • Check for a subarray with a sum of k: cumSum - k = -1 does not exist in cumMap
      • Store the cumulative sum and its index: Add 4 to cumMap: cumMap = {1: 0, 3: 1, 6: 2, 4: 3}
    • Index 4, num = 5:
      • Update the cumulative sum: cumSum = 9
      • Check if the cumulative sum equals k: cumSum != k
      • Check for a subarray with a sum of k: cumSum - k = 4 exists in cumMap at index 3
      • Update maxLen: maxLen = max(2, 4 - 3) = 2
      • Store the cumulative sum and its index: Add 9 to cumMap: cumMap = {1: 0, 3: 1, 6: 2, 4: 3, 9: 4}
  3. Result:
    • The maximum length of a subarray summing to 5 is 2.

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
class Solution:
    def maxSubArrayLen(self, nums, k):
        # Create a dictionary to store cumulative sums and their earliest indices
        cum_map = {}
        cum_sum = 0  # Initialize cumulative sum
        max_len = 0  # Initialize max length of subarray with sum k

        # Iterate through the array
        for i in range(len(nums)):
            cum_sum += nums[i]  # Update cumulative sum

            # Check if cumulative sum equals k
            if cum_sum == k:
                max_len = i + 1  # Update max length

            # Check if there is a subarray with sum k
            if (cum_sum - k) in cum_map:
                max_len = max(max_len, i - cum_map[cum_sum - k])  # Update max length

            # Store the cumulative sum and its index
            if cum_sum not in cum_map:
                cum_map[cum_sum] = i

        return max_len  # Return the maximum length

if __name__ == "__main__":
    sol = Solution()

    # Test cases
    nums1 = [1, 2, 3, -2, 5]
    k1 = 5
    print(sol.maxSubArrayLen(nums1, k1))  # Output: 2

    nums2 = [-2, -1, 2, 1]
    k2 = 1
    print(sol.maxSubArrayLen(nums2, k2))  # Output: 2

    nums3 = [3, 4, 7, 2, -3, 1, 4, 2]
    k3 = 7
    print(sol.maxSubArrayLen(nums3, k3))  # Output: 4

Complexity Analysis

  • Time Complexity: The algorithm runs in O(n) time, where n is the number of elements in the array. This is because we traverse the array once and perform constant-time operations for each element.
  • Space Complexity: The space complexity is O(n) because, in the worst case, we may store each cumulative sum in the hash map.

Binary Subarrays With Sum

Problem Statement

Given a binary called nums and an integer called goal, return the number of subarrays that have a sum equal to goal.

A subarray is a part of the array that is continuous, meaning all its elements are next to each other.

Examples

Example 1

  • Input: nums = [1, 1, 0, 1, 1], goal = 2
  • Expected Output: 5
  • Justification: The subarrays with a sum of 3 are: [1, 1] (from index 0 to 1), [1, 1, 0] (from index 0 to 2), [1, 0, 1] (from index 1 to 3), [0, 1, 1] (from index 2 to 5), and [1, 1] (from index 4 to 5).

Example 2

  • Input: nums = [1, 1, 1, 1, 0, 0], goal = 3
  • Expected Output: 4
  • Justification: The subarrays with a sum of 3 are: [1, 1, 1] (from index 0 to 2), [1, 1, 1] (from index 1 to 3), [1, 1, 1, 0] (from index 1 to 4), and [1, 1, 1, 0, 0] (from index 1 to 5).

Example 3

  • Input: nums = [0, 0, 0, 0, 1, 0, 1], goal = 1
  • Expected Output: 12
  • Justification: The subarrays with a sum of 1 are: [0, 0, 0, 0, 1], [0, 0, 0, 1], [0, 0, 1], [0, 1], [1], [0, 0, 0, 0, 1, 0], [0, 0, 0, 1, 0], [0, 0, 1, 0], [0, 1, 0], [1, 0], [0, 1], and[1]`.

Solution

To solve this problem, we can use a technique called the prefix sum combined with a hashmap (or dictionary). The prefix sum helps in calculating the sum of elements in any subarray efficiently. We will keep a running total (prefix sum) as we iterate through the array. For each prefix sum, we will check if there is a previous prefix sum that, when subtracted from the current prefix sum, equals the goal. This way, we can count the subarrays that meet the requirement.

This approach works because it allows us to find the subarray sums in constant time by leveraging previously computed sums stored in the hashmap. This is efficient and avoids the need for a nested loop, reducing the time complexity from O(N^2) to O(N).

Step-by-step Algorithm

  • Initialize a variable count to 0. This will hold the number of subarrays that sum up to the goal.
  • Initialize a variable prefix_sum to 0. This will keep track of the sum of elements from the start up to the current position.
  • Initialize a hashmap (dictionary) prefix_sums with one entry {0: 1}. This accounts for subarrays that start from the beginning.
  • Iterate through each element in the array nums.
    • Add the current element to prefix_sum.
    • Check if prefix_sum - goal exists in the prefix_sums. If it does, add the value of prefix_sums[prefix_sum - goal] to count.
    • Increment the value of prefix_sum in prefix_sums by 1. If prefix_sum is not in the hashmap, set it to 1.
  • After the loop, count will hold the number of subarrays with a sum equal to goal.

Algorithm Walkthrough

Using the input nums = [1, 1, 0, 1, 1] and goal = 2:

  • Initialize count = 0, prefix_sum = 0, prefix_sums = {0: 1}
  • Iterate through nums:
    • Step 1: Current element 1
      • prefix_sum = 1
      • prefix_sum - goal = -1 (not in prefix_sums)
      • Update prefix_sums: {0: 1, 1: 1}
    • Step 2: Current element 1
      • prefix_sum = 2
      • prefix_sum - goal = 0 (exists in prefix_sums, add prefix_sums[0] to count)
      • count = 1
      • Update prefix_sums: {0: 1, 1: 1, 2: 1}
    • Step 3: Current element 0
      • prefix_sum = 2
      • prefix_sum - goal = 0 (exists in prefix_sums, add prefix_sums[0] to count)
      • count = 2
      • Update prefix_sums: {0: 1, 1: 1, 2: 2}
    • Step 4: Current element 1
      • prefix_sum = 3
      • prefix_sum - goal = 1 (exists in prefix_sums, add prefix_sums[1] to count)
      • count = 3
      • Update prefix_sums: {0: 1, 1: 1, 2: 2, 3: 1}
    • Step 5: Current element 1
      • prefix_sum = 4
      • prefix_sum - goal = 2 (exists in prefix_sums, add prefix_sums[2] to count)
      • count = 5
      • Update prefix_sums: {0: 1, 1: 1, 2: 2, 3: 1, 4: 1}

Final count is 5.

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Solution:
    def numSubarraysWithSum(self, nums, goal):
        count = 0  # Initialize count of subarrays
        prefix_sum = 0  # Initialize prefix sum
        prefix_sums = {0: 1}  # Initialize hashmap for prefix sums with initial prefix sum of 0

        for num in nums:
            prefix_sum += num  # Update prefix sum
            # If (prefix_sum - goal) exists in hashmap, it means we found a subarray with sum equals to goal
            if prefix_sum - goal in prefix_sums:
                count += prefix_sums[prefix_sum - goal]  # Update count of subarrays
            # Update the hashmap with current prefix sum
            if prefix_sum in prefix_sums:
                prefix_sums[prefix_sum] += 1
            else:
                prefix_sums[prefix_sum] = 1

        return count  # Return the count of subarrays

if __name__ == "__main__":
    sol = Solution()
    nums1 = [1, 1, 0, 1, 1]
    goal1 = 2
    print(sol.numSubarraysWithSum(nums1, goal1))  # Expected output: 5

    nums2 = [1, 1, 1, 1, 0, 0]
    goal2 = 3
    print(sol.numSubarraysWithSum(nums2, goal2))  # Expected output: 4

    nums3 = [0, 0, 0, 0, 1, 0, 1]
    goal3 = 1
    print(sol.numSubarraysWithSum(nums3, goal3))  # Expected output: 12

Complexity Analysis

Time Complexity

The time complexity of this algorithm is O(N), where n is the number of elements in the input array nums. This is because we iterate through the array once, and each operation inside the loop (like updating the prefix sum and hashmap) is done in constant time.

Space Complexity

The space complexity of this algorithm is O(N), where n is the number of elements in the input array nums. This is because, in the worst case, we might store every prefix sum in the hashmap. If all prefix sums are unique, the hashmap will have n entries.

Subarray Sums Divisible by K

Problem Statement

Given an array of integers nums and an integer k, return the count of non-empty subarrays that have a sum that is divisible by k.

A subarray is a continuous part of an array.

Examples

Example 1

  • Input: nums = [3, 1, 2, -2, 5, -1], k = 3
  • Expected Output: 7
  • Justification: The subarrays that sum to a multiple of 3 are [3], [1, 2], [3, 1, 2], [3, 1, 2, -2, 5], [1, 2, -2, 5], [-2, 5], and [2, -2].

Example 2

  • Input: nums = [4, 5, 0, -2, -3, 1], k = 5
  • Expected Output: 7
  • Justification: The subarrays that sum to a multiple of 5 are [5], [4, 5, 0, -2, -3, 1], [5, 0], [0], [5, 0, -2, -3], [0, -2, -3], and [-2, -3].

Example 3

  • Input: nums = [-1, 2, 9], k = 2
  • Expected Output: 2
  • Justification: The subarrays that sum to a multiple of 2 are [2] and [-1, 2, 9].

Constraints:

  • 1 <= nums.length <= 3 * 10^4
  • -10^4 <= nums[i] <= 10^4
  • 2 <= k <= 10^4

Solution

To solve this problem, we will use a hash map (dictionary) to keep track of the cumulative sums and their remainders when divided by k. This helps in finding the number of subarrays whose sum is divisible by k. The idea is to iterate through the array while maintaining a running sum. For each element, calculate the cumulative sum and its remainder when divided by k. If this remainder has been seen before, it indicates that there is a subarray which sum is divisible by k. By using the hash map to store and count these remainders, we efficiently count the subarrays without needing nested loops, making the approach more efficient.

This approach works because it leverages the properties of modular arithmetic to efficiently determine subarrays that meet the criteria. Using a hash map to store the counts of remainders enables us to quickly check for existing subarrays that, when combined with the current element, form a subarray whose sum is divisible by k.

Step-by-step Algorithm

  • Initialize a hash map remainder_count to store the frequency of remainders. Start with {0: 1} to handle cases where the subarray itself is divisible by k.
  • Initialize cumulative_sum to 0 and count to 0.
  • Iterate through each element in nums:
    • Add the current element to cumulative_sum.
    • Compute the remainder of cumulative_sum divided by k.
    • If the remainder is negative, adjust it by adding k.
    • If the remainder is already in remainder_count, increment count by the value associated with the remainder in the hash map.
    • Increment the count of this remainder in the hash map.
  • Return count.

Algorithm Walkthrough

Using the input = nums = [3, 1, 2, -2, 5, -1] and k = 3.

  1. Initialization:
    • remainder_count = {0: 1}
    • cumulative_sum = 0
    • count = 0
  2. Iteration 1 (num = 3):
    • cumulative_sum = 3
    • remainder = 3 % 3 = 0
    • count += remainder_count[0] = 1 -> count = 1
    • Update remainder_count: {0: 2}
  3. Iteration 2 (num = 1):
    • cumulative_sum = 4
    • remainder = 4 % 3 = 1
    • count += remainder_count.get(1, 0) = 0 -> count = 1
    • Update remainder_count: {0: 2, 1: 1}
  4. Iteration 3 (num = 2):
    • cumulative_sum = 6
    • remainder = 6 % 3 = 0
    • count += remainder_count[0] = 2 -> count = 3
    • Update remainder_count: {0: 3, 1: 1}
  5. Iteration 4 (num = -2):
    • cumulative_sum = 4
    • remainder = 4 % 3 = 1
    • count += remainder_count[1] = 1 -> count = 4
    • Update remainder_count: {0: 3, 1: 2}
  6. Iteration 5 (num = 5):
    • cumulative_sum = 9
    • remainder = 9 % 3 = 0
    • count += remainder_count[0] = 3 -> count = 7
    • Update remainder_count: {0: 4, 1: 2}
  7. Iteration 6 (num = -1):
    • cumulative_sum = 8
    • remainder = 8 % 3 = 2
    • count += remainder_count.get(2, 0) = 0 -> count = 7
    • Update remainder_count: {0: 4, 1: 2, 2: 1}

The total count of subarrays whose sum is divisible by k is 7.

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
class Solution:
    def subarraysDivByK(self, nums, k):
        # Create a dictionary to store the frequency of remainders
        remainder_count = {0: 1}
        # Initialize cumulative sum and count of subarrays
        cumulative_sum = 0
        count = 0

        # Loop through each number in the array
        for num in nums:
            # Add the current number to the cumulative sum
            cumulative_sum += num
            # Calculate the remainder of cumulative sum divided by k
            remainder = cumulative_sum % k
            # If remainder is negative, adjust it by adding k
            if remainder < 0:
                remainder += k

            # If this remainder has been seen before, add its frequency to the count
            count += remainder_count.get(remainder, 0)
            # Update the frequency of this remainder in the dictionary
            remainder_count[remainder] = remainder_count.get(remainder, 0) + 1

        # Return the total count of subarrays
        return count

if __name__ == "__main__":
    solution = Solution()

    # Example 1
    nums1 = [3, 1, 2, -2, 5, -1]
    k1 = 3
    print(solution.subarraysDivByK(nums1, k1)) # 7

    # Example 2
    nums2 = [4, 5, 0, -2, -3, 1]
    k2 = 5
    print(solution.subarraysDivByK(nums2, k2)) # 7

    # Example 3
    nums3 = [-1, 2, 9]
    k3 = 2
    print(solution.subarraysDivByK(nums3, k3)) # 2

Complexity Analysis

Time Complexity

The time complexity of the algorithm is O(N), where (n) is the number of elements in the input array nums. This is because we traverse the array exactly once, performing constant-time operations for each element.

Space Complexity

The space complexity of the algorithm is O(K), where (k) is the value of the divisor. This is due to the hash map (or dictionary) that stores at most (k) different remainders. In the worst case, the hash map will store all possible remainders from (0) to (k-1).

Sum of Absolute Differences in a Sorted Array

Problem Statement

Given an integer array nums sorted in increasing order, return an array result of the same length, where result[i] should be the sum of the absolute differences between nums[i] and every other element in nums.

Examples

Example 1

  • Input: [1, 3, 6]
  • Output: [7, 5, 8]
  • Explanation:
    • For result[0]: |1-3| + |1-6| = 2 + 5 = 7
    • For result[1]: |3-1| + |3-6| = 2 + 3 = 5
    • For result[2]: |6-1| + |6-3| = 5 + 3 = 8

Example 2

  • Input: [2, 4, 7]
  • Output: [7, 5, 8]
  • Explanation:
    • For result[0]: |2-4| + |2-7| = 2 + 5 = 7
    • For result[1]: |4-2| + |4-7| = 2 + 3 = 5
    • For result[2]: |7-2| + |7-4| = 5 + 3 = 8

Example 3

  • Input: [1, 2, 4, 5]
  • Output: [8, 6, 6, 6]
  • Explanation:
    • For result[0]: |1-2| + |1-4| + |1-5| = 1 + 3 + 4 = 8
    • For result[1]: |2-1| + |2-4| + |2-5| = 1 + 2 + 3 = 6
    • For result[2]: |4-1| + |4-2| + |4-5| = 3 + 2 + 1 = 6
    • For result[3]: |5-1| + |5-2| + |5-4| = 4 + 3 + 1 = 8

Constraints:

  • 2 <= nums.length <= 105
  • 1 <= nums[i] <= nums[i + 1] <= 104

Solution

To solve this problem, we need to calculate the sum of absolute differences for each element in the array. We can simplify this by using prefix sums to avoid repeatedly calculating the same differences. By leveraging prefix sums, we can compute the total difference more efficiently.

For each element, we will split the array into two parts: the left part and the right part. The left part includes all elements before the current one, and the right part includes all elements after the current one. Using the prefix sums, we can quickly get the sum of elements on the left and right, then use these sums to calculate the absolute differences. This method avoids the need for nested loops and reduces the time complexity.

Step-by-step Algorithm

  1. Initialize Arrays:
    • Create an array result of the same length as nums initialized to zero.
    • Create an array prefixSum of length n + 1 (where n is the length of nums) initialized to zero.
  2. Calculate Prefix Sums:
    • Iterate through the nums array.
    • For each index i, compute prefixSum[i + 1] = prefixSum[i] + nums[i].
    • This gives us the sum of all elements from the start up to index i.
  3. Compute Result Array:
    • Iterate through the nums array.
    • For each index i:
      • Calculate the sum of the left part using prefixSum[i].
      • Calculate the sum of the right part using prefixSum[n] - prefixSum[i + 1].
      • Compute result[i] using the formula:
        • result[i] = (i * nums[i] - leftSum) + (rightSum - (n - i - 1) * nums[i])
      • The left part is i * nums[i] - leftSum.
      • The right part is rightSum - (n - i - 1) * nums[i].
  4. Return Result:
    • Return the result array.

Algorithm Walkthrough

Let’s consider the input: nums = {1, 2, 4, 5}

  1. Initialize Arrays:

    • nums = [1, 2, 4, 5]
    • result = [0, 0, 0, 0]
    • prefixSum = [0, 0, 0, 0, 0]

  2. Calculate Prefix Sums:

    • For i = 0, prefixSum[1] = prefixSum[0] + nums[0] = 0 + 1 = 1
      • prefixSum = [0, 1, 0, 0, 0]
    • For i = 1, prefixSum[2] = prefixSum[1] + nums[1] = 1 + 2 = 3
      • prefixSum = [0, 1, 3, 0, 0]
    • For i = 2, prefixSum[3] = prefixSum[2] + nums[2] = 3 + 4 = 7
      • prefixSum = [0, 1, 3, 7, 0]
    • For i = 3, prefixSum[4] = prefixSum[3] + nums[3] = 7 + 5 = 12
      • prefixSum = [0, 1, 3, 7, 12]

  3. Compute Result Array:

    • For i = 0:

      • leftSum = prefixSum[0] = 0

      • rightSum = prefixSum[4] - prefixSum[1] = 12 - 1 = 11

      • ```
        result[0] = (0 1 - 0) + (11 - 3 1) = 0 + 8 = 8

        1
        2
        3
        4
        5
        6
        7
        8
        9
        10
        11

            - `result = [8, 0, 0, 0]`

        - For `i = 1`:

          - `leftSum = prefixSum[1] = 1`

          - `rightSum = prefixSum[4] - prefixSum[2] = 12 - 3 = 9`

          - ```
            result[1] = (1 * 2 - 1) + (9 - 2 * 2) = 1 + 5 = 6
        • result = [8, 6, 0, 0]

    • For i = 2:

      • leftSum = prefixSum[2] = 3

      • rightSum = prefixSum[4] - prefixSum[3] = 12 - 7 = 5

      • ```
        result[2] = (2 4 - 3) + (5 - 1 4) = 5 + 1 = 6

        1
        2
        3
        4
        5
        6
        7
        8
        9
        10
        11

            - `result = [8, 6, 6, 0]`

        - For `i = 3`:

          - `leftSum = prefixSum[3] = 7`

          - `rightSum = prefixSum[4] - prefixSum[4] = 12 - 12 = 0`

          - ```
            result[3] = (3 * 5 - 7) + (0 - 0 * 5) = 8 + 0 = 8
        • result = [8, 6, 6, 8]

  4. Return Result:

    • The final result array is [8, 6, 6, 8].

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution:
    def getSumAbsoluteDifferences(self, nums):
        n = len(nums)
        result = [0] * n
        prefix_sum = [0] * (n + 1)

        # Calculate prefix sums
        for i in range(n):
            prefix_sum[i + 1] = prefix_sum[i] + nums[i]

        # Calculate result array
        for i in range(n):
            left_sum = prefix_sum[i]
            right_sum = prefix_sum[n] - prefix_sum[i + 1]
            result[i] = i * nums[i] - left_sum + right_sum - (n - i - 1) * nums[i]

        return result

if __name__ == "__main__":
    sol = Solution()
    example1 = [1, 3, 6]
    example2 = [2, 4, 7]
    example3 = [1, 2, 4, 5]

    print(sol.getSumAbsoluteDifferences(example1))  # [7, 5, 8]
    print(sol.getSumAbsoluteDifferences(example2))  # [7, 5, 8]
    print(sol.getSumAbsoluteDifferences(example3))  # [8, 6, 6, 8]

Complexity Analysis

Time Complexity

  • Prefix Sum Calculation: We iterate through the array once to calculate the prefix sums, which takes O(n) time.
  • Result Calculation: We iterate through the array once more to compute the result for each element, which also takes O(n) time.

Thus, the overall time complexity is O(n), where n is the length of the input array.

Space Complexity

  • We use an extra array of size n+1 for the prefix sums.
  • We also use an extra array of size n for the result.

Thus, the overall space complexity is O(n).

Subarray Sum Equals K

Problem Statement

Given an array nums containing n integers and integer k, return the total number of subarrays having sum equal to k.

A subarray is defined as a contiguous non-empty sequence of the array elements.

Examples

Example 1:

  • Input: nums = [1, 2, 3], k = 3
  • Expected Output: 2
  • Justification: There are two subarrays that sum to 3: [1, 2] and [3].

Example 2:

  • Input: nums = [10, 2, -2, -20, 10], k = -10
  • Expected Output: 3
  • Justification: Three subarrays sum up to -10: [10, 2, -2, -20], [2, -2, -20, 10], and [-20, 10].

Example 3:

  • Input: nums = [5, 1, 2, -3, 4, -2], k = 3
  • Expected Output: 2
  • Justification: There are two subarrays that sum to 3: [2, -3, 4], and [1, 2].

Solution

To solve this problem, we’ll employ a technique that involves using a hashmap to efficiently track the cumulative sum of elements as we iterate through the array. The core idea is that if the cumulative sum up to two indices, say i and j, differs by the target value k, then the sum of the elements lying between i and j is k.

The algorithm will iterate through the array, calculating the cumulative sum at each step. We then check if (cumulative sum - k) is present in the hashmap. If it is, it means there exists a previous cumulative sum such that the difference between the current sum and that sum equals k, indicating a valid subarray. We add the count of these occurrences to our total. Additionally, we keep updating the hashmap with the count of each cumulative sum encountered. This approach is effective as it allows us to find the required subarrays in a single pass through the array, making it efficient in terms of time complexity.

Step-by-step Algorithm

  • Initialize a variable count to 0 and a hashmap cumulativeSumFrequency with a key-value pair (0:1) to handle edge cases.
  • Iterate through the array nums while keeping track of the cumulativeSum.
  • For each element num in nums:
    • Add num to cumulativeSum.
    • Check if (cumulativeSum - k) is in cumulativeSumFrequency. If it is, add its frequency to count.
    • Update cumulativeSumFrequency by incrementing the count of cumulativeSum.
  • Return the value of count.

Algorithm Walkthrough

Let’s walk through the algorithm with Example 2: nums = [10, 2, -2, -20, 10], k = -10.

  • Start with cumulativeSum = 0, count = 0, cumulativeSumFrequency = {0: 1}.
  • For num = 10: cumulativeSum = 10. (cumulativeSum - k) = 20 is not in cumulativeSumFrequency. Update cumulativeSumFrequency to {0: 1, 10: 1}.
  • For num = 2: cumulativeSum = 12. (cumulativeSum - k) = 22 is not in cumulativeSumFrequency. Update cumulativeSumFrequency to {0: 1, 10: 1, 12: 1}.
  • For num = -2: cumulativeSum = 10. (cumulativeSum - k) = 20 is not in cumulativeSumFrequency. Update cumulativeSumFrequency to {0: 1, 10: 2, 12: 1}.
  • For num = -20: cumulativeSum = -10. (cumulativeSum - k) = 0 is in cumulativeSumFrequency. Add 1 to count. Update cumulativeSumFrequency to {0: 1, 10: 2, 12: 1, -10: 1}.
  • For num = 10: cumulativeSum = 0. (cumulativeSum - k) = 10 is in cumulativeSumFrequency with frequency 2.

Add 2 to count. Update cumulativeSumFrequency to {0: 2, 10: 2, 12: 1, -10: 1}.

  • Final count is 3.

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution:
    def subarraySum(self, nums, k):
        count, cumulative_sum, cumulative_sum_frequency = 0, 0, {0: 1}

        for num in nums:
            cumulative_sum += num  # Update cumulative sum
            # Check if there's a subarray sum that equals k
            count += cumulative_sum_frequency.get(cumulative_sum - k, 0)
            # Update the frequency map for the current cumulative sum
            cumulative_sum_frequency[cumulative_sum] = cumulative_sum_frequency.get(cumulative_sum, 0) + 1

        return count  # Return the total count of subarrays

# Testing with the provided examples
solution = Solution()
print(solution.subarraySum([1, 2, 3], 3))  # Example 1
print(solution.subarraySum([10, 2, -2, -20, 10], -10))  # Example 2
print(solution.subarraySum([5, 1, 2, -3, 4, -2], 3))  # Example 3

Complexity Analysis

  • Time Complexity: O(n), where n is the length of the input array. This is due to a single loop through the array and constant-time hashmap operations.
  • Space Complexity: O(n), where n is the length of the input array. The primary space usage is the hashmap storing the cumulative sum frequencies, which in the worst case can grow to the size of the array.

Author：Hasuer

Link：https://hasuer.github.io/27-pattern-prefix-sum/index.html

Publish date：May 27th 2024, 2:29:54 pm

Update date：May 28th 2024, 11:31:20 am

License：本文采用知识共享署名-非商业性使用 4.0 国际许可协议进行许可

CATALOG
  1. 1. Introduction Prefix Sum Pattern
    1. 1.1. What is Prefix Sum?
      1. 1.1.1. Algorithm to Calculate Prefix Sum
      2. 1.1.2. Code
      3. 1.1.3. Complexity Analysis
        1. 1.1.3.1. Time Complexity
        2. 1.1.3.2. Space Complexity
    2. 1.2. Why Use Prefix Sums?
      1. 1.2.1. Example: Range Sum Query
        1. 1.2.1.1. Example
        2. 1.2.1.2. Step-by-Step Algorithm
        3. 1.2.1.3. Code
        4. 1.2.1.4. Complexity Analysis
    3. 1.3. Applications of Prefix Sums
  2. 2. Find the Middle Index in Array
    1. 2.1. Problem Statement
      1. 2.1.1. Examples
    2. 2.2. Solution
      1. 2.2.1. Step-by-step Algorithm
      2. 2.2.2. Algorithm Walkthrough
    3. 2.3. Code
    4. 2.4. Complexity Analysis
  3. 3. Left and Right Sum Differences (easy)
    1. 3.1. Problem Statement
      1. 3.1.1. Examples
    2. 3.2. Solution
      1. 3.2.1. Algorithm Walkthrough
    3. 3.3. Code
    4. 3.4. Time Complexity
    5. 3.5. Space Complexity
  4. 4. Maximum Size Subarray Sum Equals k
    1. 4.1. Problem Statement
      1. 4.1.1. Examples
    2. 4.2. Solution
      1. 4.2.1. Step-by-Step Algorithm
      2. 4.2.2. Algorithm Walkthrough
    3. 4.3. Code
    4. 4.4. Complexity Analysis
  5. 5. Binary Subarrays With Sum
    1. 5.1. Problem Statement
      1. 5.1.1. Examples
    2. 5.2. Solution
      1. 5.2.1. Step-by-step Algorithm
      2. 5.2.2. Algorithm Walkthrough
    3. 5.3. Code
    4. 5.4. Complexity Analysis
      1. 5.4.1. Time Complexity
      2. 5.4.2. Space Complexity
  6. 6. Subarray Sums Divisible by K
    1. 6.1. Problem Statement
      1. 6.1.1. Examples
    2. 6.2. Solution
      1. 6.2.1. Step-by-step Algorithm
      2. 6.2.2. Algorithm Walkthrough
    3. 6.3. Code
    4. 6.4. Complexity Analysis
      1. 6.4.1. Time Complexity
      2. 6.4.2. Space Complexity
  7. 7. Sum of Absolute Differences in a Sorted Array
    1. 7.1. Problem Statement
      1. 7.1.1. Examples
    2. 7.2. Solution
      1. 7.2.1. Step-by-step Algorithm
      2. 7.2.2. Algorithm Walkthrough
    3. 7.3. Code
    4. 7.4. Complexity Analysis
      1. 7.4.1. Time Complexity
      2. 7.4.2. Space Complexity
  8. 8. Subarray Sum Equals K
    1. 8.1. Problem Statement
      1. 8.1.1. Examples
    2. 8.2. Solution
      1. 8.2.1. Step-by-step Algorithm
      2. 8.2.2. Algorithm Walkthrough
    3. 8.3. Code
    4. 8.4. Complexity Analysis
Total : 41
2024
2022
2021
Interview
技术笔记 Grokking-Interview-Pattern