Hasuer's Studio.

16. Pattern Modified Binary Search

Grokking Interview Pattern Interview
Word count: 7.1kReading time: 44 min
2024/05/16

Introduction

As we know, whenever we are given a sorted Array or LinkedList or Matrix, and we are asked to find a certain element, the best algorithm we can use is the Binary Search.

This pattern describes an efficient way to handle all problems involving Binary Search. We will go through a set of problems that will help us build an understanding of this pattern so that we can apply this technique to other problems we might come across in the interviews.

Let’s start with our first problem.

Order-agnostic Binary Search (easy)

704. Binary Search Design Gurus Educative.io

Problem Statement

Given a sorted array of numbers, find if a given number ‘key’ is present in the array. Though we know that the array is sorted, we don’t know if it’s sorted in ascending or descending order. You should assume that the array can have duplicates.

Write a function to return the index of the ‘key’ if it is present in the array, otherwise return -1.

Example 1:

1
2
Input: [4, 6, 10], key = 10
Output: 2

Example 2:

1
2
Input: [1, 2, 3, 4, 5, 6, 7], key = 5
Output: 4

Example 3:

1
2
Input: [10, 6, 4], key = 10
Output: 0

Example 4:

1
2
Input: [10, 6, 4], key = 4
Output: 2

Constraints:

  • 1 <= nums.length <= 10^4
  • -10^4 < nums[i], target < 10^4

Solution

To make things simple, let’s first solve this problem assuming that the input array is sorted in ascending order. Here are the set of steps for Binary Search:

  1. Let’s assume start is pointing to the first index and end is pointing to the last index of the input array (let’s call it arr). This means:
1
2
int start = 0;
int end = arr.length - 1;
  1. First, we will find the middle of start and end. An easy way to find the middle would be: middle=(start+end)/2. For Java and C++, this equation will work for most cases, but when start or end is large, this equation will give us the wrong result due to integer overflow. Imagine that start is equal to the maximum range of an integer (e.g. for Java: int start = Integer.MAX_VALUE). Now adding anything to start will result in an integer overflow. Since we need to add both the numbers first to evaluate our equation, an overflow might occur. The safest way to find the middle of two numbers without getting an overflow is as follows:
1
middle  = start + (end-start)/2

The above discussion is not relevant for Python, as we don’t have the integer overflow problem in pure Python.

  1. Next, we will see if the ‘key’ is equal to the number at index middle. If it is equal we return middle as the required index.

  2. If ‘key’ is not equal to number at index middle, we have to check two things:

    • If key < arr[middle], then we can conclude that the key will be smaller than all the numbers after index middle as the array is sorted in the ascending order. Hence, we can reduce our search to end = mid - 1.

    • If key > arr[middle], then we can conclude that the key will be greater than all numbers before index middle as the array is sorted in the ascending order. Hence, we can reduce our search to start = mid + 1.

  3. We will repeat steps 2-4 with new ranges of start to end. If at any time start becomes greater than end, this means that we can’t find the ‘key’ in the input array and we must return ‘-1’.

Here is the visual representation of Binary Search for the Example-2:

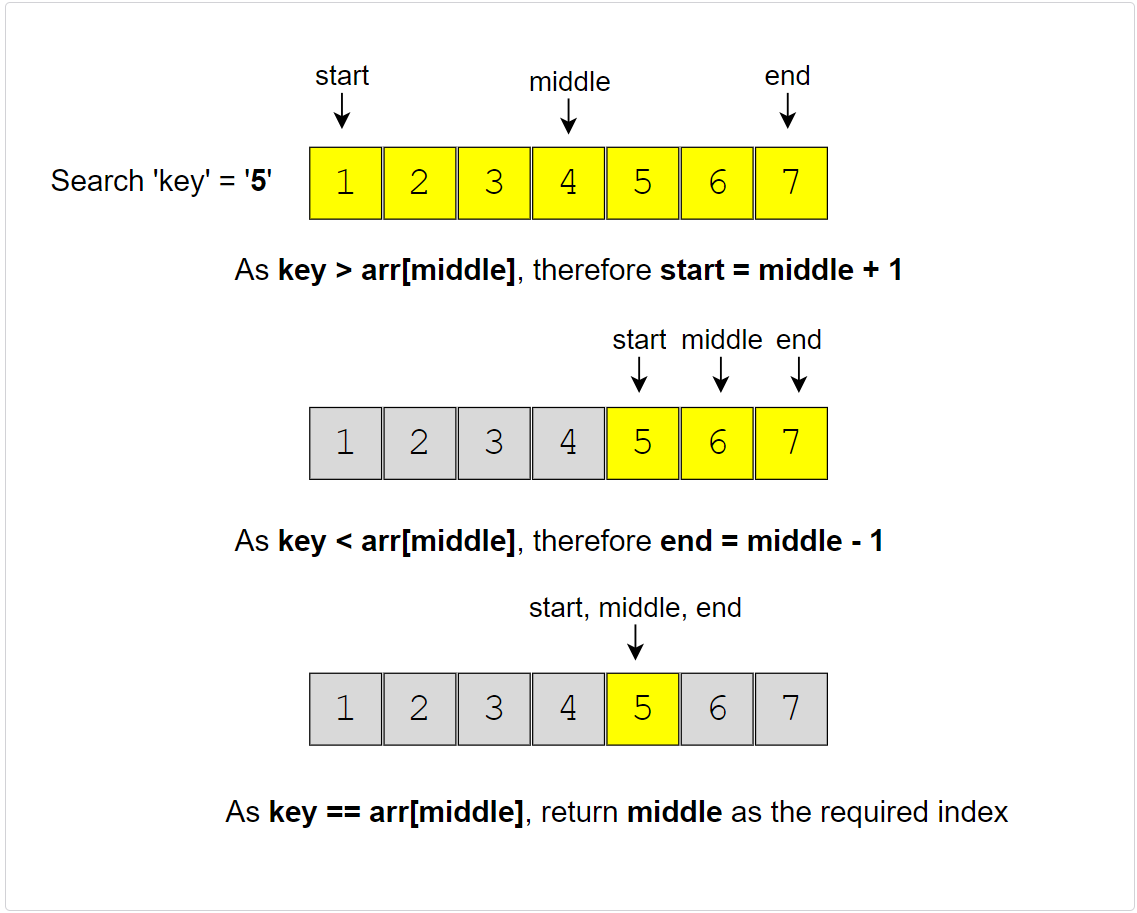
If the array is sorted in the descending order, we have to update the step 4 above as:

  • If key > arr[middle], then we can conclude that the key will be greater than all numbers after index middle as the array is sorted in the descending order. Hence, we can reduce our search to end = mid - 1.
  • If key < arr[middle], then we can conclude that the key will be smaller than all the numbers before index middle as the array is sorted in the descending order. Hence, we can reduce our search to start = mid + 1.

Finally, how can we figure out the sort order of the input array? We can compare the numbers pointed out by start and end index to find the sort order. If arr[start] < arr[end], it means that the numbers are sorted in ascending order otherwise they are sorted in the descending order.

Code

Here is what our algorithm will look like:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class Solution:
    def search(self, arr, key):
        start, end = 0, len(arr) - 1
        isAscending = arr[start] < arr[end]
        while start <= end:
            # calculate the middle of the current range
            mid = start + (end - start) // 2

            if key == arr[mid]:
                return mid

            if isAscending:  # ascending order
                if key < arr[mid]:
                    end = mid - 1  # the 'key' can be in the first half
                else:  # key > arr[mid]
                    start = mid + 1  # the 'key' can be in the second half
            else:  # descending order
                if key > arr[mid]:
                    end = mid - 1  # the 'key' can be in the first half
                else:  # key < arr[mid]
                    start = mid + 1  # the 'key' can be in the second half

        return -1  # element not found


def main():
    sol = Solution()
    print(sol.search([4, 6, 10], 10))
    print(sol.search([1, 2, 3, 4, 5, 6, 7], 5))
    print(sol.search([10, 6, 4], 10))
    print(sol.search([10, 6, 4], 4))


main()

Time complexity

Since, we are reducing the search range by half at every step, this means that the time complexity of our algorithm will be O(logN) where ‘N’ is the total elements in the given array.

Space complexity

The algorithm runs in constant space O(1).

Ceiling of a Number (medium)

Similar | Top Interview 150 | 35. Search Insert Position Design Gurus Educative.io

Problem Statement

Given an array of numbers sorted in an ascending order, find the ceiling of a given number ‘key’. The ceiling of the ‘key’ will be the smallest element in the given array greater than or equal to the ‘key’.

Write a function to return the index of the ceiling of the ‘key’. If there isn’t any ceiling return -1.

Example 1:

1
2
3
Input: [4, 6, 10], key = 6
Output: 1
Explanation: The smallest number greater than or equal to '6' is '6' having index '1'.

Example 2:

1
2
3
Input: [1, 3, 8, 10, 15], key = 12
Output: 4
Explanation: The smallest number greater than or equal to '12' is '15' having index '4'.

Example 3:

1
2
3
Input: [4, 6, 10], key = 17
Output: -1
Explanation: There is no number greater than or equal to '17' in the given array.

Example 4:

1
2
3
Input: [4, 6, 10], key = -1
Output: 0
Explanation: The smallest number greater than or equal to '-1' is '4' having index '0'.

Constraints:

  • 1 <= arr.length <= 10^4
  • -10^4 < arr[i], key < 10^4

Solution

This problem follows the Binary Search pattern. Since Binary Search helps us find a number in a sorted array efficiently, we can use a modified version of the Binary Search to find the ceiling of a number.

We can use a similar approach as discussed in Order-agnostic Binary Search. We will try to search for the ‘key’ in the given array. If we find the ‘key’, we return its index as the ceiling. If we can’t find the ‘key’, the next big number will be pointed out by the index start. Consider Example-2 mentioned above:

Since we are always adjusting our range to find the ‘key’, when we exit the loop, the start of our range will point to the smallest number greater than the ‘key’ as shown in the above picture.

We can add a check in the beginning to see if the ‘key’ is bigger than the biggest number in the input array. If so, we can return ‘-1’.

Code

Here is what our algorithm will look like:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
# 如果不存在key,那么退出循环的时候arr[start] > key > arr[end]
class Solution:
    def searchCeilingOfANumber(self, arr, key):
        n = len(arr)
        if key > arr[n - 1]:  # if the 'key' is bigger than the biggest element
            return -1

        start, end = 0, n - 1
        while start <= end:
            mid = start + (end - start) // 2
            if key < arr[mid]:
                end = mid - 1
            elif key > arr[mid]:
                start = mid + 1
            else:  # found the key
                return mid

        # since the loop is running until 'start <= end', so at the end of the while loop, 
        # 'start == end+1' we are not able to find the element in the given array, so the next
        # big number will be arr[start]
        return start


def main():
    sol = Solution()
    print(sol.searchCeilingOfANumber([4, 6, 10], 6))
    print(sol.searchCeilingOfANumber([1, 3, 8, 10, 15], 12))
    print(sol.searchCeilingOfANumber([4, 6, 10], 17))
    print(sol.searchCeilingOfANumber([4, 6, 10], -1))


main()

Time complexity

Since we are reducing the search range by half at every step, this means that the time complexity of our algorithm will be O(logN) where ‘N’ is the total elements in the given array.

Space complexity

The algorithm runs in constant space O(1).

Similar Problems

Problem 1

Given an array of numbers sorted in ascending order, find the floor of a given number ‘key’. The floor of the ‘key’ will be the biggest element in the given array smaller than or equal to the ‘key’

Write a function to return the index of the floor of the ‘key’. If there isn’t a floor, return -1.

Example 1:

1
2
3
Input: [4, 6, 10], key = 6
Output: 1
Explanation: The biggest number smaller than or equal to '6' is '6' having index '1'.

Example 2:

1
2
3
Input: [1, 3, 8, 10, 15], key = 12
Output: 3
Explanation: The biggest number smaller than or equal to '12' is '10' having index '3'.

Example 3:

1
2
3
Input: [4, 6, 10], key = 17
Output: 2
Explanation: The biggest number smaller than or equal to '17' is '10' having index '2'.

Example 4:

1
2
3
Input: [4, 6, 10], key = -1
Output: -1
Explanation: There is no number smaller than or equal to '-1' in the given array.

Code

The code is quite similar to the above solution; only the highlighted lines have changed:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution:
    def searchFloorOfANumber(self, arr, key):
        if key < arr[0]:  # if the 'key' is smaller than the smallest element
            return -1

        start, end = 0, len(arr) - 1
        while start <= end:
            mid = start + (end - start) // 2
            if key < arr[mid]:
                end = mid - 1
            elif key > arr[mid]:
                start = mid + 1
            else:  # found the key
                return mid

        # since the loop is running until 'start <= end', so at the end of the while loop, 
        # 'start == end+1' we are not able to find the element in the given array, so the next 
        # smaller number will be arr[end]
        return end


def main():
    sol = Solution()
    print(sol.searchFloorOfANumber([4, 6, 10], 6))
    print(sol.searchFloorOfANumber([1, 3, 8, 10, 15], 12))
    print(sol.searchFloorOfANumber([4, 6, 10], 17))
    print(sol.searchFloorOfANumber([4, 6, 10], -1))


main()

Next Letter (medium)

744. Find Smallest Letter Greater Than Target Design Gurus Educative.io

Problem Statement

Given an array of lowercase letters sorted in ascending order, find the smallest letter in the given array greater than a given ‘key’.

Assume the given array is a circular list, which means that the last letter is assumed to be connected with the first letter. This also means that the smallest letter in the given array is greater than the last letter of the array and is also the first letter of the array.

Write a function to return the next letter of the given ‘key’.

Example 1:

1
2
3
Input: ['a', 'c', 'f', 'h'], key = 'f'
Output: 'h'
Explanation: The smallest letter greater than 'f' is 'h' in the given array.

Example 2:

1
2
3
Input: ['a', 'c', 'f', 'h'], key = 'b'
Output: 'c'
Explanation: The smallest letter greater than 'b' is 'c'.

Example 3:

1
2
3
Input: ['a', 'c', 'f', 'h'], key = 'm'
Output: 'a'
Explanation: As the array is assumed to be circular, the smallest letter greater than 'm' is 'a'.

Example 4:

1
2
3
Input: ['a', 'c', 'f', 'h'], key = 'h'
Output: 'a'
Explanation: As the array is assumed to be circular, the smallest letter greater than 'h' is 'a'.

Constraints:

  • 2 <= letters.length <= 10^4
  • letters[i] is a lowercase English letter.
  • letters is sorted in non-decreasing order.
  • letters contains at least two different characters.
  • key is a lowercase English letter.

Solution

The problem follows the Binary Search pattern. Since Binary Search helps us find an element in a sorted array efficiently, we can use a modified version of it to find the next letter.

We can use a similar approach as discussed in Ceiling of a Number. There are a couple of differences though:

  1. The array is considered circular, which means if the ‘key’ is bigger than the last letter of the array or if it is smaller than the first letter of the array, the key’s next letter will be the first letter of the array.
  2. The other difference is that we have to find the next biggest letter which can’t be equal to the ‘key’. This means that we will ignore the case where key == arr[middle]. To handle this case, we can update our start range to start = middle +1.

In the end, instead of returning the element pointed out by start, we have to return the letter pointed out by start % array_length. This is needed because of point 2 discussed above. Imagine that the last letter of the array is equal to the ‘key’. In that case, we have to return the first letter of the input array.

Code

Here is what our algorithm will look like; the most important changes are in the highlighted lines:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
# 如果存在多个key,那么推出循环的时候letters[start] = key > letters[end]
class Solution:
    def searchNextLetter(self, letters, key):
        n = len(letters)

        start, end = 0, n - 1
        while start <= end:
            mid = start + (end - start) // 2
            if key < letters[mid]:
                end = mid - 1
            else:  # key >= letters[mid]:
                # 要是把key == letters[mid] 单独提出来，会有问题
                # 比如这个例子["e", "e", "e", "e", "e", "e", "n", "n", "n", "n"], 'e'
                start = mid + 1

        # since the loop is running until 'start <= end', so at the end of the while loop,
        # 'start == end+1'
        return letters[start % n]


def main():
    sol = Solution()
    print(sol.searchNextLetter(['a', 'c', 'f', 'h'], 'f'))
    print(sol.searchNextLetter(['a', 'c', 'f', 'h'], 'b'))
    print(sol.searchNextLetter(['a', 'c', 'f', 'h'], 'm'))


main()

Time complexity

Since, we are reducing the search range by half at every step, this means that the time complexity of our algorithm will be O(logN) where ‘N’ is the total elements in the given array.

Space complexity

The algorithm runs in constant space O(1).

#Number Range (medium)

Top Interview 150 | 34. Find First and Last Position of Element in Sorted Array Design Gurus Educative.io

Problem Statement

Given an array of numbers sorted in ascending order, find the range of a given number ‘key’. The range of the ‘key’ will be the first and last position of the ‘key’ in the array.

Write a function to return the range of the ‘key’. If the ‘key’ is not present return [-1, -1].

Example 1:

1
2
Input: [4, 6, 6, 6, 9], key = 6
Output: [1, 3]

Example 2:

1
2
Input: [1, 3, 8, 10, 15], key = 10
Output: [3, 3]

Example 3:

1
2
Input: [1, 3, 8, 10, 15], key = 12
Output: [-1, -1]

Constraints:

  • 0 <= nums.length <= 10^5
  • -10^9 <= nums[i] <= 10^9
  • nums is a non-decreasing array.
  • -10^9 <= target <= 10^9

Solution

The problem follows the Binary Search pattern. Since Binary Search helps us find a number in a sorted array efficiently, we can use a modified version of the Binary Search to find the first and the last position of a number.

We can use a similar approach as discussed in Order-agnostic Binary Search. We will try to search for the ‘key’ in the given array; if the ‘key’ is found (i.e. key == arr[middle) we have two options:

  1. When trying to find the first position of the ‘key’, we can update end = middle - 1 to see if the key is present before middle.
  2. When trying to find the last position of the ‘key’, we can update start = middle + 1 to see if the key is present after middle.

In both cases, we will keep track of the last position where we found the ‘key’. These positions will be the required range.

Code

Here is what our algorithm will look like:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
class Solution:
    def findRange(self, arr, key):
        result = [- 1, -1]
        result[0] = self.binary_search(arr, key, False)
        if result[0] != -1:  # no need to search, if 'key' is not present in the input array
            result[1] = self.binary_search(arr, key, True)
        return result

    # modified Binary Search
    def binary_search(self, arr, key, findMaxIndex):
        keyIndex = -1
        start, end = 0, len(arr) - 1
        while start <= end:
            mid = start + (end - start) // 2
            if key < arr[mid]:
                end = mid - 1
            elif key > arr[mid]:
                start = mid + 1
            else:  # key == arr[mid]
                keyIndex = mid
                if findMaxIndex:
                    start = mid + 1  # search ahead to find the last index of 'key'
                else:
                    end = mid - 1  # search behind to find the first index of 'key'

        return keyIndex


def main():
    sol = Solution()
    print(sol.findRange([4, 6, 6, 6, 9], 6))
    print(sol.findRange([1, 3, 8, 10, 15], 10))
    print(sol.findRange([1, 3, 8, 10, 15], 12))


main()

Time complexity

Since, we are reducing the search range by half at every step, this means that the time complexity of our algorithm will be O(logN) where ‘N’ is the total elements in the given array.

Space complexity

The algorithm runs in constant space O(1).

#Search in a Sorted Infinite Array (medium)

Leetcode 702 会员 Design Gurus Educative.io

Problem Statement

Given an infinite sorted array (or an array with unknown size), find if a given number ‘key’ is present in the array. Write a function to return the index of the ‘key’ if it is present in the array, otherwise return -1.

Since it is not possible to define an array with infinite (unknown) size, you will be provided with an interface ArrayReader to read elements of the array. ArrayReader.get(index) will return the number at index; if the array’s size is smaller than the index, it will return Integer.MAX_VALUE.

Example 1:

1
2
3
Input: [4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30], key = 16
Output: 6
Explanation: The key is present at index '6' in the array.

Example 2:

1
2
3
Input: [4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30], key = 11
Output: -1
Explanation: The key is not present in the array.

Example 3:

1
2
3
Input: [1, 3, 8, 10, 15], key = 15
Output: 4
Explanation: The key is present at index '4' in the array.

Example 4:

1
2
3
Input: [1, 3, 8, 10, 15], key = 200
Output: -1
Explanation: The key is not present in the array.

Constraints:

  • 1 <= reader.length <= 10^4
  • -10^4 <= reader[i], target <= 10^4
  • reader is sorted in a strictly increasing order.

Solution

The problem follows the Binary Search pattern. Since Binary Search helps us find a number in a sorted array efficiently, we can use a modified version of the Binary Search to find the ‘key’ in an infinite sorted array.

The only issue with applying binary search in this problem is that we don’t know the bounds of the array. To handle this situation, we will first find the proper bounds of the array where we can perform a binary search.

An efficient way to find the proper bounds is to start at the beginning of the array with the bound’s size as ‘1’ and exponentially increase the bound’s size (i.e., double it) until we find the bounds that can have the key.

Consider Example-1 mentioned above:

Once we have searchable bounds we can apply the binary search.

Code

Here is what our algorithm will look like:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
import math


# class ArrayReader:

#   def __init__(self, arr):
#     self.arr = arr

#   def get(self, index):
#     if index >= len(self.arr):
#       return math.inf
#     return self.arr[index]


class Solution:
    def searchInfiniteSortedArray(self, reader, key):
        # find the proper bounds first
        start, end = 0, 1
        while reader.get(end) < key:
            newStart = end + 1
            end += (end - start + 1) * 2
            # increase to double the bounds size
            start = newStart

        return self.binary_search(reader, key, start, end)

    def binary_search(self, reader, key, start, end):
        while start <= end:
            mid = start + (end - start) // 2
            if key < reader.get(mid):
                end = mid - 1
            elif key > reader.get(mid):
                start = mid + 1
            else:  # found the key
                return mid

        return -1


def main():
    sol = Solution()
    reader = ArrayReader([4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30])
    print(sol.searchInfiniteSortedArray(reader, 16))
    print(sol.searchInfiniteSortedArray(reader, 11))
    reader = ArrayReader([1, 3, 8, 10, 15])
    print(sol.searchInfiniteSortedArray(reader, 15))
    print(sol.searchInfiniteSortedArray(reader, 200))


main()

Time complexity

There are two parts of the algorithm. In the first part, we keep increasing the bound’s size exponentially (double it every time) while searching for the proper bounds. Therefore, this step will take O(logN) assuming that the array will have maximum ‘N’ numbers. In the second step, we perform the binary search which will take O(logN), so the overall time complexity of our algorithm will be O(logN + logN) which is asymptotically equivalent to O(logN).

Space complexity

The algorithm runs in constant space O(1).

Minimum Difference Element (medium)

Design Gurus Educative.io

Problem Statement

Given an array of numbers sorted in ascending order, find the element in the array that has the minimum difference with the given ‘key’.

Example 1:

1
2
3
Input: [4, 6, 10], key = 7
Output: 6
Explanation: The difference between the key '7' and '6' is minimum than any other number in the array

Example 2:

1
2
Input: [4, 6, 10], key = 4
Output: 4

Example 3:

1
2
Input: [1, 3, 8, 10, 15], key = 12
Output: 10

Example 4:

1
2
Input: [4, 6, 10], key = 17
Output: 10

Solution

The problem follows the Binary Search pattern. Since Binary Search helps us find a number in a sorted array efficiently, we can use a modified version of the Binary Search to find the number that has the minimum difference with the given ‘key’.

We can use a similar approach as discussed in Order-agnostic Binary Search. We will try to search for the ‘key’ in the given array. If we find the ‘key’ we will return it as the minimum difference number. If we can’t find the ‘key’, (at the end of the loop) we can find the differences between the ‘key’ and the numbers pointed out by indices start and end, as these two numbers will be closest to the ‘key’. The number that gives minimum difference will be our required number.

Code

Here is what our algorithm will look like:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
class Solution:
    def searchMinDiffElement(self, arr, key):
        if key < arr[0]:
            return arr[0]
        n = len(arr)
        if key > arr[n - 1]:
            return arr[n - 1]

        start, end = 0, n - 1
        while start <= end:
            mid = start + (end - start) // 2
            if key < arr[mid]:
                end = mid - 1
            elif key > arr[mid]:
                start = mid + 1
            else:
                return arr[mid]

        # at the end of the while loop, 'start == end+1'
        # we are not able to find the element in the given array
        # return the element which is closest to the 'key'
        if (arr[start] - key) < (key - arr[end]):
            return arr[start]
        return arr[end]


def main():
    sol = Solution()
    print(sol.searchMinDiffElement([4, 6, 10], 7))
    print(sol.searchMinDiffElement([4, 6, 10], 4))
    print(sol.searchMinDiffElement([1, 3, 8, 10, 15], 12))
    print(sol.searchMinDiffElement([4, 6, 10], 17))


main()

Time complexity

Since, we are reducing the search range by half at every step, this means the time complexity of our algorithm will be O(logN) where ‘N’ is the total elements in the given array.

Space complexity

The algorithm runs in constant space O(1).

#Bitonic Array Maximum (easy)

852. Peak Index in a Mountain Array Design Gurus Educative.io

Problem Statement

Find the maximum value in a given Bitonic array. An array is considered bitonic if it is monotonically increasing and then monotonically decreasing. Monotonically increasing or decreasing means that for any index i in the array arr[i] != arr[i+1].

Example 1:

1
2
3
Input: [1, 3, 8, 12, 4, 2]
Output: 12
Explanation: The maximum number in the input bitonic array is '12'.

Example 2:

1
2
Input: [3, 8, 3, 1]
Output: 8

Example 3:

1
2
Input: [1, 3, 8, 12]
Output: 12

Example 4:

1
2
Input: [10, 9, 8]
Output: 10

Constraints:

  • 1 <= arr.length <= 10^5
  • -105 <= arr[i] <= 10^5

Solution

A bitonic array is a sorted array; the only difference is that its first part is sorted in ascending order and the second part is sorted in descending order. We can use a similar approach as discussed in Order-agnostic Binary Search. Since no two consecutive numbers are same (as the array is monotonically increasing or decreasing), whenever we calculate the middle, we can compare the numbers pointed out by the index middle and middle+1 to find if we are in the ascending or the descending part. So:

  1. If arr[middle] > arr[middle + 1], we are in the second (descending) part of the bitonic array. Therefore, our required number could either be pointed out by middle or will be before middle. This means we will be doing: end = middle.
  2. If arr[middle] <= arr[middle + 1], we are in the first (ascending) part of the bitonic array. Therefore, the required number will be after middle. This means we will be doing: start = middle + 1.

We can break when start == end. Due to the two points mentioned above, both start and end will be pointing at the maximum number of the bitonic array.

Code

Here is what our algorithm will look like:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution:
    def findMax(self, arr):
        start, end = 0, len(arr) - 1
        # 注意这里是<,而不是<=,不然会死循环
        while start < end:
            mid = start + (end - start) // 2
            if arr[mid] > arr[mid + 1]:
                end = mid
            else:
                start = mid + 1

        # at the end of the while loop, 'start == end'
        return arr[start]


def main():
    sol = Solution()
    print(sol.findMax([1, 3, 8, 12, 4, 2]))
    print(sol.findMax([3, 8, 3, 1]))
    print(sol.findMax([1, 3, 8, 12]))
    print(sol.findMax([10, 9, 8]))


main()

Time complexity

Since we are reducing the search range by half at every step, this means that the time complexity of our algorithm will be O(logN) where ‘N’ is the total elements in the given array.

Space complexity

The algorithm runs in constant space O(1).

Problem Challenge 1

Design Gurus Educative.io

Search Bitonic Array (medium)

Given a Bitonic array, find if a given ‘key’ is present in it. An array is considered bitonic if it is monotonically increasing and then monotonically decreasing. Monotonically increasing or decreasing means that for any index i in the array arr[i] != arr[i+1].

Write a function to return the index of the ‘key’. If the ‘key’ is not present, return -1.

Example 1:

1
2
Input: [1, 3, 8, 4, 3], key=4
Output: 3

Example 2:

1
2
Input: [3, 8, 3, 1], key=8
Output: 1

Example 3:

1
2
Input: [1, 3, 8, 12], key=12
Output: 3

Example 4:

1
2
Input: [10, 9, 8], key=10
Output: 0

Solution

The problem follows the Binary Search pattern. Since Binary Search helps us efficiently find a number in a sorted array we can use a modified version of the Binary Search to find the ‘key’ in the bitonic array.

Here is how we can search in a bitonic array:

  1. First, we can find the index of the maximum value of the bitonic array, similar to Bitonic Array Maximum. Let’s call the index of the maximum number maxIndex.
  2. Now, we can break the array into two sub-arrays:
    • Array from index ‘0’ to maxIndex, sorted in ascending order.
    • Array from index maxIndex+1 to array_length-1, sorted in descending order.
  3. We can then call Binary Search separately in these two arrays to search the ‘key’. We can use the same Order-agnostic Binary Search for searching.

Code

Here is what our algorithm will look like:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
class Solution:
    def search(self, arr, key):
        maxIndex = self.find_max(arr)
        keyIndex = self.binary_search(arr, key, 0, maxIndex)
        if keyIndex != -1:
            return keyIndex
        # max_index + 1 也可以，如果没有右边的区间，就会返回-1
        return self.binary_search(arr, key, maxIndex + 1, len(arr) - 1)

    # find index of the maximum value in a bitonic array
    def find_max(self, arr):
        start, end = 0, len(arr) - 1
        while start < end:
            mid = start + (end - start) // 2
            if arr[mid] > arr[mid + 1]:
                end = mid
            else:
                start = mid + 1

        # at the end of the while loop, 'start == end'
        return start

    # order-agnostic binary search
    def binary_search(self, arr, key, start, end):
        while start <= end:
            mid = int(start + (end - start) / 2)

            if key == arr[mid]:
                return mid

            if arr[start] < arr[end]:  # ascending order
                if key < arr[mid]:
                    end = mid - 1
                else:  # key > arr[mid]
                    start = mid + 1
            else:  # descending order
                if key > arr[mid]:
                    end = mid - 1
                else:  # key < arr[mid]
                    start = mid + 1

        return -1  # element is not found


def main():
    sol = Solution()
    print(sol.search([1, 3, 8, 4, 3], 4))
    print(sol.search([3, 8, 3, 1], 8))
    print(sol.search([1, 3, 8, 12], 12))
    print(sol.search([10, 9, 8], 10))


main()

Time complexity

Since we are reducing the search range by half at every step, this means that the time complexity of our algorithm will be O(logN) where ‘N’ is the total elements in the given array.

Space complexity

The algorithm runs in constant space O(1).

Problem Challenge 2

Top Interview 150 | 33. Search in Rotated Sorted Array Design Gurus Educative.io

Search in Rotated Array (medium)

Given an array of numbers which is sorted in ascending order and also rotated by some arbitrary number, find if a given ‘key’ is present in it.

Write a function to return the index of the ‘key’ in the rotated array. If the ‘key’ is not present, return -1. You can assume that the given array does not have any duplicates.

Example 1:

1
2
3
Input: [10, 15, 1, 3, 8], key = 15
Output: 1
Explanation: '15' is present in the array at index '1'.

Example 2:

1
2
3
Input: [4, 5, 7, 9, 10, -1, 2], key = 10
Output: 4
Explanation: '10' is present in the array at index '4'.

Constraints:

  • 1 <= arr.length <= 5000
  • -10^4 <= arr[i] <= 10^4
  • All values of nums are unique.
  • arr is an ascending array that is possibly rotated.
  • -10^4 <= key <= 10^4

Solution

The problem follows the Binary Search pattern. We can use a similar approach as discussed in Order-agnostic Binary Search and modify it similar to Search Bitonic Array to search for the ‘key’ in the rotated array.

After calculating the middle, we can compare the numbers at indices start and middle. This will give us two options:

  1. If arr[start] <= arr[middle], the numbers from start to middle are sorted in ascending order.
  2. Else, the numbers from middle+1 to end are sorted in ascending order.

Once we know which part of the array is sorted, it is easy to adjust our ranges. For example, if option-1 is true, we have two choices:

  1. By comparing the ‘key’ with the numbers at index start and middle we can easily find out if the ‘key’ lies between indices start and middle; if it does, we can skip the second part => end = middle -1.
  2. Else, we can skip the first part => start = middle + 1.

Let’s visually see this with the above-mentioned Example-2:

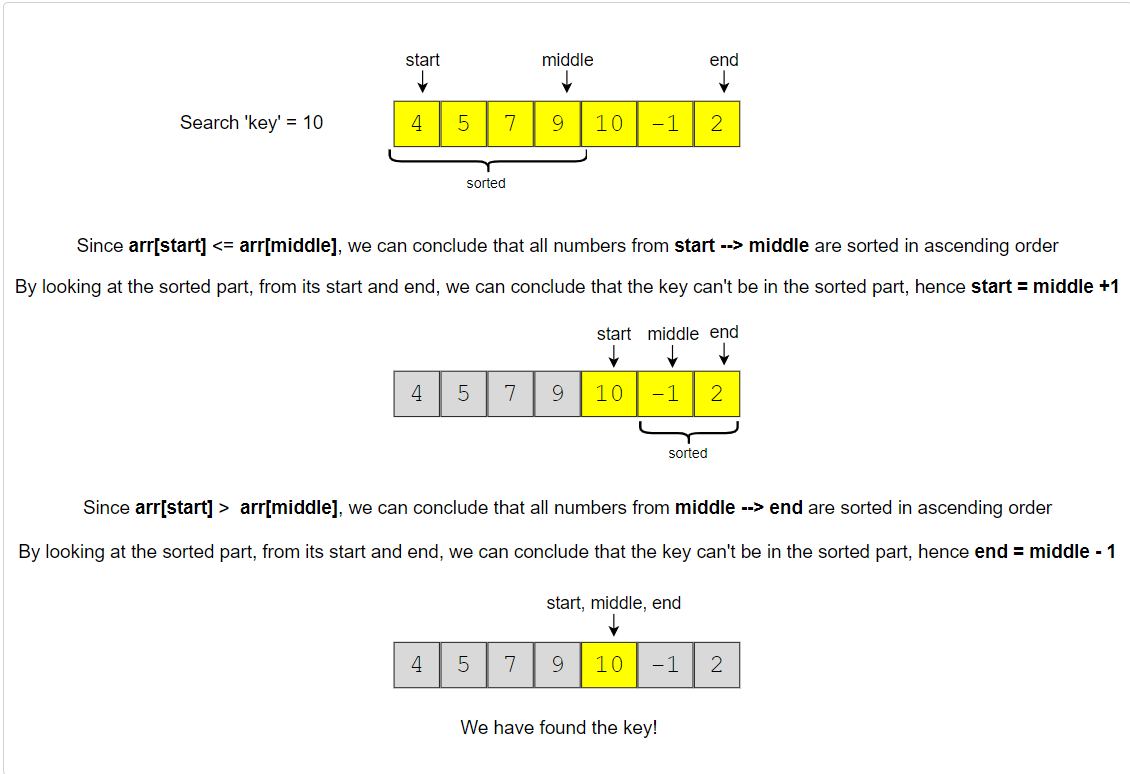
Since there are no duplicates in the given array, it is always easy to skip one part of the array in each iteration. However, if there are duplicates, it is not always possible to know which part is sorted. We will look into this case in the ‘Similar Problems’ section.

Code

Here is what our algorithm will look like:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution:
    def search(self, arr, key):
        start, end = 0, len(arr) - 1
        while start <= end:
            mid = start + (end - start) // 2
            if arr[mid] == key:
                return mid

            # 注意 虽然题目中说没有重复的数字，但是这里还是<= 不然这个用例失败：[3,1] key = 1
            if arr[start] <= arr[mid]:  # left side is sorted in ascending order
                if key >= arr[start] and key < arr[mid]:
                    end = mid - 1
                else:  # key > arr[mid]
                    start = mid + 1
            else:  # right side is sorted in ascending order
                if key > arr[mid] and key <= arr[end]:
                    start = mid + 1
                else:
                    end = mid - 1

        # we are not able to find the element in the given array
        return -1


def main():
    sol = Solution()
    print(sol.search([10, 15, 1, 3, 8], 15))
    print(sol.search([4, 5, 7, 9, 10, -1, 2], 10))


main()

Time complexity

Since we are reducing the search range by half at every step, this means that the time complexity of our algorithm will be O(logN) where ‘N’ is the total elements in the given array.

Space complexity

The algorithm runs in constant space O(1).

Similar Problems

Similar | 81. Search in Rotated Sorted Array II Design Gurus Educative.io

Problem 1

How do we search in a sorted and rotated array that also has duplicates?

The code above will fail in the following example!

Example 1:

1
2
3
Input: [3, 7, 3, 3, 3], key = 7
Output: 1
Explanation: '7' is present in the array at index '1'.

Solution

The only problematic scenario is when the numbers at indices start, middle, and end are the same, as in this case, we can’t decide which part of the array is sorted. In such a case, the best we can do is to skip one number from both ends: start = start + 1 & end = end - 1.

Code

The code is quite similar to the above solution. Only the highlighted lines have changed:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
class Solution:
    def search(self, arr, key):
        start, end = 0, len(arr) - 1
        while start <= end:
            mid = start + (end - start) // 2
            if arr[mid] == key:
                return mid

            # the only difference from the previous solution,
            # if numbers at indexes start, mid, and end are same, we can't choose a side
            # the best we can do, is to skip one number from both ends as key != arr[mid]
            if arr[start] == arr[mid] and arr[end] == arr[mid]:
                start += 1
                end -= 1
            elif arr[start] <= arr[mid]:  # left side is sorted in ascending order
                if key >= arr[start] and key < arr[mid]:
                    end = mid - 1
                else:  # key > arr[mid]
                    start = mid + 1

            else:  # right side is sorted in ascending order
                if key > arr[mid] and key <= arr[end]:
                    start = mid + 1
                else:
                    end = mid - 1

        # we are not able to find the element in the given array
        return -1


def main():
    sol = Solution()
    print(sol.search([3, 7, 3, 3, 3], 7))


main()

Time complexity

This algorithm will run most of the times in O(logN). However, since we only skip two numbers in case of duplicates instead of half of the numbers, the worst case time complexity will become O(N).

Space complexity

The algorithm runs in constant space O(1).

Problem Challenge 3

Top Interview 150 | 153. Find Minimum in Rotated Sorted Array Design Gurus Educative.io

Rotation Count (medium)

Given an array of numbers which is sorted in ascending order and is rotated ‘k’ times around a pivot, find ‘k’.

You can assume that the array does not have any duplicates.

Example 1:

1
2
3
Input: [10, 15, 1, 3, 8]
Output: 2
Explanation: The array has been rotated 2 times.

Example 2:

1
2
3
Input: [4, 5, 7, 9, 10, -1, 2]
Output: 5
Explanation: The array has been rotated 5 times.

Example 3:

1
2
3
Input: [1, 3, 8, 10]
Output: 0
Explanation: The array has been not been rotated.

Constraints:

  • 1 <= arr.length <= 5000
  • -10^4 <= arr[i] <= 10^4
  • All values of nums are unique.
  • arr is an ascending array that is possibly rotated.

Solution

This problem follows the Binary Search pattern. We can use a similar strategy as discussed in Search in Rotated Array.

In this problem, actually, we are asked to find the index of the minimum element. The number of times the minimum element is moved to the right will be equal to the number of rotations. An interesting fact about the minimum element is that it is the only element in the given array which is smaller than its previous element. Since the array is sorted in ascending order, all other elements are bigger than their previous element.

After calculating the middle, we can compare the number at index middle with its previous and next number. This will give us two options:

  1. If arr[middle] > arr[middle + 1], then the element at middle + 1 is the smallest.
  2. If arr[middle - 1] > arr[middle], then the element at middle is the smallest.

To adjust the ranges we can follow the same approach as discussed in Search in Rotated Array. Comparing the numbers at indices start and middle will give us two options:

  1. If arr[start] < arr[middle], the numbers from start to middle are sorted.
  2. Else, the numbers from middle + 1 to end are sorted.

Code

Here is what our algorithm will look like:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution:
    def countRotations(self, arr):
        start, end = 0, len(arr) - 1
        while start <= end:
            # while start < end: # code给的是<,但是上面的<=过了leetcode
            mid = start + (end - start) // 2

            # if mid is greater than the next element
            if mid < end and arr[mid] > arr[mid + 1]:
                return mid + 1

            # if mid is smaller than the previous element
            if mid > start and arr[mid - 1] > arr[mid]:
                return mid

            if arr[start] < arr[mid]:  # left side is sorted, so the pivot is on right side
                start = mid + 1
            else:  # right side is sorted, so the pivot is on the left side
                end = mid - 1

        return 0  # the array has not been rotated


def main():
    sol = Solution()
    print(sol.countRotations([10, 15, 1, 3, 8]))
    print(sol.countRotations([4, 5, 7, 9, 10, -1, 2]))
    print(sol.countRotations([1, 3, 8, 10]))


main()

Time complexity

Since we are reducing the search range by half at every step, this means that the time complexity of our algorithm will be O(logN) where ‘N’ is the total elements in the given array.

Space complexity

The algorithm runs in constant space O(1).

Similar Problems

没看懂leetcode的例子 | 154. Find Minimum in Rotated Sorted Array II Design Gurus Educative.io

Problem 1

How do we find the rotation count of a sorted and rotated array that has duplicates too?

The above code will fail on the following example!

Example 1:

1
2
3
Input: [3, 3, 7, 3]
Output: 3
Explanation: The array has been rotated 3 times

Solution
We can follow the same approach as discussed in Search in Rotated Array. The only difference is that before incrementing start or decrementing end, we will check if either of them is the smallest number.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
class Solution:
    def countRotations(self, arr):
        start, end = 0, len(arr) - 1
        while start < end:
            mid = start + (end - start) // 2
            # if element at mid is greater than the next element
            if mid < end and arr[mid] > arr[mid + 1]:
                return mid + 1
            # if element at mid is smaller than the previous element
            if mid > start and arr[mid - 1] > arr[mid]:
                return mid

            # this is the only difference from the previous solution
            # if numbers at indices start, mid, and end are same, we can't choose a side
            # the best we can do is to skip one number from both ends if they are not the
            # smallest number
            if arr[start] == arr[mid] and arr[end] == arr[mid]:
                if arr[start] > arr[start + 1]:  # if element at start+1 is not the smallest
                    return start + 1
                start += 1
                if arr[end - 1] > arr[end]:  # if the element at end is not the smallest
                    return end
                end -= 1
            # left side is sorted, so the pivot is on right side
            elif arr[start] < arr[mid] or (arr[start] == arr[mid] and arr[mid] > arr[end]):
                start = mid + 1
            else:  # right side is sorted, so the pivot is on the left side
                end = mid - 1

        return 0  # the array has not been rotated


def main():
    sol = Solution()
    print(sol.countRotations([3, 3, 7, 3]))


main()

Time complexity

This algorithm will run in O(logN) most of the times, but since we only skip two numbers in case of duplicates instead of the half of the numbers, therefore the worst case time complexity will become O(N).

Space complexity

The algorithm runs in constant space O(1).

Author：Hasuer

Link：https://hasuer.github.io/16-pattern-modified-binary-search/index.html

Publish date：May 16th 2024, 3:26:29 pm

Update date：May 28th 2024, 11:29:25 am

License：本文采用知识共享署名-非商业性使用 4.0 国际许可协议进行许可

CATALOG
  1. 1. Introduction
  2. 2. Order-agnostic Binary Search (easy)
    1. 2.1. Problem Statement
    2. 2.2. Solution
    3. 2.3. Code
      1. 2.3.1. Time complexity
      2. 2.3.2. Space complexity
  3. 3. Ceiling of a Number (medium)
    1. 3.1. Problem Statement
    2. 3.2. Solution
    3. 3.3. Code
      1. 3.3.1. Time complexity
      2. 3.3.2. Space complexity
    4. 3.4. Similar Problems
      1. 3.4.1. Problem 1
      2. 3.4.2. Code
  4. 4. Next Letter (medium)
    1. 4.1. Problem Statement
    2. 4.2. Solution
    3. 4.3. Code
      1. 4.3.1. Time complexity
      2. 4.3.2. Space complexity
  5. 5. #Number Range (medium)
    1. 5.1. Problem Statement
    2. 5.2. Solution
    3. 5.3. Code
      1. 5.3.1. Time complexity
      2. 5.3.2. Space complexity
  6. 6. #Search in a Sorted Infinite Array (medium)
    1. 6.1. Problem Statement
    2. 6.2. Solution
    3. 6.3. Code
      1. 6.3.1. Time complexity
      2. 6.3.2. Space complexity
  7. 7. Minimum Difference Element (medium)
    1. 7.1. Problem Statement
    2. 7.2. Solution
    3. 7.3. Code
      1. 7.3.1. Time complexity
      2. 7.3.2. Space complexity
  8. 8. #Bitonic Array Maximum (easy)
    1. 8.1. Problem Statement
    2. 8.2. Solution
    3. 8.3. Code
      1. 8.3.1. Time complexity
      2. 8.3.2. Space complexity
  9. 9. Problem Challenge 1
    1. 9.1. Search Bitonic Array (medium)
    2. 9.2. Solution
    3. 9.3. Code
      1. 9.3.1. Time complexity
      2. 9.3.2. Space complexity
  10. 10. Problem Challenge 2
    1. 10.1. Search in Rotated Array (medium)
    2. 10.2. Solution
    3. 10.3. Code
      1. 10.3.1. Time complexity
      2. 10.3.2. Space complexity
    4. 10.4. Similar Problems
      1. 10.4.1. Problem 1
      2. 10.4.2. Solution
      3. 10.4.3. Code
      4. 10.4.4. Time complexity
      5. 10.4.5. Space complexity
  11. 11. Problem Challenge 3
    1. 11.1. Rotation Count (medium)
    2. 11.2. Solution
    3. 11.3. Code
      1. 11.3.1. Time complexity
      2. 11.3.2. Space complexity
    4. 11.4. Similar Problems
      1. 11.4.1. Problem 1
      2. 11.4.2. Time complexity
      3. 11.4.3. Space complexity
Total : 41
2024
2022
2021
Interview
技术笔记 Grokking-Interview-Pattern