19. Pattern K-way merge

Grokking Interview Pattern Interview

Word count: 4.2kReading time: 25 min

 2024/05/19 

Introduction

This pattern helps us solve problems that involve a list of sorted arrays.

Whenever we are given ‘K’ sorted arrays, we can use a Heap to efficiently perform a sorted traversal of all the elements of all arrays. We can push the smallest (first) element of each sorted array in a Min Heap to get the overall minimum. While inserting elements to the Min Heap we keep track of which array the element came from. We can, then, remove the top element from the heap to get the smallest element and push the next element from the same array, to which this smallest element belonged, to the heap. We can repeat this process to make a sorted traversal of all elements.

Let’s see this pattern in action.

Merge K Sorted Lists (medium)

Top Interview 150 | 23. Merge k Sorted Lists Design Gurus Educative.io

Problem Statemen

Given an array of ‘K’ sorted LinkedLists, merge them into one sorted list.

Example 1:

1 2	Input: L1=[2, 6, 8], L2=[3, 6, 7], L3=[1, 3, 4] Output: [1, 2, 3, 3, 4, 6, 6, 7, 8]

Example 2:

1 2	Input: L1=[5, 8, 9], L2=[1, 7] Output: [1, 5, 7, 8, 9]

Constraints:

k == lists.length
0 <= k <= 10^4
0 <= lists[i].length <= 500
-10^4 <= lists[i][j] <= 10^4
lists[i] is sorted in ascending order.
The sum of lists[i].length will not exceed 10^4.

Solution

A brute force solution could be to add all elements of the given ‘K’ lists to one list and sort it. If there are a total of ‘N’ elements in all the input lists, then the brute force solution will have a time complexity of O(NlogN) as we will need to sort the merged list. Can we do better than this? How can we utilize the fact that the input lists are individually sorted?

If we have to find the smallest element of all the input lists, we have to compare only the smallest (i.e. the first) element of all the lists. Once we have the smallest element, we can put it in the merged list. Following a similar pattern, we can then find the next smallest element of all the lists to add it to the merged list.

The best data structure that comes to mind to find the smallest number among a set of ‘K’ numbers is a Heap). Let’s see how can we use a heap to find a better algorithm.

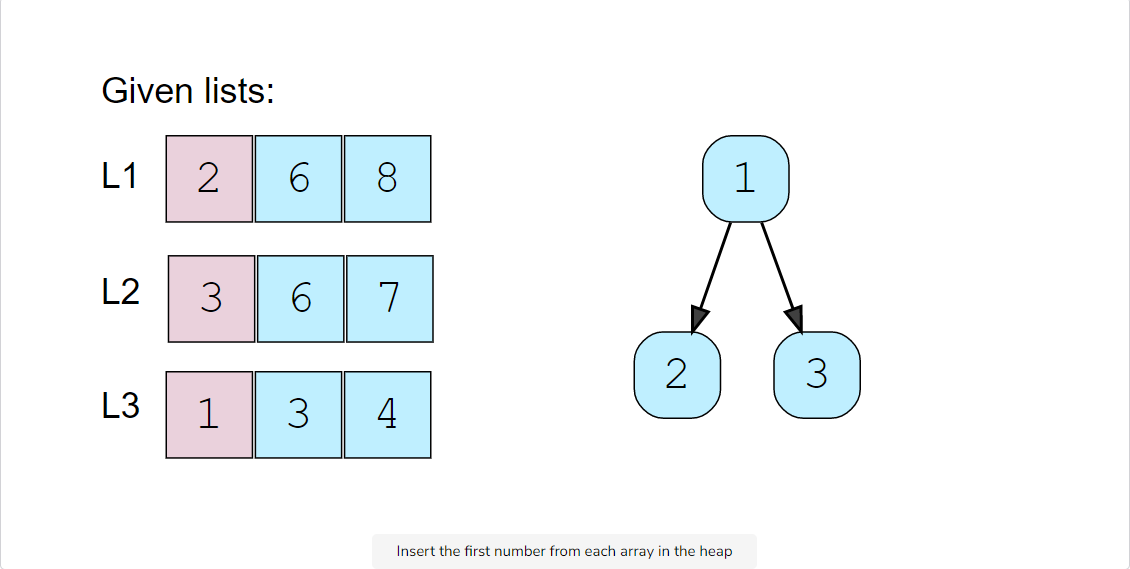
We can insert the first element of each array in a Min Heap.
After this, we can take out the smallest (top) element from the heap and add it to the merged list.
After removing the smallest element from the heap, we can insert the next element of the same list into the heap.
We can repeat steps 2 and 3 to populate the merged list in sorted order.

Let’s take the Example-1 mentioned above to go through each step of our algorithm:

Given lists: L1=[2, 6, 8], L2=[3, 6, 7],L3=[1, 3, 4]

After inserting the 1st element of each list, the heap will have the following elements:
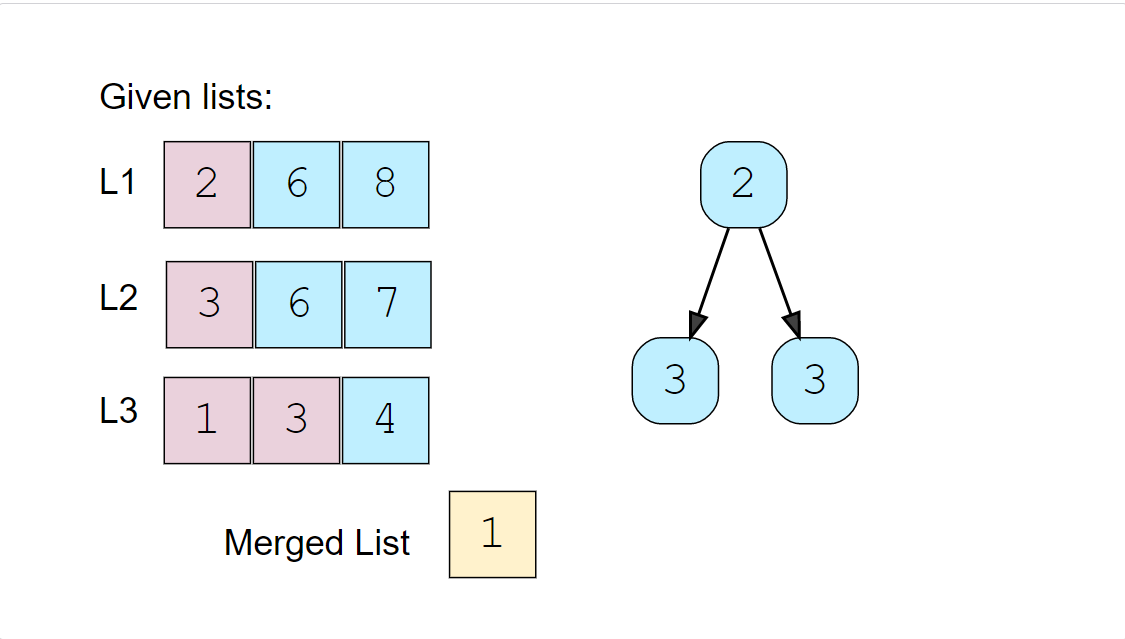
We’ll take the top number from the heap, insert it into the merged list and add the next number in the heap.
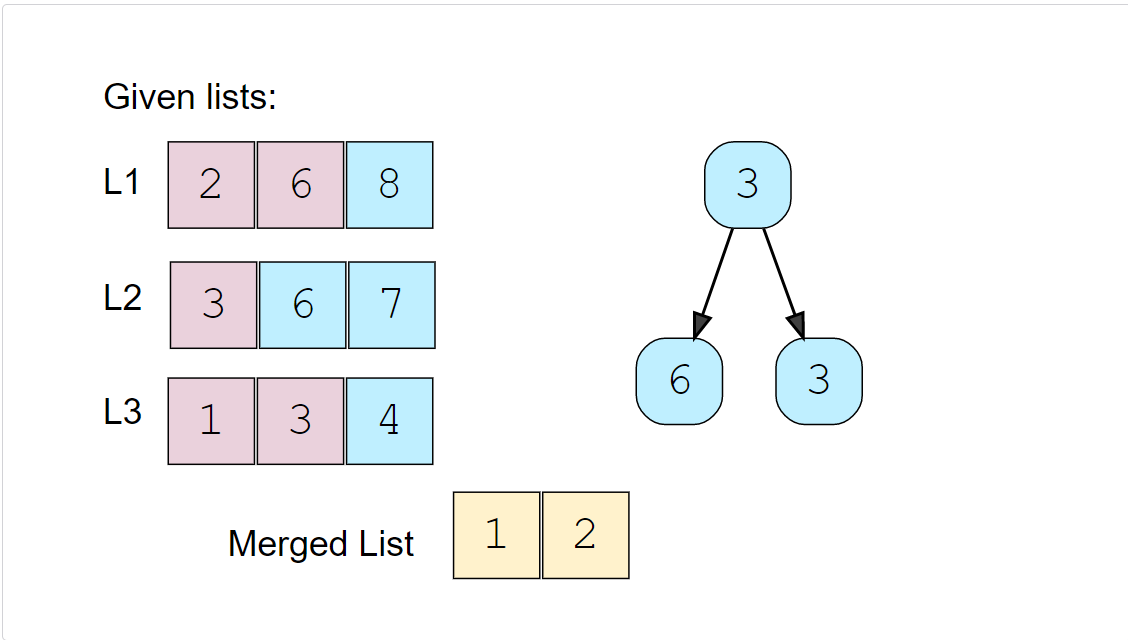
Again, we’ll take the top element of the heap, insert it into the merged list and add the next number to the heap.
Repeating the above step, take the top element of the heap, insert it into the merged list and add the next number to the heap. As there are two 3s in the heap, we can pick anyone but we need to take the next element from the corresponding list to insert in the heap.

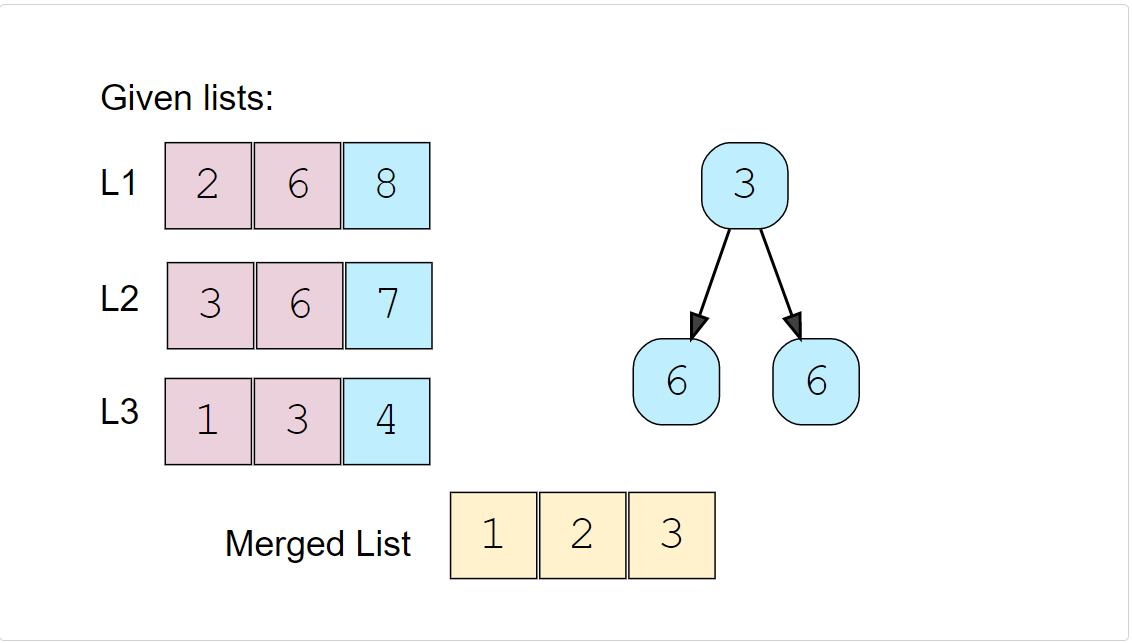
We’ll repeat the above step to populate our merged array.

Code

Here is what our algorithm will look like:

from heapq import *


# class Node:
#   def __init__(self, val):
#     self.val = val
#     self.next = None

#   # used for the min-heap
#   def __lt__(self, other):
#     return self.val < other.val


class Solution:
  def merge(self, lists):
    minHeap = []

    # put the root of each list in the min heap
    for root in lists:
      if root is not None:
        # 这里pycharm可以自动根据root的值排序，但是leetcode不行，所以这种写法不能过leetcode
        heappush(minHeap, root)

    # take the smallest(top) element form the min-heap and add it to the result
    # if the top element has a next element add it to the heap
    resultHead, resultTail = None, None
    while minHeap:
      node = heappop(minHeap)
      if resultHead is None:
        resultHead = resultTail = node
      else:
        resultTail.next = node
        resultTail = resultTail.next

      if node.next is not None:
        heappush(minHeap, node.next)

    return resultHead


def main():
  sol = Solution()
  l1 = Node(2)
  l1.next = Node(6)
  l1.next.next = Node(8)

  l2 = Node(3)
  l2.next = Node(6)
  l2.next.next = Node(7)

  l3 = Node(1)
  l3.next = Node(3)
  l3.next.next = Node(4)

  result = sol.merge([l1, l2, l3])
  print("Here are the elements form the merged list: ", end='')
  while result is not None:
    print(str(result.val) + " ", end='')
    result = result.next


main()


#=====================================leetcode==========================================
from heapq import *


class ListNode:
    def __init__(self, value):
        self.value = value
        self.next = None

    def __lt__(self, other):
        return self.value < other.value


def merge_lists(lists):
    min_heap = []
    
    # put the root of each list in the min heap
    for root in lists:
        if root:
            heappush(min_heap, (root.value, root))

    # take the smallest(top)element form the min-heap and add it to the result
    # if the top element has a next element add it to the heap
    result_head, result_tail = None, None
    while min_heap:
        node = heappop(min_heap)[1]
        if result_head is None:
            result_head = result_tail = node
        else:
            result_tail.next = node
            result_tail = result_tail.next
        if node.next:
            heappush(min_heap, (node.next.value, node.next))
    return result_head


def main():
    l1 = ListNode(1)
    l1.next = ListNode(4)
    l1.next.next = ListNode(5)

    l2 = ListNode(1)
    l2.next = ListNode(3)
    l2.next.next = ListNode(4)

    l3 = ListNode(2)
    l3.next = ListNode(6)

    result = merge_lists([l1, l2, l3])
    while result:
        print(str(result.value), end=" ")
        result = result.next


if __name__ == '__main__':
    main()

Time complexity

Since we’ll be going through all the elements of all arrays and will be removing/adding one element to the heap in each step, the time complexity of the above algorithm will be O(N\logK)*, where ‘N’ is the total number of elements in all the ‘K’ input arrays.

Space complexity

The space complexity will be O(K) because, at any time, our min-heap will be storing one number from all the ‘K’ input arrays.

Kth Smallest Number in M Sorted Lists (Medium)

Similar | 378. Kth Smallest Element in a Sorted Matrix Design Gurus Educative.io

Problem Statement

Given ‘M’ sorted arrays, find the K’th smallest number among all the arrays.

Example 1:

Input: L1=[2, 6, 8], L2=[3, 6, 7], L3=[1, 3, 4], K=5
Output: 4
Explanation: The 5th smallest number among all the arrays is 4, this can be verified from the merged 
list of all the arrays: [1, 2, 3, 3, 4, 6, 6, 7, 8]

Example 2:

1
2
3

Input: L1=[5, 8, 9], L2=[1, 7], K=3
Output: 7
Explanation: The 3rd smallest number among all the arrays is 7.

Solution

This problem follows the K-way merge pattern and we can follow a similar approach as discussed in Merge K Sorted Lists.

We can start merging all the arrays, but instead of inserting numbers into a merged list, we will keep count to see how many elements have been inserted in the merged list. Once that count is equal to ‘K’, we have found our required number.

A big difference from Merge K Sorted Lists is that in this problem, the input is a list of arrays compared to LinkedLists. This means that when we want to push the next number in the heap we need to know what the index of the current number in the current array was. To handle this, we will need to keep track of the array and the element indices.

Code

Here is what our algorithm will look like:

from heapq import *


class Solution:
    def findKthSmallest(self, lists, k):
        # 注意，这里和之前不一样，这里应该使用的是minheap,如果还是max_heap，那就相当于每个数组都要全部遍历，这样的时间复杂度会上去
        minHeap = []

        # put the 1st element of each list in the min heap
        for i in range(len(lists)):
            heappush(minHeap, (lists[i][0], 0, lists[i]))

        # take the smallest(top) element form the min heap, if the running count is equal to k
        # return the number
        numberCount, number = 0, 0
        while minHeap:
            number, i, list = heappop(minHeap)
            numberCount += 1
            if numberCount == k:
                # 当然，这里也可以直接return num,在while循环外面的return num改成return 0也可以（参考上面我的写法）
                break
            # if the array of the top element has more elements, add the next element to the heap
            if len(list) > i + 1:
                heappush(minHeap, (list[i + 1], i + 1, list))

        return number


def main():
    sol = Solution()
    print("Kth smallest number is: " +
          str(sol.findKthSmallest([[2, 6, 8], [3, 6, 7], [1, 3, 4]], 5)))


main()

================================leetcode=================================
# 这个也能过leetcode
from heapq import *


def find_kth_smallest(lists, k):
    # 注意，这里和之前不一样，这里应该使用的是minheap,如果还是max_heap，那就相当于每个数组都要全部遍历，这样的时间复杂度会上去
    min_heap = []
    for i in range(len(lists)):
        heappush(min_heap, (lists[i][0], i, 0))

    while min_heap and k:
        num, list_index, index = heappop(min_heap)
        k -= 1
        if k == 0:
            return num
        if index != len(lists[list_index]) - 1:
            heappush(min_heap, (lists[list_index][index + 1], list_index, index + 1))
    return 0


def main():
    res = find_kth_smallest([[2, 6, 8], [3, 6, 7], [1, 3, 4]], 5)
    print(str(res))
    res = find_kth_smallest([[5, 8, 9], [1, 7]], 3)
    print(str(res))


if __name__ == '__main__':
    main()

Time complexity

Since we’ll be going through at most ‘K’ elements among all the arrays, and we will remove/add one element in the heap in each step, the time complexity of the above algorithm will be O(KlogM)O(K∗log*M) where ‘M’ is the total number of input arrays.

Space complexity

The space complexity will be O(M)O(M) because, at any time, our min-heap will be storing one number from all the ‘M’ input arrays.

#Kth Smallest Number in a Sorted Matrix (Hard)

378. Kth Smallest Element in a Sorted Matrix Design Gurus Educative.io

Problem Statement

Given an N\ N matrix where *each row and column is sorted in ascending order, find the Kth smallest element in the matrix.

Example 1:

Input: Matrix=[
    [2, 6, 8], 
    [3, 7, 10],
    [5, 8, 11]
  ], 
  K=5
Output: 7
Explanation: The 5th smallest number in the matrix is 7.

Constraints:

n == matrix.length == matrix[i].length
1 <= n <= 300
-10^9 <= matrix[i][j] <= 10^9
All the rows and columns of matrix are guaranteed to be sorted in non-decreasing order.
1 <= k <= n^2

Solution

This problem follows the K-way merge pattern and can be easily converted to Kth Smallest Number in M Sorted Lists. As each row (or column) of the given matrix can be seen as a sorted list, we essentially need to find the Kth smallest number in ‘N’ sorted lists.

Code

Here is what our algorithm will look like:

# 和上面一道题一摸一样
from heapq import *

class Solution:
  def findKthSmallest(self, matrix, k):
      minHeap = []

      # put the 1st element of each row in the min heap
      # we don't need to push more than 'k' elements in the heap
      for i in range(min(k, len(matrix))):
          heappush(minHeap, (matrix[i][0], 0, matrix[i]))

      # take the smallest(top) element form the min heap, if the running count is equal to
      # 'k' return the number. If the row of the top element has more elements, add the 
      # next element to the heap
      numberCount, number = 0, 0
      while minHeap:
          number, i, row = heappop(minHeap)
          numberCount += 1
          if numberCount == k:
              break
          if len(row) > i+1:
              heappush(minHeap, (row[i+1], i+1, row))
      return number


def main():
  sol = Solution()
  print("Kth smallest number is: " +
        str(sol.findKthSmallest([[2, 6, 8], [3, 7, 10], [5, 8, 11]], 5)))


main()

Time complexity

First, we inserted at most ‘K’ or one element from each of the ‘N’ rows, which will take O(min(K, N)). Then we went through at most ‘K’ elements in the matrix and remove/add one element in the heap in each step. As we can’t have more than ‘N’ elements in the heap in any condition, therefore, the overall time complexity of the above algorithm will be O(min(K, N) + K\logN)*.

Space complexity

The space complexity will be O(N) because, in the worst case, our min-heap will be storing one number from each of the ‘N’ rows.

An Alternate Solution

Since each row and column of the matrix is sorted, is it possible to use Binary Search to find the Kth smallest number?

The biggest problem to use Binary Search, in this case, is that we don’t have a straightforward sorted array, instead, we have a matrix. As we remember, in Binary Search, we calculate the middle index of the search space (‘1’ to ‘N’) and see if our required number is pointed out by the middle index; if not we either search in the lower half or the upper half. In a sorted matrix, we can’t really find a middle. Even if we do consider some index as middle, it is not straightforward to find the search space containing numbers bigger or smaller than the number pointed out by the middle index.

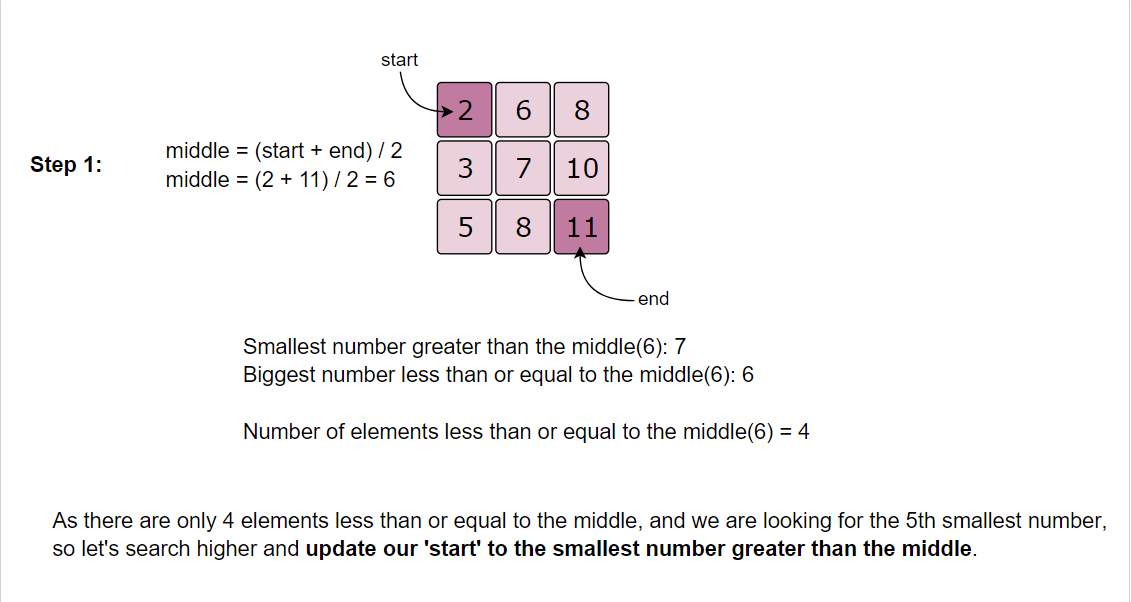
An alternative could be to apply the Binary Search on the “number range” instead of the “index range”. As we know that the smallest number of our matrix is at the top left corner and the biggest number is at the bottom right corner. These two numbers can represent the “range” i.e., the start and the end for the Binary Search. Here is how our algorithm will work:

Start the Binary Search with start = matrix[0][0] and end = matrix[n-1][n-1].
Find middle of the start and the end. This middle number is NOT necessarily an element in the matrix.
Count all the numbers smaller than or equal to middle in the matrix. As the matrix is sorted, we can do this in O(N).
While counting, we can keep track of the “smallest number greater than the middle” (let’s call it n1) and at the same time the “biggest number less than or equal to the middle” (let’s call it n2). These two numbers will be used to adjust the “number range” for the Binary Search in the next iteration.
If the count is equal to ‘K’, n1 will be our required number as it is the “biggest number less than or equal to the middle”, and is definitely present in the matrix.
If the count is less than ‘K’, we can update start = n2 to search in the higher part of the matrix and if the count is greater than ‘K’, we can update end = n1 to search in the lower part of the matrix in the next iteration.

Here is the visual representation of our algorithm:

Here is what our algorithm will look like:

class Solution:
  def findKthSmallest(self, matrix, k):
    n = len(matrix)
    start, end = matrix[0][0], matrix[n - 1][n - 1]
    while start < end:
      mid = start + (end - start) / 2
      smaller, larger = (matrix[0][0], matrix[n - 1][n - 1])

      count, smaller, larger = self.count_less_equal(matrix, mid, smaller, larger)

      if count == k:
        return smaller
      if count < k:
        start = larger  # search higher
      else:
        end = smaller  # search lower

    return start
  

  def count_less_equal(self, matrix, mid, smaller, larger):
    count, n = 0, len(matrix)
    row, col = n - 1, 0
    while row >= 0 and col < n:
      if matrix[row][col] > mid:
        # as matrix[row][col] is bigger than the mid, let's keep track of the
        # smallest number greater than the mid
        larger = min(larger, matrix[row][col])
        row -= 1
      else:
        # as matrix[row][col] is less than or equal to the mid, let's keep track of the
        # biggest number less than or equal to the mid
        smaller = max(smaller, matrix[row][col])
        count += row + 1
        col += 1

    return count, smaller, larger


def main():
  sol = Solution()
  print("Kth smallest number is: " +
        str(sol.findKthSmallest([[1, 4], [2, 5]], 2)))

  print("Kth smallest number is: " +
        str(sol.findKthSmallest([[-5]], 1)))

  print("Kth smallest number is: " +
        str(sol.findKthSmallest([[2, 6, 8], [3, 7, 10], [5, 8, 11]], 5)))

  print("Kth smallest number is: " +
        str(sol.findKthSmallest([[1, 5, 9], [10, 11, 13], [12, 13, 15]], 8)))


main()

Time complexity

The Binary Search could take O(log(max-min )) iterations where ‘max’ is the largest and ‘min’ is the smallest element in the matrix and in each iteration we take O(N) for counting, therefore, the overall time complexity of the algorithm will be O(N\log(max-min))*.

Space complexity

The algorithm runs in constant space O(1).

Smallest Number Range (Hard)

632. Smallest Range Covering Elements from K Lists Design Gurus Educative.io

Problem Statement

Given ‘M’ sorted arrays, find the smallest range that includes at least one number from each of the ‘M’ lists.

Example 1:

1
2
3

Input: L1=[1, 5, 8], L2=[4, 12], L3=[7, 8, 10]
Output: [4, 7]
Explanation: The range [4, 7] includes 5 from L1, 4 from L2 and 7 from L3.

Example 2:

1
2
3

Input: L1=[1, 9], L2=[4, 12], L3=[7, 10, 16]
Output: [9, 12]
Explanation: The range [9, 12] includes 9 from L1, 12 from L2 and 10 from L3.

Solution

This problem follows the K-way merge pattern and we can follow a similar approach as discussed in Merge K Sorted Lists.

We can start by inserting the first number from all the arrays in a min-heap. We will keep track of the largest number that we have inserted in the heap (let’s call it currentMaxNumber).

In a loop, we’ll take the smallest (top) element from the min-heap andcurrentMaxNumber has the largest element that we inserted in the heap. If these two numbers give us a smaller range, we’ll update our range. Finally, if the array of the top element has more elements, we’ll insert the next element to the heap.

We can finish searching the minimum range as soon as an array is completed or, in other terms, the heap has less than ‘M’ elements.

Code

Here is what our algorithm will look like:

from heapq import *
import math


class Solution:
    def findSmallestRange(self, lists):
        minHeap = []
        rangeStart, rangeEnd = 0, math.inf
        currentMaxNumber = -math.inf

        # put the 1st element of each array in the max heap
        for arr in lists:
            heappush(minHeap, (arr[0], 0, arr))
            currentMaxNumber = max(currentMaxNumber, arr[0])

        # take the smallest(top) element form the min heap, if it gives us smaller range,
        # update the ranges, if the array of the top element has more elements, insert the
        # next element in the heap
        # 思路一样，但是当时没有想到这个while循环的条件
        while len(minHeap) == len(lists):
            num, i, arr = heappop(minHeap)
            if rangeEnd - rangeStart > currentMaxNumber - num:
                rangeStart = num
                rangeEnd = currentMaxNumber

            if len(arr) > i + 1:
                # insert the next element in the heap
                heappush(minHeap, (arr[i + 1], i + 1, arr))
                currentMaxNumber = max(currentMaxNumber, arr[i + 1])

        return [rangeStart, rangeEnd]


def main():
    sol = Solution()
    print("Smallest range is: " +
          str(sol.findSmallestRange([[1, 5, 8], [4, 12], [7, 8, 10]])))


main()

Time complexity

Since, at most, we’ll be going through all the elements of all the arrays and will remove/add one element in the heap in each step, the time complexity of the above algorithm will be O(N\logM)* where ‘N’ is the total number of elements in all the ‘M’ input arrays.

Space complexity

The space complexity will be O(M) because, at any time, our min-heap will be store one number from all the ‘M’ input arrays.

Problem Challenge 1

Similar | Top Interview 150 | 373. Find K Pairs with Smallest Sums Design Gurus Educative.io

K Pairs with Largest Sums (Hard)

Given two sorted arrays in descending order, find ‘K’ pairs with the largest sum where each pair consists of numbers from both the arrays.

Example 1:

1
2
3

Input: L1=[9, 8, 2], L2=[6, 3, 1], K=3
Output: [9, 3], [9, 6], [8, 6] 
Explanation: These 3 pairs have the largest sum. No other pair has a sum larger than any of these.

Example 2:

1 2	Input: L1=[5, 2, 1], L2=[2, -1], K=3 Output: [5, 2], [5, -1], [2, 2]

Constraints:

1 <= nums1.length, nums2.length <= 10^5
-10^9 <= nums1[i], nums2[i] <= 10^9
nums1 and nums2 both are sorted in non-decreasing order.
1 <= k <= 10^4
k <= nums1.length * nums2.length

Solution

This problem follows the K-way merge pattern and we can follow a similar approach as discussed in Merge K Sorted Lists.

We can go through all the numbers of the two input arrays to create pairs and initially insert them all in the heap until we have ‘K’ pairs in Min Heap. After that, if a pair is bigger than the top (smallest) pair in the heap, we can remove the smallest pair and insert this pair in the heap.

We can optimize our algorithms in two ways:

Instead of iterating over all the numbers of both arrays, we can iterate only the first ‘K’ numbers from both arrays. Since the arrays are sorted in descending order, the pairs with the maximum sum will be constituted by the first ‘K’ numbers from both the arrays.
As soon as we encounter a pair with a sum that is smaller than the smallest (top) element of the heap, we don’t need to process the next elements of the array. Since the arrays are sorted in descending order, we won’t be able to find a pair with a higher sum moving forward.

Code

Here is what our algorithm will look like:

from heapq import *

class Solution:
  def findKLargestPairs(self, nums1, nums2, k):
    minHeap = []
    for i in range(0, min(k, len(nums1))):
      for j in range(min(k, len(nums2))):
        if len(minHeap) < k:
          heappush(minHeap, (nums1[i] + nums2[j], i, j))
        else:
          # if the sum of the two numbers from the two arrays is smaller than the 
          # smallest(top) element of the heap, we can 'break' here. Since the arrays are 
          # sorted in the descending order, we'll not be able to find a pair with a higher 
          # sum moving forward
          if nums1[i] + nums2[j] < minHeap[0][0]:
            break
          else: # we've a pair with a larger sum, remove top and insert this pair in heap
            heappop(minHeap)
            heappush(minHeap, (nums1[i] + nums2[j], i, j))

    result = []
    for (num, i, j) in minHeap:
      result.append([nums1[i], nums2[j]])

    return result


def main():
  sol = Solution()
  print("Pairs with largest sum are: " +
        str(sol.findKLargestPairs([9, 8, 2], [6, 3, 1], 3)))


main()

Time Complexity

Since, at most, we’ll be going through all the elements of both arrays and we will add/remove one element in the heap in each step, the time complexity of the above algorithm will be O(NMlogK) where ‘N’ and ‘M’ are the total number of elements in both arrays, respectively.

If we assume that both arrays have at least ‘K’ elements then the time complexity can be simplified to O(K^2logK), because we are not iterating more than ‘K’ elements in both arrays.

Space Complexity

The space complexity will be O(K) because, at any time, our Min Heap will be storing ‘K’ largest pairs.

Author：Hasuer

Link：https://hasuer.github.io/19-pattern-k-way-merge/index.html

Publish date：May 19th 2024, 5:40:47 pm

Update date：May 28th 2024, 11:29:55 am

License：本文采用知识共享署名-非商业性使用 4.0 国际许可协议进行许可

Next Post

20. Pattern Greedy Algorithms
Previous Post

18. Pattern Top 'K' Elements

CATALOG

19. Pattern K-way merge

Introduction

Merge K Sorted Lists (medium)

Problem Statemen

Solution

Code

Time complexity

Space complexity

Kth Smallest Number in M Sorted Lists (Medium)

Problem Statement

Solution

Code

Time complexity

Space complexity

Similar Problems

#Kth Smallest Number in a Sorted Matrix (Hard)

Problem Statement

Solution

Code

Time complexity

Space complexity

An Alternate Solution

Time complexity

Space complexity

Smallest Number Range (Hard)

Problem Statement

Solution

Code

Time complexity

Space complexity

Problem Challenge 1

K Pairs with Largest Sums (Hard)

Solution

Code

Time Complexity

Space Complexity