Hasuer's Studio.

14. Pattern Two Heaps

Grokking Interview Pattern Interview
Word count: 3.5kReading time: 21 min
2024/05/14

Introduction

In many problems, where we are given a set of elements such that we can divide them into two parts. To solve the problem, we are interested in knowing the smallest element in one part and the biggest element in the other part. This pattern is an efficient approach to solve such problems.

This pattern uses two Heaps to solve these problems; A Min Heap to find the smallest element and a Max Heap to find the biggest element.

Let’s jump onto our first problem to see this pattern in action.

Find the Median of a Number Stream (medium)

Top Interview 150 | 295. Find Median from Data Stream Design Gurus Educative.io

Introduction

Problem Statement

Design a class to calculate the median of a number stream. The class should have the following two methods:

  1. insertNum(int num): stores the number in the class
  2. findMedian(): returns the median of all numbers inserted in the class

If the count of numbers inserted in the class is even, the median will be the average of the middle two numbers.

Example 1:

1
2
3
4
5
6
7
1. insertNum(3)
2. insertNum(1)
3. findMedian() -> output: 2
4. insertNum(5)
5. findMedian() -> output: 3
6. insertNum(4)
7. findMedian() -> output: 3.5

Constraints:

  • -10^5 <= num <= 10^5
  • There will be at least one element in the data structure before calling findMedian.
  • At most 5 * 10^4 calls will be made to insertNum and findMedian.

Solution

As we know, the median is the middle value in an ordered integer list. So a brute force solution could be to maintain a sorted list of all numbers inserted in the class so that we can efficiently return the median whenever required. Inserting a number in a sorted list will take O(N) time if there are ‘N’ numbers in the list. This insertion will be similar to the Insertion sort. Can we do better than this? Can we utilize the fact that we don’t need the fully sorted list - we are only interested in finding the middle element?

Assume ‘x’ is the median of a list. This means that half of the numbers in the list will be smaller than (or equal to) ‘x’ and half will be greater than (or equal to) ‘x’. This leads us to an approach where we can divide the list into two halves: one half to store all the smaller numbers (let’s call it smallNumList) and one half to store the larger numbers (let’s call it largNumList). The median of all the numbers will either be the largest number in the smallNumList or the smallest number in the largNumList. If the total number of elements is even, the median will be the average of these two numbers.

The best data structure that comes to mind to find the smallest or largest number among a list of numbers is a Heap). Let’s see how we can use a heap to find a better algorithm.

  1. We can store the first half of numbers (i.e., smallNumList) in a Max Heap. We should use a Max Heap as we are interested in knowing the largest number in the first half.
  2. We can store the second half of numbers (i.e., largeNumList) in a Min Heap, as we are interested in knowing the smallest number in the second half.
  3. Inserting a number in a heap will take O(logN), which is better than the brute force approach.
  4. At any time, the median of the current list of numbers can be calculated from the top element of the two heaps.

Let’s take the Example-1 mentioned above to go through each step of our algorithm:

  1. insertNum(3): We can insert a number in the Max Heap (i.e. first half) if the number is smaller than the top (largest) number of the heap. After every insertion, we will balance the number of elements in both heaps, so that they have an equal number of elements. If the count of numbers is odd, let’s decide to have more numbers in max-heap than the Min Heap.

  2. insertNum(1): As ‘1’ is smaller than ‘3’, let’s insert it into the Max Heap.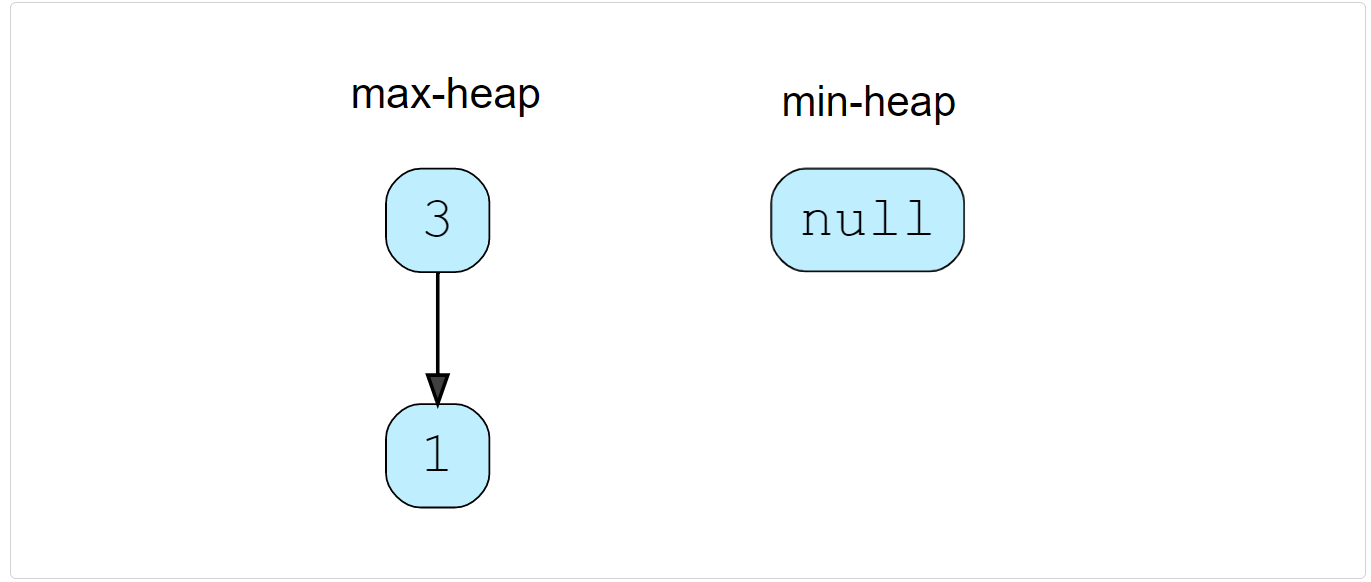

    Now, we have two elements in the Max Heap and no elements in Min Heap. Let’s take the largest element from the Max Heap and insert it into the Min Heap, to balance the number of elements in both heaps.

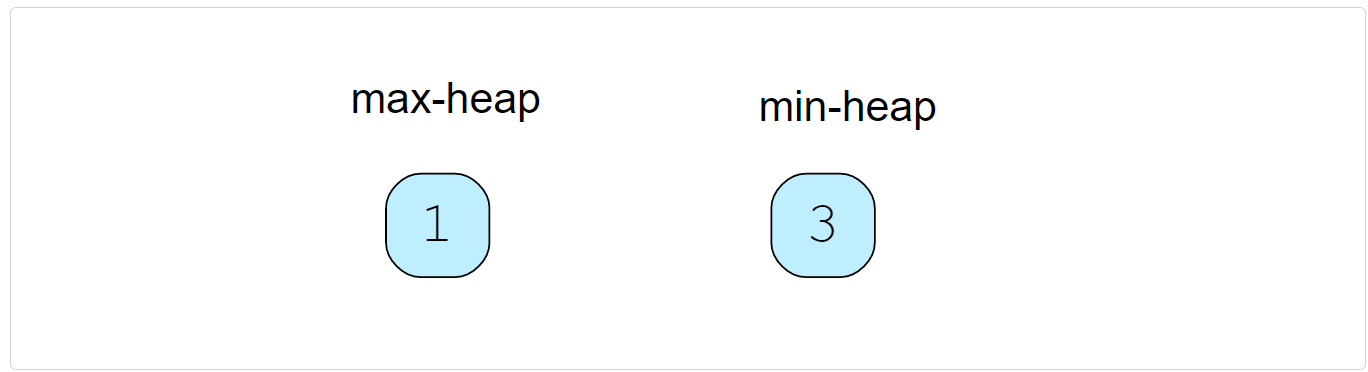
  3. findMedian(): As we have an even number of elements, the median will be the average of the top element of both the heaps -> (1+3)/2 = 2.0(1+3)/2=2.0

  4. insertNum(5): As ‘5’ is greater than the top element of the Max Heap, we can insert it into the Min Heap. After the insertion, the total count of elements will be odd. As we had decided to have more numbers in the Max Heap than the Min Heap, we can take the top (smallest) number from the Min Heap and insert it into the Max Heap.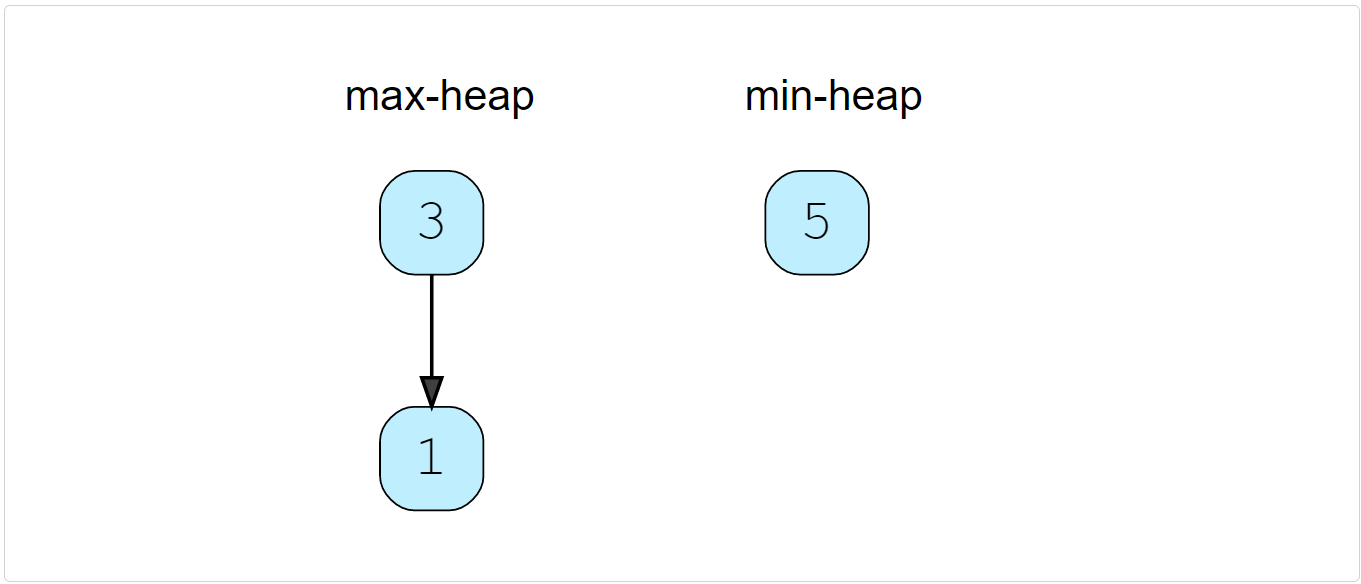

  5. findMedian(): Since we have an odd number of elements, the median will be the top element of Max Heap -> 3. An odd number of elements also means that the Max Heap will have one extra element than the Min Heap.

  6. insertNum(4): Insert ‘4’ into Min Heap.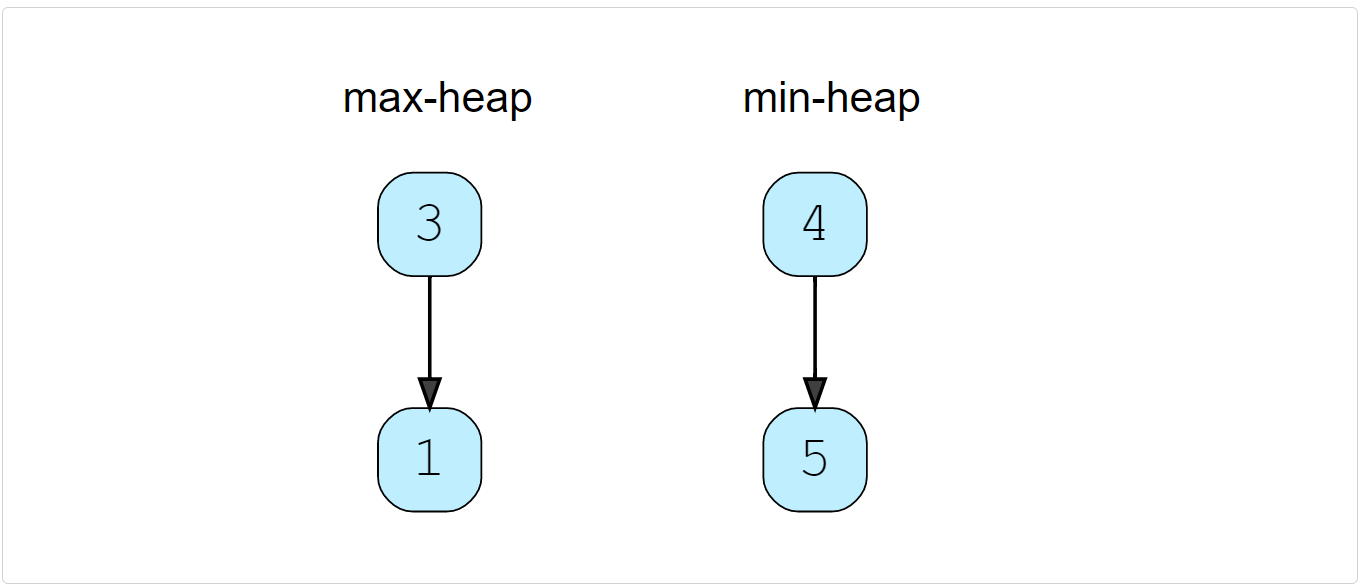

  7. findMedian(): As we have an even number of elements, the median will be the average of the top element of both the heaps -> (3+4)/2 = 3.5(3+4)/2=3.5

Code

Here is what our algorithm will look like:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
from heapq import *


class Solution:

    def __init__(self):
        self.maxHeap = []  # containing first half of numbers，# 存储小的一半的数字
        self.minHeap = []  # containing second half of numbers # 存储大的一半的数字

    def insertNum(self, num):
        if not self.maxHeap or -self.maxHeap[0] >= num:
            # heapq默认是小顶堆，所以要实现大顶堆的时候，就要取反
            heappush(self.maxHeap, -num)
        else:
            heappush(self.minHeap, num)

        # either both the heaps will have equal number of elements or max-heap will have one
        # more element than the min-heap
        if len(self.maxHeap) > len(self.minHeap) + 1:
            heappush(self.minHeap, -heappop(self.maxHeap))
        elif len(self.maxHeap) < len(self.minHeap):
            heappush(self.maxHeap, -heappop(self.minHeap))

    def findMedian(self):
        if len(self.maxHeap) == len(self.minHeap):
            # we have even number of elements, take the average of middle two elements
            return -self.maxHeap[0] / 2.0 + self.minHeap[0] / 2.0

        # because max-heap will have one more element than the min-heap
        return -self.maxHeap[0] / 1.0


def main():
    sol = Solution()
    sol.insertNum(3)
    sol.insertNum(1)
    print("The median is: " + str(sol.findMedian()))
    sol.insertNum(5)
    print("The median is: " + str(sol.findMedian()))
    sol.insertNum(4)
    print("The median is: " + str(sol.findMedian()))


main()


Time complexity

The time complexity of the insertNum() will be O(logN) due to the insertion in the heap. The time complexity of the findMedian() will be O(1) as we can find the median from the top elements of the heaps.

Space complexity

The space complexity will be O(N) because, as at any time, we will be storing all the numbers.

*Sliding Window Median (hard)

480. Sliding Window Median Design Gurus Educative.io

Problem Statement

Given an array of numbers and a number ‘k’, find the median of all the ‘k’ sized sub-arrays (or windows) of the array.

Example 1:

Input: nums=[1, 2, -1, 3, 5], k = 2
Output: [1.5, 0.5, 1.0, 4.0]
Explanation: Lets consider all windows of size ‘2’:

  • [1, 2, -1, 3, 5] -> median is 1.5
  • [1, 2, -1, 3, 5] -> median is 0.5
  • [1, 2, -1, 3, 5] -> median is 1.0
  • [1, 2, -1, 3, 5] -> median is 4.0

Example 2:

Input: nums=[1, 2, -1, 3, 5], k = 3
Output: [1.0, 2.0, 3.0]
Explanation: Lets consider all windows of size ‘3’:

  • [1, 2, -1, 3, 5] -> median is 1.0
  • [1, 2, -1, 3, 5] -> median is 2.0
  • [1, 2, -1, 3, 5] -> median is 3.0

Constraints:

  • 1 <= k <= nums.length <= 10^5
  • -2^31 <= nums[i] <= 2^31 - 1

Solution

This problem follows the Two Heaps pattern and share similarities with Find the Median of a Number Stream. We can follow a similar approach of maintaining a max-heap and a min-heap for the list of numbers to find their median.

The only difference is that we need to keep track of a sliding window of ‘k’ numbers. This means, in each iteration, when we insert a new number in the heaps, we need to remove one number from the heaps which is going out of the sliding window. After the removal, we need to rebalance the heaps in the same way that we did while inserting.

Here is the visual representation of the algorithm:

Code

Here is what our algorithm will look like:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
from heapq import *
import heapq


class Solution:
    def __init__(self):
        self.maxHeap, self.minHeap = [], []

    def findSlidingWindowMedian(self, nums, k):
        result = [0.0 for x in range(len(nums) - k + 1)]
        for i in range(0, len(nums)):
            if not self.maxHeap or nums[i] <= -self.maxHeap[0]:
                heappush(self.maxHeap, -nums[i])
            else:
                heappush(self.minHeap, nums[i])

            self.rebalance_heaps()

            if i - k + 1 >= 0:  # if we have at least 'k' elements in the sliding window
                # add the median to the the result array
                if len(self.maxHeap) == len(self.minHeap):
                    # we have even number of elements, take the average of middle two elements
                    result[i - k + 1] = -self.maxHeap[0] / \
                                        2.0 + self.minHeap[0] / 2.0
                else:  # because max-heap will have one more element than the min-heap
                    result[i - k + 1] = -self.maxHeap[0] / 1.0

                # remove the element going out of the sliding window
                elementToBeRemoved = nums[i - k + 1]
                if elementToBeRemoved <= -self.maxHeap[0]:
                    self.remove(self.maxHeap, -elementToBeRemoved)
                else:
                    self.remove(self.minHeap, elementToBeRemoved)

                self.rebalance_heaps()

        return result

    # removes an element from the heap keeping the heap property
    def remove(self, heap, element):
        ind = heap.index(element)  # find the element
        # copy the last element of the heap to this index and decrement the heap size
        heap[ind] = heap[-1]
        del heap[-1]

        # adjust the position of the element while maintaining the heap property.
        # we can use heapify to readjust the elements but that would be O(N),
        # instead, we will adjust only one element which will O(logN)
        if ind < len(heap):
            heapq._siftup(heap, ind)
            heapq._siftdown(heap, 0, ind)

    def rebalance_heaps(self):
        # either both the heaps will have equal number of elements or max-heap will have
        # one more element than the min-heap
        if len(self.maxHeap) > len(self.minHeap) + 1:
            heappush(self.minHeap, -heappop(self.maxHeap))
        elif len(self.maxHeap) < len(self.minHeap):
            heappush(self.maxHeap, -heappop(self.minHeap))


def main():
    sol = Solution()
    result = sol.findSlidingWindowMedian(
        [1, 2, -1, 3, 5], 2)
    print("Sliding window medians are: " + str(result))

    sol = Solution()
    result = sol.findSlidingWindowMedian(
        [1, 2, -1, 3, 5], 3)
    print("Sliding window medians are: " + str(result))


main()

Time complexity

The time complexity of our algorithm is O(N\K)* where ‘N’ is the total number of elements in the input array and ‘K’ is the size of the sliding window. This is due to the fact that we are going through all the ‘N’ numbers and, while doing so, we are doing two things:

  1. Inserting/removing numbers from heaps of size ‘K’. This will take O(logK)
  2. Removing the element going out of the sliding window. This will take O(K) as we will be searching this element in an array of size ‘K’ (i.e., a heap).

Space complexity

Ignoring the space needed for the output array, the space complexity will be O(K) because, at any time, we will be storing all the numbers within the sliding window.

Maximize Capital (hard)

Top Interview 150 | 502. IPO) Design Gurus Educative.io

Given a set of investment projects with their respective profits, we need to find the most profitable projects. We are given an initial capital and are allowed to invest only in a fixed number of projects. Our goal is to choose projects that give us the maximum profit. Write a function that returns the maximum total capital after selecting the most profitable projects.

We can start an investment project only when we have the required capital. After selecting a project, we can assume that its profit has become our capital, and that we have also received our capital back.

Example 1:

1
2
3
4
5
6
7
8
9
Input: Project Capitals=[0,1,2], Project Profits=[1,2,3], Initial Capital=1, Number of Projects=2

Output: 6

Explanation:
1. With initial capital of ‘1’, we will start the second project which will give us profit of ‘2’. Once we selected our first project, our total capital will become 3 (profit + initial capital).
2. With ‘3’ capital, we will select the third project, which will give us ‘3’ profit.

After the completion of the two projects, our total capital will be 6 (1+2+3).

Example 2:

1
2
3
4
5
6
7
8
9
10
11
Input: Project Capitals=[0,1,2,3], Project Profits=[1,2,3,5], Initial Capital=0, Number of Projects=3

Output: 8

Explanation:

1. With ‘0’ capital, we can only select the first project, bringing out capital to 1.
2. Next, we will select the second project, which will bring our capital to 3.
3. Next, we will select the fourth project, giving us a profit of 5.

After selecting the three projects, our total capital will be 8 (1+2+5).

Constraints:

  • 1 <= numberOfprojects <= 10^5
  • 0 <= initialCapital <= 10^9
  • n == profits.length
  • n == capital.length
  • 1 <= n <= 10^5
  • 0 <= profits[i] <= 10^4
  • 0 <= capital[i] <= 10^9

Solution

While selecting projects we have two constraints:

  1. We can select a project only when we have the required capital.
  2. There is a maximum limit on how many projects we can select.

Since we don’t have any constraint on time, we should choose a project, among the projects for which we have enough capital, which gives us a maximum profit. Following this greedy approach will give us the best solution.

While selecting a project, we will do two things:

  1. Find all the projects that we can choose with the available capital.
  2. From the list of projects in the 1st step, choose the project that gives us a maximum profit.

We can follow the Two Heaps approach similar to Find the Median of a Number Stream. Here are the steps of our algorithm:

  1. Add all project capitals to a min-heap, so that we can select a project with the smallest capital requirement.
  2. Go through the top projects of the min-heap and filter the projects that can be completed within our available capital. Insert the profits of all these projects into a max-heap, so that we can choose a project with the maximum profit.
  3. Finally, select the top project of the max-heap for investment.
  4. Repeat the 2nd and 3rd steps for the required number of projects.

Code

Here is what our algorithm will look like:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
from heapq import *


class Solution:
    def findMaximumCapital(self, capital, profits, numberOfProjects, initialCapital):
        minCapitalHeap = []
        maxProfitHeap = []

        # insert all project capitals to a min-heap
        for i in range(0, len(profits)):
            heappush(minCapitalHeap, (capital[i], i))

        # let's try to find a total of 'numberOfProjects' best projects
        availableCapital = initialCapital
        for _ in range(numberOfProjects):
            # find all projects that can be selected within the available capital and insert 
            # them in a max-heap
            while minCapitalHeap and minCapitalHeap[0][0] <= availableCapital:
                capital, i = heappop(minCapitalHeap)
                # push相反数来实现大顶堆
                heappush(maxProfitHeap, (-profits[i], i))

            # terminate if we are not able to find any project that can be completed within the 
            # available capital
            # 如果没有可以负担得起的项目，那就break，不然下面的会报错
            if not maxProfitHeap:
                break

            # select the project with the maximum profit
            availableCapital += -heappop(maxProfitHeap)[0]

        return availableCapital


def main():
    sol = Solution()
    print("Maximum capital: " +
          str(sol.findMaximumCapital([0, 1, 2], [1, 2, 3], 2, 1)))
    print("Maximum capital: " +
          str(sol.findMaximumCapital([0, 1, 2, 3], [1, 2, 3, 5], 3, 0)))


main()


Time complexity

Since, at the most, all the projects will be pushed to both the heaps once, the time complexity of our algorithm is O(NlogN + KlogN), where ‘N’ is the total number of projects and ‘K’ is the number of projects we are selecting.

Space complexity

The space complexity will be O(N) because we will be storing all the projects in the heaps.

Problem Challenge 1

436. Find Right Interval Design Gurus Educative.io

Next Interval (hard)

Given an array of intervals, find the next interval of each interval. In a list of intervals, for an interval ‘i’ its next interval ‘j’ will have the smallest ‘start’ greater than or equal to the ‘end’ of ‘i’.

Write a function to return an array containing indices of the next interval of each input interval. If there is no next interval of a given interval, return -1. It is given that none of the intervals have the same start point.

Example 1:

Input: Intervals [[2,3], [3,4], [5,6]]
Output: [1, 2, -1]
Explanation: The next interval of [2,3] is [3,4] having index ‘1’. Similarly, the next interval of [3,4] is [5,6] having index ‘2’. There is no next interval for [5,6] hence we have ‘-1’.

Example 2:

Input: Intervals [[3,4], [1,5], [4,6]]
Output: [2, -1, -1]
Explanation: The next interval of [3,4] is [4,6] which has index ‘2’. There is no next interval for [1,5] and [4,6].

Constraints:

  • 1 <= intervals.length <= 2 * 10^4
  • intervals[i].length == 2
  • -10^6 <= starti <= endi <= 10^6
  • The start point of each interval is unique.

Solution

A brute force solution could be to take one interval at a time and go through all the other intervals to find the next interval. This algorithm will take O(N^2) where ‘N’ is the total number of intervals. Can we do better than that?

We can utilize the Two Heaps approach. We can push all intervals into two heaps: one heap to sort the intervals on maximum start time (let’s call it maxStartHeap) and the other on maximum end time (let’s call it maxEndHeap). We can then iterate through all intervals of the `maxEndHeap’ to find their next interval. Our algorithm will have the following steps:

  1. Take out the top (having highest end) interval from the maxEndHeap to find its next interval. Let’s call this interval topEnd.
  2. Find an interval in the maxStartHeap with the closest start greater than or equal to the start of topEnd. Since maxStartHeap is sorted by ‘start’ of intervals, it is easy to find the interval with the highest ‘start’. Let’s call this interval topStart.
  3. Add the index of topStart in the result array as the next interval of topEnd. If we can’t find the next interval, add ‘-1’ in the result array.
  4. Put the topStart back in the maxStartHeap, as it could be the next interval of other intervals.
  5. Repeat the steps 1-4 until we have no intervals left in maxEndHeap.

Code

Here is what our algorithm will look like:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
from heapq import *


# class Interval:
#   def __init__(self, start, end):
#     self.start = start
#     self.end = end


class Solution:
    def findNextInterval(self, intervals):
        n = len(intervals)

        # heaps for finding the maximum start and end
        maxStartHeap, maxEndHeap = [], []

        result = [0 for x in range(n)]
        for endIndex in range(n):
            heappush(maxStartHeap, (-intervals[endIndex].start, endIndex))
            heappush(maxEndHeap, (-intervals[endIndex].end, endIndex))

        # go through all the intervals to find each interval's next interval
        for _ in range(n):
            # let's find the next interval of the interval which has the highest 'end'
            topEnd, endIndex = heappop(maxEndHeap)
            result[endIndex] = -1  # defaults to - 1
            if -maxStartHeap[0][0] >= -topEnd:
                topStart, startIndex = heappop(maxStartHeap)
                # find the the interval that has the closest 'start'
                while maxStartHeap and -maxStartHeap[0][0] >= -topEnd:
                    topStart, startIndex = heappop(maxStartHeap)
                result[endIndex] = startIndex
                # put the interval back as it could be the next interval of other intervals
                heappush(maxStartHeap, (topStart, startIndex))

        return result


def main():
    sol = Solution()
    result = sol.findNextInterval(
        [Interval(2, 3), Interval(3, 4), Interval(5, 6)])
    print("Next interval indices are: " + str(result))

    result = sol.findNextInterval(
        [Interval(3, 4), Interval(1, 5), Interval(4, 6)])
    print("Next interval indices are: " + str(result))


main()

Time complexity

The time complexity of our algorithm will be O(NlogN), where ‘N’ is the total number of intervals.

Space complexity

The space complexity will be O(N) because we will be storing all the intervals in the heaps.

Author：Hasuer

Link：https://hasuer.github.io/14-pattern-two-heaps/index.html

Publish date：May 14th 2024, 9:44:26 am

Update date：May 28th 2024, 11:29:05 am

License：本文采用知识共享署名-非商业性使用 4.0 国际许可协议进行许可

CATALOG
  1. 1. Introduction
  2. 2. Find the Median of a Number Stream (medium)
  3. 3. Introduction
    1. 3.1. Problem Statement
    2. 3.2. Solution
    3. 3.3. Code
      1. 3.3.1. Time complexity
      2. 3.3.2. Space complexity
  4. 4. *Sliding Window Median (hard)
    1. 4.1. Problem Statement
    2. 4.2. Solution
    3. 4.3. Code
      1. 4.3.1. Time complexity
      2. 4.3.2. Space complexity
  5. 5. Maximize Capital (hard)
    1. 5.1. Solution
    2. 5.2. Code
      1. 5.2.1. Time complexity
      2. 5.2.2. Space complexity
  6. 6. Problem Challenge 1
    1. 6.1. Next Interval (hard)
    2. 6.2. Solution
    3. 6.3. Code
      1. 6.3.1. Time complexity
      2. 6.3.2. Space complexity
Total : 41
2024
2022
2021
Interview
技术笔记 Grokking-Interview-Pattern