Hasuer's Studio.

8. Pattern Monotonic Stack

Grokking Interview Pattern Interview
Word count: 5.9kReading time: 34 min
2024/05/08

Introduction to Monotonic Stack

Definition of Monotonic Stack

A Monotonic Stack is a special kind of stack, a common data structure in computer science, which maintains its elements in a specific order. Unlike a traditional stack, where elements are placed on top of one another based on when they arrive, a Monotonic Stack ensures that the elements inside the stack remain in an increasing or decreasing order. This is achieved by enforcing specific push and pop rules, depending on whether we want an increasing or decreasing monotonic stack.

Relevance in Coding Interviews

Monotonic Stacks are powerful tools in coding interviews due to their unique capabilities. They are particularly effective when it comes to problems requiring us to find the next smaller or larger element in a sequence, often referred to as Next Greater Element (NGE) or Next Smaller Element (NSE) problems.

In the context of an interview, understanding and implementing a Monotonic Stack can not only help you solve the problem at hand but also demonstrate a strong grasp of data structures and algorithms to your interviewer. It shows that you can identify and apply the right tool for the task, a crucial ability for any software engineer.

Types of Monotonic Stacks

Monotonic Stacks can be broadly classified into two types:

  1. Monotonically Increasing Stack

A Monotonically Increasing Stack is a stack where elements are arranged in an ascending order from the bottom to the top. Here, every new element that’s pushed onto the stack is greater than or equal to the element below it. If a new element is smaller, we pop the elements from the top of the stack until we find an element smaller than or equal to the new element, or the stack is empty. This way, the stack always maintains an increasing order.

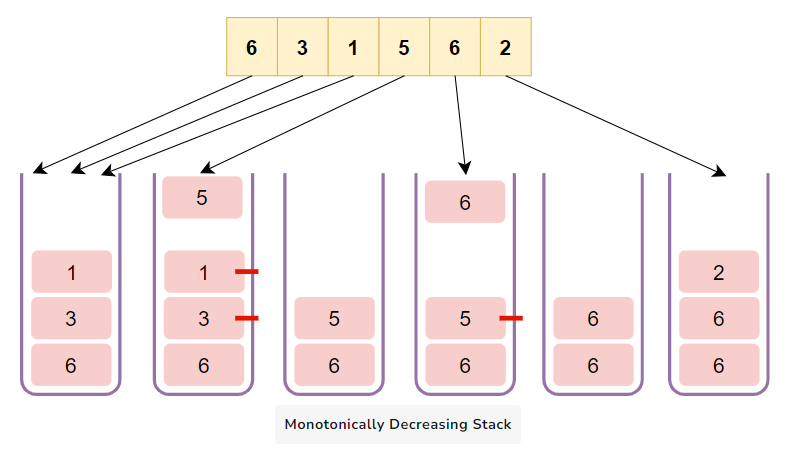
  1. Monotonically Decreasing Stack

Conversely, a Monotonically Decreasing Stack is a stack where elements are arranged in a descending order from the bottom to the top. When a new element arrives, if it’s larger than the element on the top, we keep popping the elements from the stack until we find an element that’s larger than or equal to the new element, or the stack is empty. This ensures that the stack always maintains a decreasing order.

Identifying Problems Suitable for Monotonic Stack

Recognizing when to use a Monotonic Stack is a vital skill. Here are some key aspects to consider:

Problem Characteristics

Monotonic Stacks are typically useful when dealing with problems that involve analyzing sequences or arrays, especially when you need to find the next or previous larger or smaller element for each element in the array. If you encounter a problem where the solution seems to require some sort of sequential step-by-step comparison, it’s likely a good candidate for using a Monotonic Stack.

Example Scenarios

One classic sign that a Monotonic Stack might be helpful is when the problem description mentions finding the “next greater element” or the “next smaller element” in an array. Problems that involve finding maximum areas, such as in histograms, can also be solved effectively using Monotonic Stacks. Remember, the key is to identify patterns where a sequential step-by-step comparison is necessary.

Constructing Monotonic Stacks

Understanding how to build Monotonic Stacks is key. We’ll break down this process for each type:

Code Template for Monotonically Increasing Stack

Here’s a general structure of a Monotonically Increasing Stack in pseudo-code:

1
2
3
4
5
create an empty stack
for each element in the array:
    while stack is not empty AND top of stack is more than the current element:
        pop the stack
    push the current element to stack

This logic guarantees that for each element, all larger elements preceding it get popped, leaving the next smaller element (if it exists) at the top of the stack.

Code Template for Monotonically Decreasing Stack

Similarly, here’s a template for a Monotonically Decreasing Stack:

1
2
3
4
5
create an empty stack
for each element in the array:
    while stack is not empty AND top of stack is less than the current element:
        pop the stack
    push the current element to stack

This structure ensures that for each element, all smaller elements preceding it get popped, leaving the next larger element (if it exists) at the top of the stack.

Explanation of the Code Templates

Both these templates work in a similar fashion. They loop through each element in the array, and for each one, they pop out the elements from the stack that are smaller (for increasing stack) or larger (for decreasing stack) than the current element. This ensures the stack stays monotonically increasing or decreasing.

Understanding Time Complexity

Grasping the time complexity of Monotonic Stacks is critical for efficiency. Let’s break it down for both types:

Time Complexity for Monotonically Increasing Stack

In a Monotonically Increasing Stack, each element from the input array is pushed and popped from the stack exactly once. Therefore, even though there is a loop inside a loop, no element is processed more than twice. Hence, the time complexity of building a Monotonically Increasing Stack is O(n), where N is the number of elements in the array.

Time Complexity for Monotonically Decreasing Stack

The situation is similar for a Monotonically Decreasing Stack. Each element is processed only twice, once for the push operation and once for the pop operation. As a result, the time complexity remains linear - O(n), with N being the size of the array.

To summarize, although the construction of Monotonic Stacks might look complex at first glance, they are impressively efficient. Each element in the input array is handled only twice (one push and one pop), making the overall time complexity linear.

Next, we’ll explore some practice problems to help you get more comfortable with Monotonic Stacks.

Note: 总结来说就是一般从前往后和从后往前都可以，但是应该是都需要一个结构（一般是一个map）来记录对应关系的，这道题的res就是起到了这个作用。但是一般都是从前往后遍历，在这个pattern中的例子基本都是从前往后遍历

Next Greater Element

496. Next Greater Element I Design Gurus

Problem Statement

Given two integer arrays nums1 and nums2, return an array answer such that answer[i] is the next greater number for every nums1[i] in nums2. The next greater element for an element x is the first element to the right of x that is greater than x. If there is no greater number, output -1 for that number.

The numbers in nums1 are all present in nums2 and nums2 is a permutation of nums1.

Examples

    • Input: nums1 = [4,2,6], nums2 = [6,2,4,5,3,7]
    • Output: [5,4,7]
    • Explanation: The next greater number for 4 is 5, for 2 is 4, and for 6 is 7 in nums2.
    • Input: nums1 = [9,7,1], nums2 = [1,7,9,5,4,3]
    • Output: [-1,9,7]
    • Explanation: The next greater number for 9 does not exist, for 7 is 9, and for 1 is 7 in nums2.
    • Input: nums1 = [5,12,3], nums2 = [12,3,5,4,10,15]
    • Output: [10,15,5]
    • Explanation: The next greater number for 5 is 10, for 12 is 15, and for 3 is 4 in nums2.

Constraints:

  • 1 <= nums1.length <= nums2.length <= 1000
  • 0 <= nums1[i], nums2[i] <= 10^4
  • All integers in nums1 and nums2 are unique.
  • All the integers of nums1 also appear in nums2.

Solution

This problem requires us to find the next greater element for each element in nums1 by searching nums2. The output array contains either the next greater element or -1 if no such element exists.

This problem can be solved using a Monotonic Stack and Hashmap. The Monotonic Stack helps to find the next greater element for each element in nums2. The Hashmap then maps each element to its next greater element.

这道题和Stack pattern 中的“Next greater element”都是构建了decreasing stack, 小的元素在栈顶，感觉是因为找的greater的元素？如果找的是smaller的元素是不是就是increaing stack 了, 不过前一道题是从后开始遍历的，这道题是从前开始遍历的. 经过实验，可以发现，前一道题也可以从前往后遍历，但是也需要像这道题一样需要一个hashmap来建立对应关系。同样的，这道题也可以像前一道题一样从后往前遍历。 总结来说就是一般从前往后和从后往前都可以，但是应该是都需要一个结构（一般是一个map）来记录对应关系的，这道题的res就是起到了这个作用。

Algorithm Walkthrough

  1. Initialize an empty stack and an empty hashmap.
  2. Loop through the nums2 array from left to right.
  3. For each number in nums2, while the stack is not empty and the current number is greater than the top element of the stack:
    • Pop the element from the stack and add an entry to the hashmap with the popped element as the key and the current number as the value.
  4. Push the current number onto the stack.
  5. After the loop, any numbers remaining on the stack do not have a next greater element, so for each of these numbers, add an entry to the hashmap with the number as the key and -1 as the value.
  6. Finally, create an output array by mapping each number in nums1 to its corresponding value in the hashmap.

Code

Here is the code for this algorithm:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
from collections import deque

class Solution:
    def nextGreaterElement(self, nums1, nums2):
        # Initialize stack and hashmap
        stack, hashmap = deque(), {}
        # stack, hashmap = [], {} # 原版，但是我比较习惯deque,而且不会对时间和空间复杂度有影响
        
        # Process each number in nums2
        for num in nums2:
            # Pop elements from the stack that are smaller than current number
            while stack and stack[-1] < num:
                hashmap[stack.pop()] = num # Remember the next greater element for num
            # Push current number onto stack
            stack.append(num)
            
        # Map the numbers in nums1 to their next greater number
        return [hashmap.get(num, -1) for num in nums1]

if __name__ == "__main__":
    solution = Solution()
    nums1 = [4,2,6]
    nums2 = [6,2,4,5,3,7]
    print(solution.nextGreaterElement(nums1, nums2))
    

# 下面这个采用了从后往前的遍历方式，但是可以发现对于这道题来说，从前往后遍历也需要一个map来记录，所以从前往后和从后往前都是可以的 ，但是要不要map辅助，就需要看题目了。
# 下面这个也过了leetcode,并且时间和空间上没有差别
# 总结来说就是一般从前往后和从后往前都可以，但是应该是都需要一个结构（一般是一个map）来记录对应关系的，这道题的res就是起到了这个作用。**但是一般都是从前往后遍历**
from collections import deque


class Solution:
    def nextGreaterElement(self, nums1, nums2):
        # Initialize stack and hashmap
        stack = deque()
        # stack = [] # 原版，但是我比较习惯deque,而且不会对时间和空间复杂度有影响
        greater_index_for_nums2 = {}
        # Process each number in nums2
        for i in range(len(nums2) - 1, -1, -1):
            # Pop elements from the stack that are smaller than current number
            # 因为找的是greater所以这里的判断应该就是<=的都弹出,直到遇到了大于的
            while stack and stack[-1] <= nums2[i]:
                stack.pop()
            if stack:
                greater_index_for_nums2[nums2[i]] = stack[-1]
            stack.append(nums2[i])
        # print(greater_index_for_nums2)
        # Map the numbers in nums1 to their next greater number
        return [greater_index_for_nums2.get(num, -1) for num in nums1]


if __name__ == "__main__":
    solution = Solution()
    nums1 = [4, 2, 6]
    nums2 = [6, 2, 4, 5, 3, 7]
    print(solution.nextGreaterElement(nums1, nums2))
    nums1 = [9, 7, 1]
    nums2 = [1, 7, 9, 5, 4, 3]
    print(solution.nextGreaterElement(nums1, nums2))
    nums1 = [5, 12, 3]
    nums2 = [12, 3, 5, 4, 10, 15]
    print(solution.nextGreaterElement(nums1, nums2))


Time and Space Complexity

The time complexity of this algorithm is O(n) , where N is the length of nums2, since each element is pushed and popped from the stack exactly once. The space complexity is O(n) as well, due to the additional space needed for the stack and the hashmap.

Daily Temperatures

739. Daily Temperatures Design Gurus

Problem Statement

Given an array of integers temperatures representing daily temperatures, your task is to calculate how many days you have to wait until a warmer temperature. If there is no future day for which this is possible, put 0 instead.

Examples

    • Input: temperatures = [70, 73, 75, 71, 69, 72, 76, 73]
    • Output: [1, 1, 4, 2, 1, 1, 0, 0]
    • Explanation: The first day’s temperature is 70 and the next day’s temperature is 73 which is warmer. So for the first day, you only have to wait for 1 day to get a warmer temperature. Hence, the first element in the result array is 1. The same process is followed for the rest of the days.
    • Input: temperatures = [73, 72, 71, 70]
    • Output: [0, 0, 0, 0]
    • Explanation: As we can see, the temperature is decreasing every day. So, there is no future day with a warmer temperature. Hence, all the elements in the result array are 0.
    • Input: temperatures = [70, 71, 72, 73]
    • Output: [1, 1, 1, 0]
    • Explanation: For the first three days, the next day is warmer. But for the last day, there is no future day with a warmer temperature. Hence, the result array is [1, 1, 1, 0].

Constraints:

  • 1 <= temperatures.length <= 10^5
  • 30 <= temperatures[i] <= 100

Solution

This problem is quite similar to ‘Next Greater Element’. We can use a monotonically decreasing stack to find the next higher temperature.

We will use a stack to store the indices of the temperatures array. We iterate over the array, and for each temperature, we check whether the current temperature is greater than the temperature at the index on the top of the stack. If it is, we update the corresponding position in the result array and pop the index from the stack.

Algorithm Walkthrough

  1. Initialize an empty stack to store the indices of the temperatures array. Also, initialize a result array of the same length as temperatures with all values set to 0.
  2. Iterate over the temperatures array. For each temperature:
    • While the stack is not empty and the current temperature is greater than the temperature at the index on the top of the stack, set the value in the result array at the top index of the stack to the difference between the current index and the top index of the stack. Pop the index from the stack.
    • Push the current index onto the stack.
  3. Return the result array.

Code

Here is how we can implement this algorithm:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
from collections import deque


class Solution:
    def dailyTemperatures(self, temperatures):
        stack = deque()  # Initialize an empty stack to store indices of temperatures.
        # stack = [] # 原版，但是我比较习惯deque,而且不会对时间和空间复杂度有影响
        res = [0] * len(temperatures)  # Initialize a result list with zeros.

        for i in range(len(temperatures)):
            while stack and temperatures[i] > temperatures[stack[-1]]:
                # While the stack is not empty and the current temperature is higher
                # than the temperature at the index stored at the top of the stack:
                idx = stack.pop()  # Pop the top index from the stack.
                res[idx] = i - idx  # Calculate the number of days until warmer temperature.
            stack.append(i)  # Push the current index onto the stack.

        return res


if __name__ == "__main__":
    solution = Solution()
    print(solution.dailyTemperatures([70, 73, 75, 71, 69, 72, 76, 73]))  # Output: [1, 1, 4, 2, 1, 1, 0, 0]
    print(solution.dailyTemperatures([73, 72, 71, 70]))  # Output: [0, 0, 0, 0]
    print(solution.dailyTemperatures([70, 71, 72, 73]))  # Output: [1, 1, 1, 0]
    
    
# 当然也可以从后往前遍历，也可以过leetcode,并且时间和空间上没有任何差别
from collections import deque


class Solution:
    def dailyTemperatures(self, temperatures):
        stack = deque()  # Initialize an empty stack to store indices of temperatures.
        res = [0] * len(temperatures)  # Initialize a result list with zeros.

        for i in range(len(temperatures) - 1, -1, -1):
            idx = 0
            # 这边是把不符合的（小于或者等于）的剔除，所以留下来的是warmer的温度
            while stack and temperatures[i] >= temperatures[stack[-1]]:
                # While the stack is not empty and the current temperature is higher
                # than the temperature at the index stored at the top of the stack:
                idx = stack.pop()  # Pop the top index from the stack.
            if stack:
                res[i] = stack[-1] - i  # Calculate the number of days until warmer temperature.
            stack.append(i)  # Push the current index onto the stack.

        return res


if __name__ == "__main__":
    solution = Solution()
    print(solution.dailyTemperatures([70, 73, 75, 71, 69, 72, 76, 73]))  # Output: [1, 1, 4, 2, 1, 1, 0, 0]
    print(solution.dailyTemperatures([73, 72, 71, 70]))  # Output: [0, 0, 0, 0]
    print(solution.dailyTemperatures([70, 71, 72, 73]))  # Output: [1, 1, 1, 0]


Time and Space Complexity

The time complexity of the algorithm is O(n), where N is the size of the temperatures array, since we process each temperature once. The space complexity is also O(n), where N is the size of the temperatures array, due to the extra space used by the stack and the output list.

Remove Nodes From Linked List

2487. Remove Nodes From Linked List Design Gurus

Problem Statement

Given the head node of a singly linked list, modify the list such that any node that has a node with a greater value to its right gets removed. The function should return the head of the modified list.

Examples:

  1. Input: 5 -> 3 -> 7 -> 4 -> 2 -> 1
    Output: 7 -> 4 -> 2 -> 1
    Explanation: 5 and 3 are removed as they have nodes with larger values to their right.
  2. Input: 1 -> 2 -> 3 -> 4 -> 5
    Output: 5
    Explanation: 1, 2, 3, and 4 are removed as they have nodes with larger values to their right.
  3. Input: 5 -> 4 -> 3 -> 2 -> 1
    Output: 5 -> 4 -> 3 -> 2 -> 1
    Explanation: None of the nodes are removed as none of them have nodes with larger values to their right.

Constraints:

  • The number of the nodes in the given list is in the range [1, 10^5].
  • 1 <= Node.val <= 1010^5

Solution

We can the monotonic stack strategy to keep track of the highest-valued nodes in the linked list, ensuring that any node with a higher value to its right gets removed.

Starting from the head of the list, we will traverse each node. At each node, we will check the value of the node against the node at the top of the stack. If the current node has a higher value, we will pop the top value from the stack. We will keep repeating this until we encounter a node with a higher value or the stack is empty. Then, the current node is pushed onto the stack. This process ensures that the stack only contains nodes in decreasing order from bottom to top.

Detailed Walkthrough:

  1. Create an empty stack, stack.

  2. Initialize cur with the head of the linked list.

  3. Enter a loop that continues until cur becomes null:

    a. Enter an inner loop that continues as long as cur‘s value is greater than the value of the node at the top of stack:

    • Pop the top node from stack.

    b. If stack is not empty, set the next of the node at the top of stack to cur.

    c. Push cur onto stack.

    d. Move cur to the next node in the linked list.

  4. After exiting the loop, return the bottom node of stack as the head of the modified linked list. If stack is empty, return null.

Code

Here is how we can implement this algorithm:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
from collections import deque


# class Node:
#     def __init__(self, value, next=None):
#         self.val = value
#         self.next = next


class Solution:
    def removeNodes(self, head):
        stack = deque()  # Create an empty stack to store nodes in descending order
        # stack = [] # 原版，但是我比较习惯deque,而且不会对时间和空间复杂度有影响

        cur = head
        while cur:
            while stack and stack[-1].val < cur.val:
                stack.pop()  # Remove nodes from the stack that are smaller than the current node
            if stack:
                stack[-1].next = cur  # Update the next pointer of the top node in the stack
            stack.append(cur)  # Push the current node onto the stack
            cur = cur.next

        return stack.popleft() if stack else None  # Return the head of the modified list, or None if the stack is empty
        # return stack[0] if stack else None  # 这两句话都可以


# Testing the solution
solution = Solution()

# Creating the linked list 5 -> 3 -> 7 -> 4 -> 2 -> 1
head1 = Node(5)
head1.next = Node(3)
head1.next.next = Node(7)
head1.next.next.next = Node(4)
head1.next.next.next.next = Node(2)
head1.next.next.next.next.next = Node(1)
head1 = solution.removeNodes(head1)

# Printing the modified list: 7 -> 4 -> 2 -> 1
node = head1
while node:
    print(node.val, end=" -> " if node.next else "\n")
    node = node.next

Time and Space Complexity

The time complexity of this algorithm is O(n), where n is the number of nodes in the linked list. This is because every node is visited once while traversing the list. The inner loop may seem to increase the time complexity, but in fact, it doesn’t, because each node is pushed and popped from the stack at most once, so the total operations are still proportional to n.

The space complexity is also O(n). This is due to the extra space required for the stack. In the worst-case scenario (when the list is sorted in ascending order), all the nodes will be pushed onto the stack, requiring n space.

Therefore, we say the algorithm is linear in both time and space complexity.

Remove All Adjacent Duplicates In String

1047. Remove All Adjacent Duplicates In String Design Gurus

Problem Statement

Given a string S, remove all adjacent duplicate characters recursively to generate the resultant string.

Examples

    • Input: s = "abccba"
    • Output: ""
    • Explanation: First, we remove “cc” to get “abba”. Then, we remove “bb” to get “aa”. Finally, we remove “aa” to get an empty string.
    • Input: s = "foobar"
    • Output: "fbar"
    • Explanation: We remove “oo” to get “fbar”.
    • Input: s = "abcd"
    • Output: "abcd"
    • Explanation: No adjacent duplicates so no changes.

Constraints:

  • 1 <= s.length <= 10^5
  • s consists of lowercase English letters.

Solution

This problem can be solved efficiently using a stack, which can mimic the process of eliminating adjacent duplicates.

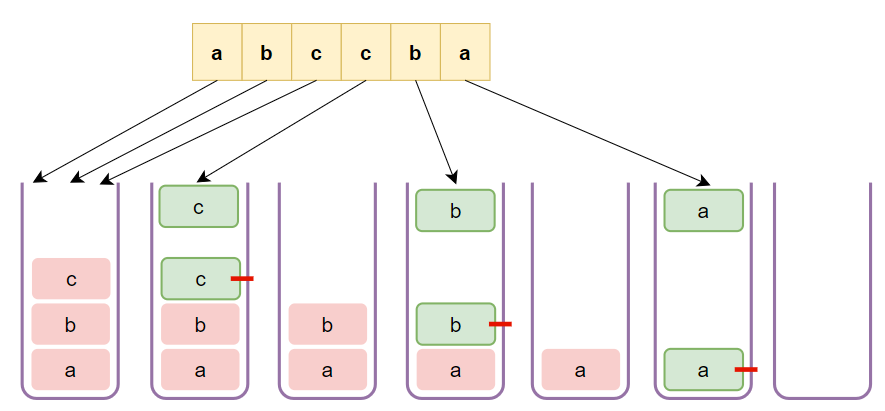
Algorithm Walkthrough

  1. Initialize an empty stack.
  2. Loop through the characters in the given string s.
  3. For each character:
    • If the stack is not empty and the current character is the same as the top character on the stack, pop the character from the stack.
    • Otherwise, push the current character onto the stack.
  4. Finally, build the result string from the characters remaining on the stack.

Code

Here is the code for this algorithm:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
from collections import deque


class Solution:
    def removeDuplicates(self, s: str) -> str:
        # Initialize stack
        stack = deque()
        # stack = [] # 原版，但是我比较习惯deque,而且不会对时间和空间复杂度有影响

        # Process each character in s
        for c in s:
            # If the stack is not empty and the current character is the same as the top of the stack,
            # pop the character from the stack
            # 注意，这里只会消去重复出现偶数次的，如果是“acccd"那么结果是"acd",所以应该使用if
            # 如果是while else循环的话，那么"abccba"会输出”abcba“
            if stack and c == stack[-1]:
                stack.pop()
            else:  # Push the current character onto the stack
                stack.append(c)

        # Join the stack to a string
        return ''.join(stack)


if __name__ == "__main__":
    solution = Solution()
    print(solution.removeDuplicates("abccba"))  # Output: ""
    print(solution.removeDuplicates("foobar"))  # Output: "fbar"
    print(solution.removeDuplicates("abcd"))  # Output: "abcd"
    print(solution.removeDuplicates("abcccd"))  # Output: "abcd"

Time and Space Complexity

The time complexity of this algorithm is O(n), where N is the length of s, because we perform one operation per character in s. The space complexity is also O(n), as in the worst case, every character in s is pushed onto the stack.

Remove All Adjacent Duplicates in String II

1209. Remove All Adjacent Duplicates in String II Design Gurus

Problem Statement

You are given a string s and an integer k. Your task is to remove groups of identical, consecutive characters from the string such that each group has exactly k characters. The removal of groups should continue until it’s no longer possible to make any more removals. The result should be the final version of the string after all possible removals have been made.

Examples

    • Input: s = "abbbaaca", k = 3
    • Output: "ca"
    • Explanation: First, we remove “bbb” to get “aaaca”. Then, we remove “aaa” to get “ca”.
    • Input: s = "abbaccaa", k = 3
    • Output: "abbaccaa"
    • Explanation: There are no instances of 3 adjacent characters being the same.
    • Input: s = "abbacccaa", k = 3
    • Output: "abb"
    • Explanation: First, we remove “ccc” to get “abbaaa”. Then, we remove “aaa” to get “abb”.

Constraints:

  • 1 <= s.length <= 10^5
  • 2 <= k <= 10^4
  • s only contains lowercase English letters.

Solution

This problem can be solved by using a stack to keep track of the characters and their counts. We iterate through the string and add each character and its count to the stack. If the count of the top character of the stack becomes k, we remove that entry from the stack. The result string is then constructed from the remaining characters in the stack.

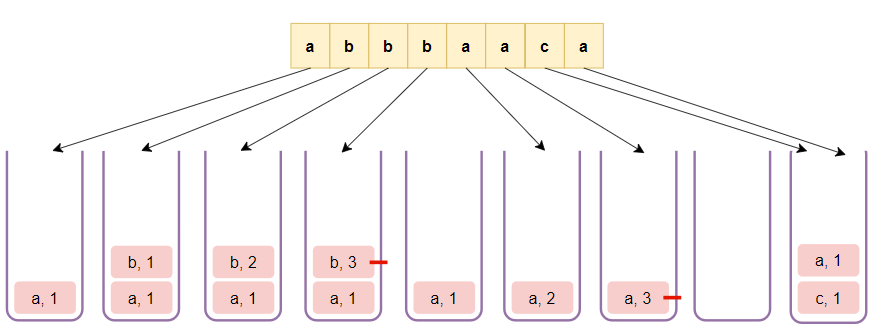
Algorithm Walkthrough

  1. Initialize an empty stack. Each entry in the stack is a pair consisting of a character and its count.
  2. Loop through the characters in s.
  3. For each character:
    • If the stack is not empty and the current character is the same as the top character on the stack, increment the count of the top character.
    • Otherwise, add the current character and a count of 1 to the stack.
    • If the count of the top character on the stack is k, pop the top character from the stack.
  4. Build the result string from the characters remaining on the stack.

Code

Here is how we can implement this algorithm:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
from collections import deque


class Solution:
    def removeDuplicates(self, s: str, k: int) -> str:
        stack = deque()  # Initialize an empty stack to track characters and their counts.
        # stack = [] # 原版，但是我比较习惯deque,而且不会对时间和空间复杂度有影响

        for c in s:
            # If the stack is not empty and the current character is the same as the top of the stack.
            if stack and stack[-1][0] == c:
                stack[-1][1] += 1  # Increment the count of the top character in the stack.
            else:
                stack.append([c, 1])  # Otherwise, push a new character-count pair onto the stack.

            if stack[-1][1] == k:  # If the count of the top character in the stack reaches 'k'.
                stack.pop()  # Remove it from the stack.

        return ''.join(c * n for c, n in stack)  # Reconstruct the string from the characters remaining in the stack.


if __name__ == "__main__":
    solution = Solution()
    print(solution.removeDuplicates("abbbaaca", 3))  # Output: "ca"
    print(solution.removeDuplicates("abbaccaa", 3))  # Output: "abbaccaa"
    print(solution.removeDuplicates("abbacccaa", 3))  # Output: "abbaa"
    print(solution.removeDuplicates("abbaccccaa", 3))  # Output: "abbacaa"

Time and Space Complexity

The time complexity of this algorithm is O(n), where N is the length of s, as we perform one operation per character. The space complexity is also O(n), as in the worst case, all characters are pushed onto the stack.

Remove K Digits

402. Remove K Digits Design Gurus

Problem Statement

Given a non-negative integer represented as a string num and an integer k, delete k digits from num to obtain the smallest possible integer. Return this minimum possible integer as a string.

Examples

    • Input: num = "1432219", k = 3
    • Output: "1219"
    • Explanation: The digits removed are 4, 3, and 2 forming the new number 1219 which is the smallest.
    • Input: num = "10200", k = 1
    • Output: "200"
    • Explanation: Removing the leading 1 forms the smallest number 200.
    • Input: num = "1901042", k = 4
    • Output: "2"
    • Explanation: Removing 1, 9, 1, and 4 forms the number 2 which is the smallest possible.

Constraints:

  • 1 <= k <= num.length <= 10^5
  • num consists of only digits.
  • num does not have any leading zeros except for the zero itself.

Solution

The idea is to keep removing the peak digit from the number num. The peak digit in a number is a digit after which the next digit is smaller. By doing so, we are always trying to minimize the leftmost digit which will give us the smallest possible number.

We can use a monotonically increasing stack to keep track of the decreasing peak digits.

Algorithm Walkthrough

  1. Initialize an empty stack.
  2. Iterate over the digits in num.
  3. For each digit:
    • While k is greater than 0, the stack is not empty and the current digit is smaller than the top digit on the stack, pop the top digit from the stack and decrease k by 1.
    • Push the current digit onto the stack.
  4. If k is still greater than 0, pop k digits from the stack.
  5. Build the result string from the digits in the stack. Remove the leading zeros.
  6. If the result string is empty, return “0”. Otherwise, return the result string.

Code

Here is how we can implement this algorithm:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
# 官方答案，时间复杂度比较小
from collections import deque


class Solution:
    def removeKdigits(self, num: str, k: int) -> str:
        stack = deque()
        # stack = [] # 原版，但是我比较习惯deque,而且不会对时间和空间复杂度有影响

        for digit in num:
            # 没有转化为int，确实也不需要
            while k > 0 and stack and stack[-1] > digit:
                stack.pop()
                k -= 1

            stack.append(digit)

        # Truncate the remaining K digits
        # 在pycharm中deque也可以使用[:]来切分,但是在leetcode中deque不可以
        # stack = stack[:-k] if k > 0 else stack
        # 所以如果要用deque的话就要这样写
        while stack and k:
            stack.pop()
            k -= 1 # 这个忘记写了

        # Remove any leading zeros
        return "".join(stack).lstrip("0") or "0"


if __name__ == "__main__":
    solution = Solution()
    print(solution.removeKdigits("1432219", 3))  # Output: "1219"
    print(solution.removeKdigits("10200", 1))  # Output: "200"
    print(solution.removeKdigits("1901042", 4))  # Output: "2"


# 自己写的，能过前三个测试用例（官方给的），但是第四个过不了（leetcode）
from collections import deque


class Solution:
    def removeKdigits(self, num: str, k: int) -> str:
        stack = deque()
        
        for c in num:
            while stack and int(c) < stack[-1] and k:
                stack.pop()
                k -= 1
            if int(c) > 0 or stack:
                stack.append(int(c))
        if stack:
            return "".join(str(c) for c in stack)
        return "0"


if __name__ == "__main__":
    solution = Solution()
    print(solution.removeKdigits("1432219", 3))  # Output: "1219"
    print(solution.removeKdigits("10200", 1))  # Output: "200"
    print(solution.removeKdigits("1901042", 4))  # Output: "2"
    
# 自己写的v2,最后一个测试用例过不了（leetcode）
from collections import deque


class Solution:
    def removeKdigits(self, num: str, k: int) -> str:
        stack = deque()
        for c in num:
            while stack and int(c) < stack[-1] and k:
                stack.pop()
                k -= 1
            if int(c) > 0 or stack:
                stack.append(int(c))
        while stack and k:
            stack.pop()
        if stack:
            return "".join(str(c) for c in stack)
        return "0"


if __name__ == "__main__":
    solution = Solution()
    print(solution.removeKdigits("1432219", 3))  # Output: "1219"
    print(solution.removeKdigits("10200", 1))  # Output: "200"
    print(solution.removeKdigits("1901042", 4))  # Output: "2"
    print(solution.removeKdigits("9", 1))  # Output: "0"
    print(solution.removeKdigits("112", 1))  # Output: "11"
    
    
# 自己写的v3，过了leetcode
from collections import deque


class Solution:
    def removeKdigits(self, num: str, k: int) -> str:
        stack = deque()
        for c in num:
            while stack and int(c) < stack[-1] and k:
                stack.pop()
                k -= 1
            if int(c) > 0 or stack:
                stack.append(int(c))
        while stack and k:
            stack.pop()
            k -= 1 # 这个忘记写了
        if stack:
            return "".join(str(c) for c in stack)
        return "0"


if __name__ == "__main__":
    solution = Solution()
    print(solution.removeKdigits("1432219", 3))  # Output: "1219"
    print(solution.removeKdigits("10200", 1))  # Output: "200"
    print(solution.removeKdigits("1901042", 4))  # Output: "2"
    print(solution.removeKdigits("9", 1))  # Output: "0"
    print(solution.removeKdigits("112", 1))  # Output: "11"

Time and Space Complexity

  • Time: O(n) where N is the number of digits in input.
  • Space: O(n) to store stack.

Author：Hasuer

Link：https://hasuer.github.io/8-pattern-monotonic-stack/index.html

Publish date：May 8th 2024, 5:18:45 pm

Update date：May 28th 2024, 11:27:56 am

License：本文采用知识共享署名-非商业性使用 4.0 国际许可协议进行许可

CATALOG
  1. 1. Introduction to Monotonic Stack
    1. 1.1. Definition of Monotonic Stack
    2. 1.2. Types of Monotonic Stacks
    3. 1.3. Identifying Problems Suitable for Monotonic Stack
    4. 1.4. Constructing Monotonic Stacks
    5. 1.5. Understanding Time Complexity
  2. 2. Next Greater Element
    1. 2.1. Problem Statement
    2. 2.2. Solution
    3. 2.3. Code
    4. 2.4. Time and Space Complexity
  3. 3. Daily Temperatures
    1. 3.1. Problem Statement
    2. 3.2. Solution
    3. 3.3. Code
    4. 3.4. Time and Space Complexity
  4. 4. Remove Nodes From Linked List
    1. 4.1. Problem Statement
    2. 4.2. Solution
    3. 4.3. Code
    4. 4.4. Time and Space Complexity
  5. 5. Remove All Adjacent Duplicates In String
    1. 5.1. Problem Statement
    2. 5.2. Solution
    3. 5.3. Code
    4. 5.4. Time and Space Complexity
  6. 6. Remove All Adjacent Duplicates in String II
    1. 6.1. Problem Statement
    2. 6.2. Solution
    3. 6.3. Code
    4. 6.4. Time and Space Complexity
  7. 7. Remove K Digits
    1. 7.1. Problem Statement
    2. 7.2. Solution
    3. 7.3. Code
    4. 7.4. Time and Space Complexity
Total : 41
2024
2022
2021
Interview
技术笔记 Grokking-Interview-Pattern