4. Pattern Merge Intervals

Grokking Interview Pattern Interview

Word count: 5.6kReading time: 34 min

 2024/05/04 

Introduction

This pattern describes an efficient technique to deal with overlapping intervals. In a lot of problems involving intervals, we either need to find overlapping intervals or merge intervals if they overlap.

Given two intervals (‘a’ and ‘b’), there will be six different ways the two intervals can relate to each other:

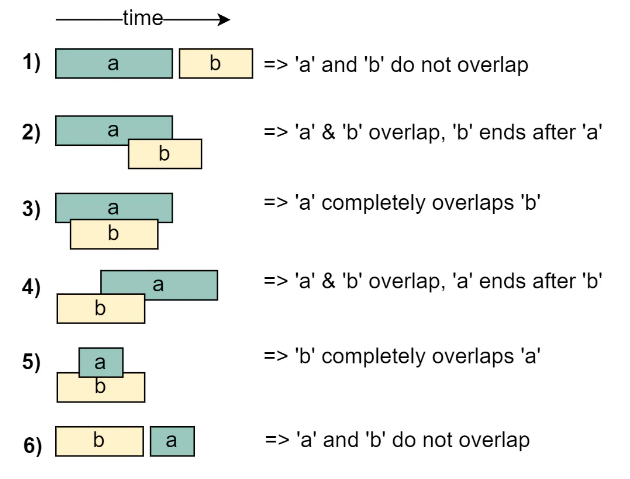
Understanding the above six cases will help us in solving all intervals related problems. Let’s jump onto our first problem to understand the Merge Interval pattern.

*Merge Intervals (medium)

Top Interview 150 | 56. Merge Intervals Similar | Top Interview 150 | 452. Minimum Number of Arrows to Burst Balloons Design Gurus Educative.io

Problem Statement

Given a list of intervals, merge all the overlapping intervals to produce a list that has only mutually exclusive intervals.

Example 1:

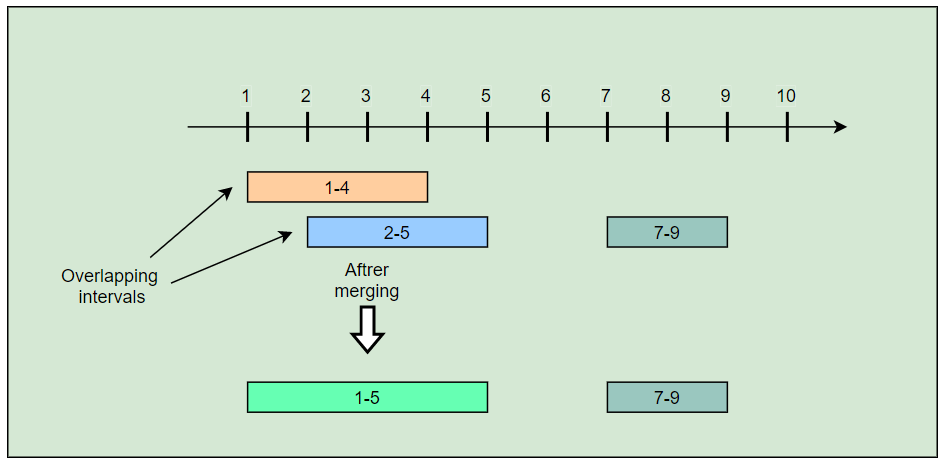
Intervals: [[1,4], [2,5], [7,9]]
Output: [[1,5], [7,9]]
Explanation: Since the first two intervals [1,4] and [2,5] overlap, we merged them into 
one [1,5].

Example 2:

1
2
3

Intervals: [[6,7], [2,4], [5,9]]
Output: [[2,4], [5,9]]
Explanation: Since the intervals [6,7] and [5,9] overlap, we merged them into one [5,9].

Example 3:

Intervals: [[1,4], [2,6], [3,5]]
Output: [[1,6]]
Explanation: Since all the given intervals overlap, we merged them into one.

onstraints:

1 <= intervals.length <= 10^4
intervals[i].length == 2
0 <= start_i <= end_i <= 10^4

Solution

Let’s take the example of two intervals (‘a’ and ‘b’) such that a.start <= b.start. There are four possible scenarios:

Our goal is to merge the intervals whenever they overlap. For the above-mentioned three overlapping scenarios (2, 3, and 4), this is how we will merge them:

The diagram above clearly shows a merging approach. Our algorithm will look like this:

Sort the intervals on the start time to ensure a.start <= b.start
If ‘a’ overlaps ‘b’ (i.e. b.start <= a.end), we need to merge them into a new interval ‘c’ such that:

1 2	c.start = a.start c.end = max(a.end, b.end)

We will keep repeating the above two steps to merge ‘c’ with the next interval if it overlaps with ‘c’.

Code

Here is what our algorithm will look like:

#class Interval:
#  def __init__(self, start, end):
#    self.start = start
#    self.end = end

def print_interval(i):
  print("[" + str(i.start) + ", " + str(i.end) + "]", end='')


class Solution:
  def merge(self, intervals):
    if len(intervals) < 2:
      return intervals

    # sort the intervals on the start time
    intervals.sort(key=lambda x: x.start)

    mergedIntervals = []
    start = intervals[0].start
    end = intervals[0].end
    for i in range(1, len(intervals)):
      interval = intervals[i]
      if interval.start <= end:  # overlapping intervals, adjust the 'end'
        end = max(interval.end, end)
      else:  # non-overlapping interval, add the previous interval and reset
        mergedIntervals.append(Interval(start, end))
        start = interval.start
        end = interval.end

    # add the last interval
    mergedIntervals.append(Interval(start, end))
    return mergedIntervals


def main():
  sol = Solution()
  print("Merged intervals: ", end='')
  for i in sol.merge([Interval(1, 4), Interval(2, 5), Interval(7, 9)]):
    print_interval(i)
  print()

  print("Merged intervals: ", end='')
  for i in sol.merge([Interval(6, 7), Interval(2, 4), Interval(5, 9)]):
    print_interval(i)
  print()

  print("Merged intervals: ", end='')
  for i in sol.merge([Interval(1, 4), Interval(2, 6), Interval(3, 5)]):
    print_interval(i)
  print()


main()

Time complexity

The time complexity of the above algorithm is O(N \ logN)*, where ‘N’ is the total number of intervals. We are iterating the intervals only once which will take O(N), in the beginning though, since we need to sort the intervals, our algorithm will take O(N \ logN)*.

Space complexity

The space complexity of the above algorithm will be O(N) as we need to return a list containing all the merged intervals. We will also need O(N) space for sorting. For Java, depending on its version, Collection.sort() either uses Merge sort or Timsort, and both these algorithms need O(N) space. Overall, our algorithm has a space complexity of O(N).

*Insert Interval (medium)

Top Interview 150 |57. Insert Interval Design Gurus Educative.io

Problem Statement

Given a list of non-overlapping intervals sorted by their start time, insert a given interval at the correct position and merge all necessary intervals to produce a list that has only mutually exclusive intervals.

Example 1:

1
2
3

Input: Intervals=[[1,3], [5,7], [8,12]], New Interval=[4,6]
Output: [[1,3], [4,7], [8,12]]
Explanation: After insertion, since [4,6] overlaps with [5,7], we merged them into one [4,7].

Example 2:

1
2
3

Input: Intervals=[[1,3], [5,7], [8,12]], New Interval=[4,10]
Output: [[1,3], [4,12]]
Explanation: After insertion, since [4,10] overlaps with [5,7] & [8,12], we merged them into [4,12].

Example 3:

1
2
3

Input: Intervals=[[2,3],[5,7]], New Interval=[1,4]
Output: [[1,4], [5,7]]
Explanation: After insertion, since [1,4] overlaps with [2,3], we merged them into one [1,4].

Constraints:

1 <= intervals.length <= 10^4
intervals[i].length == 2
0 <= start_i <= end_i <= 10^5
intervals is sorted by start_i in ascending order.
newInterval.length == 2
0 <= start <= end <= 105

Solution

If the given list was not sorted, we could have simply appended the new interval to it and used the merge() function from Merge Intervals. But since the given list is sorted, we should try to come up with a solution better than O(N \ logN)*

When inserting a new interval in a sorted list, we need to first find the correct index where the new interval can be placed. In other words, we need to skip all the intervals which end before the start of the new interval. So we can iterate through the given sorted listed of intervals and skip all the intervals with the following condition:

1	intervals[i].end < newInterval.start

Once we have found the correct place, we can follow an approach similar to Merge Intervals to insert and/or merge the new interval. Let’s call the new interval ‘a’ and the first interval with the above condition ‘b’. There are five possibilities:

The diagram above clearly shows the merging approach. To handle all four merging scenarios, we need to do something like this:

1 2	c.start = min(a.start, b.start) c.end = max(a.end, b.end)

Our overall algorithm will look like this:

Skip all intervals which end before the start of the new interval, i.e., skip all intervals with the following condition:

1	intervals[i].end < newInterval.start

Let’s call the last interval ‘b’ that does not satisfy the above condition. If ‘b’ overlaps with the new interval (a) (i.e. b.start <= a.end), we need to merge them into a new interval ‘c’:

1 2	c.start = min(a.start, b.start) c.end = max(a.end, b.end)

We will repeat the above two steps to merge ‘c’ with the next overlapping interval.

Code

Here is what our algorithm will look like:

#class Interval:
#  def __init__(self, start, end):
#    self.start = start
#    self.end = end

class Solution:
  def insert(self, intervals, new_interval):
    merged = []
    i = 0

    # skip (and add to output) all intervals that come before the 'new_interval'
    while i < len(intervals) and intervals[i].end < new_interval.start:
      merged.append(intervals[i])
      i += 1

    # merge all intervals that overlap with 'new_interval'
    while i < len(intervals) and intervals[i].start <= new_interval.end:
      new_interval.start = min(intervals[i].start, new_interval.start)
      new_interval.end = max(intervals[i].end, new_interval.end)
      i += 1

    # insert the new_interval
    merged.append(new_interval)

    # add all the remaining intervals to the output
    while i < len(intervals):
      merged.append(intervals[i])
      i += 1
    return merged

def print_interval(i):
  print("[" + str(i.start) + ", " + str(i.end) + "]", end='')

def main():
  sol = Solution()
  intervals = [Interval(1, 3), Interval(5, 7), Interval(8, 12)]
  print("Intervals after inserting the new interval: ",end="")
  for i in (sol.insert(intervals, Interval(4, 6))):
    print_interval(i)
  print()
  
  intervals = [Interval(1, 3), Interval(5, 7), Interval(8, 12)]
  print("Intervals after inserting the new interval: ",end="")
  for i in (sol.insert(intervals, Interval(4, 10))):
    print_interval(i)
  print()

  intervals = [Interval(2, 3), Interval(5, 7)]
  print("Intervals after inserting the new interval: ",end="")
  for i in (sol.insert(intervals, Interval(1, 4))):
    print_interval(i)
  print()
  
main()

Time complexity

As we are iterating through all the intervals only once, the time complexity of the above algorithm is O(N), where ‘N’ is the total number of intervals.

Space complexity

Ignoring the space needed for the result list, the algorithm runs in constant space O(1).

If we include the result list, the space complexity will be O(N) as we need to return a list containing all the merged intervals.

*Intervals Intersection (medium)

Top Interview 150 |986. Interval List Intersections Design Gurus Educative.io

Problem Statement

Given two lists of intervals, find the intersection of these two lists. Each list consists of disjoint intervals sorted on their start time.

Example 1:

1
2
3

Input: arr1=[[1, 3], [5, 6], [7, 9]], arr2=[[2, 3], [5, 7]]
Output: [2, 3], [5, 6], [7, 7]
Explanation: The output list contains the common intervals between the two lists.

Example 2:

1
2
3

Input: arr1=[[1, 3], [5, 7], [9, 12]], arr2=[[5, 10]]
Output: [5, 7], [9, 10]
Explanation: The output list contains the common intervals between the two lists.

Constraints:

0 <= arr1.length, arr2.length <= 1000
arr1.length + arr2.length >= 1
0 <= start_i < end_i <= 10^9
end_i < start_i+1
0 <= start_j < end_j <= 10^9
end_j < start_j+1

Solution

This problem follows the Merge Intervals pattern. As we have discussed under Insert Intervals, there are five overlapping possibilities between two intervals ‘a’ and ‘b’. A close observation will tell us that whenever the two intervals overlap, one of the interval’s start time lies within the other interval. This rule can help us identify if any two intervals overlap or not.

Now, if we have found that the two intervals overlap, how can we find the overlapped part?

Again from the above diagram, the overlapping interval will be equal to:

1 2	start = max(a.start, b.start) end = min(a.end, b.end)

That is, the highest start time and the lowest end time will be the overlapping interval.

So our algorithm will be to iterate through both the lists together to see if any two intervals overlap. If two intervals overlap, we will insert the overlapped part into a result list and move on to the next interval which is finishing early.

Code

Here is what our algorithm will look like:

#class Interval:
#  def __init__(self, start, end):
#    self.start = start
#    self.end = end

class Solution:
  def merge(self, intervals_a, intervals_b):
    result = []
    i, j, start, end = 0, 0, 0, 1

    while i < len(intervals_a) and j < len(intervals_b):
      # check if intervals overlap and intervals_a[i]'s start time lies within the 
      # other intervals_b[j]
      a_overlaps_b = intervals_a[i].start >= intervals_b[j].start and intervals_a[i].start <= intervals_b[j].end

      # check if intervals overlap and intervals_b[j]'s start time lies within the 
      # other intervals_a[i]
      b_overlaps_a = intervals_b[j].start >= intervals_a[i].start and intervals_b[j].start <= intervals_a[i].end

      # store the the intersection part
      if (a_overlaps_b or b_overlaps_a):
        result.append([max(intervals_a[i].start, intervals_b[j].start), min(
          intervals_a[i].end, intervals_b[j].end)])

      # move next from the interval which is finishing first
      if intervals_a[i].end < intervals_b[j].end:
        i += 1
      else:
        j += 1

    return result

def main():
  sol = Solution()
  intervals_a = [Interval(1, 3), Interval(5, 6), Interval(7, 9)]
  intervals_b = [Interval(2, 3), Interval(5, 7)]
  print("Intervals Intersection: ", end="")
  print(sol.merge(intervals_a,intervals_b))


  intervals_a = [Interval(1, 3), Interval(5, 7), Interval(9, 12)]
  intervals_b = [Interval(5, 10)]
  print("Intervals Intersection: ", end="")
  print(sol.merge(intervals_a,intervals_b))



main()

Time complexity

As we are iterating through both the lists once, the time complexity of the above algorithm is O(N+M), where ‘N’ and ‘M’ are the total number of intervals in the input arrays respectively.

Space complexity

Ignoring the space needed for the result list, the algorithm runs in constant space O(1).

Conflicting Appointments (medium)

Design Gurus Educative.io

Problem Statement

Given an array of intervals representing ‘N’ appointments, find out if a person can attend all the appointments.

Example 1:

1
2
3

Appointments: [[1,4], [2,5], [7,9]]
Output: false
Explanation: Since [1,4] and [2,5] overlap, a person cannot attend both of these appointments.

Example 2:

1
2
3

Appointments: [[6,7], [2,4], [8,12]]
Output: true
Explanation: None of the appointments overlap, therefore a person can attend all of them.

Example 3:

Appointments: [[4,5], [2,3], [3,6]]
Output: false
Explanation: Since [4,5] and [3,6] overlap, a person cannot attend both of these appointments.

Constraints:

1 <= intervals.length <= 10^4
intervals[i].length == 2
0 <= starti < endi <= 10^6

Solution

The problem follows the Merge Intervals pattern. We can sort all the intervals by start time and then check if any two intervals overlap. A person will not be able to attend all appointments if any two appointments overlap.

Code

Here is what our algorithm will look like:

#class Interval:
#  def __init__(self, start, end):
#    self.start = start
#    self.end = end

class Solution:
  def canAttendAllAppointments(self, intervals):
    intervals.sort(key=lambda x: x.start)
    for i in range(1, len(intervals)):
      # 注意这里是 < 不是 <=,因为<=还是可以参加所有的预约的
      if intervals[i].start < intervals[i-1].end:
        # please note the comparison above, it is "<" and not "<="
        # while merging we needed "<=" comparison, as we will be merging the two
        # intervals having condition "intervals[i][start] == intervals[i - 1][end]" but
        # such intervals don't represent conflicting appointments as one starts right
        # after the other
        return False
    return True


def main():
  sol = Solution()
  print("Can attend all appointments: " + 
            str(sol.canAttendAllAppointments([Interval(1, 4), Interval(2, 5), Interval(7, 9)])))
  print("Can attend all appointments: " + 
            str(sol.canAttendAllAppointments([Interval(6, 7), Interval(2, 4),Interval(8, 12)])))
  print("Can attend all appointments: " + 
            str(sol.canAttendAllAppointments([Interval(4, 5), Interval(2, 3), Interval(3, 6)])))


main()

Time complexity

The time complexity of the above algorithm is O(N\logN)*, where ‘N’ is the total number of appointments. Though we are iterating the intervals only once, our algorithm will take O(N\logN)* since we need to sort them in the beginning.

Space complexity

The space complexity of the above algorithm will be O(N), which we need for sorting. For Java, Arrays.sort() uses Timsort, which needs O(N) space.

*Problem Challenge 1

Design Gurus Educative.io

Minimum Meeting Rooms (hard)

Given a list of intervals representing the start and end time of ‘N’ meetings, find the minimum number of rooms required to hold all the meetings.

Example 1:

Meetings: [[1,4], [2,5], [7,9]]
Output: 2
Explanation: Since [1,4] and [2,5] overlap, we need two rooms to hold these two meetings. [7,9] can 
occur in any of the two rooms later.

Example 2:

1
2
3

Meetings: [[6,7], [2,4], [8,12]]
Output: 1
Explanation: None of the meetings overlap, therefore we only need one room to hold all meetings.

Example 3:

Meetings: [[1,4], [2,3], [3,6]]
Output:2
Explanation: Since [1,4] overlaps with the other two meetings [2,3] and [3,6], we need two rooms to 
hold all the meetings.

Example 4:

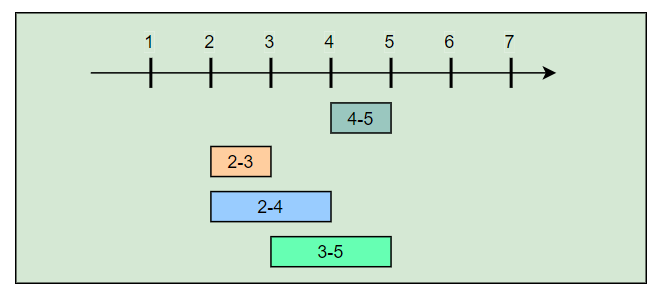
Meetings: [[4,5], [2,3], [2,4], [3,5]]
Output: 2
Explanation: We will need one room for [2,3] and [3,5], and another room for [2,4] and [4,5].
 
Here is a visual representation of Example 4:

Solution

Let’s take the above-mentioned example (4) and try to follow our Merge Intervals approach:

Meetings: [[4,5], [2,3], [2,4], [3,5]]

Step 1: Sorting these meetings on their start time will give us: [[2,3], [2,4], [3,5], [4,5]]

Step 2: Merging overlapping meetings:

[2,3] overlaps with [2,4], so after merging we’ll have => [[2,4], [3,5], [4,5]]
[2,4] overlaps with [3,5], so after merging we’ll have => [[2,5], [4,5]]
[2,5] overlaps [4,5], so after merging we’ll have => [2,5]

Since all the given meetings have merged into one big meeting ([2,5]), does this mean that they all are overlapping and we need a minimum of four rooms to hold these meetings? You might have already guessed that the answer is NO! As we can clearly see, some meetings are mutually exclusive. For example, [2,3] and [3,5] do not overlap and can happen in one room. So, to correctly solve our problem, we need to keep track of the mutual exclusiveness of the overlapping meetings.

Here is what our strategy will look like:

We will sort the meetings based on start time.
We will schedule the first meeting (let’s call it m1) in one room (let’s call it r1).
If the next meeting m2 is not overlapping with m1, we can safely schedule it in the same room r1.
If the next meeting m3 is overlapping with m2 we can’t use r1, so we will schedule it in another room (let’s call it r2).
Now if the next meeting m4 is overlapping with m3, we need to see if the room r1 has become free. For this, we need to keep track of the end time of the meeting happening in it. If the end time of m2 is before the start time of m4, we can use that room r1, otherwise, we need to schedule m4 in another room r3.

We can conclude that we need to keep track of the ending time of all the meetings currently happening so that when we try to schedule a new meeting, we can see what meetings have already ended. We need to put this information in a data structure that can easily give us the smallest ending time. A Min Heap would fit our requirements best.

So our algorithm will look like this:

Sort all the meetings on their start time.
Create a min-heap to store all the active meetings. This min-heap will also be used to find the active meeting with the smallest end time.
Iterate through all the meetings one by one to add them in the min-heap. Let’s say we are trying to schedule the meeting m1.
Since the min-heap contains all the active meetings, so before scheduling m1 we can remove all meetings from the heap that have ended before m1, i.e., remove all meetings from the heap that have an end time smaller than or equal to the start time of m1.
Now add m1 to the heap.
The heap will always have all the overlapping meetings, so we will need rooms for all of them. Keep a counter to remember the maximum size of the heap at any time which will be the minimum number of rooms needed.

Code

Here is what our algorithm will look like:

# 没有class的版本，一样能过。没有定义class，所以在使用heap的时候吧list的两个元素反转了一下
import heapq


class Solution:
    def findMinimumMeetingRooms(self, meetings):
        if not meetings:
            return 0

        # sort the meetings by start time
        meetings.sort(key=lambda x: x[0])

        minRooms = 0
        minHeap = []  # 按照end由小到大排列
        for meeting in meetings:
            # remove all meetings that have ended
            # 和最早的会议结束时间去比较，注意min_heap[0][0]是结束时间，因为在插入的时候
            while minHeap and meeting[0] >= minHeap[0][0]:
                heapq.heappop(minHeap)
            # add the current meeting into the minHeap
            heapq.heappush(minHeap, (meeting[1], meetings[0]))
            # all active meetings are in the minHeap, so we need rooms for all of them.
            minRooms = max(minRooms, len(minHeap))
        return minRooms


if __name__ == "__main__":
    sol = Solution()
    inputs = [
        [(1, 4), (2, 5), (7, 9)],
        [(6, 7), (2, 4), (8, 12)],
        [(1, 4), (2, 3), (3, 6)],
        [(4, 5), (2, 3), (2, 4), (3, 5)]
    ]

    for input in inputs:
        result = sol.findMinimumMeetingRooms(input)
        print("Minimum meeting rooms required:", result)

        
# 官方原版
import heapq

# class Meeting:
#     def __init__(self, start, end):
#         self.start = start
#         self.end = end
      

# You can override/modify __lt__ as per your need
setattr(Meeting, "__lt__", lambda self, other: self.end < other.end)

class Solution:
    def findMinimumMeetingRooms(self, meetings):
        if not meetings:
            return 0

        # sort the meetings by start time
        meetings.sort(key=lambda x: x.start)

        minRooms = 0
        minHeap = []
        for meeting in meetings:
            # remove all meetings that have ended
            while minHeap and meeting.start >= minHeap[0].end:
                heapq.heappop(minHeap)
            # add the current meeting into the minHeap
            heapq.heappush(minHeap, meeting)
            # all active meetings are in the minHeap, so we need rooms for all of them.
            minRooms = max(minRooms, len(minHeap))
        return minRooms

if __name__ == "__main__":
    sol = Solution()
    inputs = [
        [Meeting(1, 4), Meeting(2, 5), Meeting(7, 9)],
        [Meeting(6, 7), Meeting(2, 4), Meeting(8, 12)],
        [Meeting(1, 4), Meeting(2, 3), Meeting(3, 6)],
        [Meeting(4, 5), Meeting(2, 3), Meeting(2, 4), Meeting(3, 5)]
    ]

    for input in inputs:
        result = sol.findMinimumMeetingRooms(input)
        print("Minimum meeting rooms required:", result)

Time complexity

The time complexity of the above algorithm is O(N\logN)*, where ‘N’ is the total number of meetings. This is due to the sorting that we did in the beginning. Also, while iterating the meetings we might need to poll/offer meeting to the priority queue. Each of these operations can take O(N\logN)*. Overall our algorithm will take O(N\logN)*.

Space complexity

The space complexity of the above algorithm will be O(N) which is required for sorting. Also, in the worst case scenario, we’ll have to insert all the meetings into the Min Heap (when all meetings overlap) which will also take O(N) space. The overall space complexity of our algorithm is O(N).

Problem Challenge 2

Design Gurus Educative.io

Maximum CPU Load (hard)

We are given a list of Jobs. Each job has a Start time, an End time, and a CPU load when it is running. Our goal is to find the maximum CPU load at any time if all the jobs are running on the same machine.

Example 1:

Jobs: [[1,4,3], [2,5,4], [7,9,6]]
Output: 7
Explanation: Since [1,4,3] and [2,5,4] overlap, their maximum CPU load (3+4=7) will be when both the 
jobs are running at the same time i.e., during the time interval (2,4).

Example 2:

1
2
3

Jobs: [[6,7,10], [2,4,11], [8,12,15]]
Output: 15
Explanation: None of the jobs overlap, therefore we will take the maximum load of any job which is 15.

Example 3:

1
2
3

Jobs: [[1,4,2], [2,4,1], [3,6,5]]
Output: 8
Explanation: Maximum CPU load will be 8 as all jobs overlap during the time interval [3,4].

Solution

The problem follows the Merge Intervals pattern and can easily be converted to Minimum Meeting Rooms. Similar to ‘Minimum Meeting Rooms’ where we were trying to find the maximum number of meetings happening at any time, for ‘Maximum CPU Load’ we need to find the maximum number of jobs running at any time. We will need to keep a running count of the maximum CPU load at any time to find the overall maximum load.

Code

Here is what our algorithm will look like:

# 没有class的版本，一样能过。没有定义class，所以在使用heap的时候吧list的两个元素反转了一下
from heapq import *


class Solution:
    def findMaxCPULoad(self, jobs):
        # sort the jobs by start time
        jobs.sort(key=lambda x: x[0])
        max_cpu_load, current_cpu_load = 0, 0
        min_heap = []  # 需要按照job的end来由小到大排序

        for j in jobs:
            # remove all the jobs that have ended
            while min_heap and j[0] >= min_heap[0][0]:
                current_cpu_load -= min_heap[0][2]
                heappop(min_heap)
            # add the current job into min_heap
            heappush(min_heap, (j[1], j[0], j[2]))
            current_cpu_load += j[2]
            max_cpu_load = max(max_cpu_load, current_cpu_load)
        return max_cpu_load


def main():
    sol = Solution()
    print("Maximum CPU load at any time: " +
          str(sol.findMaxCPULoad([(1, 4, 3), (2, 5, 4), (7, 9, 6)])))
    print("Maximum CPU load at any time: " +
          str(sol.findMaxCPULoad([(6, 7, 10), (2, 4, 11), (8, 12, 15)])))
    print("Maximum CPU load at any time: " +
          str(sol.findMaxCPULoad([(1, 4, 2), (2, 4, 1), (3, 6, 5)])))


main()


# 官方版本
from heapq import *

#class job:
#  def __init__(self, start, end, cpu_load):
#    self.start = start
#    self.end = end
#    self.cpuLoad = cpu_load

# You can override/modify __lt__ as per your need
setattr(Job, "__lt__", lambda self, other: self.end < other.end)

class Solution:
  def findMaxCPULoad(self, jobs):
    # sort the jobs by start time
    jobs.sort(key=lambda x: x.start)
    max_cpu_load, current_cpu_load = 0, 0
    min_heap = []

    for j in jobs:
      # remove all the jobs that have ended
      while(len(min_heap) > 0 and j.start >= min_heap[0].end):
        current_cpu_load -= min_heap[0].cpuLoad
        heappop(min_heap)
      # add the current job into min_heap
      heappush(min_heap, j)
      current_cpu_load += j.cpuLoad
      max_cpu_load = max(max_cpu_load, current_cpu_load)
    return max_cpu_load


def main():
  sol = Solution()
  print("Maximum CPU load at any time: " + 
            str(sol.findMaxCPULoad([Job(1, 4, 3), Job(2, 5, 4), Job(7, 9, 6)])))
  print("Maximum CPU load at any time: " + 
            str(sol.findMaxCPULoad([Job(6, 7, 10), Job(2, 4, 11), Job(8, 12, 15)])))
  print("Maximum CPU load at any time: " + 
            str(sol.findMaxCPULoad([Job(1, 4, 2), Job(2, 4, 1), Job(3, 6, 5)])))

main()

Time complexity

The time complexity of the above algorithm is O(N\logN)*, where ‘N’ is the total number of jobs. This is due to the sorting that we did in the beginning. Also, while iterating the jobs, we might need to poll/offer jobs to the priority queue. Each of these operations can take O(log\N)*. Overall our algorithm will take O(N\logN)*

Space complexity

The space complexity of the above algorithm will be O(N), which is required for sorting. Also, in the worst case, we have to insert all the jobs into the priority queue (when all jobs overlap) which will also take O(N) space. The overall space complexity of our algorithm is O(N)

**Problem Challenge 3

Leetcode 会员 Design Gurus Educative.io

Employee Free Time (hard)

For ‘K’ employees, we are given a list of intervals representing the working hours of each employee. Our goal is to find out if there is a free interval that is common to all employees. You can assume that each list of employee working hours is sorted on the start time.

Example 1:

1
2
3

Input: Employee Working Hours=[[[1,3], [5,6]], [[2,3], [6,8]]]
Output: [3,5]
Explanation: Both the employess are free between [3,5].

Example 2:

1
2
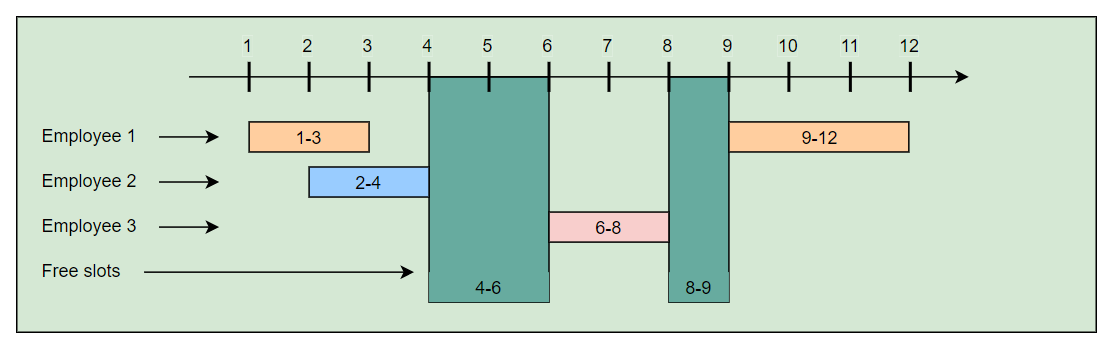
3

Input: Employee Working Hours=[[[1,3], [9,12]], [[2,4]], [[6,8]]]
Output: [4,6], [8,9]
Explanation: All employess are free between [4,6] and [8,9].

Example 3:

1
2
3

Input: Employee Working Hours=[[[1,3]], [[2,4]], [[3,5], [7,9]]]
Output: [5,7]
Explanation: All employess are free between [5,7].

Solution

This problem follows the Merge Intervals pattern.

Let’s take the above-mentioned example (2) and visually draw it:

1 2	Input: Employee Working Hours=[[[1,3], [9,12]], [[2,4]], [[6,8]]] Output: [4,6], [8,9]

One simple solution can be to put all employees’ working hours in a list and sort them on the start time. Then we can iterate through the list to find the gaps.（一开始我想的）

Let’s dig deeper.

Sorting the intervals of the above example will give us:

1	[1,3], [2,4], [6,8], [9,12]

We can now iterate through these intervals, and whenever we find non-overlapping intervals (e.g., [2,4] and [6,8]), we can calculate a free interval (e.g., [4,6]). This algorithm will take O(N \ logN)* time, where ‘N’ is the total number of intervals. This time is needed because we need to sort all the intervals. The space complexity will be O(N), which is needed for sorting. Can we find a better solution?

Using a Heap to Sort the Intervals

One fact that we are not utilizing is that each employee list is individually sorted!

How about we take the first interval of each employee and insert it in a Min Heap. This Min Heap can always give us the interval with the smallest start time. Once we have the smallest start-time interval, we can then compare it with the next smallest start-time interval (again from the Heap) to find the gap. This interval comparison is similar to what we suggested in the previous approach.

Whenever we take an interval out of the Min Heap, we can insert the next interval of the same employee. This also means that we need to know which interval belongs to which employee.

Code

Here is what our algorithm will look like:

大致可以看懂，但是定义EmplyeeInterval有点复杂了，可以直接使用三元组代替。

from heapq import *


# class Interval:
#    def __init__(self, start, end):
#        self.start = start
#        self.end = end

class EmployeeInterval:

    def __init__(self, interval, employeeIndex, intervalIndex):
        self.interval = interval  # interval representing employee's working hours
        # index of the list containing working hours of this employee
        self.employeeIndex = employeeIndex
        self.intervalIndex = intervalIndex  # index of the interval in the employee list

    def __lt__(self, other):
        # min heap based on meeting.start
        return self.interval.start < other.interval.start


class Solution:
    def findEmployeeFreeTime(self, schedule):
        if schedule is None:
            return []

        n = len(schedule)
        result, minHeap = [], []

        # insert the first interval of each employee to the queue
        for i in range(n):
            heappush(minHeap, EmployeeInterval(schedule[i][0], i, 0))

        previousInterval = minHeap[0].interval
        while minHeap:
            queueTop = heappop(minHeap)
            # if previousInterval is not overlapping with the next interval, insert a free 
            # interval
            if previousInterval.end < queueTop.interval.start:
                result.append(Interval(previousInterval.end,
                                       queueTop.interval.start))
                previousInterval = queueTop.interval
            else:  # overlapping intervals, update the previousInterval if needed
                if previousInterval.end < queueTop.interval.end:
                    previousInterval = queueTop.interval

            # if there are more intervals available for the same employee, add their next 
            # interval
            employeeSchedule = schedule[queueTop.employeeIndex]
            if len(employeeSchedule) > queueTop.intervalIndex + 1:
                heappush(minHeap, EmployeeInterval(
                    employeeSchedule[queueTop.intervalIndex + 1], queueTop.employeeIndex,
                    queueTop.intervalIndex + 1))

        return result


def print_interval(i):
    print("[" + str(i.start) + ", " + str(i.end) + "]", end='')


def main():
    sol = Solution()
    input = [[Interval(1, 3), Interval(5, 6)], [
        Interval(2, 3), Interval(6, 8)]]
    print("Free intervals: ", end='')
    for interval in sol.findEmployeeFreeTime(input):
        print_interval(interval)
    print()

    input = [[Interval(1, 3), Interval(9, 12)], [
        Interval(2, 4)], [Interval(6, 8)]]
    print("Free intervals: ", end='')
    for interval in sol.findEmployeeFreeTime(input):
        print_interval(interval)
    print()

    input = [[Interval(1, 3)], [
        Interval(2, 4)], [Interval(3, 5), Interval(7, 9)]]
    print("Free intervals: ", end='')
    for interval in sol.findEmployeeFreeTime(input):
        print_interval(interval)
    print()


main()

Time complexity

The time complexity of the above algorithm is O(N\logK)*, where ‘N’ is the total number of intervals and ‘K’ is the total number of employees. This is due to the fact that we are iterating through the intervals only once (which will take O(N)), and every time we process an interval, we remove (and can insert) one interval in the Min Heap, (which will take O(N\logK)*). At any time the heap will not have more than ‘K’ elements.

Space complexity

The space complexity of the above algorithm will be O(K) as at any time the heap will not have more than ‘K’ elements.

Author：Hasuer

Link：https://hasuer.github.io/4-pattern-merge-intervals/index.html

Publish date：May 4th 2024, 1:23:13 pm

Update date：May 28th 2024, 11:27:35 am

License：本文采用知识共享署名-非商业性使用 4.0 国际许可协议进行许可

Next Post

5. Pattern Cyclic Sort
Previous Post

3. Pattern Sliding Window

CATALOG

1. Introduction
2. *Merge Intervals (medium)
3. *Insert Interval (medium)
4. *Intervals Intersection (medium)
5. Conflicting Appointments (medium)
6. *Problem Challenge 1
7. Problem Challenge 2
8. **Problem Challenge 3

4. Pattern Merge Intervals

Introduction

*Merge Intervals (medium)

Problem Statement

Solution

Code

Time complexity

Space complexity

Similar Problems

*Insert Interval (medium)

Problem Statement

Solution

Code

Time complexity

Space complexity

*Intervals Intersection (medium)

Problem Statement

Solution

Code

Time complexity

Space complexity

Conflicting Appointments (medium)

Problem Statement

Solution

Code

Time complexity

Space complexity

Similar Problems

*Problem Challenge 1

Minimum Meeting Rooms (hard)

Solution

Code

Time complexity

Space complexity

Similar Problems

Problem Challenge 2

Maximum CPU Load (hard)

Solution

Code

Time complexity

Space complexity

**Problem Challenge 3

Employee Free Time (hard)

Solution

Using a Heap to Sort the Intervals

Code

Time complexity

Space complexity