Hasuer's Studio.

3. Pattern Sliding Window

Grokking Interview Pattern Interview
Word count: 6.9kReading time: 42 min
2024/05/03

Introduction

In many problems dealing with an array (or a LinkedList), we are asked to find or calculate something among all the contiguous subarrays (or sublists) of a given size. For example, take a look at this problem:

Given an array, find the average of all contiguous subarrays of size ‘K’ in it.

Let’s understand this problem with a real input:

1
Array: [1, 3, 2, 6, -1, 4, 1, 8, 2], K=5

Here, we are asked to find the average of all contiguous subarrays of size ‘5’ in the given array. Let’s solve this:

  1. For the first 5 numbers (subarray from index 0-4), the average is: (1+3+2+6-1)/5 => 2.2(1+3+2+6−1)/5=>2.2
  2. The average of next 5 numbers (subarray from index 1-5) is: (3+2+6-1+4)/5 => 2.8(3+2+6−1+4)/5=>2.8
  3. For the next 5 numbers (subarray from index 2-6), the average is: (2+6-1+4+1)/5 => 2.4(2+6−1+4+1)/5=>2.4
    …

Here is the final output containing the averages of all contiguous subarrays of size 5:

1
Output: [2.2, 2.8, 2.4, 3.6, 2.8]

A brute-force algorithm will be to calculate the sum of every 5-element contiguous subarray of the given array and divide the sum by ‘5’ to find the average. This is what the algorithm will look like:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution:
  def findAverages(self, K, arr):
    result = []
    for i in range(len(arr)-K+1):
      # find sum of next 'K' elements
      _sum = 0.0
      for j in range(i, i+K):
        _sum += arr[j]
      result.append(_sum/K)  # calculate average

    return result


def main():
  sol = Solution()
  result = sol.findAverages(5, [1, 3, 2, 6, -1, 4, 1, 8, 2])
  print("Averages of subarrays of size K: " + str(result))


main()

Time complexity: Since for every element of the input array, we are calculating the sum of its next ‘K’ elements, the time complexity of the above algorithm will be O(N\K)* where ‘N’ is the number of elements in the input array.

Can we find a better solution? Do you see any inefficiency in the above approach?

The inefficiency is that for any two consecutive subarrays of size ‘5’, the overlapping part (which will contain four elements) will be evaluated twice. For example, take the above-mentioned input:

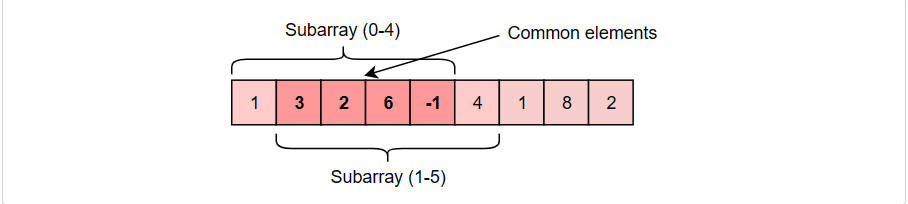
As you can see, there are four overlapping elements between the subarray (indexed from 0-4) and the subarray (indexed from 1-5). Can we somehow reuse the sum we have calculated for the overlapping elements?

The efficient way to solve this problem would be to visualize each contiguous subarray as a sliding window of ‘5’ elements. This means that when we move on to the next subarray, we will slide the window by one element. So, to reuse the sum from the previous subarray, we will subtract the element going out of the window and add the element now being included in the sliding window. This will save us from going through the whole subarray to find the sum and, as a result, the algorithm complexity will reduce to O(N).

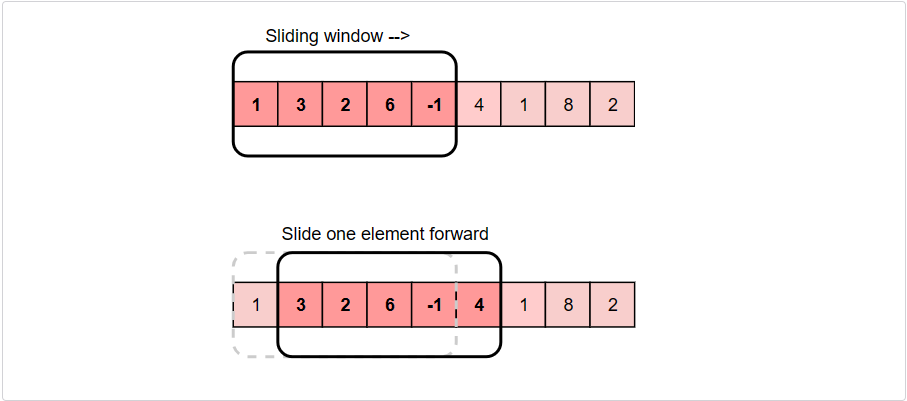
Here is the algorithm for the Sliding Window approach:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution:
  def findAverages(self, K, arr):
      result = []
      windowSum, windowStart = 0.0, 0
      for windowEnd in range(len(arr)):
          windowSum += arr[windowEnd]  # add the next element
          # slide the window, no need to slide if we've not hit the required window size of 'k'
          if windowEnd >= K - 1:
              result.append(windowSum / K)  # calculate the average
              windowSum -= arr[windowStart]  # subtract the element going out
              windowStart += 1  # slide the window ahead

      return result


def main():
  sol = Solution()
  result = sol.findAverages(5, [1, 3, 2, 6, -1, 4, 1, 8, 2])
  print("Averages of subarrays of size K: " + str(result))


main()

In the following chapters, we will apply the Sliding Window approach to solve a few problems.

In some problems, the size of the sliding window is not fixed. We have to expand or shrink the window based on the problem constraints. We will see a few examples of such problems in the next chapters.

Let’s jump onto our first problem and apply the Sliding Window pattern.

Maximum Sum Subarray of Size K (easy)

Design Gurus Educative.io

Problem Statement

Given an array of positive numbers and a positive number ‘k’, find the maximum sum of any contiguous subarray of size ‘k’.

Example 1:

1
2
3
Input: [2, 1, 5, 1, 3, 2], k=3 
Output: 9
Explanation: Subarray with maximum sum is [5, 1, 3].

Example 2:

1
2
3
Input: [2, 3, 4, 1, 5], k=2 
Output: 7
Explanation: Subarray with maximum sum is [3, 4].

Solution

A basic brute force solution will be to calculate the sum of all ‘k’ sized subarrays of the given array to find the subarray with the highest sum. We can start from every index of the given array and add the next ‘k’ elements to find the subarray’s sum. Following is the visual representation of this algorithm for Example-1:

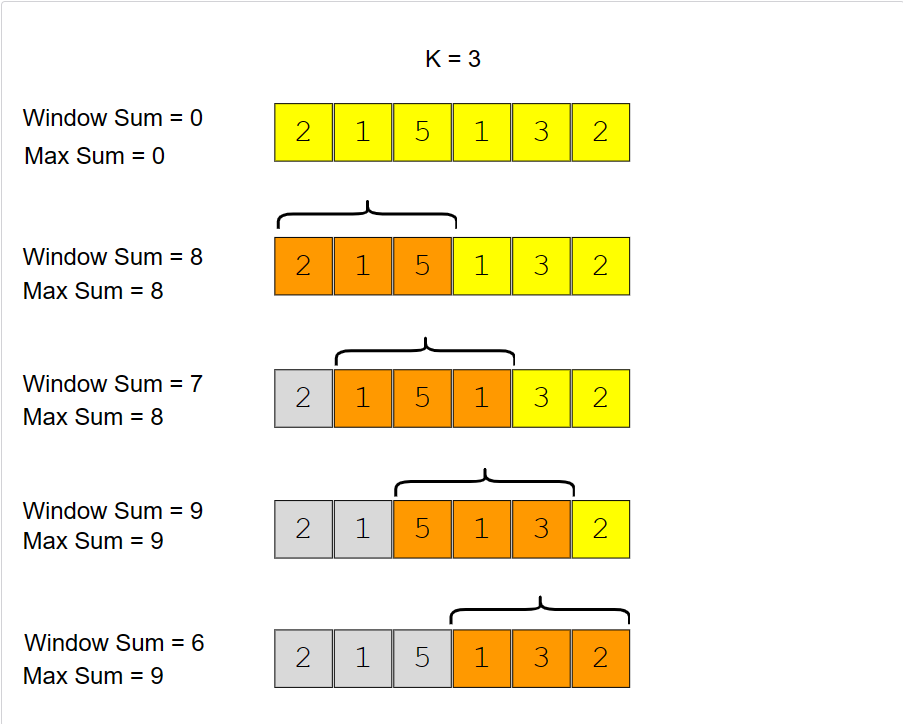
Code

Here is what our algorithm will look like:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution:
    def findMaxSumSubArray(self, k, arr):
        max_sum, window_sum = 0, 0
        window_start = 0

        for window_end in range(len(arr)):
            window_sum += arr[window_end]  # add the next element
            # slide the window, no need to slide if we've not hit the required window size of 'k'
            if window_end >= k-1:
                max_sum = max(max_sum, window_sum)
                window_sum -= arr[window_start]  # subtract the element going out
                window_start += 1  # slide the window ahead
        return max_sum

def main():
    sol = Solution()
    print("Maximum sum of a subarray of size K: " +
        str(sol.findMaxSumSubArray(3, [2, 1, 5, 1, 3, 2])))
    print("Maximum sum of a subarray of size K: " +
        str(sol.findMaxSumSubArray(2, [2, 3, 4, 1, 5])))


main()

Time Complexity

The time complexity of the above algorithm will be O(N).

Space Complexity

The algorithm runs in constant space O(1).

Smallest Subarray with a given sum (easy)

Top Interview 150 | 209. Minimum Size Subarray Sum Design Gurus Educative.io

Problem Statement

Given an array of positive numbers and a positive number ‘S’, find the length of the smallest contiguous subarray whose sum is greater than or equal to ‘S’. Return 0, if no such subarray exists.

Example 1:

1
2
3
Input: [2, 1, 5, 2, 3, 2], S=7 
Output: 2
Explanation: The smallest subarray with a sum great than or equal to '7' is [5, 2].

Example 2:

1
2
3
Input: [2, 1, 5, 2, 8], S=7 
Output: 1
Explanation: The smallest subarray with a sum greater than or equal to '7' is [8].

Example 3:

1
2
3
Input: [3, 4, 1, 1, 6], S=8 
Output: 3
Explanation: Smallest subarrays with a sum greater than or equal to '8' are [3, 4, 1] or [1, 1, 6].

Constraints:

  • 1 <= S <= 10^9
  • 1 <= arr.length <= 10^5
  • 1 <= arr[i] <= 10^4

Solution

This problem follows the Sliding Window pattern and we can use a similar strategy as discussed in Maximum Sum Subarray of Size K. There is one difference though: in this problem, the size of the sliding window is not fixed. Here is how we will solve this problem:

  1. First, we will add-up elements from the beginning of the array until their sum becomes greater than or equal to ‘S’.
  2. These elements will constitute our sliding window. We are asked to find the smallest such window having a sum greater than or equal to ‘S’. We will remember the length of this window as the smallest window so far.
  3. After this, we will keep adding one element in the sliding window (i.e. slide the window ahead), in a stepwise fashion.
  4. In each step, we will also try to shrink the window from the beginning. We will shrink the window until the window’s sum is smaller than ‘S’ again. This is needed as we intend to find the smallest window. This shrinking will also happen in multiple steps; in each step we will do two things:
    • Check if the current window length is the smallest so far, and if so, remember its length.
    • Subtract the first element of the window from the running sum to shrink the sliding window.

Here is the visual representation of this algorithm for the Example-1:

Code

Here is what our algorithm will look:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
import math

class Solution:
    def findMinSubArray(self, s, arr):
        window_sum = 0      # Initialize the sum of the current window
        min_length = math.inf  # Initialize the minimum length to positive infinity
        window_start = 0    # Initialize the start of the current window

        for window_end in range(0, len(arr)):
            window_sum += arr[window_end]  # Add the next element to the window sum
            # Shrink the window as small as possible until 'window_sum' is smaller than 's'
            while window_sum >= s:
                min_length = min(min_length, window_end - window_start + 1)  # Update the minimum length
                window_sum -= arr[window_start]  # Remove the element going out of the window
                window_start += 1  # Slide the window ahead
        
        if min_length == math.inf:
            return 0
        return min_length


def main():
    sol = Solution()
    print("Smallest subarray length: " + str(sol.findMinSubArray(7, [2, 1, 5, 2, 3, 2])))
    print("Smallest subarray length: " + str(sol.findMinSubArray(7, [2, 1, 5, 2, 8])))
    print("Smallest subarray length: " + str(sol.findMinSubArray(8, [3, 4, 1, 1, 6])))

main()

Time Complexity

The time complexity of the above algorithm will be O(N). The outer for loop runs for all elements and the inner while loop processes each element only once, therefore the time complexity of the algorithm will be O(N+N) which is asymptotically equivalent to O(N).

Space Complexity

The algorithm runs in constant space O(1).

Longest Substring with K Distinct Characters (medium)

Design Gurus Educative.io

Problem Statement

Given a string, find the length of the longest substring in it with no more than K distinct characters.

You can assume that K is less than or equal to the length of the given string.

Example 1:

1
2
3
Input: String="araaci", K=2
Output: 4
Explanation: The longest substring with no more than '2' distinct characters is "araa".

Example 2:

1
2
3
Input: String="araaci", K=1
Output: 2
Explanation: The longest substring with no more than '1' distinct characters is "aa".

Example 3:

1
2
3
Input: String="cbbebi", K=3
Output: 5
Explanation: The longest substrings with no more than '3' distinct characters are "cbbeb" & "bbebi".

Constraints:

  • 1 <= str.length <= 5 * 104
  • 0 <= K <= 50

Solution

This problem follows the Sliding Window pattern and we can use a similar dynamic sliding window strategy as discussed in Smallest Subarray with a given sum. We can use a HashMap to remember the frequency of each character we have processed. Here is how we will solve this problem:

  1. First, we will insert characters from the beginning of the string until we have ‘K’ distinct characters in the HashMap.
  2. These characters will constitute our sliding window. We are asked to find the longest such window having no more than ‘K’ distinct characters. We will remember the length of this window as the longest window so far.
  3. After this, we will keep adding one character in the sliding window (i.e. slide the window ahead), in a stepwise fashion.
  4. In each step, we will try to shrink the window from the beginning if the count of distinct characters in the HashMap is larger than ‘K’. We will shrink the window until we have no more than ‘K’ distinct characters in the HashMap. This is needed as we intend to find the longest window.
  5. While shrinking, we’ll decrement the frequency of the character going out of the window and remove it from the HashMap if its frequency becomes zero.
  6. At the end of each step, we’ll check if the current window length is the longest so far, and if so, remember its length.

Here is the visual representation of this algorithm for the Example-1:

Code

Here is how our algorithm will look:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
class Solution:
    def findLength(self, str1, k):
        window_start = 0
        max_length = 0
        char_frequency = {}

        # in the following loop we'll try to extend the range [window_start, window_end]
        for window_end in range(len(str1)):
            right_char = str1[window_end]
            if right_char not in char_frequency:
                char_frequency[right_char] = 0
            char_frequency[right_char] += 1

            # shrink the sliding window, until we are left with 'k' distinct characters in
            # the char_frequency
            while len(char_frequency) > k:
                left_char = str1[window_start]
                char_frequency[left_char] -= 1
                if char_frequency[left_char] == 0:
                    del char_frequency[left_char]
                window_start += 1  # shrink the window
            # remember the maximum length so far
            max_length = max(max_length, window_end-window_start + 1)
        return max_length


def main():
    sol = Solution()
    print("Length of the longest substring: "
          + str(sol.findLength("araaci", 2)))
    print("Length of the longest substring: "
          + str(sol.findLength("araaci", 1)))
    print("Length of the longest substring: "
          + str(sol.findLength("cbbebi", 3)))


main()

Time Complexity

The time complexity of the above algorithm will be O(N) where ‘N’ is the number of characters in the input string. The outer for loop runs for all characters and the inner while loop processes each character only once, therefore the time complexity of the algorithm will be O(N+N)O(N+N) which is asymptotically equivalent to O(N).

Space Complexity

The space complexity of the algorithm is O(K), as we will be storing a maximum of ‘K+1’ characters in the HashMap.

Fruits into Baskets (medium)

904. Fruit Into Baskets Design Gurus Educative.io

You are visiting a farm to collect fruits. The farm has a single row of fruit trees. You will be given two baskets, and your goal is to pick as many fruits as possible to be placed in the given baskets.

You will be given an array of characters where each character represents a fruit tree. The farm has following restrictions:

  1. Each basket can have only one type of fruit. There is no limit to how many fruit a basket can hold.
  2. You can start with any tree, but you can’t skip a tree once you have started.
  3. You will pick exactly one fruit from every tree until you cannot, i.e., you will stop when you have to pick from a third fruit type.

Write a function to return the maximum number of fruits in both baskets.

Example 1:

1
2
3
Input: arr=['A', 'B', 'C', 'A', 'C']  
Output: 3  
Explanation: We can put 2 'C' in one basket and one 'A' in the other from the subarray ['C', 'A', 'C']

Example 2:

1
2
3
Input: arr = ['A', 'B', 'C', 'B', 'B', 'C']  
Output: 5  
Explanation: We can put 3 'B' in one basket and two 'C' in the other basket. This can be done if we start with the second letter: ['B', 'C', 'B', 'B', 'C']

Constraints:

  • 1 <= arr.length <= 10^5
  • 0 <= arr[i] < arr.length

Solution

This problem follows the Sliding Window pattern and is quite similar to Longest Substring with K Distinct Characters. In this problem, we need to find the length of the longest subarray with no more than two distinct characters (or fruit types!). This transforms the current problem into Longest Substring with K Distinct Characters where K=2.

Code

Here is what our algorithm will look like, only the highlighted lines are different from Longest Substring with K Distinct Characters

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class Solution:
    def findLength(self, fruits):
        window_start = 0
        max_length = 0
        fruit_frequency = {}

        # try to extend the range [window_start, window_end]
        for window_end in range(len(fruits)):
            right_fruit = fruits[window_end]
            if right_fruit not in fruit_frequency:
                fruit_frequency[right_fruit] = 0
            fruit_frequency[right_fruit] += 1

            # shrink the sliding window, until we are left with '2' fruits in the fruit
            # frequency dictionary
            while len(fruit_frequency) > 2:
                left_fruit = fruits[window_start]
                fruit_frequency[left_fruit] -= 1
                if fruit_frequency[left_fruit] == 0:
                    del fruit_frequency[left_fruit]
                window_start += 1  # shrink the window
            max_length = max(max_length, window_end-window_start + 1)
        return max_length


def main():
    sol = Solution()
    print("Maximum number of fruits: "
          + str(sol.findLength(['A', 'B', 'C', 'A', 'C'])))
    print("Maximum number of fruits: "
          + str(sol.findLength(['A', 'B', 'C', 'B', 'B', 'C'])))


main()

Time Complexity

The time complexity of the above algorithm will be O(N) where ‘N’ is the number of characters in the input array. The outer for loop runs for all characters and the inner while loop processes each character only once, therefore the time complexity of the algorithm will be O(N+N)O(N+N) which is asymptotically equivalent to O(N).

Space Complexity

The algorithm runs in constant space O(1) as there can be a maximum of three types of fruits stored in the frequency map.

Similar Problems

Problem 1: Longest Substring with at most 2 distinct characters

Given a string, find the length of the longest substring in it with at most two distinct characters.

Solution: This problem is exactly similar to our parent problem.

No-repeat Substring (hard)

Top Interview 150 | 3. Longest Substring Without Repeating Characters Educative.io

Problem Statement

Given a string, find the length of the longest substring which has no repeating characters.

Example 1:

1
2
3
Input: String="aabccbb"
Output: 3
Explanation: The longest substring without any repeating characters is "abc".

Example 2:

1
2
3
Input: String="abbbb"
Output: 2
Explanation: The longest substring without any repeating characters is "ab".

Example 3:

1
2
3
Input: String="abccde"
Output: 3
Explanation: Longest substrings without any repeating characters are "abc" & "cde".

Solution

This problem follows the Sliding Window pattern and we can use a similar dynamic sliding window strategy as discussed in Longest Substring with K Distinct Characters. We can use a HashMap to remember the last index of each character we have processed. Whenever we get a repeating character we will shrink our sliding window to ensure that we always have distinct characters in the sliding window.

Code

Here is what our algorithm will look like:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
def non_repeat_substring(str):
    start = 0
    max_length = 0
    char_index_map = {}
    for end in range(len(str)):
        right_char = str[end]
        if  right_char in  char_index_map:
            left_char = str[start]
            start = max(start, char_index_map[right_char] + 1)
        char_index_map[right_char] = end
        max_length = max(max_length, end - start + 1)
    return max_length


def main():
    result = non_repeat_substring("aabccbb")
    print("Result: " + str(result))
    result = non_repeat_substring("abbb")
    print("Result: " + str(result))
    result = non_repeat_substring("abccde")
    print("Result: " + str(result))


if __name__ == '__main__':
    main()

Time Complexity

The time complexity of the above algorithm will be O(N) where ‘N’ is the number of characters in the input string.

Space Complexity

The space complexity of the algorithm will be O(K) where KK is the number of distinct characters in the input string. This also means K<=N, because in the worst case, the whole string might not have any repeating character so the entire string will be added to the HashMap. Having said that, since we can expect a fixed set of characters in the input string (e.g., 26 for English letters), we can say that the algorithm runs in fixed space O(1); in this case, we can use a fixed-size array instead of the HashMap.

*Longest Substring with Same Letters after Replacement (hard)

424. Longest Repeating Character Replacement Design Gurus Educative.io

Problem Statement

Given a string with lowercase letters only, if you are allowed to replace no more than ‘k’ letters with any letter, find the length of the longest substring having the same letters after replacement.

Example 1:

1
2
3
Input: String="aabccbb", k=2
Output: 5
Explanation: Replace the two 'c' with 'b' to have a longest repeating substring "bbbbb".

Example 2:

1
2
3
Input: String="abbcb", k=1
Output: 4
Explanation: Replace the 'c' with 'b' to have a longest repeating substring "bbbb".

Example 3:

1
2
3
Input: String="abccde", k=1
Output: 3
Explanation: Replace the 'b' or 'd' with 'c' to have the longest repeating substring "ccc".

Constraints:

  • 1 <= str.length <= 10^5
  • s consists of only lowercase English letters.
  • 0 <= k <= s.length

Solution

This problem follows the Sliding Window pattern, and we can use a similar dynamic sliding window strategy as discussed in Longest Substring with Distinct Characters. We can use a HashMap to count the frequency of each letter.

  1. We will iterate through the string to add one letter at a time in the window.

  2. We will also keep track of the count of the maximum repeating letter in any window (let’s call it maxRepeatLetterCount).

  3. So, at any time, we know that we do have a window with one letter repeating maxRepeatLetterCount

    times; this means we should try to replace the remaining letters.

    1. If the remaining letters are less than or equal to ‘k’, we can replace them all.
    2. If we have more than ‘k’ remaining letters, we should shrink the window as we cannot replace more than ‘k’ letters.

While shrinking the window, we don’t need to update maxRepeatLetterCount. Since we are only interested in the longest valid substring, our sliding windows do not have to shrink, even if a window may cover an invalid substring. Either we expand the window by appending a character to the right or we shift the entire window to the right by one. We only expand the window when the frequency of the newly added character exceeds the historical maximum frequency (from a previous window that included a valid substring). In other words, we do not need to know the exact maximum count of the current window. The only thing we need to know is whether the maximum count exceeds the historical maximum count, and that can only happen because of the newly added char.

Code

Here is what our algorithm will look like:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
class Solution:
    def findLength(self, str1, k):
        window_start, max_length, max_repeat_letter_count = 0, 0, 0
        frequency_map = {}

        # Try to extend the range [window_start, window_end]
        for window_end in range(len(str1)):
            right_char = str1[window_end]
            if right_char not in frequency_map:
                frequency_map[right_char] = 0
            frequency_map[right_char] += 1

            # we don't need to place the maxRepeatLetterCount under the below 'if', see the
            # explanation in the 'Solution' section above.
            # 也可以使用max(char_frequency.values())，还是感觉这个好理解一点
            max_repeat_letter_count = max(
                max_repeat_letter_count, frequency_map[right_char])

            # Current window size is from window_start to window_end, overall we have a letter
            # which is repeating 'max_repeat_letter_count' times, this means we can have a window
            # which has one letter repeating 'max_repeat_letter_count' times and the remaining
            # letters we should replace. If the remaining letters are more than 'k', it is the
            # time to shrink the window as we are not allowed to replace more than 'k' letters
            # 这里也可以用while，但是看solution的说法
            if (window_end - window_start + 1 - max_repeat_letter_count) > k:
                left_char = str1[window_start]
                frequency_map[left_char] -= 1
                window_start += 1

            max_length = max(max_length, window_end - window_start + 1)
        return max_length


def main():
    sol = Solution()
    print(sol.findLength("aabccbb", 2))
    print(sol.findLength("abbcb", 1))
    print(sol.findLength("abccde", 1))


main()


Time Complexity

The time complexity of the above algorithm will be O(N) where ‘N’ is the number of letters in the input string.

Space Complexity

As we are expecting only the lower case letters in the input string, we can conclude that the space complexity will be O(26), to store each letter’s frequency in the HashMap, which is asymptotically equal to O(1).

Longest Subarray with Ones after Replacement (hard)

1004. Max Consecutive Ones III Design Gurus Educative.io

Problem Statement

Given an array containing 0s and 1s, if you are allowed to replace no more than ‘k’ 0s with 1s, find the length of the longest contiguous subarray having all 1s.

Example 1:

1
2
3
Input: Array=[0, 1, 1, 0, 0, 0, 1, 1, 0, 1, 1], k=2
Output: 6
Explanation: Replace the '0' at index 5 and 8 to have the longest contiguous subarray of 1s having length 6.

Example 2:

1
2
3
Input: Array=[0, 1, 0, 0, 1, 1, 0, 1, 1, 0, 0, 1, 1], k=3
Output: 9
Explanation: Replace the '0' at index 6, 9, and 10 to have the longest contiguous subarray of 1s having length 9.

Constraints:

  • 1 <= arr.length <= 10^5
  • arr[i] is either 0 or 1.
  • 0 <= k <= nums.length

Solution

This problem follows the Sliding Window pattern and is quite similar to Longest Substring with same Letters after Replacement. The only difference is that, in the problem, we only have two characters (1s and 0s) in the input arrays.

Following a similar approach, we’ll iterate through the array to add one number at a time in the window. We’ll also keep track of the maximum number of repeating 1s in the current window (let’s call it maxOnesCount). So at any time, we know that we can have a window with 1s repeating maxOnesCount time, so we should try to replace the remaining 0s. If we have more than ‘k’ remaining 0s, we should shrink the window as we are not allowed to replace more than ‘k’ 0s.

Code

Here is how our algorithm will look like:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution:
    def findLength(self, arr, k):
        window_start, max_length, max_ones_count = 0, 0, 0

        # Try to extend the range [window_start, window_end]
        for window_end in range(len(arr)):
            if arr[window_end] == 1:
                max_ones_count += 1

            # Current window size is from window_start to window_end, overall we have a maximum
            # of 1s repeating 'max_ones_count' times, this means we can have a window with
            # 'max_ones_count' 1s and the remaining are 0s which should replace with 1s.
            # Now, if the remaining 0s are more than 'k', it is the time to shrink the window as
            # we are not allowed to replace more than 'k' 0s
            if (window_end - window_start + 1 - max_ones_count) > k:
                if arr[window_start] == 1:
                    max_ones_count -= 1
                window_start += 1

            max_length = max(max_length, window_end - window_start + 1)
        return max_length


def main():
    sol = Solution()
    print(sol.findLength([0, 1, 1, 0, 0, 0, 1, 1, 0, 1, 1], 2))
    print(sol.findLength([0, 1, 0, 0, 1, 1, 0, 1, 1, 0, 0, 1, 1], 3))


main()

Time Complexity

The time complexity of the above algorithm will be O(N) where ‘N’ is the count of numbers in the input array.

Space Complexity

The algorithm runs in constant space O(1).

*Problem Challenge 1

567. Permutation in String Design Gurus Educative.io

Permutation in a String (hard)

Given a string and a pattern, find out if the string contains any permutation of the pattern.

Permutation is defined as the re-arranging of the characters of the string. For example, “abc” has the following six permutations:

  1. abc
  2. acb
  3. bac
  4. bca
  5. cab
  6. cba

If a string has ‘n’ distinct characters it will have n! permutations.

Example 1:

1
2
3
Input: String="oidbcaf", Pattern="abc"
Output: true
Explanation: The string contains "bca" which is a permutation of the given pattern.

Example 2:

1
2
3
Input: String="odicf", Pattern="dc"
Output: false
Explanation: No permutation of the pattern is present in the given string as a substring.

Example 3:

1
2
3
Input: String="bcdxabcdy", Pattern="bcdyabcdx"
Output: true
Explanation: Both the string and the pattern are a permutation of each other.

Example 4:

1
2
3
Input: String="aaacb", Pattern="abc"
Output: true
Explanation: The string contains "acb" which is a permutation of the given pattern.

Constraints:

  • 1 <= str.length, pat.length <= 104
  • str and pat consist of lowercase English letters.

Solution

This problem follows the Sliding Window pattern and we can use a similar sliding window strategy as discussed in Longest Substring with K Distinct Characters. We can use a HashMap to remember the frequencies of all characters in the given pattern. Our goal will be to match all the characters from this HashMap with a sliding window in the given string. Here are the steps of our algorithm:

  1. Create a HashMap to calculate the frequencies of all characters in the pattern.
  2. Iterate through the string, adding one character at a time in the sliding window.
  3. If the character being added matches a character in the HashMap, decrement its frequency in the map. If the character frequency becomes zero, we got a complete match.
  4. If at any time, the number of characters matched is equal to the number of distinct characters in the pattern (i.e., total characters in the HashMap), we have gotten our required permutation.
  5. If the window size is greater than the length of the pattern, shrink the window to make it equal to the size of the pattern. At the same time, if the character going out was part of the pattern, put it back in the frequency HashMap.

Code

Here is what our algorithm will look like:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
class Solution:
    def findPermutation(self, str1, pattern):
        window_start, matched = 0, 0
        char_frequency = {}

        for chr in pattern:
            if chr not in char_frequency:
                char_frequency[chr] = 0
            char_frequency[chr] += 1

        # our goal is to match all the characters from the 'char_frequency' with the current
        # window try to extend the range [window_start, window_end]
        for window_end in range(len(str1)):
            right_char = str1[window_end]
            if right_char in char_frequency:
                # decrement the frequency of matched character
                char_frequency[right_char] -= 1
                if char_frequency[right_char] == 0:
                    matched += 1
			# 这里的if也是可以缩进的，leetcode过了
            if matched == len(char_frequency):
                return True

            # shrink the window by one character
            if window_end >= len(pattern) - 1:
                left_char = str1[window_start]
                window_start += 1
                if left_char in char_frequency:
                    if char_frequency[left_char] == 0:
                        matched -= 1
                    char_frequency[left_char] += 1

        return False


def main():
    sol = Solution()
    print('Permutation exist: ' + str(sol.findPermutation("oidbcaf", "abc")))
    print('Permutation exist: ' + str(sol.findPermutation("odicf", "dc")))
    print('Permutation exist: ' + str(sol.findPermutation("bcdxabcdy", "bcdyabcdx")))
    print('Permutation exist: ' + str(sol.findPermutation("aaacb", "abc")))


main()

Time Complexity

The time complexity of the above algorithm will be O(N + M) where ‘N’ and ‘M’ are the number of characters in the input string and the pattern respectively.

Space Complexity

The space complexity of the algorithm is O(M) since in the worst case, the whole pattern can have distinct characters which will go into the HashMap.

Problem Challenge 2

438. Find All Anagrams in a String Design Gurus Educative.io

String Anagrams (hard)

Given a string and a pattern, find all anagrams of the pattern in the given string.

Anagram is actually a Permutation of a string. For example, “abc” has the following six anagrams:

  1. abc
  2. acb
  3. bac
  4. bca
  5. cab
  6. cba

Write a function to return a list of starting indices of the anagrams of the pattern in the given string.

Example 1:

1
2
3
Input: String="ppqp", Pattern="pq"
Output: [1, 2]
Explanation: The two anagrams of the pattern in the given string are "pq" and "qp".

Example 2:

1
2
3
Input: String="abbcabc", Pattern="abc"
Output: [2, 3, 4]
Explanation: The three anagrams of the pattern in the given string are "bca", "cab", and "abc".

Constraints:

  • 1 <= s.length, p.length <= 3 * 10^4
  • str and pattern consist of lowercase English letters.

Solution

This problem follows the Sliding Window pattern and is very similar to Permutation in a String. In this problem, we need to find every occurrence of any permutation of the pattern in the string. We will use a list to store the starting indices of the anagrams of the pattern in the string.

Code

Here is what our algorithm will look like, only the highlighted lines have changed from Permutation in a String:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
class Solution:
    def findStringAnagrams(self, str1, pattern):
        window_start, matched = 0, 0
        char_frequency = {}

        for chr in pattern:
            if chr not in char_frequency:
                char_frequency[chr] = 0
            char_frequency[chr] += 1

        result_indices = []
        # Our goal is to match all the characters from the 'char_frequency' with the current
        # window try to extend the range [window_start, window_end]
        for window_end in range(len(str1)):
            right_char = str1[window_end]
            if right_char in char_frequency:
                # Decrement the frequency of matched character
                char_frequency[right_char] -= 1
                if char_frequency[right_char] == 0:
                    matched += 1

            if matched == len(char_frequency):  # Have we found an anagram?
                result_indices.append(window_start)

            # Shrink the sliding window
            if window_end >= len(pattern) - 1:
                left_char = str1[window_start]
                window_start += 1
                if left_char in char_frequency:
                    if char_frequency[left_char] == 0:
                        matched -= 1  # Before putting the character back, decrement the matched count
                    char_frequency[left_char] += 1  # Put the character back

        return result_indices


def main():
    sol = Solution()
    print(sol.findStringAnagrams("ppqp", "pq"))
    print(sol.findStringAnagrams("abbcabc", "abc"))


main()

Time Complexity

The time complexity of the above algorithm will be O(N + M) where ‘N’ and ‘M’ are the number of characters in the input string and the pattern respectively.

Space Complexity

The space complexity of the algorithm is O(M) since in the worst case, the whole pattern can have distinct characters which will go into the HashMap. In the worst case, we also need O(N) space for the result list, this will happen when the pattern has only one character and the string contains only that character.

Problem Challenge 3

Top Interview 150 | 76. Minimum Window Substring Design Gurus Educative.io

Smallest Window containing Substring (hard)

Given a string and a pattern, find the smallest substring in the given string which has all the characters of the given pattern.

Example 1:

1
2
3
Input: String="aabdec", Pattern="abc"  
Output: "abdec"  
Explanation: The smallest substring having all characters of the pattern is "abdec"

Example 2:

1
2
3
Input: String="aabdec", Pattern="abac"  
Output: "aabdec"  
Explanation: The smallest substring having all characters occurrences of the pattern is "aabdec"

Example 3:

1
2
3
Input: String="abdbca", Pattern="abc"  
Output: "bca"  
Explanation: The smallest substring having all characters of the pattern is "bca".

Example 4:

1
2
3
Input: String="adcad", Pattern="abc"  
Output: ""  
Explanation: No substring in the given string has all characters of the pattern

Constraints:

  • m == String.length
  • n == Pattern.length
  • 1 <= m, n <= 10^5
  • String and Pattern consist of uppercase and lowercase English letters.

Solution

This problem follows the Sliding Window pattern and has a lot of similarities with Permutation in a String with one difference. In this problem, we need to find a substring having all characters of the pattern which means that the required substring can have some additional characters and doesn’t need to be a permutation of the pattern. Here is how we will manage these differences:

  1. We will keep a running count of every matching instance of a character.
  2. Whenever we have matched all the characters, we will try to shrink the window from the beginning, keeping track of the smallest substring that has all the matching characters.
  3. We will stop the shrinking process as soon as we remove a matched character from the sliding window. One thing to note here is that we could have redundant matching characters, e.g., we might have two ‘a’ in the sliding window when we only need one ‘a’. In that case, when we encounter the first ‘a’, we will simply shrink the window without decrementing the matched count. We will decrement the matched count when the second ‘a’ goes out of the window.

Code

Here is how our algorithm will look; only the highlighted lines have changed from Permutation in a String:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
class Solution:
    def findSubstring(self, str1, pattern):
        window_start, matched, substr_start = 0, 0, 0
        min_length = len(str1) + 1
        char_frequency = {}

        for chr in pattern:
            if chr not in char_frequency:
                char_frequency[chr] = 0
            char_frequency[chr] += 1

        # try to extend the range [window_start, window_end]
        for window_end in range(len(str1)):
            right_char = str1[window_end]
            if right_char in char_frequency:
                char_frequency[right_char] -= 1
                if char_frequency[right_char] >= 0:  # Count every matching of a character
                    matched += 1

            # Shrink the window if we can, finish as soon as we remove a matched character
            while matched == len(pattern):
                if min_length > window_end - window_start + 1:
                    min_length = window_end - window_start + 1
                    substr_start = window_start

                left_char = str1[window_start]
                window_start += 1
                if left_char in char_frequency:
                    # Note that we could have redundant matching characters, therefore we'll
                    # decrement the matched count only when a useful occurrence of a matched
                    # character is going out of the window
                    if char_frequency[left_char] == 0:
                        matched -= 1
                    char_frequency[left_char] += 1

        if min_length > len(str1):
            return ""
        return str1[substr_start:substr_start + min_length]


def main():
    sol = Solution()
    print(sol.findSubstring("aabdec", "abc"))
    print(sol.findSubstring("aabdec", "abac"))
    print(sol.findSubstring("abdbca", "abc"))
    print(sol.findSubstring("adcad", "abc"))


main()

Time Complexity

The time complexity of the above algorithm will be O(N + M) where ‘N’ and ‘M’ are the number of characters in the input string and the pattern respectively.

Space Complexity

The space complexity of the algorithm is O(M) since in the worst case, the whole pattern can have distinct characters which will go into the HashMap. In the worst case, we also need O(N) space for the resulting substring, which will happen when the input string is a permutation of the pattern.

*Problem Challenge 4

Top Interview 150 | 30. Substring with Concatenation of All Words Design Gurus Educative.io

Words Concatenation (hard)

Given a string and a list of words, find all the starting indices of substrings in the given string that are a concatenation of all the given words exactly once without any overlapping of words. It is given that all words are of the same length.

Example 1:

1
2
3
Input: String="catfoxcat", Words=["cat", "fox"]
Output: [0, 3]
Explanation: The two substring containing both the words are "catfox" & "foxcat".

Example 2:

1
2
3
Input: String="catcatfoxfox", Words=["cat", "fox"]
Output: [3]
Explanation: The only substring containing both the words is "catfox".

Constraints:

  • 1 <= words.length <= 10^4
  • 1 <= words[i].length <= 30
  • words[i] consists of only lowercase English letters.
  • All the strings of words are unique.
  • 1 <= sum(words[i].length) <= 10^5

Solution

This problem follows the Sliding Window pattern and has a lot of similarities with Maximum Sum Subarray of Size K. We will keep track of all the words in a HashMap and try to match them in the given string. Here are the set of steps for our algorithm:

  1. Keep the frequency of every word in a HashMap.
  2. Starting from every index in the string, try to match all the words.
  3. In each iteration, keep track of all the words that we have already seen in another HashMap.
  4. If a word is not found or has a higher frequency than required, we can move on to the next character in the string.
  5. Store the index if we have found all the words.

Code

Here is what our algorithm will look like:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
class Solution:
    def findWordConcatenation(self, str1, words):
        if len(words) == 0 or len(words[0]) == 0:
            return []

        word_frequency = {}

        for word in words:
            if word not in word_frequency:
                word_frequency[word] = 0
            word_frequency[word] += 1

        result_indices = []
        words_count = len(words)
        word_length = len(words[0])

        for i in range((len(str1) - words_count * word_length)+1):
            words_seen = {}
            for j in range(0, words_count):
                next_word_index = i + j * word_length
                # Get the next word from the string
                word = str1[next_word_index: next_word_index + word_length]
                if word not in word_frequency:  # Break if we don't need this word
                    break

                # Add the word to the 'words_seen' map
                if word not in words_seen:
                    words_seen[word] = 0
                words_seen[word] += 1

                # No need to process further if the word has higher frequency than required
                if words_seen[word] > word_frequency.get(word, 0):
                    break

                if j + 1 == words_count:  # Store index if we have found all the words
                    result_indices.append(i)

        return result_indices


def main():
    sol = Solution()
    print(sol.findWordConcatenation("catfoxcat", ["cat", "fox"]))
    print(sol.findWordConcatenation("catcatfoxfox", ["cat", "fox"]))


main()

Time Complexity

The time complexity of the above algorithm will be O(N M Len) where ‘N’ is the number of characters in the given string, ‘M’ is the total number of words, and ‘Len’ is the length of a word.

Space Complexity

The space complexity of the algorithm is O(M) since at most, we will be storing all the words in the two HashMaps. In the worst case, we also need O(N) space for the resulting list. So, the overall space complexity of the algorithm will be O(M+N).

Author：Hasuer

Link：https://hasuer.github.io/3-pattern-sliding-window/index.html

Publish date：May 3rd 2024, 11:11:31 am

Update date：May 28th 2024, 11:27:28 am

License：本文采用知识共享署名-非商业性使用 4.0 国际许可协议进行许可

CATALOG
  1. 1. Introduction
  2. 2. Maximum Sum Subarray of Size K (easy)
    1. 2.1. Problem Statement
    2. 2.2. Solution
    3. 2.3. Code
      1. 2.3.1. Time Complexity
      2. 2.3.2. Space Complexity
  3. 3. Smallest Subarray with a given sum (easy)
    1. 3.1. Problem Statement
    2. 3.2. Solution
    3. 3.3. Code
      1. 3.3.1. Time Complexity
      2. 3.3.2. Space Complexity
  4. 4. Longest Substring with K Distinct Characters (medium)
    1. 4.1. Problem Statement
    2. 4.2. Solution
    3. 4.3. Code
      1. 4.3.1. Time Complexity
      2. 4.3.2. Space Complexity
  5. 5. Fruits into Baskets (medium)
    1. 5.1. Solution
    2. 5.2. Code
      1. 5.2.1. Time Complexity
      2. 5.2.2. Space Complexity
    3. 5.3. Similar Problems
  6. 6. No-repeat Substring (hard)
    1. 6.1. Problem Statement
    2. 6.2. Solution
    3. 6.3. Code
      1. 6.3.1. Time Complexity
      2. 6.3.2. Space Complexity
  7. 7. *Longest Substring with Same Letters after Replacement (hard)
    1. 7.1. Problem Statement
    2. 7.2. Solution
    3. 7.3. Code
      1. 7.3.1. Time Complexity
      2. 7.3.2. Space Complexity
  8. 8. Longest Subarray with Ones after Replacement (hard)
    1. 8.1. Problem Statement
    2. 8.2. Solution
    3. 8.3. Code
      1. 8.3.1. Time Complexity
      2. 8.3.2. Space Complexity
  9. 9. *Problem Challenge 1
    1. 9.1. Permutation in a String (hard)
    2. 9.2. Solution
    3. 9.3. Code
      1. 9.3.1. Time Complexity
      2. 9.3.2. Space Complexity
  10. 10. Problem Challenge 2
    1. 10.1. String Anagrams (hard)
    2. 10.2. Solution
    3. 10.3. Code
      1. 10.3.1. Time Complexity
      2. 10.3.2. Space Complexity
  11. 11. Problem Challenge 3
    1. 11.1. Smallest Window containing Substring (hard)
    2. 11.2. Solution
    3. 11.3. Code
      1. 11.3.1. Time Complexity
      2. 11.3.2. Space Complexity
  12. 12. *Problem Challenge 4
    1. 12.1. Words Concatenation (hard)
    2. 12.2. Solution
    3. 12.3. Code
      1. 12.3.1. Time Complexity
      2. 12.3.2. Space Complexity
Total : 41
2024
2022
2021
Interview
技术笔记 Grokking-Interview-Pattern