

Hasuer's Studio.

Hasuer's Studio.

20. Pattern Greedy Algorithms



20. Pattern Greedy Algorithms

Grokking Interview Pattern Interview

Word count: 7kReading time: 42 min

 2024/05/20   Share

• 
• 
• 
• 
• 

Introduction to Greedy Algorithm

Understanding Greedy Algorithm

A Greedy algorithm is used to solve problems in which the best choice is made at each step, and it finds a solution in a minimal step. This approach assumes that choosing a local optimum at each stage will lead to the determination of a global optimum. It’s like making the most beneficial decision at every crossroad, hoping it leads to the ultimate destination efficiently.

Purpose of Greedy Algorithm

The main goal of a greedy algorithm is to solve complex problems by breaking them down into simpler subproblems, solving each one optimally to find a solution that is as close as possible to the overall optimum. It’s particularly useful in scenarios where the problem exhibits the properties of greedy choice and optimal substructure.

Properties for Greedy Algorithm Suitability

1. Greedy Choice Property: The local optimal choices lead to a global optimum, meaning the best solution in each small step leads to the best overall solution.
2. Optimal Substructure: A problem has an optimal substructure if an optimal solution to the entire problem contains the optimal solutions to its subproblems.

Characteristics of Greedy Method

1. Local Optimization: At every step, the algorithm makes a choice that seems the best at that moment, aiming for local optimality.
2. Irrevocability: Once a choice is made, it cannot be undone or revisited. This is a key characteristic that differentiates greedy methods from dynamic programming, where decisions can be re-evaluated.

Components of Greedy Algorithm

1. Candidate Set: The set of choices available at each step.
2. Selection Function: This function helps in choosing the most promising candidate to be added to the current solution.
3. Feasibility Function: It checks if a candidate can be used to contribute to a solution without violating problem constraints.
4. Objective Function: This evaluates the value or quality of the solution at each step.
5. Solution Function: It determines if a complete solution has been reached.

Simplified Greedy Algorithm Process

1. Start with an Empty Solution Set: The algorithm begins with no items in the solution set.
2. Iterative Item Selection: In each step, choose the most suitable item based on the current goal.
3. Add Item to Solution Set: The selected item is added to the solution set.
4. Feasibility Check: Determine if the solution set with the new item still meets the problem’s constraints.
5. Accept or Reject the Item:
   • If Feasible: Keep the item in the solution set.
   • If Not Feasible: Remove and permanently discard the item.
6. Repeat Until Complete: Continue this process until a full solution is formed or no feasible solution can be found.
7. Assess Final Solution: Evaluate the completed solution set against the problem’s objectives.

Let’s understand the greedy algorithm via the example below.

Problem Statement (Boats to Save People)

881. Boats to Save People Design Gurus

We are given an array people where each element people[i] represents the weight of the i-th person. There is also a weight limit for each boat. Each boat can carry at most two people at a time, but the combined weight of these two people must not exceed limit. The objective is to determine the minimum number of boats required to carry all the people.

Example

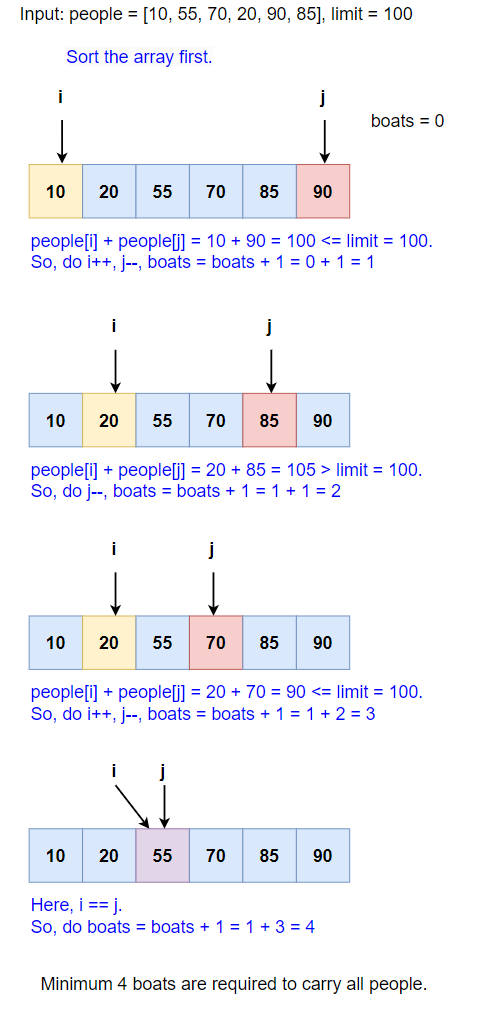
Input: people = [10, 55, 70, 20, 90, 85], limit = 100
Output: 4
Explanation: One way to transport all people using 4 boats is as follows:

• Boat 1: Carry people with weights 10 and 90 (total weight = 100).
• Boat 2: Carry a person with weight 85 (total weight = 85).
• Boat 3: Carry people with weights 20 and 70 (total weight = 90).
• Boat 4: Carry people with weights 55 (total weight = 55).

Algorithm

1. Sort the Array: Sort the people array in ascending order.

Arrays.sort(people);

1. Initialize Two Pointers: Set two pointers, i at the start (lightest person) and j at the end (heaviest person) of the array.

2. Select Optimal Pairs: Iterate through the array and pair the lightest person with the heaviest person if their combined weight is within the limit.

if (people[i] + people[j] <= limit) {
    i++; // Move to the next lightest person
}

1. Count Boats: For each iteration, increment the boat count. Move the j pointer to the left (next heaviest person).

2. Repeat Until All Are Accounted For: Continue until all people are accounted for (i.e., until i < j).

3. If i == j, increment the boat count by 1 to arrange boat for last remaining person.

4. Return the Boat Count: The total count of boats is the minimum number required.

Algorithm Walkthrough

Code

class Solution:
    def numRescueBoats(self, people, limit):
        people.sort() # Sort the list in ascending order
        i = 0 # Pointer for the lightest person
        j = len(people) - 1 # Pointer for the heaviest person
        boats = 0 # Count of boats

        while i < j:
            if people[i] + people[j] <= limit:
                # If the lightest and heaviest person can share a boat
                i += 1 # Move to the next lightest person
            j -= 1 # Move to the next heaviest person
            boats += 1 # Increment boat count

            # When last person is left.
            if i == j:
                boats += 1
        return boats # Return the total number of boats needed

solution = Solution()
people = [10, 55, 70, 20, 90, 85]
limit = 100

result = solution.numRescueBoats(people, limit)
print("Minimum number of boats required:", result)
# Expected output: "Minimum number of boats required: 2"

In the above problem, the greedy approach is applied through the strategy of pairing the lightest and heaviest individuals to optimize boat usage. After sorting the people by weight, the algorithm iteratively pairs the lightest person (at the start of the array) with the heaviest (at the end), maximizing the use of each boat’s capacity. This method ensures that each boat carries as much weight as possible without exceeding the limit, effectively reducing the total number of boats needed.

The essence of the greedy method here is making the most efficient pairing choice at each step, aiming for an overall optimal solution - the minimum number of boats to transport everyone.

Pros of Greedy Approach

• Efficiency in Time and Space: Greedy algorithms often have lower time and space complexities, making them fast and memory-efficient.
• Ease of Implementation: They are generally simpler and more straightforward to code than other complex algorithms.
• Optimal for Certain Problems: In problems with certain structures, like those with greedy-choice property and optimal substructure, greedy algorithms guarantee an optimal solution.
• Useful for Approximations: When an exact solution is not feasible, greedy algorithms can provide a close approximation quickly.

Cons of Greedy Approach with Example

• Not Always Optimal: Greedy algorithms do not always yield the global optimum solution, especially in problems lacking a greedy-choice property.
• Shortsighted Approach: They make decisions based only on current information, without considering the overall problem.
• Example: Consider the below tree where each path has a certain weight, and we need to find the path with the highest weight.

      2
    /   \
   1     3
  / \     \
20   8     7

In the given tree, a greedy approach, which selects the path with the highest immediate weight at each step, would choose the path 2 → 3 → 7, resulting in a total weight of 12.

However, this is not the optimal path. The path 2 → 1 → 20, although starting with a lower weight at the first decision point, leads to a higher total weight of 23. This example demonstrates how the greedy approach can fail to find the best solution, as it overlooks the long-term benefits of initially less attractive choices.

Standard Greedy Algorithms

• Kruskal’s Minimum Spanning Tree Algorithm: Builds a minimum spanning tree by adding the shortest edge that doesn’t form a cycle.
• Prim’s Minimum Spanning Tree Algorithm: Grows a minimum spanning tree from a starting vertex by adding the nearest vertex.
• Dijkstra’s Shortest Path Algorithm: Finds the shortest path from a single source to all other vertices in a weighted graph.
• Huffman Coding: Used for data compression, it builds a binary tree with minimum weighted path lengths for given characters.
• Fractional Knapsack Problem: Maximizes the total value of items in a knapsack without exceeding its capacity.
• Activity Selection Problem: Select the maximum number of activities that don’t overlap in time.
• Greedy Best-First Search: Used in AI for pathfinding and graph traversal, prioritizing paths that seem closest to the goal.

Let’s start solving the problem which are based on the greedy algorithm.

Valid Palindrome II

680. Valid Palindrome II Design Gurus

Problem Statement

Given string s, determine whether it’s possible to make a given string palindrome by removing at most one character.

A palindrome is a word or phrase that reads the same backward as forward.

Examples

1. Example 1:
   • Input: "racecar"
   • Expected Output: true
   • Justification: The string is already a palindrome, so no removals are needed.
2. Example 2:
   • Input: "abeccdeba"
   • Expected Output: true
   • Justification: Removing the character ‘d’ forms the palindrome “abccba”.
3. Example 3:
   • Input: "abcdef"
   • Expected Output: false
   • Justification: No single character removal will make this string a palindrome.

Constraints:

• 1 <= s.length <= 10^5
• str consists of lowercase English letters.

Solution

To solve this problem, we use a two-pointer approach that initiates at both ends of the string. These pointers move towards the center, comparing characters at each step. Upon encountering a mismatch, the algorithm decides whether to skip the character at the left or the right pointer. A helper function is used to check if the resulting substring (after skipping a character) forms a palindrome. This process is performed twice, once for each pointer. If either scenario results in a palindrome, the original string can be considered a valid palindrome after removing at most one character. This efficient method determines the feasibility of forming a palindrome with minimal alterations to the string.

1. Initialization: Begin by initializing the left pointer with 0 and the right pointer with n - 1, where n is a string length.
2. Two-Pointer Traversal: Use two pointers, and move these pointers towards the center, comparing the characters at each step.
3. Handling Mismatch: Upon encountering a mismatch, the algorithm checks two scenarios: removing the character at the left pointer or at the right pointer. For each scenario, it checks if the remaining substring forms a palindrome.
4. Greedy Decision Making: If either resulting substring is a palindrome, return true. This decision is based on the greedy principle that choosing the first viable option (resulting in a palindrome) is sufficient.
5. Concluding Result: If neither scenario results in a palindrome, the algorithm concludes that it’s impossible to form a palindrome by removing just one character and returns false.

This greedy approach is efficient as it minimizes the number of checks needed to determine if the string can be a valid palindrome with a single character removal.

Algorithm Walkthrough

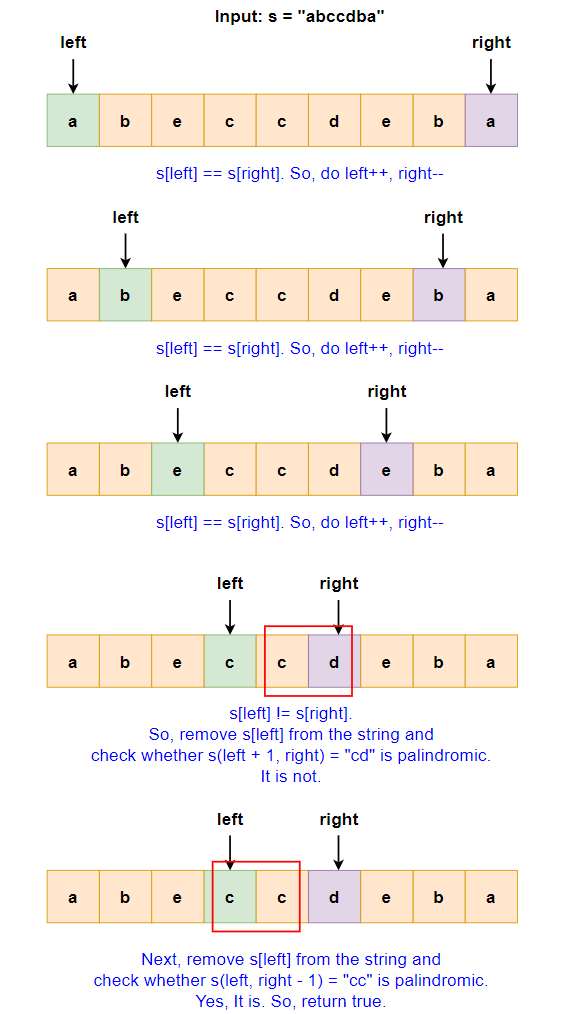
Input:- “abeccdeba”

1. Initial Setup:
   • Two pointers are initialized: left at the start (pointing to 'a') and right at the end (pointing to 'a').
2. First Iteration:
   • Compare characters at left and right pointers.
   • Characters are the same ('a'), so move left to the right and right to the left.
3. Second Iteration:
   • Now left points to 'b' and right points to 'b'.
   • Characters match, so move left and right inward again.
4. Third Iteration:
   • left is now at 'e', and right is at 'e'.
   • Characters match, so move left and right inward again.
5. Fourth Iteration:
   • left is now at 'c', and right is at 'd'.
   • Characters do not match. This is where a decision is made.
6. Checking Substrings:
   • Remove the character at the left pointer ('c') and check if the substring "cd" is a palindrome. It is not.
   • Remove the character at the right pointer ('d') and check if the substring "cc" is a palindrome. It is a palindrome.
7. Conclusion:
   • Since removing the character 'd' (at the right pointer) resulted in a palindrome, the answer is true.

Code

Here is the code for this algorithm:

class Solution:
    def isPalindromePossible(self, s: str) -> bool:
        """Check if it's possible to form a palindrome by removing at most one character"""
        left, right = 0, len(s) - 1

        while left < right:
            if s[left] != s[right]:
                # Check if either substring (after removing one char) is a palindrome
                return self.isPalindrome(s, left + 1, right) or self.isPalindrome(s, left, right - 1)
            left += 1
            right -= 1
        return True

    def isPalindrome(self, s: str, left: int, right: int) -> bool:
        """Helper function to check if a substring is a palindrome"""
        while left < right:
            if s[left] != s[right]:
                return False
            left += 1
            right -= 1
        return True

if __name__ == "__main__":
    solution = Solution()
    print(solution.isPalindromePossible("racecar"))  # true
    print(solution.isPalindromePossible("abccdba"))  # true
    print(solution.isPalindromePossible("abcdef"))   # false

Complexity Analysis

• Time Complexity: O(n) for traversing the string.
• Space Complexity: O(1) as no extra space is used.

Maximum Length of Pair Chain

646. Maximum Length of Pair Chain Design Gurus 类似Pattern Merge Intervals. 都要先排序

Problem Statement

Given a collection of pairs where each pair contains two elements [a, b], find the maximum length of a chain you can form using pairs.

A pair [a, b] can follow another pair [c, d] in the chain if b < c.

You can select pairs in any order and don’t need to use all the given pairs.

Examples

1. Example 1:
   • Input: [[1,2], [3,4], [2,3]]
   • Expected Output: 2
   • Justification: The longest chain is [1,2] -> [3,4]. The chain [1,2] -> [2,3] is invalid because 2 is not smaller than 2.
2. Example 2:
   • Input: [[5,6], [1,2], [8,9], [2,3]]
   • Expected Output: 3
   • Justification: The chain can be [1,2] -> [5,6] -> [8,9] or [2,3] -> [5,6] -> [8, 9].
3. Example 3:
   • Input: [[7,8], [5,6], [1,2], [3,5], [4,5], [2,3]]
   • Expected Output: 3
   • Justification: The longest possible chain is formed by chaining [1,2] -> [3,5] -> [7,8].

Constraints:

• n == pairs.length
• 1 <= n <= 1000
• -1000 <= lefti < righti <= 1000

Solution

The greedy approach to solving the problem involves initially sorting the pairs based on their second elements. This step is crucial as it aligns the pairs in a way that the one with the smallest end is considered first, leading to more opportunities for chain extension.

After sorting, we iterate through the pairs, maintaining a variable to track the current end of the chain. For each pair, if the first element is greater than the current chain end, we extend the chain by adding this pair and updating the chain end to this pair’s second element. This method ensures that at each step, we’re making the most optimal choice to extend the chain without needing to consider previous pairs, thereby maximizing the number of pairs in the chain with the least end values first, leading to the longest possible chain.

1. Sorting the Pairs: Initially, sort all pairs based on their second element in ascending order. This ensures that as you iterate through the pairs, you are always considering the pair with the next smallest endpoint.
2. Initializing Variables: Start with two variables: one to keep track of the current endpoint of the chain (currentEnd) and another to count the number of pairs in the chain (chainCount). Initialize currentEnd to the lowest possible value (e.g., Integer.MIN_VALUE) and chainCount to 0.
3. Iterating and Choosing Pairs: Iterate through the sorted pairs. For each pair, check if its first element is greater than currentEnd. If it is, it means this pair can be appended to the current chain. Update currentEnd to the second element of this pair and increment chainCount.
4. Result: After iterating through all pairs, chainCount will hold the maximum number of pairs that can be chained.

This Greedy approach is effective because it always chooses the option that seems best at the moment (the pair with the smallest endpoint) and this local optimal choice leads to a globally optimal solution in this specific problem context. The logic behind this is that by choosing the pair with the smallest endpoint, you are maximizing the potential for other pairs to be chained afterward.

Algorithm Walkthrough

1. Input Pairs: [[7,8], [5,6], [1,2], [3,5], [4,5], [2,3]]
2. After Sorting by Second Element: [[1,2], [2,3], [3,5], [4,5], [5,6], [7,8]]
3. Iterating through Pairs:
   • Start with currentEnd = Integer.MIN_VALUE and chainCount = 0.
   • Pair [1,2]: 1 > Integer.MIN_VALUE. Update currentEnd to 2, chainCount to 1.
   • Pair [2,3]: 2 > 2 is false. Skip.
   • Pair [3,5]: 3 > 2. Update currentEnd to 5, chainCount to 2.
   • Pair [4,5]: 4 > 5 is false. Skip.
   • Pair [5,6]: 5 > 5 is false. Skip.
   • Pair [7,8]: 7 > 5. Update currentEnd to 8, chainCount to 3.
4. Result: chainCount = 3 indicates the maximum number of pairs that can be chained.

Code

Here is the code for this algorithm:

# 官方原版是对end进行排序，但是我认为也可以对start来排序，但是需要注意，如果按照start排序，就要从后往前遍历
class Solution:
    def findLongestChain(self, pairs):
        # Sort pairs based on their second element in ascending order
        pairs.sort(key=lambda x: x[1])

        currentEnd = float('-inf')  # Current end of the chain
        chainCount = 0  # Count of pairs in the chain

        # Iterate through the sorted pairs
        for pair in pairs:
            # Check if the first element of the pair is greater than the current end
            if pair[0] > currentEnd:
                # Update the current end and increment the chain count
                currentEnd = pair[1]
                chainCount += 1

        return chainCount  # Return the maximum chain length


# Example Test Cases
solution = Solution()
example1 = [[1, 2], [3, 4], [2, 3]]
example2 = [[5, 6], [1, 2], [8, 9], [2, 3]]
example3 = [[7, 8], [5, 6], [1, 2], [3, 5], [4, 5], [2, 3]]

print("Example 1:", solution.findLongestChain(example1))  # Expected Output: 2
print("Example 2:", solution.findLongestChain(example2))  # Expected Output: 3
print("Example 3:", solution.findLongestChain(example3))  # Expected Output: 3


# 按照start排序，从后往前遍历
class Solution:
    def findLongestChain(self, pairs):
        # Sort pairs based on their second element in ascending order
        pairs.sort(key=lambda x: x[0])

        current_start = float('inf')  # Current end of the chain
        chainCount = 0  # Count of pairs in the chain

        # Iterate through the sorted pairs
        for pair in reversed(pairs):
            # Check if the first element of the pair is greater than the current end
            if pair[1] < current_start:
                # Update the current end and increment the chain count
                current_start = pair[0]
                chainCount += 1

        return chainCount  # Return the maximum chain length


# Example Test Cases
solution = Solution()
example1 = [[1, 2], [3, 4], [2, 3]]
example2 = [[5, 6], [1, 2], [8, 9], [2, 3]]
example3 = [[7, 8], [5, 6], [1, 2], [3, 5], [4, 5], [2, 3]]

print("Example 1:", solution.findLongestChain(example1))  # Expected Output: 2
print("Example 2:", solution.findLongestChain(example2))  # Expected Output: 3
print("Example 3:", solution.findLongestChain(example3))  # Expected Output: 3

Complexity Analysis

• Time Complexity: The code takes (O(n log n)) time to run, mainly due to sorting the input pairs.
• Space Complexity: It uses (O(n)) additional space due to the input array of pairs.

Minimum Add to Make Parentheses Valid

921. Minimum Add to Make Parentheses Valid Design Gurus

Problem Statement

Given a string str containing ‘(‘ and ‘)’ characters, find the minimum number of parentheses that need to be added to a string of parentheses to make it valid.

A valid string of parentheses is one where each opening parenthesis ‘(‘ has a corresponding closing parenthesis ‘)’ and vice versa. The goal is to determine the least amount of additions needed to achieve this balance.

Examples

1. Example 1:
   • Input: “(()”
   • Expected Output: 1
   • Justification: The string has two opening parentheses and one closing parenthesis. Adding one closing parenthesis at the end will balance it.
2. Example 2:
   • Input: “))((“
   • Expected Output: 4
   • Justification: There are two closing parentheses at the beginning and two opening at the end. We need two opening parentheses before the first closing and two closing parentheses after the last opening to balance the string.
3. Example 3:
   • Input: “(()())(“
   • Expected Output: 1
   • Justification: The string has three opening parentheses and three closing parentheses, with an additional opening parenthesis at the end. Adding one closing parenthesis at the end will balance it.

Constraints:

• 1 <= s.length <= 1000
• s[i] is either ‘(‘ or ‘)’.

Solution

To solve this problem, we track the balance of parentheses as we iterate through the string. We initialize two counters: one for the balance of parentheses and another for the count of additions needed.

For each character in the string, if it’s an opening parenthesis ‘(‘, we increase the balance. If it’s a closing parenthesis ‘)’, we decrease the balance. If the balance is negative at any point (which means there are more closing parentheses than opening ones), we increment the additions counter and reset the balance to zero.

The total number of additions required is the sum of the additions counter and the absolute value of the final balance, ensuring that all unmatched opening parentheses are also accounted for. This approach efficiently computes the minimum number of parentheses to be added for the string to become valid.

1. Initialization: Start with a counter set to zero, representing the number of parentheses needed to balance the string.
2. Iterating through the String: For each character in the string, determine if it’s an opening or closing parenthesis.
3. Handling Opening Parenthesis: Increment the balance counter for each opening parenthesis, indicating a pending closing parenthesis is needed.
4. Handling Closing Parenthesis: For each closing parenthesis, if there is an unmatched opening parenthesis (balance counter > 0), decrement the balance. If not, increment the counter, indicating an additional opening parenthesis is needed.
5. Completion: The final value of the counter represents the total number of additional parentheses required to balance the string.

Algorithm Walkthrough

Let’s apply the algorithm to the input string “(()())(“:

1. Initialize Variables:
   • balance = 0
   • counter = 0
2. Iterate Through the String “(()())(“:
   • First Character ‘(‘ :
     • Increment balance → balance = 1 (1 unmatched opening parenthesis).
   • Second Character ‘(‘ :
     • Increment balance → balance = 2 (2 unmatched opening parentheses).
   • Third Character ‘)’ :
     • Decrement balance → balance = 1 (1 unmatched opening parenthesis).
   • Fourth Character ‘(‘ :
     • Increment balance → balance = 2 (2 unmatched opening parentheses).
   • Fifth Character ‘)’ :
     • Decrement balance → balance = 1 (1 unmatched opening parenthesis).
   • Sixth Character ‘)’ :
     • Decrement balance → balance = 0 (all parentheses matched so far).
   • Seventh Character ‘(‘ :
     • Increment balance → balance = 1 (1 unmatched opening parenthesis).
3. Final Calculation:
   • At the end of the string, balance = 1 and counter = 0.
   • Add counter and balance → 0 + 1 = 1.
4. Return Result:
   • The final result is 1, indicating that 1 additional closing parenthesis is required to make the string “(()())(“ valid.

This walkthrough demonstrates that to balance the given string “(()())(“, we need to add just one closing parenthesis.

Code

Here is the code for this algorithm:

# 感觉和这个背景类似，但是方法不一样哦
# https://hasuer.github.io/15-pattern-subsets/index.html#/Balanced-Parentheses-hard
class Solution:
    def minAddToMakeValid(self, S: str) -> int:
        balance, counter = 0, 0
        for char in S:
            # Increment balance for '(', decrement for ')'
            balance += 1 if char == '(' else -1
            # If balance is negative, we have more ')' than '('
            if balance == -1:
                counter += 1  # Increment counter for each unmatched ')'
                balance += 1  # Reset balance as we've accounted for the unmatched ')'
        return counter + balance  # Sum is the total adjustments needed


if __name__ == "__main__":
    solution = Solution()
    # Testing the algorithm with the three examples
    print(solution.minAddToMakeValid("(()"))  # Example 1
    print(solution.minAddToMakeValid("))(("))  # Example 2
    print(solution.minAddToMakeValid("(()())("))  # Example 3

Complexity Analysis

• Time Complexity: The time complexity of this algorithm is O(n), where n is the length of the string. This is because we iterate through the string once.
• Space Complexity: The space complexity is O(1), as we only use a fixed amount of additional space (counter and balance variables) regardless of the input size.

*Remove Duplicate Letters

316. Remove Duplicate Letters Design Gurus

Problem Statement

Given a string s, remove all duplicate letters from the input string while maintaining the original order of the letters.

Additionally, the returned string should be the smallest in lexicographical order among all possible results.

Examples:

1. • Input: “bbaac”
   • Expected Output: “bac”
   • Justification: Removing the extra ‘b’ and one ‘a’ from the original string gives ‘bac’, which is the smallest lexicographical string without duplicate letters.
2. • Input: “zabccde”
   • Expected Output: “zabcde”
   • Justification: Removing one of the ‘c’s forms ‘zabcde’, the smallest string in lexicographical order without duplicates.
3. • Input: “mnopmn”
   • Expected Output: “mnop”
   • Justification: Removing the second ‘m’ and ‘n’ gives ‘mnop’, which is the smallest possible string without duplicate characters.

Constraints:

• 1 <= s.length <= 10^4
• s consists of lowercase English letters.

Solution

To solve the given problem, begin by iterating through the string, and calculate the frequency count for each character. We will use the stack to maintain the order of characters and the set to track the uniqueness of characters.

Next, start traversing the string, and for every character encountered, check if it’s already in the ‘present’ set. If it’s not, compare it with the top element of the ‘result’ stack. If the stack is not empty, and the current character is lexicographically smaller than the stack’s top, and the top character of the stack appears again in the string (indicated by a non-zero frequency count), repeatedly pop the stack and remove those elements from the ‘present’ set. Then, add the current character to the stack and the ‘present’ set.

This process, facilitated by the stack and set, ensures that the stack is built with unique characters in the smallest lexicographical order. After processing the entire string, pop elements from the stack to construct the final string, thereby obtaining the smallest lexicographical sequence without duplicate characters.

1. Frequency Count (count):

   • Initialize a count dictionary (or hash map in some languages) to store the frequency of each character in the string s.

2. Character Presence Tracking (present):

   • Use a set present to keep track of the characters that have been added to the resultant string. This set prevents duplicate characters in the result.

3. Building the Result (result):

   • Create a stack result to construct the final string.

   • For each character c in the string s:

     • If c is not in present, proceed to compare it with the top character of result.
     • While result is not empty, and c is lexicographically smaller than the top character of result, and the frequency of the top character of result is more than 0 (indicating it appears again in the string), pop the top character from result and remove it from present.
     • Push c onto result and add it to present.
     • Decrement the frequency of c in count.

4. Result Construction:

   • The stack result now contains the characters of the final string in reverse order. Pop elements from result to construct the output string in the correct order, from left to right.

This approach works because it ensures that the smallest character is placed first, respecting the original order and removing duplicates. The frequency count ensures that characters are not wrongly discarded.

Algorithm Walkthrough:

Input: “zabccde”

1. Initialization:
   • Calculate the frequency of each character: {'z': 1, 'a': 1, 'b': 1, 'c': 2, 'd': 1, 'e': 1}.
   • Initialize an empty stack result and a set present to keep track of characters already in result.
2. Iteration Over Characters:
   • ‘z’: Not in present. Add ‘z’ to result, add to present. Decrease frequency of ‘z’.
   • ‘a’: Not in present. As ‘a’ is smaller than ‘z’, but ‘z’ won’t appear again (frequency is now 0), we keep ‘z’. Add ‘a’ to result, add to present. Decrease frequency of ‘a’.
   • ‘b’: Not in present. Add ‘b’ to result, add to present. Decrease frequency of ‘b’.
   • First ‘c’: Not in present. Add ‘c’ to result, add to present. Decrease frequency of ‘c’.
   • Second ‘c’: Already in present. Skip it.
   • ‘d’: Not in present. Add ‘d’ to result, add to present. Decrease frequency of ‘d’.
   • ‘e’: Not in present. Add ‘e’ to result, add to present. Decrease frequency of ‘e’.
3. Result Construction:
   • The result stack now contains ['z', 'a', 'b', 'c', 'd', 'e'].
   • Convert the stack to a string to get the final result: “zabcdef”.

Expected Output: “zabcdef”

Code

Here is the code for this algorithm:

# 本来感觉官方的写法好复杂，但是自己用了min_heap、OrderedDict试了一下是错的
from collections import deque


class Solution:
    def removeDuplicateLetters(self, s: str) -> str:
        # Count the frequency of each character
        count = {char: s.count(char) for char in set(s)} # 这里的顺序是不确定的
        stack = deque()  # Stack for the result string
        present = set()  # Set to track if a character is in the result

        for char in s:
            # Only add character if it's not already in the result
            if char not in present:
                # Ensure the smallest lexicographical order
                while stack and char < stack[-1] and count[stack[-1]] > 0:
                    present.remove(stack.pop())
                stack.append(char)
                present.add(char)
            count[char] -= 1  # Decrease the frequency

        return ''.join(stack)


# Test cases
sol = Solution()
print(sol.removeDuplicateLetters("bbaac"))  # Output: "bac"
print(sol.removeDuplicateLetters("zabccde"))  # Output: "zabcde"
print(sol.removeDuplicateLetters("mnopmn"))  # Output: "mnop"

Complexity Analysis:

• Time Complexity: O(N) where N is the length of the string. Each character is visited once.
• Space Complexity: O(1) as the extra space used does not depend on the input size. The character count and the stack size are bounded by the character set size (constant).

Largest Palindromic Number

2384. Largest Palindromic Number Design Gurus

类似 Pattern Hash Maps 中的Longest Palindrome(easy)

Problem Statement

Given a string s containing 0 to 9 digits, create the largest possible palindromic number using the string characters.

A palindromic number reads the same backward as forward.

If it’s not possible to form such a number using all digits of the given string, you can skip some of them.

Examples

1. • Input: “323211444”
   • Expected Output: “432141234”
   • Justification: This is the largest palindromic number that can be formed from the given digits.
2. • Input: “998877”
   • Expected Output: “987789”
   • Justification: “987789” is the largest palindrome that can be formed.
3. • Input: “54321”
   • Expected Output: “5”
   • Justification: Only “5” can form a valid palindromic number as other digits cannot be paired.

Constraints:

• 1 <= num.length <= 105
• num consists of digits.

Solution

To solve this problem, begin by counting the frequency of each character in the provided string.

Next, construct the palindrome in two halves. Start with the first half: for each digit, use half of its total occurrences and add digits in descending order. If a digit occurs an odd number of times, set aside one occurrence for the middle of the palindrome. The middle element should be the largest digit that appears an odd number of times. Once the first half is complete, replicate it in reverse order to form the second half.

In cases where there’s no first half but there is a single digit with an odd count, use that digit as the palindrome. If it’s not possible to form any palindrome, return “0”.

1. Count Digit Frequencies: Determine how many times each digit appears in the input.
2. Construct the First Half: Arrange the digits in descending order for the first half, ensuring to use each digit an even number of times.
3. Middle Digit Consideration: Reserve one instance of the largest digit that occurs an odd number of times for the middle of the palindrome.
4. Complete the Palindrome: Mirror the first half to form the second half of the palindrome.

This approach is efficient because it maximizes the value of the palindrome by using the largest digits in the most significant positions.

Algorithm Walkthrough

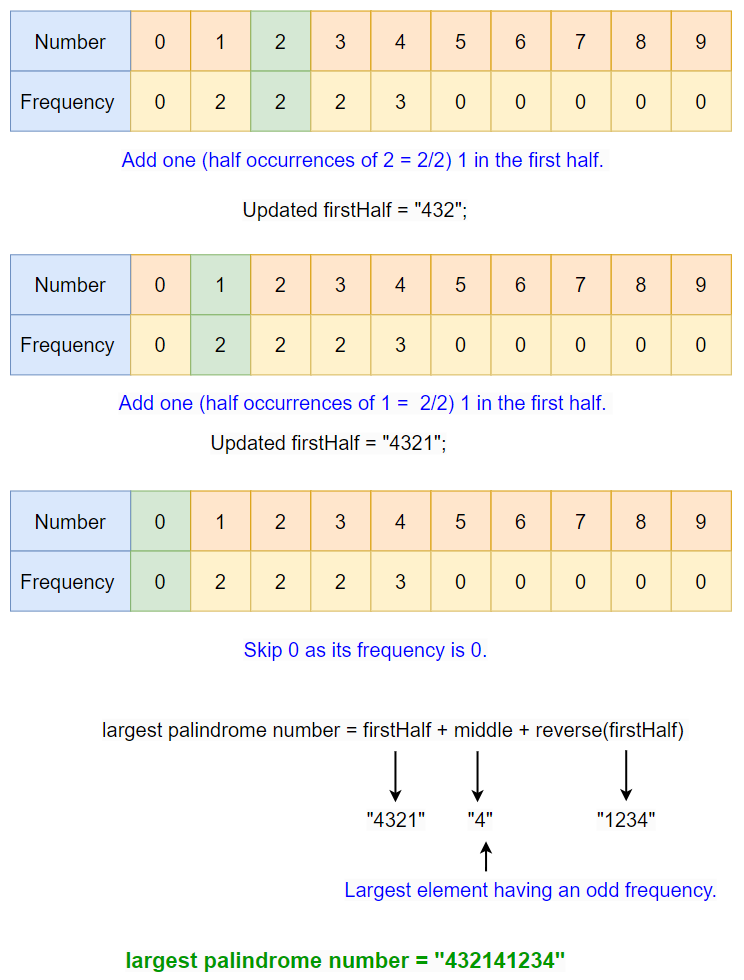
Input “323211444”

1. Count Digit Frequencies:
   • Iterate over each digit in the string “323211444”.
   • Count the occurrences of each digit. For example, the digit ‘1’ appears twice, ‘2’ appears twice, ‘3’ once, and ‘4’ thrice.
2. Build the First Half of the Palindrome:
   • Start from the largest digit (9) and move down to the smallest (0).
   • Skip digits that do not appear in the count.
   • For each digit that does appear, add half of its occurrences to the first half of the palindrome. For instance, add one ‘4’s, one ‘3’, one ‘2’, and one ‘1’.
   • Reserve one occurrence of the digit with the highest value that appears an odd number of times for the middle of the palindrome if necessary. In this case, ‘4’ appears three times, so one ‘4’ is reserved.
3. Determine the Middle Digit:
   • Identify the largest digit that has an odd frequency. In “312211444”, it’s ‘4’.
   • This will be the middle digit of the palindrome.
4. Complete the Palindrome:
   • Mirror the first half of the palindrome to create the second half.
   • Combine the first half, the middle digit (if any), and the mirrored second half to form the final palindromic number.
   • In this case, the first half is “4321”, the middle digit is ‘4’, and the mirrored second half is “1234”, making the complete palindrome “432141234”.

Code

Here is the code for this algorithm:

# 但是这个有点问题，在这一部分上“Handle special cases”，如果是"00001"应该返回的是1，但是现在返回的是0
class Solution:
    def largestPalindromic(self, num: str) -> str:
        # Count the frequency of each digit in the input number
        freq = [0] * 10  # Initialize a frequency array for digits 0-9
        for digit in num:
            freq[int(digit)] += 1  # Increment the count for each digit

        first_half, middle = [], ''
        for i in range(9, -1, -1):  # Iterate from the highest digit (9) to the lowest (0)
            if freq[i] % 2 != 0 and middle == '':  # Check if the digit count is odd and middle is empty
                middle = str(i)  # Assign the largest odd-count digit as the middle digit
            first_half.extend([str(i)] * (freq[i] // 2))  # Add half of the even-count digits to the first half
            # first_half.append(str(i) * (freq[i] // 2))  # 这个也可以，这是添加元素，上面的是添加数组

        # Handle special cases
        if not first_half:
            return middle if middle else '0'  # Return the middle digit or "0"
        elif all(d == '0' for d in first_half):
            return '0'  # Case for multiple zeros
        # Construct the final palindrome
        return ''.join(first_half) + middle + ''.join(
            reversed(first_half))  # Concatenate the first half, middle digit, and the reversed first half


# Test Cases
solution = Solution()
print(solution.largestPalindromic("323211444"))  # 432141234
print(solution.largestPalindromic("998877"))  # 987789
print(solution.largestPalindromic("54321"))  # 5

# 修改之后的版本，这才可以过leetcode,上面那个不能过leetcode
class Solution:
    def largestPalindromic(self, num: str) -> str:
        # Count the frequency of each digit in the input number
        freq = [0] * 10  # Initialize a frequency array for digits 0-9
        for digit in num:
            freq[int(digit)] += 1  # Increment the count for each digit

        first_half, middle = [], ''
        for i in range(9, -1, -1):  # Iterate from the highest digit (9) to the lowest (0)
            if freq[i] % 2 != 0 and middle == '':  # Check if the digit count is odd and middle is empty
                middle = str(i)  # Assign the largest odd-count digit as the middle digit
            first_half.extend([str(i)] * (freq[i] // 2))  # Add half of the even-count digits to the first half
            # first_half.append(str(i) * (freq[i] // 2))  # 这个也可以，这是添加元素，上面的是添加数组

        # Handle special cases
        if not first_half:
            return middle if middle else '0'  # Return the middle digit or "0"
        elif all(d == '0' for d in first_half) and middle == "":
            return '0'  # Case for multiple zeros
        elif all(d == '0' for d in first_half):
            first_half = "" # 这是first-half都是0，但是middle存在的情况
        # Construct the final palindrome
        return ''.join(first_half) + middle + ''.join(
            reversed(first_half))  # Concatenate the first half, middle digit, and the reversed first half


# Test Cases
solution = Solution()
print(solution.largestPalindromic("323211444"))  # 432141234
print(solution.largestPalindromic("998877"))  # 987789
print(solution.largestPalindromic("54321"))  # 5
print(solution.largestPalindromic("00001"))  # 5

Complexity Analysis

• Time Complexity: O(n), where n is the length of the input string. The algorithm involves iterating over the input string once for frequency counting and then iterating over the frequency array (constant size of 10).
• Space Complexity: O(1), as the frequency array size is constant and does not depend on the input size.

Removing Minimum and Maximum From Array

Removing Minimum and Maximum From Array Design Gurus

Problem Statement

Determine the minimum number of deletions required to remove the smallest and the largest elements from an array of integers.

In each deletion, you are allowed to remove either the first (leftmost) or the last (rightmost) element of the array.

Examples

1. Example 1:
   • Input: [3, 2, 5, 1, 4]
   • Expected Output: 3
   • Justification: The smallest element is 1 and the largest is 5. Removing 4, 1, and then 5 (or 5, 4, and then 1) in three moves is the most efficient strategy.
2. Example 2:
   • Input: [7, 5, 6, 8, 1]
   • Expected Output: 2
   • Justification: Here, 1 is the smallest, and 8 is the largest. Removing 1 and then 8 in two moves is the optimal strategy.
3. Example 3:
   • Input: [2, 4, 10, 1, 3, 5]
   • Expected Output: 4
   • Justification: The smallest is 1 and the largest is 10. One strategy is to remove 2, 4, 10, and then 1 in four moves.

Constraints:

• 1 <= nums.length <= 105
• -105 <= nums[i] <= 105
• The integers in nums are distinct.

Solution

To solve this problem, identify the positions of the minimum and maximum elements in the array. Then, calculate the distance of these elements from both ends of the array. The key is to find the shortest path to remove both elements, considering three scenarios: removing both from the start, both from the end, one from the start and the other from the end. The minimum number of steps among these scenarios is the answer.

The steps are:

1. Find Indices of Minimum and Maximum Elements:
   • Iterate through the array to find the indices of the minimum and maximum elements. This step is essential because these positions dictate the strategy for removal.
2. Calculate Distances:
   • Calculate the distances of the minimum and maximum elements from both ends of the array.
3. Evaluate Removal Strategies:
   • There are several strategies to consider, and the goal is to find the one that requires the fewest moves:
     • Removing the minimum and maximum elements starting from the same end of the array.
     • Removing one of them from the start and the other from the end.
   • To find the optimal strategy, compare the total number of moves for each approach. This comparison involves summing up the relevant distances and determining the minimum sum.
4. Return the Minimum Number of Moves:
   • The final step is to return the smallest number of moves required among all evaluated strategies.

Algorithm Walkthrough

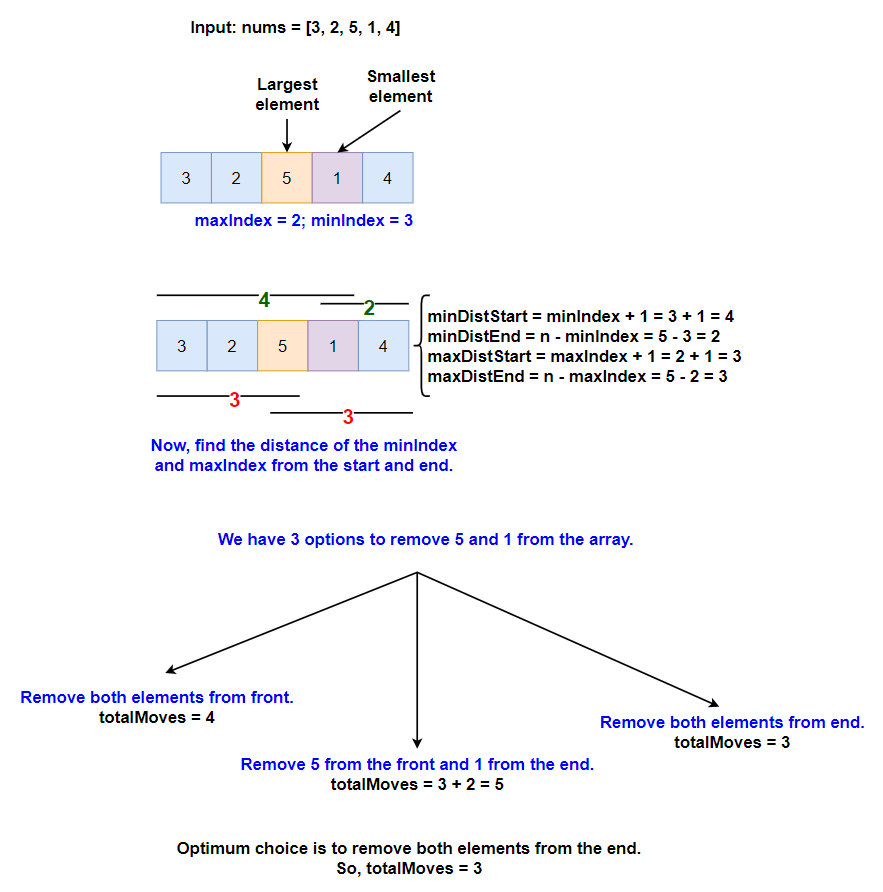
For the input [3, 2, 5, 1, 4]:

1. Identify the Smallest and Largest Elements:
   • Smallest element: 1 at index 3.
   • Largest element: 5 at index 2.
2. Calculate Distances from Both Ends:
   • Distance of 1 from the start: 4.
   • Distance of 1 from the end: 2.
   • Distance of 5 from the start: 3.
   • Distance of 5 from the end: 3.
3. Determine the Most Efficient Removal Sequence:
   • Option 1: Remove elements from start to reach 5 and then from the end to reach 1. Total moves = 3 (for 5) + 2 (for 1) = 5.
   • Option 2: Remove both elements from the end. Total moves to reach at 5 from the end is equal to 3.
   • Option 3: Remove both elements from the start. Total moves to reach at 1 from the end is equal to 4.
4. Choose the Optimal Sequence:
   • Option 2 provides the optimal result. The total number of moves required is 3.

Code

Here is the code for this algorithm:

class Solution:
    def minMoves(self, nums):
        n = len(nums)
        # Find the indexes of the minimum and maximum elements
        minIndex = nums.index(min(nums))
        maxIndex = nums.index(max(nums))

        # Calculate distances from both ends
        minDistStart = minIndex + 1
        minDistEnd = n - minIndex
        maxDistStart = maxIndex + 1
        maxDistEnd = n - maxIndex

        # Determine the most efficient sequence of moves
        totalMoves = min(
            max(minDistStart, maxDistStart),  # Both from start
            min(minDistStart + maxDistEnd, minDistEnd + maxDistStart),  # One from each end
            max(minDistEnd, maxDistEnd)  # Both from end
        )

        return totalMoves


# Testing the algorithm with example inputs
sol = Solution()
print(sol.minMoves([3, 2, 5, 1, 4]))  # Output: 3
print(sol.minMoves([7, 5, 6, 8, 1]))  # Output: 2
print(sol.minMoves([2, 4, 10, 1, 3, 5]))  # Output: 4

Complexity Analysis

• Time Complexity: The algorithm primarily involves finding the minimum and maximum elements and calculating their distances from both ends. This is a linear operation, resulting in a time complexity of O(n), where n is the length of the array.
• Space Complexity: Since no additional data structures are used that grow with the input size, the space complexity is O(1).

Author：Hasuer

Link：https://hasuer.github.io/20-pattern-greedy-algorithms/index.html

Publish date：May 20th 2024, 9:58:48 am

Update date：May 28th 2024, 11:30:07 am

License：本文采用知识共享署名-非商业性使用 4.0 国际许可协议进行许可

• Next Post
  21. Pattern 01 Knapsack (Dynamic Programming)
• Previous Post
  19. Pattern K-way merge

Powered by Hexotheme Archer

PV: :)

CATALOG

1. 1. Introduction to Greedy Algorithm
   1. 1.1. Understanding Greedy Algorithm
      1. 1.1.1. Purpose of Greedy Algorithm
      2. 1.1.2. Properties for Greedy Algorithm Suitability
      3. 1.1.3. Characteristics of Greedy Method
      4. 1.1.4. Components of Greedy Algorithm
   2. 1.2. Simplified Greedy Algorithm Process
      1. 1.2.1. Problem Statement (Boats to Save People)
      2. 1.2.2. Example
      3. 1.2.3. Algorithm
         1. 1.2.3.1. Algorithm Walkthrough
      4. 1.2.4. Code
   3. 1.3. Pros of Greedy Approach
   4. 1.4. Cons of Greedy Approach with Example
   5. 1.5. Standard Greedy Algorithms
2. 2. Valid Palindrome II
   1. 2.1. Problem Statement
      1. 2.1.1. Examples
   2. 2.2. Solution
      1. 2.2.1. Algorithm Walkthrough
   3. 2.3. Code
   4. 2.4. Complexity Analysis
3. 3. Maximum Length of Pair Chain
   1. 3.1. Problem Statement
      1. 3.1.1. Examples
   2. 3.2. Solution
      1. 3.2.1. Algorithm Walkthrough
   3. 3.3. Code
   4. 3.4. Complexity Analysis
4. 4. Minimum Add to Make Parentheses Valid
   1. 4.1. Problem Statement
      1. 4.1.1. Examples
   2. 4.2. Solution
      1. 4.2.1. Algorithm Walkthrough
   3. 4.3. Code
   4. 4.4. Complexity Analysis
5. 5. *Remove Duplicate Letters
   1. 5.1. Problem Statement
   2. 5.2. Solution
   3. 5.3. Code
   4. 5.4. Complexity Analysis:
6. 6. Largest Palindromic Number
   1. 6.1. Problem Statement
      1. 6.1.1. Examples
   2. 6.2. Solution
      1. 6.2.1. Algorithm Walkthrough
   3. 6.3. Code
   4. 6.4. Complexity Analysis
7. 7. Removing Minimum and Maximum From Array
   1. 7.1. Problem Statement
      1. 7.1.1. Examples
   2. 7.2. Solution
      1. 7.2.1. Algorithm Walkthrough
   3. 7.3. Code
   4. 7.4. Complexity Analysis

• Archive
• Tag
• Cate

Total : 41

2024

• 06/02 34. Conclusions
• 06/02 33. Test Your Knowledge (Hard)
• 06/01 32. Test Your Knowledge (Medium)
• 05/31 31. Test Your Knowledge (Easy).md
• 05/30 30. Revision
• 05/29 29. Miscellaneous
• 05/28 28. Pattern Multi-thread
• 05/27 27. Pattern Prefix Sum
• 05/26 26. Pattern Ordered Set
• 05/25 25. Pattern Union Find
• 05/24 24. Pattern Topological Sort (Graph)
• 05/23 23. Pattern Trie
• 05/22 22. Pattern Backtracking
• 05/21 21. Pattern 01 Knapsack (Dynamic Programming)
• 05/20 20. Pattern Greedy Algorithms
• 05/19 19. Pattern K-way merge
• 05/18 18. Pattern Top 'K' Elements
• 05/17 17. Pattern Bitwise XOR
• 05/16 16. Pattern Modified Binary Search
• 05/15 15. Pattern Subsets
• 05/14 14. Pattern Two Heaps
• 05/13 13. Pattern Island (Matrix traversal)
• 05/12 12. Pattern Graphs
• 05/11 11. Pattern Tree Depth First Search
• 05/10 10. Pattern Tree Breadth First Search
• 05/09 9. Pattern Hash Maps
• 05/08 8. Pattern Monotonic Stack
• 05/07 7. Pattern Stack
• 05/06 6. Pattern In-place Reversal of a LinkedList
• 05/05 5. Pattern Cyclic Sort
• 05/04 4. Pattern Merge Intervals
• 05/03 3. Pattern Sliding Window
• 05/02 2. Pattern Fast_Slow pointers
• 05/01 1. Pattern Two Pointers
• 04/30 0.Introduction

2022

• 06/12 Ubuntu20.04安装配置MySQL8(详细)
• 02/25 Axios学习笔记
• 02/23 Promise学习笔记
• 02/23 Nginx学习笔记
• 02/23 AJAX学习笔记

2021

• 07/07 Git学习笔记

 Interview



缺失模块，请参考主题文档进行安装配置：https://github.com/fi3ework/hexo-theme-archer#%E5%AE%89%E8%A3%85%E4%B8%BB%E9%A2%98

 技术笔记  Grokking-Interview-Pattern

