Hasuer's Studio.

28. Pattern Multi-thread

Grokking Interview Pattern Interview
Word count: 3.2kReading time: 19 min
2024/05/28

416. Partition Equal Subset Sum Design Gurus Educative.io

ATTENTION: 这些题目还没有看

Introduction to Multi-threaded Pattern

In many algorithms, concurrency and thread safety are very important. With technical interviews in mind, we can easily apply these concepts to most coding problems and stand out from the crowd.

Thread safety can be easily added to any algorithm that uses multiple threads.

Algorithms can be made multi-threaded to perform multiple concurrent tasks or to perform pre-fetching or post-processing functions to speed things up.

Let’s see this pattern in action.

Same Tree

Problem Statement

Given the roots of two binary trees ‘p’ and ‘q’, write a function to check if they are the same or not.

Two binary trees are considered the same if they met following two conditions:

  1. Both tree are structurally identical.
  2. Each corresponding node on both the trees have the same value.

Example 1:

Given the following two binary trees:

Output: true

Explanation: Both trees are structurally identical and have same values.

Example 2:

Given the following two binary trees:

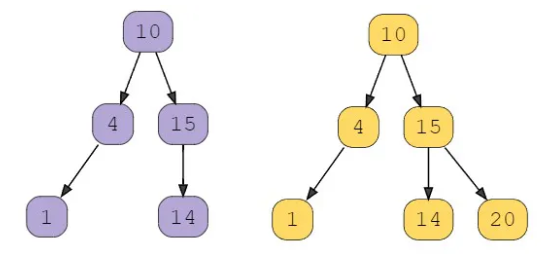
Output: false

Explanation: Trees are structurally different.

Example 3:

Given the following two binary trees:

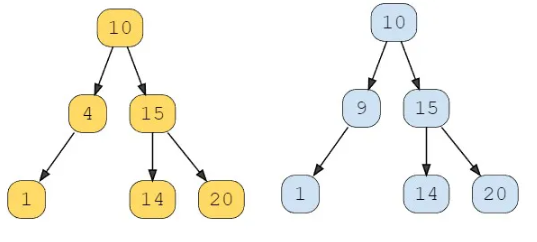
Output: false

Explanation: Corresponding nodes have different value ( 4 & 9 ).

Constraints:

  • The number of nodes in both trees is in the range [0, 100].
  • -10^4 <= Node.val <= 10^4

Solution

A simple solution would be to recursively check each corresponding node of the two trees. If one of the trees do not have a corresponding node or their values differ, we can conclude that the trees are not the same.

Code

Here is what our algorithm will look like:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
# class TreeNode:
#   def __init__(self, val):
#     self.val = val
#     self.left = None
#     self.right = None

class Solution:
  def isSameTree(self, p, q):
    # p and q are both None
    if not p and not q:
      return True
    # one of p and q is None
    if not p or not q:
      return False
    # one of p and q has a different value
    if p.val != q.val:
      return False

    # check left and right subtree recursively
    return self.isSameTree(p.right, q.right) and self.isSameTree(p.left, q.left)

if __name__ == "__main__":
  p = TreeNode(10)
  p.left = TreeNode(4)
  p.left.left = TreeNode(1)
  p.right = TreeNode(15)
  p.right.left = TreeNode(14)

  q = TreeNode(10)
  q.left = TreeNode(4)
  q.left.left = TreeNode(1)
  q.right = TreeNode(15)
  q.right.left = TreeNode(14)

  sol = Solution()
  print(sol.isSameTree(p, q))

  q.right.right = TreeNode(20)
  print(sol.isSameTree(p, q))

  p.right.right = TreeNode(20)
  print(sol.isSameTree(p, q))
  
  p.left.val = 9
  print(sol.isSameTree(p, q))

Time Complexity

The solution will take O(min(M, N)) time, where ‘M’ and ‘N’ are the number of nodes in the given trees respectively. We are taking minimum of ‘M’ and ‘N’, since as soon as we see a difference in value or structure, we do not check the remaining trees.

Space Complexity

We will need O(N) space for the recursion stack in the worst case (when the binary tree is a list). Overall, we will need to store nodes equal to the height of the tree, hence, O(H) space complexity, where H is the height of the given tree.

Making the Algorithm Multi-threaded

To further improve the algorithm, we can make isSameTree() multi-threaded to check the left and right subtrees in separate threads.

We can find how many processors the machine has on which our algorithm is running. We will, then, start multiple threads so that each core can run one thread.

We will use a Volatile Boolean variable isSame so that multiple threads can update its value concurrently.

Here is the code that takes care of this scenario:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
import os
import threading

# class TreeNode:
#     def __init__(self, val):
#         self.val = val
#         self.left = None
#         self.right = None

class Solution:
    def __init__(self):
        self.isSame = True

    def isSameTree(self, p, q):
        self.isSame = True
        num_threads = os.cpu_count()
        return self.isSameTree_multi_threaded(p, q, num_threads)

    def isSameTree_multi_threaded(self, p, q, num_threads):
        # p and q are both None
        if not p and not q:
            return True
        # one of p and q is None
        if not p or not q:
            return False
        # one of p and q has a different value
        if p.val != q.val:
            return False

        # if we can start more threads, we will spawn a new thread to check the
        # right subtree, otherwise we will do everything in the current thread
        if num_threads > 0:
            # spawn a separate thread for checking the right sub-tree
            def check_right_subtree():
                nonlocal p, q, num_threads
                self.isSame &= self.isSameTree_multi_threaded(p.right, q.right, num_threads // 2)

            t1 = threading.Thread(target=check_right_subtree)
            t1.start()

            # check the left sub-tree in the current thread
            self.isSame &= self.isSameTree_multi_threaded(p.left, q.left, num_threads // 2)

            t1.join()  # wait for the thread checking the right sub-tree
        else:  # do everything in the current thread
            self.isSame &= self.isSameTree_multi_threaded(p.right, q.right, 0) and self.isSameTree_multi_threaded(p.left, q.left, 0)

        return self.isSame


if __name__ == "__main__":
    p = TreeNode(10)
    p.left = TreeNode(4)
    p.left.left = TreeNode(1)
    p.right = TreeNode(15)
    p.right.left = TreeNode(14)

    q = TreeNode(10)
    q.left = TreeNode(4)
    q.left.left = TreeNode(1)
    q.right = TreeNode(15)
    q.right.left = TreeNode(14)

    sol = Solution()
    print(sol.isSameTree(p, q))

    q.right.right = TreeNode(20)
    print(sol.isSameTree(p, q))

    p.right.right = TreeNode(20)
    print(sol.isSameTree(p, q))

    p.left.val = 9
    print(sol.isSameTree(p, q))

Time and Space Complexities

Everything has the same complexity as the previous solution.

Invert Binary Tree

Problem Statement

Given the root of a binary tree, invert it.

Example:

Given the following two binary trees:

Constraints:

  • The number of nodes in both trees is in the range [0, 100].
  • -100 <= Node.val <= 100

Solution

This problem is quite similar to Same Tree. We can follow the same approach. After swapping left and right child of a node, we will recursively invert its left and right subtrees.

Code

Here is what our algorithm will look like:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right

class Solution:
    def invertTree(self, root):
        # Base case: if the root is None, just return None
        if root is None:
            return None
        
        # Swap the left and right children of the current node
        root.left, root.right = root.right, root.left
        
        # Recursively invert the left and right subtrees
        self.invertTree(root.left)
        self.invertTree(root.right)
        
        return root

if __name__ == "__main__":
    # Construct the binary search tree
    root = TreeNode(10)
    root.left = TreeNode(4)
    root.left.left = TreeNode(1)
    root.right = TreeNode(15)
    root.right.left = TreeNode(14)
    root.right.right = TreeNode(19)
    root.right.right.right = TreeNode(20)

    # Invert the binary search tree
    sol = Solution()
    sol.invertTree(root)
    
    # Print out the results to check if the tree was inverted correctly
    print(root.right.val == 4)  # Expect: True
    print(root.left.val == 15)  # Expect: True
    print(root.left.right.val == 14)  # Expect: True
    print(root.left.left.val == 19)  # Expect: True
    print(root.left.left.left.val == 20)  # Expect: True

Time Complexity

Since we traverse each node once, the solution will take O(N) time where ‘N’ is the total number of nodes in the tree.

Space Complexity

We will need O(N) space for the recursion stack in the worst case (when the binary tree is a list). Overall, we will need to store nodes equal to the height of the tree, hence, O(H) space complexity, where H is the height of the given tree.

Making the Algorithm Multi-threaded

To further improve the algorithm, we can make invertTree() multi-threaded to invert left and right subtrees in separate threads.

We can find how many cores the machine has on which our algorithm is running. We will, then, start multiple threads so that each core can run one thread.

Here is the code that takes care of this scenario:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
import threading
import multiprocessing

# Definition for a binary search tree node
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right

class Solution:
    
    def invertTree(self, root):
        num_threads = multiprocessing.cpu_count()  # Number of available processors
        return self.invert_tree_multithreaded(root, num_threads)

    def invert_tree_multithreaded(self, root, num_threads):
        if root is None:
            return None

        # Invert the current node
        root.left, root.right = root.right, root.left

        if num_threads > 0:
            # Spawn a separate thread to invert the left subtree
            t1 = threading.Thread(target=self.invert_tree_multithreaded, args=(root.left, num_threads // 2))
            t1.start()

            # Invert the right subtree in the same thread
            self.invert_tree_multithreaded(root.right, num_threads // 2)

            t1.join()  # Wait for the thread inverting the left subtree
        else:
            self.invert_tree_multithreaded(root.left, 0)
            self.invert_tree_multithreaded(root.right, 0)

        return root


if __name__ == '__main__':
    root = TreeNode(10)
    root.left = TreeNode(4)
    root.left.left = TreeNode(1)
    root.right = TreeNode(15)
    root.right.left = TreeNode(14)
    root.right.right = TreeNode(19)
    root.right.right.right = TreeNode(20)

    sol = Solution()
    sol.invertTree(root)

    print(root.right.val == 4)  # Expected: True
    print(root.left.val == 15)  # Expected: True
    print(root.left.right.val == 14)  # Expected: True
    print(root.left.left.val == 19)  # Expected: True
    print(root.left.left.left.val == 20)  # Expected: True

Time and Space Complexities

Everything has the same complexity as the previous solution.

Binary Search Tree Iterator

Problem Statement

Implement an iterator for the in-order traversal of a binary search tree (BST). That is, given a BST, we need to implement two functions:

bool hasNext(): Returns true if at least one element is left in the in-order traversal of the BST. int next(): Return the next element in the in-order traversal of the BST.

Example:

Given the following BST:

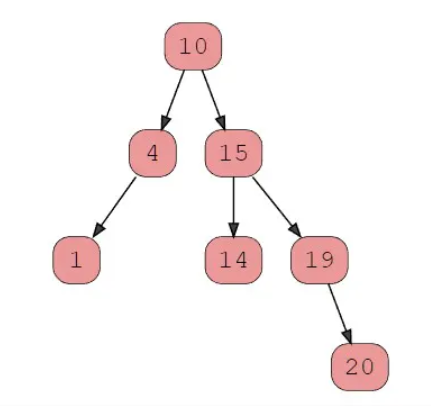
Here is the in-order traversal of this tree: [1, 4, 10, 14, 15, 19, 20]

Here is the expected output from the algorithm based on different calls:

hasNext() -> true

next() -> 1

next() -> 4

hasNext() -> true

next() -> 10

next() -> 14

next() -> 15

next() -> 19

next() -> 20

hasNext() -> false

Constraints:

  • The number of nodes in the tree is in the range [1, 10^5].
  • 0 <= Node.val <= 106
  • At most 105 calls will be made to hasNext, and next.

Solution

A brute force solution could be to store the in-order traversal of the BST in an array and used that array to process the two functions next() and hasNext(). We can maintain a pointer in the array, which points to the next element to be returned to the caller. This algorithm will take O(N) space for storing all elements in the array, and O(N) time to traverse the tree. Both the operations will take O(1) time complexity, as we have pre-processed all the data to store the in-order traversal of the BST in the array.

Transforming a Recursive Algorithm to an Iterative one

We know that we can perform the in-order traversal of a BST recursively. But for the iterator, we can’t use recursion as we can’t stop recursion in the middle to return the required element; this way, we will lose the recursive state of the traversal. Also, we didn’t want to perform the in-order traversal every time next() or hasNext() is called; this will make these function O(N) operations.

We know that we can transform a recursive solution to make it iterative using a stack. This was exactly what we need! This way, we can control the recursion by saving the state of the in-order traversal of the BST in the stack, and later we can resume the tree traversal when next() is called again.

Code

Here is what our algorithm will look like:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
# definition for a binary search tree node
# class TreeNode:
#   def __init__(self, val=0, left=None, right=None):
#     self.val = val
#     self.left = left
#     self.right = right

class Solution:
  def __init__(self, root: TreeNode):
    self.stack = list()
    self.traverse_left(root)

  # returns whether we have a next smallest number
  def hasNext(self):
    return self.stack

  # returns the next smallest number
  def next(self):
    tmpNode = self.stack.pop()
    self.traverse_left(tmpNode.right)
    return tmpNode.val
        
  # traverse the left sub-tree to push all nodes on the stack
  def traverse_left(self, node):
    while node is not None:
      self.stack.append(node)
      node = node.left


def main():
  root = TreeNode(10)
  root.left = TreeNode(4)
  root.left.left = TreeNode(1)
  root.right = TreeNode(15)
  root.right.left = TreeNode(14)
  root.right.right = TreeNode(19)
  root.right.right.right = TreeNode(20)

  sol = Solution(root)
  print("hasNext() -> " + str(bool(sol.hasNext())))
  print("next() -> " + str(sol.next()))
  print("next() -> " + str(sol.next()))
  print("hasNext() -> " + str(bool(sol.hasNext())))
  print("next() -> " + str(sol.next()))
  print("next() -> " + str(sol.next()))
  print("next() -> " + str(sol.next()))
  print("next() -> " + str(sol.next()))
  print("next() -> " + str(sol.next()))
  print("hasNext() -> " + str(bool(sol.hasNext())))


main()

Time Complexity

  • The hasNext() will take O(1) time.
  • Since next() calls the traverseLeft() function which traverses the left subtree and in the worst case the left subtree could contain all elements (practically it would be a list), hence, next() can take O(N) time in the worst case. One thing to note there though, traverseLeft() processes each element only once. This means, amortized cost of traverseLeft() will be O(1) for ‘n’ calls of next(), therefore, next() has O(1) amortized cost.

Space Complexity

We will need O(N) space for the stack in the worst case (when the BST is a list). Overall, we will need to store nodes equal to the height of the tree, hence,
O(H) space complexity, where H is the height of the given tree.

Making the Algorithm Thread Safe

Our algorithm does not have thread-safety. The algorithm would fail if multiple threads access the same BSTIterator object. We could get a synchronization issue in the next() function for the following two lines:

1
2
TreeNode tmpNode = stack.pop();
traverseLeft(tmpNode.right);

If two threads access the function concurrently, the stack could end up in a bad state.

Here is what can happen. Suppose one thread executes the first line to pop an element from the stack. Before it executes the next line (to traverse the left subtree), another thread which is also processing these lines, can also pop another element from the stack, thus, making the stack invalid.

This means we need to synchronize this function so that only one thread is allowed to process next() at any time.

Here is the new synchronized version of the algorithm.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
import multiprocessing

# definition for a binary search tree node
# class TreeNode:
#   def __init__(self, val=0, left=None, right=None):
#     self.val = val
#     self.left = left
#     self.right = right

class Solution:
  def __init__(self, root: TreeNode):
    self.stack = list()
    self.lock = multiprocessing.Lock()
    self.traverse_left(root)

  # returns whether we have a next smallest number
  def hasNext(self):
    return self.stack

  # returns the next smallest number
  def next(self):
    self.lock.acquire()
    tmpNode = self.stack.pop()
    self.traverse_left(tmpNode.right)
    self.lock.release()
    return tmpNode.val
        
  # traverse the left sub-tree to push all nodes on the stack
  def traverse_left(self, node):
    while node is not None:
      self.stack.append(node)
      node = node.left


if __name__ == '__main__':

  root = TreeNode(10)
  root.left = TreeNode(4)
  root.left.left = TreeNode(1)
  root.right = TreeNode(15)
  root.right.left = TreeNode(14)
  root.right.right = TreeNode(19)
  root.right.right.right = TreeNode(20)

  sol = Solution(root)
  print("hasNext() -> " + str(bool(sol.hasNext())))
  print("next() -> " + str(sol.next()))
  print("next() -> " + str(sol.next()))
  print("hasNext() -> " + str(bool(sol.hasNext())))
  print("next() -> " + str(sol.next()))
  print("next() -> " + str(sol.next()))
  print("next() -> " + str(sol.next()))
  print("next() -> " + str(sol.next()))
  print("next() -> " + str(sol.next()))
  print("hasNext() -> " + str(bool(sol.hasNext())))

Making the Algorithm Multi-threaded

To further improve the algorithm, we can make next() multi-threaded so that can return the element to the caller immediately and spawn a separate thread to perform the post-processing required to traverse the left subtree.

In the next() function, we do have the required node available right away, but we could not return to the caller before we traverse the left subtree of the right child of the current node:

1
traverseLeft(tmpNode.right);

we can spawn a new thread to process this traversal and return the element to the caller. This way, the caller is unblocked as it has the data quickly, and all the post-processing is done in a separate thread.

This made the algorithm a bit complex though. Now, whenever we are starting a new execution of next() or hasNext(), we need to ensure any previous thread doing the post-processing has finished. This means that we have to add a check before processing next() or hasNext() to wait and call join() on the previous thread if it has not already finished.

Here is the code that takes care of this scenario:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
import multiprocessing

# definition for a binary search tree node
# class TreeNode:
#   def __init__(self, val=0, left=None, right=None):
#     self.val = val
#     self.left = left
#     self.right = right

class Solution:
  def __init__(self, root: TreeNode):
    self.stack = multiprocessing.Manager().list()
    self.lock = multiprocessing.Lock()
    self.t1 = None
    self.traverse_left(self.stack, root)

  # returns whether we have a next smallest number
  def hasNext(self):
    self.check_thread()
    return self.stack

  # returns the next smallest number
  def next(self):
    self.lock.acquire()
    self.check_thread()
    tmpNode = self.stack.pop()
    self.t1 = multiprocessing.Process(target=self.traverse_left, args=(self.stack, tmpNode.right))
    self.t1.start()
    self.lock.release()
    return tmpNode.val
        
  # traverse the left sub-tree to push all nodes on the stack
  def traverse_left(self, stack, node):
    while node is not None:
      stack.append(node)
      node = node.left
  
  # if the previous thread is active, wait before it finishes
  def check_thread(self):
    if self.t1 is not None and self.t1.is_alive():
        self.t1.join() # wait for the thread traversing the left subtree 


if __name__ == '__main__':

  root = TreeNode(10)
  root.left = TreeNode(4)
  root.left.left = TreeNode(1)
  root.right = TreeNode(15)
  root.right.left = TreeNode(14)
  root.right.right = TreeNode(19)
  root.right.right.right = TreeNode(20)

  sol = Solution(root)
  print("hasNext() -> " + str(bool(sol.hasNext())))
  print("next() -> " + str(sol.next()))
  print("next() -> " + str(sol.next()))
  print("hasNext() -> " + str(bool(sol.hasNext())))
  print("next() -> " + str(sol.next()))
  print("next() -> " + str(sol.next()))
  print("next() -> " + str(sol.next()))
  print("next() -> " + str(sol.next()))
  print("next() -> " + str(sol.next()))
  print("hasNext() -> " + str(bool(sol.hasNext())))

Time and Space Complexities

Everything has the same complexity as the previous solution.

Author：Hasuer

Link：https://hasuer.github.io/28-pattern-multi-thread/index.html

Publish date：May 28th 2024, 2:34:14 pm

Update date：May 28th 2024, 11:31:31 am

License：本文采用知识共享署名-非商业性使用 4.0 国际许可协议进行许可

CATALOG
  1. 1. Introduction to Multi-threaded Pattern
  2. 2. Same Tree
    1. 2.1. Problem Statement
    2. 2.2. Solution
    3. 2.3. Code
    4. 2.4. Making the Algorithm Multi-threaded
    5. 2.5. Time and Space Complexities
  3. 3. Invert Binary Tree
    1. 3.1. Problem Statement
    2. 3.2. Solution
    3. 3.3. Code
    4. 3.4. Time Complexity
    5. 3.5. Space Complexity
    6. 3.6. Making the Algorithm Multi-threaded
    7. 3.7. Time and Space Complexities
  4. 4. Binary Search Tree Iterator
    1. 4.1. Problem Statement
    2. 4.2. Solution
    3. 4.3. Transforming a Recursive Algorithm to an Iterative one
    4. 4.4. Code
    5. 4.5. Time Complexity
    6. 4.6. Space Complexity
    7. 4.7. Making the Algorithm Thread Safe
    8. 4.8. Making the Algorithm Multi-threaded
    9. 4.9. Time and Space Complexities
Total : 41
2024
2022
2021
Interview
技术笔记 Grokking-Interview-Pattern