Hasuer's Studio.

18. Pattern Top 'K' Elements

Grokking Interview Pattern Interview
Word count: 9.2kReading time: 55 min
2024/05/18

Introduction

Any problem that asks us to find the top/smallest/frequent ‘K’ elements among a given set falls under this pattern.

The best data structure that comes to mind to keep track of ‘K’ elements is Heap). This pattern will make use of the Heap to solve multiple problems dealing with ‘K’ elements at a time from a set of given elements.

Let’s jump onto our first problem to develop an understanding of this pattern.

1
2
3
4
5
6
做这种pattern的题目有三种方式
# 1. 先全部塞进去，最后在弹出指定数量作为答案，这样可以保证相同的排序条件，先进去的被取出来
# 2. 先塞进去指定数量，然后每满足条件就替换，如果排序条件已经存在（带比较的数的条件和heap[0]的条件一样），那就不会替换，这样
#    也可以保证答案中会优先包含先进去的数
# 3. 每塞进去一个就判断是不是已经超过了指定长度，如果超过了就弹出一个，这样就会导致相同的排序条件，会优先保留后进来的，这是我们不想要的。
#    所以这道题选择第一种和第二种是合理的

Top ‘K’ Numbers (easy)

Design Gurus Educative.io

Problem Statement

Given an unsorted array of numbers, find the ‘K’ largest numbers in it.

Note: For a detailed discussion about different approaches to solve this problem, take a look at Kth Smallest Number(这是Miscellaneous类别的）

Example 1:

1
2
Input: [3, 1, 5, 12, 2, 11], K = 3
Output: [5, 12, 11]

Example 2:

1
2
Input: [5, 12, 11, -1, 12], K = 3
Output: [12, 11, 12]

Constraints:

  • 1 <= nums.length <= 10^5
  • -10^5 <= nums[i] <= 10^5
  • k is in the range [1, the number of unique elements in the array].
  • It is guaranteed that the answer is unique.

Solution

A brute force solution could be to sort the array and return the largest K numbers. The time complexity of such an algorithm will be O(N\logN)* as we need to use a sorting algorithm like Timsort if we use Java’s Collection.sort(). Can we do better than that?

The best data structure that comes to mind to keep track of top ‘K’ elements is Heap). Let’s see if we can use a heap to find a better algorithm.

If we iterate through the array one element at a time and keep ‘K’ largest numbers in a heap such that each time we find a larger number than the smallest number in the heap, we do two things:

  1. Take out the smallest number from the heap, and
  2. Insert the larger number into the heap.

This will ensure that we always have ‘K’ largest numbers in the heap. The most efficient way to repeatedly find the smallest number among a set of numbers will be to use a min-heap. As we know, we can find the smallest number in a min-heap in constant time O(1), since the smallest number is always at the root of the heap. Extracting the smallest number from a min-heap will take O(logN) (if the heap has ‘N’ elements) as the heap needs to readjust after the removal of an element.

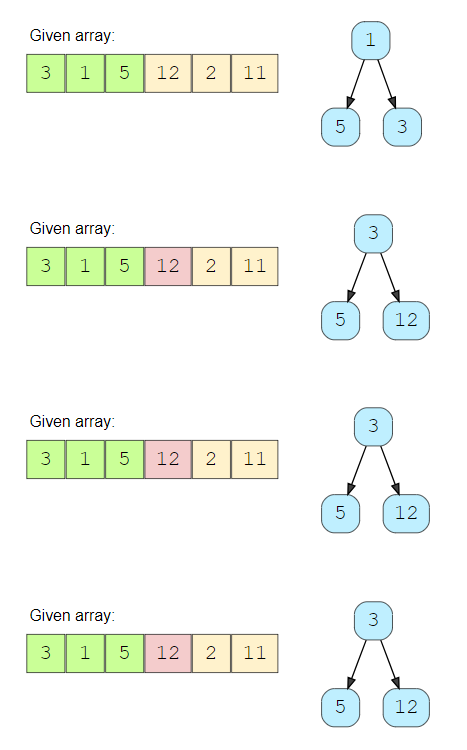
Let’s take Example-1 to go through each step of our algorithm:

Given array: [3, 1, 5, 12, 2, 11], and K=3

  1. First, let’s insert ‘K’ elements in the min-heap.
  2. After the insertion, the heap will have three numbers [3, 1, 5] with ‘1’ being the root as it is the smallest element.
  3. We’ll iterate through the remaining numbers and perform the above-mentioned two steps if we find a number larger than the root of the heap.
  4. The 4th number is ‘12’ which is larger than the root (which is ‘1’), so let’s take out ‘1’ and insert ‘12’. Now the heap will have [3, 5, 12] with ‘3’ being the root as it is the smallest element.
  5. The 5th number is ‘2’ which is not bigger than the root of the heap (‘3’), so we can skip this as we already have top three numbers in the heap.
  6. The last number is ‘11’ which is bigger than the root (which is ‘3’), so let’s take out ‘3’ and insert ‘11’. Finally, the heap has the largest three numbers: [5, 12, 11]

As discussed above, it will take us O(logK) to extract the minimum number from the min-heap. So the overall time complexity of our algorithm will be O(K\logK+(N-K)*logK)* since, first, we insert ‘K’ numbers in the heap and then iterate through the remaining numbers and at every step, in the worst case, we need to extract the minimum number and insert a new number in the heap. This algorithm is better than O(N\logN)*.

Here is the visual representation of our algorithm:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
from heapq import *

class Solution:
  def findKLargestNumbers(self, nums, k):
    minHeap = []
    # put first 'K' numbers in the min heap
    for i in range(k):
      heappush(minHeap, nums[i])

    # go through the remaining numbers of the array, if the number from the array is 
    # bigger than the top(smallest) number of the min-heap, remove the top number from 
    # heap and add the number from array
    for i in range(k, len(nums)):
      if nums[i] > minHeap[0]:
        heappop(minHeap)
        heappush(minHeap, nums[i])

    # the heap has the top 'K' numbers
    return minHeap


def main():
  sol = Solution()
  print("Here are the top K numbers: " +
        str(sol.findKLargestNumbers([3, 1, 5, 12, 2, 11], 3)))

  print("Here are the top K numbers: " +
        str(sol.findKLargestNumbers([5, 12, 11, -1, 12], 3)))


main()

Time complexity

As discussed above, the time complexity of this algorithm is O(KlogK+(N-K)logK), which is asymptotically equal to O(NlogK)

Space complexity

The space complexity will be O(K) since we need to store the top ‘K’ numbers in the heap.

Kth Smallest Number (easy)

Top Interview 150 | 215. Kth Largest Element in an Array Design Gurus Educative.io

Problem Statement

Given an unsorted array of numbers, find Kth smallest number in it.

Please note that it is the Kth smallest number in the sorted order, not the Kth distinct element.

Note: For a detailed discussion about different approaches to solve this problem, take a look at Kth Smallest Number.

Example 1:

1
2
3
Input: [1, 5, 12, 2, 11, 5], K = 3
Output: 5
Explanation: The 3rd smallest number is '5', as the first two smaller numbers are [1, 2].

Example 2:

1
2
3
Input: [1, 5, 12, 2, 11, 5], K = 4
Output: 5
Explanation: The 4th smallest number is '5', as the first three small numbers are [1, 2, 5].

Example 3:

1
2
3
Input: [5, 12, 11, -1, 12], K = 3
Output: 11
Explanation: The 3rd smallest number is '11', as the first two small numbers are [5, -1].

Constraints:

  • 1 <= k <= nums.length <= 10^5
  • -10^4 <= nums[i] <= 10^4

Solution

This problem follows the Top ‘K’ Numbers pattern but has two differences:

  1. Here we need to find the Kth smallest number, whereas in Top ‘K’ Numbers we were dealing with ‘K’ largest numbers.
  2. In this problem, we need to find only one number (Kth smallest) compared to finding all ‘K’ largest numbers.

We can follow the same approach as discussed in the ‘Top K Elements’ problem. To handle the first difference mentioned above, we can use a max-heap instead of a min-heap. As we know, the root is the biggest element in the max heap. So, since we want to keep track of the ‘K’ smallest numbers, we can compare every number with the root while iterating through all numbers, and if it is smaller than the root, we’ll take the root out and insert the smaller number.

Code

Here is what our algorithm will look like:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
from heapq import *

class Solution:
  def findKthSmallestNumber(self, nums, k):
    maxHeap = []
    # put first k numbers in the max heap
    for i in range(k):
      heappush(maxHeap, -nums[i])

    # go through the remaining numbers of the array, if the number from the array is 
    # smaller than the top(biggest) number of the heap, remove the top number from heap 
    # and add the number from array
    for i in range(k, len(nums)):
      if -nums[i] > maxHeap[0]:
        heappop(maxHeap)
        heappush(maxHeap, -nums[i])

    # the root of the heap has the Kth smallest number
    return -maxHeap[0]


def main():
  sol = Solution()
  print("Kth smallest number is: " +
        str(sol.findKthSmallestNumber([1, 5, 12, 2, 11, 5], 3)))

  # since there are two 5s in the input array, our 3rd and 4th smallest numbers should 
  # be a '5'
  print("Kth smallest number is: " +
        str(sol.findKthSmallestNumber([1, 5, 12, 2, 11, 5], 4)))

  print("Kth smallest number is: " +
        str(sol.findKthSmallestNumber([5, 12, 11, -1, 12], 3)))


main()

Time complexity

The time complexity of this algorithm is O(KlogK+(N-K)logK), which is asymptotically equal to O(N\logK)*

Space complexity

The space complexity will be O(K) because we need to store ‘K’ smallest numbers in the heap.

An Alternate Approach

Alternatively, we can use a Min Heap to find the Kth smallest number. We can insert all the numbers in the min-heap and then extract the top ‘K’ numbers from the heap to find the Kth smallest number. Initializing the min-heap with all numbers will take O(N) and extracting ‘K’ numbers will take O(KlogN). Overall, the time complexity of this algorithm will be O(N+KlogN) and the space complexity will be O(N).

‘K’ Closest Points to the Origin (easy)

973. K Closest Points to Origin Design Gurus Educative.io

Problem Statement

Given an array of points in the a 2D plane, find ‘K’ closest points to the origin.

Example 1:

1
2
3
4
5
Input: points = [[1,2],[1,3]], K = 1
Output: [[1,2]]
Explanation: The Euclidean distance between (1, 2) and the origin is sqrt(5).
The Euclidean distance between (1, 3) and the origin is sqrt(10).
Since sqrt(5) < sqrt(10), therefore (1, 2) is closer to the origin.

Example 2:

1
2
Input: point = [[1, 3], [3, 4], [2, -1]], K = 2
Output: [[1, 3], [2, -1]]

Constraints:

  • 1 <= k <= points.length <= 10^4
  • -10^4 <= xi, yi <= 10^4

Solution

The Euclidean distance of a point P(x,y) from the origin can be calculated through the following formula:

\sqrt{x^2 + y^2}√x2+y2

This problem follows the Top ‘K’ Numbers pattern. The only difference in this problem is that we need to find the closest point (to the origin) as compared to finding the largest numbers.

Following a similar approach, we can use a Max Heap to find ‘K’ points closest to the origin. While iterating through all points, if a point (say ‘P’) is closer to the origin than the top point of the max-heap, we will remove that top point from the heap and add ‘P’ to always keep the closest points in the heap.

Code

Here is what our algorithm will look like:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
# 如果要构造kth closest的point,也是构造大顶堆，只不过返回的时候返回第一个就可以
# 如果要构造kth farest的point, 就要构造小顶堆，返回的时候返回第一个就可以，越小的排在越前面，def __lt__(self, other)中就要改成return self.distance_from_origin() < other.distance_from_origin()

from heapq import *

# class Point:

  # def __init__(self, x, y):
  #   self.x = x
  #   self.y = y

  # # Define a custom comparison method for max-heap.
  # def __lt__(self, other):
  #   return self.distance_from_origin() > other.distance_from_origin()

  # def distance_from_origin(self):
  #   # Calculate the distance from the origin (squared for comparison).
  #   return (self.x * self.x) + (self.y * self.y)

class Solution:
  def findClosestPoints(self, points, k):
    maxHeap = []
    
    # Initialize the max-heap with the first 'k' points.
    for i in range(k):
      heappush(maxHeap, (-points[i].distance_from_origin(), points[i]))

    for i in range(k, len(points)):
      distance = points[i].distance_from_origin()
      
      # If the current point is closer to the origin than the farthest point in max-heap, replace it.
      if distance < -maxHeap[0][0]:
        heappop(maxHeap)
        heappush(maxHeap, (-distance, points[i]))

    closestPoints = []
    
    # Extract the closest points from the max-heap.
    while maxHeap:
      closestPoints.append(maxHeap[0][1])
      heappop(maxHeap)

    return closestPoints
  
  @staticmethod
  def print_point(point):
    print("[" + str(point.x) + ", " + str(point.y) + "] ", end='')

def main():
  sol = Solution()
  result = sol.findClosestPoints([Point(1, 3), Point(3, 4), Point(2, -1)], 2)
  print("Here are the k points closest to the origin: ", end='')
  for point in result:
    Solution.print_point(point)  # Call the static method correctly


main()

    
# ==================================leetcode======================================
class Solution(object):
    def distance_from_origin(self, point):
        return pow(point[0], 2) + pow(point[1], 2)

    def kClosest(self, points, k):
        """
        :type points: List[List[int]]
        :type k: int
        :rtype: List[List[int]]
        """
        max_heap = []
        for i in range(k):
            heappush(max_heap, (-self.distance_from_origin(points[i]), points[i]))
        for i in range(k, len(points)):
            if self.distance_from_origin(points[i]) < self.distance_from_origin(max_heap[0][1]):
                heappop(max_heap)
                heappush(max_heap, (-self.distance_from_origin(points[i]), points[i]))
        res =[]
        while max_heap:
            res.append(heappop(max_heap)[1])
        return res

Time complexity

The time complexity of this algorithm is (N\logK)* as we iterating all points and pushing them into the heap.

Space complexity

The space complexity will be O(K) because we need to store ‘K’ point in the heap.

Connect Ropes (easy)

Leetcode 1167 会员 Design Gurus Educative.io

Problem Statement

Given ‘N’ ropes with different lengths, we need to connect these ropes into one big rope with minimum cost. The cost of connecting two ropes is equal to the sum of their lengths.

Example 1:

1
2
3
Input: [1, 3, 11, 5]
Output: 33
Explanation: First connect 1+3(=4), then 4+5(=9), and then 9+11(=20). So the total cost is 33 (4+9+20)

Example 2:

1
2
3
Input: [3, 4, 5, 6]
Output: 36
Explanation: First connect 3+4(=7), then 5+6(=11), 7+11(=18). Total cost is 36 (7+11+18)

Example 3:

1
2
3
Input: [1, 3, 11, 5, 2]
Output: 42
Explanation: First connect 1+2(=3), then 3+3(=6), 6+5(=11), 11+11(=22). Total cost is 42 (3+6+11+22)

Constraints:

  • 1 <= ropLengths.length <= 10^4
  • 1 <= ropLengths[i] <= 10^4

Solution

In this problem, following a greedy approach to connect the smallest ropes first will ensure the lowest cost. We can use a Min Heap to find the smallest ropes following a similar approach as discussed in Kth Smallest Number. Once we connect two ropes, we need to insert the resultant rope back in the Min Heap so that we can connect it with the remaining ropes.

Code

Here is what our algorithm will look like:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
from heapq import *

class Solution:
  def minimumCostToConnectRopes(self, ropeLengths):
    minHeap = []
    # add all ropes to the min heap
    for i in ropeLengths:
      heappush(minHeap, i)

    # go through the values of the heap, in each step take top (lowest) rope lengths from 
    # the min heap connect them and push the result back to the min heap.
    # keep doing this until the heap is left with only one rope
    result, temp = 0, 0
    while len(minHeap) > 1:
      temp = heappop(minHeap) + heappop(minHeap)
      result += temp
      heappush(minHeap, temp)

    return result


def main():
  sol = Solution()
  print("Minimum cost to connect ropes: " +
        str(sol.minimumCostToConnectRopes([1, 3, 11, 5])))
  print("Minimum cost to connect ropes: " +
        str(sol.minimumCostToConnectRopes([3, 4, 5, 6])))
  print("Minimum cost to connect ropes: " +
        str(sol.minimumCostToConnectRopes([1, 3, 11, 5, 2])))

main()

Time complexity

Given ‘N’ ropes, we need O(N\logN)* to insert all the ropes in the heap. In each step, while processing the heap, we take out two elements from the heap and insert one. This means we will have a total of ‘N’ steps, having a total time complexity of O(N\logN)*.

Space complexity

The space complexity will be O(N) because we need to store all the ropes in the heap.

Top ‘K’ Frequent Numbers (medium)

347. Top K Frequent Elements Design Gurus Educative.io

Problem Statement

Given an unsorted array of numbers, find the top ‘K’ frequently occurring numbers in it.

Example 1:

1
2
3
Input: [1, 3, 5, 12, 11, 12, 11], K = 2
Output: [12, 11]
Explanation: Both '11' and '12' apeared twice.

Example 2:

1
2
3
Input: [5, 12, 11, 3, 11], K = 2
Output: [11, 5] or [11, 12] or [11, 3]
Explanation: Only '11' appeared twice, all other numbers appeared once.

Constraints:

  • 1 <= nums.length <= 10^5
  • -10^5 <= nums[i] <= 10^5
  • k is in the range [1, the number of unique elements in the array].
  • It is guaranteed that the answer is unique.

Solution

This problem follows Top ‘K’ Numbers. The only difference is that in this problem, we need to find the most frequently occurring number compared to finding the largest numbers.

We can follow the same approach as discussed in the Top K Elements problem. However, in this problem, we first need to know the frequency of each number, for which we can use a HashMap. Once we have the frequency map, we can use a Min Heap to find the ‘K’ most frequently occurring number. In the Min Heap, instead of comparing numbers we will compare their frequencies in order to get frequently occurring numbers

Code

Here is what our algorithm will look like:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
from heapq import *


class Solution:
    def findTopKFrequentNumbers(self, nums, k):

        # find the frequency of each number
        numFrequencyMap = {}
        for num in nums:
            numFrequencyMap[num] = numFrequencyMap.get(num, 0) + 1

        minHeap = []
        # 2024.4.12 note: 建议使用方法1：先全部塞进去在去除前面的n-k个，理由见“'K' Closest Numbers”这道题，因为要是像这样写，答案就会不唯一，不过这道题的
        # example中允许有不唯一的时候输出其中任何一个就可以，所以问题不大
        # go through all numbers of the numFrequencyMap and push them in the minHeap, which
        # will have top k frequent numbers. If the heap size is more than k, we remove the
        # smallest(top) number
        for num, frequency in numFrequencyMap.items():
            heappush(minHeap, (frequency, num))
            # 2024.4.11 note:可以使用方法2：像之前一样，先push k 个，然后新的比heap[0]大的话，就替换heap[0]，但是在这个例子就比较麻烦
            if len(minHeap) > k:
                heappop(minHeap)


        # create a list of top k numbers
        topNumbers = []
        while minHeap:
            topNumbers.append(heappop(minHeap)[1])

        return topNumbers


def main():
    sol = Solution()
    print("Here are the K frequent numbers: " +
          str(sol.findTopKFrequentNumbers([1, 3, 5, 12, 11, 12, 11], 2)))

    print("Here are the K frequent numbers: " +
          str(sol.findTopKFrequentNumbers([5, 12, 11, 3, 11], 2)))


main()

Time complexity

The time complexity of the above algorithm is O(N+N\logK)*.

Space complexity

The space complexity will be O(N). Even though we are storing only ‘K’ numbers in the heap. For the frequency map, however, we need to store all the ‘N’ numbers.

Frequency Sort (medium)

451. Sort Characters By Frequency Design Gurus Educative.io

Problem Statement

Given a string, sort it based on the decreasing frequency of its characters.

Example 1:

1
2
3
Input: "Programming"
Output: "rrggmmPiano"
Explanation: 'r', 'g', and 'm' appeared twice, so they need to appear before any other character.

Example 2:

1
2
3
Input: "abcbab"
Output: "bbbaac"
Explanation: 'b' appeared three times, 'a' appeared twice, and 'c' appeared only once.

Constraints:

  • 1 <= str.length <= 5 * 10^5
  • str consists of uppercase and lowercase English letters and digits.

Solution

This problem follows the Top ‘K’ Elements pattern, and shares similarities with Top ‘K’ Frequent Numbers.

We can follow the same approach as discussed in the Top ‘K’ Frequent Numbers problem. First, we will find the frequencies of all characters, then use a max-heap to find the most occurring characters.

Code

Here is what our algorithm will look like:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
from heapq import *


class Solution:
    def sortCharacterByFrequency(self, str):

        # find the frequency of each character
        charFrequencyMap = {}
        for char in str:
            charFrequencyMap[char] = charFrequencyMap.get(char, 0) + 1

        maxHeap = []
        # 这个就是方法1， 先全部塞进去，这样就可以保证，相同的排序条件（这题中是频数），先出现的字母会依旧在前面
        # add all characters to the max heap
        for char, frequency in charFrequencyMap.items():
            heappush(maxHeap, (-frequency, char))

        # build a string, appending the most occurring characters first
        sortedString = []
        while maxHeap:
            frequency, char = heappop(maxHeap)
            for _ in range(-frequency):
                sortedString.append(char)

        return ''.join(sortedString)


def main():
    sol = Solution()
    print("String after sorting characters by frequency: " +
          sol.sortCharacterByFrequency("Programming"))
    print("String after sorting characters by frequency: " +
          sol.sortCharacterByFrequency("abcbab"))


main()

Time complexity

The time complexity of the above algorithm is O(D\logD)* where ‘D’ is the number of distinct characters in the input string. This means, in the worst case, when all characters are unique the time complexity of the algorithm will be O(N\logN)* where ‘N’ is the total number of characters in the string.

Space complexity

The space complexity will be O(N), as in the worst case, we need to store all the ‘N’ characters in the HashMap.

Kth Largest Number in a Stream (medium)

leetcode 703 一样的代码，leetcode报错，感觉是leetcode内部问题

703. Kth Largest Element in a Stream Design Gurus Educative.io

Problem Statement

Design a class to efficiently find the Kth largest element in a stream of numbers.

The class should have the following two things:

  1. The constructor of the class should accept an integer array containing initial numbers from the stream and an integer ‘K’.
  2. The class should expose a function add(int num) which will store the given number and return the Kth largest number.

Example 1:

1
2
3
4
5
Input: [3, 1, 5, 12, 2, 11], K = 4
1. Calling add(6) should return '5'.
2. Calling add(13) should return '6'.
2. Calling add(4) should still return '6'.

Constraints:

  • 1 <= k <= 10^4
  • 0 <= nums.length <= 10^4
  • -10^4 <= nums[i] <= 10^4
  • -10^4 <= val <= 10^4
  • At most 10^4 calls will be made to add.
  • It is guaranteed that there will be at least k elements in the array when you search for the kth element.

Solution

This problem follows the Top ‘K’ Elements pattern and shares similarities with Kth Smallest number.

We can follow the same approach as discussed in the ‘Kth Smallest number’ problem. However, we will use a Min Heap (instead of a Max Heap) as we need to find the Kth largest number.

Code

Here is what our algorithm will look like:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
from heapq import *


class Solution:

  def __init__(self, nums, k):
    self.minHeap = []
    self.k = k
    # add the numbers in the min heap
    for num in nums:
      self.add(num)

  def add(self, num):
    # add the new number in the min heap
    heappush(self.minHeap, num)

    # if heap has more than 'k' numbers, remove one number
    if len(self.minHeap) > self.k:
      heappop(self.minHeap)

    # return the 'Kth largest number
    return self.minHeap[0]



def main():

  sol = Solution([3, 1, 5, 12, 2, 11], 4)
  print("4th largest number is: " + str(sol.add(6)))
  print("4th largest number is: " + str(sol.add(13)))
  print("4th largest number is: " + str(sol.add(4)))


main()

Time complexity

The time complexity of the add() function will be O(logK) since we are inserting the new number in the heap.

Space complexity

The space complexity will be O(K) for storing numbers in the heap.

‘K’ Closest Numbers (medium)

658. Find K Closest Elements Design Gurus Educative.io

Problem Statement

Given a sorted number array and two integers ‘K’ and ‘X’, find ‘K’ closest numbers to ‘X’ in the array. Return the numbers in the sorted order. ‘X’ is not necessarily present in the array.

Example 1:

1
2
Input: [5, 6, 7, 8, 9], K = 3, X = 7
Output: [6, 7, 8]

Example 2:

1
2
Input: [2, 4, 5, 6, 9], K = 3, X = 6
Output: [4, 5, 6]

Example 3:

1
2
Input: [2, 4, 5, 6, 9], K = 3, X = 10
Output: [5, 6, 9]

Solution

This problem follows the Top ‘K’ Numbers pattern. The biggest difference in this problem is that we need to find the closest (to ‘X’) numbers compared to finding the overall largest numbers. Another difference is that the given array is sorted.

Utilizing a similar approach, we can find the numbers closest to ‘X’ through the following algorithm:

  1. Since the array is sorted, we can first find the number closest to ‘X’ through Binary Search. Let’s say that number is ‘Y’（Y不需要一定是最接近的，如果arr中不存在x,那么只要是x的左右邻居就可以）.
  2. The ‘K’ closest numbers to ‘Y’ will be adjacent to ‘Y’ in the array. We can search in both directions of ‘Y’ to find the closest numbers.
  3. We can use a heap to efficiently search for the closest numbers. We will take ‘K’ numbers in both directions of ‘Y’ and push them in a Min Heap sorted by their absolute difference from ‘X’. This will ensure that the numbers with the smallest difference from ‘X’ (i.e., closest to ‘X’) can be extracted easily from the Min Heap.
  4. Finally, we will extract the top ‘K’ numbers from the Min Heap to find the required numbers.

Code

Here is what our algorithm will look like:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
from heapq import *


class Solution:
    def findClosestElements(self, arr, K, X):
        index = self.binary_search(arr, X)
        low, high = index - K, index + K

        low = max(low, 0)  # 'low' should not be less than zero
        # 'high' should not be greater the size of the array
        high = min(high, len(arr) - 1)

        minHeap = []
        # add all candidate elements to the min heap, sorted by their absolute difference
        # from 'X'
        for i in range(low, high + 1):
            heappush(minHeap, (abs(arr[i] - X), arr[i]))

        # we need the top 'K' elements having smallest difference from 'X'
        result = []
        for _ in range(K):
            result.append(heappop(minHeap)[1])

        result.sort()
        return result

    def binary_search(self, arr, target):
        low, high = 0, len(arr) - 1
        while low <= high:
            mid = int(low + (high - low) / 2)
            if arr[mid] == target:
                return mid
            if arr[mid] < target:
                low = mid + 1
            else:
                high = mid - 1
        # 如果不存在这个的话，如果end != -1 and low != len(arr), 那么arr[high] < target < arr[low]
        if high < 0:
            return low
        else:
            return high


def main():
    sol = Solution()
    print("'K' closest numbers to 'X' are: " +
          str(sol.findClosestElements([5, 6, 7, 8, 9], 3, 7)))
    print("'K' closest numbers to 'X' are: " +
          str(sol.findClosestElements([2, 4, 5, 6, 9], 3, 6)))
    print("'K' closest numbers to 'X' are: " +
          str(sol.findClosestElements([2, 4, 5, 6, 9], 3, 10)))


main()

Time complexity

The time complexity of the above algorithm is O(logN + K\logK)*. We need O(logN) for Binary Search and O(K\logK)* to insert the numbers in the Min Heap, as well as to sort the output array.

Space complexity

The space complexity will be O(K), as we need to put a maximum of 2K numbers in the heap.

Alternate Solution using Two Pointers

After finding the number closest to ‘X’ through Binary Search, we can use the Two Pointers approach to find the ‘K’ closest numbers. Let’s say the closest number is ‘Y’. We can have a left pointer to move back from ‘Y’ and a right pointer to move forward from ‘Y’. At any stage, whichever number pointed out by the left or the right pointer gives the smaller difference from ‘X’ will be added to our result list.

To keep the resultant list sorted we can use a Queue. So whenever we take the number pointed out by the left pointer, we will append it at the beginning of the list and whenever we take the number pointed out by the right pointer we will append it at the end of the list.

Here is what our algorithm will look like:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
from collections import deque


class Solution:
    def findClosestElements(self, arr, K, X):
        result = deque()

        # Binary search to find the index of the element closest to X
        index = self.binary_search(arr, X)
        # 如果不存在x,返回的index是x左边的那个数的index(index >=0的时候)
        # 不然就是end，e.g. arr = [2,4,5,7], x = 1
        leftPointer, rightPointer = index, index + 1
        n = len(arr)

        for i in range(K):
            # Check if there are elements on both sides of the chosen element
            if leftPointer >= 0 and rightPointer < n:
                diff1 = abs(X - arr[leftPointer])
                diff2 = abs(X - arr[rightPointer])

                # Choose the element with the smaller absolute difference
                if diff1 <= diff2:  # 这里的等于很重要，因为如果排序条件一样，优先返回左边的
                    result.appendleft(arr[leftPointer])  # Add the left element to the result
                    leftPointer -= 1
                else:
                    result.append(arr[rightPointer])  # Add the right element to the result
                    rightPointer += 1
            # If there are no elements on one side, add elements from the other side
            elif leftPointer >= 0:  # 优先left
                result.appendleft(arr[leftPointer])
                leftPointer -= 1
            elif rightPointer < n:
                result.append(arr[rightPointer])
                rightPointer += 1

        return result

    # Binary search method to find the index of the closest element to the target
    def binary_search(self, arr, target):
        low, high = 0, len(arr) - 1
        while low <= high:
            mid = int(low + (high - low) / 2)
            if arr[mid] == target:
                return mid
            if arr[mid] < target:
                low = mid + 1
            else:
                high = mid - 1
        # 如果不存在这个的话，如果end != -1 and low != len(arr), 那么arr[high] < target < arr[low]
        if high < 0:
            return low
        else:
            return high


def main():
    sol = Solution()
    print("'K' closest numbers to 'X' are: " +
          str(sol.findClosestElements([5, 6, 7, 8, 9], 3, 7)))
    print("'K' closest numbers to 'X' are: " +
          str(sol.findClosestElements([2, 4, 5, 6, 9], 3, 6)))
    print("'K' closest numbers to 'X' are: " +
          str(sol.findClosestElements([2, 4, 5, 6, 9], 3, 10)))


main()

Time complexity

The time complexity of the above algorithm is O(logN + K). We need O(logN) for Binary Search and O(K) for finding the ‘K’ closest numbers using the two pointers.

Space complexity

If we ignoring the space required for the output list, the algorithm runs in constant space O(1).

Maximum Distinct Elements (medium)

Similar | 题目意思怪怪的，看例子也不是标题中的unique | 1481. Least Number of Unique Integers after K Removals Design Gurus Educative.io

Problem Statement

Given an array of numbers and a number ‘K’, we need to remove ‘K’ numbers from the array such that we are left with maximum distinct numbers.

Example 1:

1
2
3
4
5
6
Input: [7, 3, 5, 8, 5, 3, 3], and K=2
Output: 3
Explanation: We can remove two occurrences of 3 to be left with 3 distinct numbers [7, 3, 8], we have 
to skip 5 because it is not distinct and occurred twice. 
Another solution could be to remove one instance of '5' and '3' each to be left with three 
distinct numbers [7, 5, 8], in this case, we have to skip 3 because it occurred twice.

Example 2:

1
2
3
4
Input: [3, 5, 12, 11, 12], and K=3
Output: 2
Explanation: We can remove one occurrence of 12, after which all numbers will become distinct. Then 
we can delete any two numbers which will leave us 2 distinct numbers in the result.

Example 3:

1
2
3
Input: [1, 2, 3, 3, 3, 3, 4, 4, 5, 5, 5], and K=2
Output: 3
Explanation: We can remove one occurrence of '4' to get three distinct numbers.

Constraints:

  • 1 <= arr.length <= 10^5
  • 1 <= arr[i] <= 10^9
  • 0 <= k <= arr.length

Solution

This problem follows the Top ‘K’ Numbers pattern, and shares similarities with Top ‘K’ Frequent Numbers.

We can following a similar approach as discussed in Top ‘K’ Frequent Numbers problem:

  1. First, we will find the frequencies of all the numbers.
  2. Then, push all numbers that are not distinct (i.e., have a frequency higher than one) in a Min Heap based on their frequencies. At the same time, we will keep a running count of all the distinct numbers.
  3. Following a greedy approach, in a stepwise fashion, we will remove the least frequent number from the heap (i.e., the top element of the min-heap), and try to make it distinct. We will see if we can remove all occurrences of a number except one. If we can, we will increment our running count of distinct numbers. We have to also keep a count of how many removals we have done.
  4. If after removing elements from the heap, we are still left with some deletions, we have to remove some distinct elements.

Code

Here is what our algorithm will look like:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
from heapq import *

class Solution:
  def findMaximumDistinctElements(self, nums, k):
    distinctElementsCount = 0
    if len(nums) <= k:
      return distinctElementsCount

    # find the frequency of each number
    numFrequencyMap = {}
    for i in nums:
      numFrequencyMap[i] = numFrequencyMap.get(i, 0) + 1

    minHeap = []
    # insert all numbers with frequency greater than '1' into the min-heap
    for num, frequency in numFrequencyMap.items():
      if frequency == 1:
        distinctElementsCount += 1
      else:
        heappush(minHeap, (frequency, num))

    # following a greedy approach, try removing the least frequent numbers first from 
    # the min-heap
    while k > 0 and minHeap:
      frequency, num = heappop(minHeap)
      # to make an element distinct, we need to remove all of its occurrences except one
      k -= frequency - 1
      if k >= 0:
        distinctElementsCount += 1

    # if k > 0, this means we have to remove some distinct numbers
    if k > 0:
      distinctElementsCount -= k

    return distinctElementsCount


def main():
  sol = Solution()
  print("Maximum distinct numbers after removing K numbers: " +
        str(sol.findMaximumDistinctElements([7, 3, 5, 8, 5, 3, 3], 2)))
  print("Maximum distinct numbers after removing K numbers: " +
        str(sol.findMaximumDistinctElements([3, 5, 12, 11, 12], 3)))
  print("Maximum distinct numbers after removing K numbers: " +
        str(sol.findMaximumDistinctElements([1, 2, 3, 3, 3, 3, 4, 4, 5, 5, 5], 2)))


main()

Time complexity

Since we will insert all numbers in a HashMap and a Min Heap, this will take O(N\logN)* where ‘N’ is the total input numbers. While extracting numbers from the heap, in the worst case, we will need to take out ‘K’ numbers. This will happen when we have at least ‘K’ numbers with a frequency of two. Since the heap can have a maximum of ‘N/2’ numbers, therefore, extracting an element from the heap will take O(logN) and extracting ‘K’ numbers will take O(KlogN). So overall, the time complexity of our algorithm will be O(N\logN + KlogN)*.

We can optimize the above algorithm and only push ‘K’ elements in the heap, as in the worst case we will be extracting ‘K’ elements from the heap. This optimization will reduce the overall time complexity to O(N\logK + KlogK)*.

Space complexity

The space complexity will be O(N) as, in the worst case, we need to store all the ‘N’ characters in the HashMap.

Sum of Elements (medium)

Design Gurus Educative.io

Problem Statement

Given an array, find the sum of all numbers between the K1’th and K2’th smallest elements of that array.

Example 1:

1
2
3
4
Input: [1, 3, 12, 5, 15, 11], and K1=3, K2=6
Output: 23
Explanation: The 3rd smallest number is 5 and 6th smallest number 15. The sum of numbers coming
between 5 and 15 is 23 (11+12).

Example 2:

1
2
3
4
Input: [3, 5, 8, 7], and K1=1, K2=4
Output: 12
Explanation: The sum of the numbers between the 1st smallest number (3) and the 4th smallest 
number (8) is 12 (5+7).

Solution

This problem follows the Top ‘K’ Numbers pattern, and shares similarities with Kth Smallest Number.

We can find the sum of all numbers coming between the K1’th and K2’th smallest numbers in the following steps:

  1. First, insert all numbers in a min-heap.
  2. Remove the first K1 smallest numbers from the min-heap.
  3. Now take the next K2-K1-1 numbers out of the heap and add them. This sum will be our required output.

Code

Here is what our algorithm will look like:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
# 直观想到的就是直接sort排序，时间复杂度也是nlogn
from heapq import *

class Solution:
  def findSumOfElements(self, nums, k1, k2):
    minHeap = []
    # insert all numbers to the min heap
    for num in nums:
      heappush(minHeap, num)

    # remove k1 small numbers from the min heap
    for _ in range(k1):
      heappop(minHeap)

    elementSum = 0
    # sum next k2-k1-1 numbers
    for _ in range(k2 - k1 - 1):
      elementSum += heappop(minHeap)

    return elementSum


def main():
  sol = Solution()
  print("Sum of all numbers between k1 and k2 smallest numbers: " +
        str(sol.findSumOfElements([1, 3, 12, 5, 15, 11], 3, 6)))
  print("Sum of all numbers between k1 and k2 smallest numbers: " +
        str(sol.findSumOfElements([3, 5, 8, 7], 1, 4)))


main()

Time complexity

Since we need to put all the numbers in a min-heap, the time complexity of the above algorithm will be O(N\logN)* where ‘N’ is the total input numbers.

Space complexity

The space complexity will be O(N), as we need to store all the ‘N’ numbers in the heap.

Alternate Solution

We can iterate the array and use a max-heap to keep track of the top K2 numbers. We can, then, add the top K2-K1-1 numbers in the max-heap to find the sum of all numbers coming between the K1’th and K2’th smallest numbers. Here is what the algorithm will look like:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
from heapq import *

class Solution:
  def findSumOfElements(self, nums, k1, k2):
    maxHeap = []
    # keep smallest k2 numbers in the max heap
    for i in range(len(nums)):
      if i < k2 - 1:
        heappush(maxHeap, -nums[i])
      elif nums[i] < -maxHeap[0]:
        heappop(maxHeap) # as we are interested only in the smallest k2 numbers
        heappush(maxHeap, -nums[i])

    # get the sum of numbers between k1 and k2 indices
    # these numbers will be at the top of the max heap
    elementSum = 0
    for _ in range(k2 - k1 - 1):
      elementSum += -heappop(maxHeap)

    return elementSum


def main():
  sol = Solution()
  print("Sum of all numbers between k1 and k2 smallest numbers: " +
        str(sol.findSumOfElements([1, 3, 12, 5, 15, 11], 3, 6)))
  print("Sum of all numbers between k1 and k2 smallest numbers: " +
        str(sol.findSumOfElements([3, 5, 8, 7], 1, 4)))


main()

Time complexity

Since we need to put only the top K2 numbers in the max-heap at any time, the time complexity of the above algorithm will be O(N\logK2)*.

Space complexity

The space complexity will be O(K2), as we need to store the smallest ‘K2’ numbers in the heap.

*Rearrange String (hard)

767. Reorganize String Design Gurus Educative.io

Problem Statement

Given a string, find if its letters can be rearranged in such a way that no two same characters come next to each other.

Example 1:

1
2
3
Input: "aappp"
Output: "papap"
Explanation: In "papap", none of the repeating characters come next to each other.

Example 2:

1
2
3
Input: "Programming"
Output: "rgmrgmPiano" or "gmringmrPoa" or "gmrPagimnor", etc.
Explanation: None of the repeating characters come next to each other.

Example 3:

1
2
3
Input: "aapa"
Output: ""
Explanation: In all arrangements of "aapa", atleast two 'a' will come together e.g., "apaa", "paaa".

Constraints:

  • 1 <= s.length <= 500
  • s consists of lowercase English letters.

Solution

This problem follows the Top ‘K’ Numbers pattern. We can follow a greedy approach to find an arrangement of the given string where no two same characters come next to each other.

We can work in a stepwise fashion to create a string with all characters from the input string. Following a greedy approach, we should first append the most frequent characters to the output strings, for which we can use a Max Heap. By appending the most frequent character first, we have the best chance to find a string where no two same characters come next to each other.

So in each step, we should append one occurrence of the highest frequency character to the output string. We will not put this character back in the heap to ensure that no two same characters are adjacent to each other. In the next step, we should process the next most frequent character from the heap in the same way and then, at the end of this step, insert the character from the previous step back to the heap after decrementing its frequency.

Following this algorithm, if we can append all the characters from the input string to the output string, we would have successfully found an arrangement of the given string where no two same characters appeared adjacent to each other.

Code

Here is what our algorithm will look like:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
from heapq import *

class Solution:
  def rearrangeString(self, str1):
    charFrequencyMap = {}
    for char in str1:
      charFrequencyMap[char] = charFrequencyMap.get(char, 0) + 1

    maxHeap = []
    # add all characters to the max heap
    for char, frequency in charFrequencyMap.items():
      heappush(maxHeap, (-frequency, char))

    previousChar, previousFrequency = None, 0
    resultString = []
    while maxHeap:
      frequency, char = heappop(maxHeap)
      # add the previous entry back in the heap if its frequency is greater than zero
      if previousChar and -previousFrequency > 0:
        heappush(maxHeap, (previousFrequency, previousChar))
      # append the current character to the result string and decrement its count
      resultString.append(char)
      previousChar = char
      previousFrequency = frequency+1  # decrement the frequency

    # if we were successful in appending all the characters to the result string, return it
    return ''.join(resultString) if len(resultString) == len(str1) else ""


def main():
  sol = Solution()
  print("Rearranged string:  " + sol.rearrangeString("aappp"))
  print("Rearranged string:  " + sol.rearrangeString("Programming"))
  print("Rearranged string:  " + sol.rearrangeString("aapa"))


main()

Time complexity

The time complexity of the above algorithm is O(N\logN)* where ‘N’ is the number of characters in the input string.

Space complexity

The space complexity will be O(N), as in the worst case, we need to store all the ‘N’ characters in the HashMap.

Problem Challenge 1

Leetcode 358 会员 Design Gurus Educative.io

Rearrange String K Distance Apart (hard)

Given a string and a number ‘K’, find if the string can be rearranged such that the same characters are at least ‘K’ distance apart from each other.

Example 1:

1
2
3
Input: "mmpp", K=2
Output: "mpmp" or "pmpm"
Explanation: All same characters are 2 distance apart.

Example 2:

1
2
3
Input: "Programming", K=3
Output: "rgmPrgmiano" or "gmringmrPoa" or "gmrPagimnor" and a few more
Explanation: All same characters are 3 distance apart.

Example 3:

1
2
3
Input: "aab", K=2
Output: "aba"
Explanation: All same characters are 2 distance apart.

Example 4:

1
2
3
Input: "aappa", K=3
Output: ""
Explanation: We cannot find an arrangement of the string where any two 'a' are 3 distance apart.

Constraints:

  • 1 <= str.length <= 3 * 10^5
  • str consists of only lowercase English letters.
  • 0 <= k <= str.length

Solution

This problem follows the Top ‘K’ Numbers pattern and is quite similar to Rearrange String. The only difference is that in the ‘Rearrange String’ the same characters need not be adjacent i.e., they should be at least ‘2’ distance apart (in other words, there should be at least one character between two same characters), while in the current problem, the same characters should be ‘K’ distance apart.

Following a similar approach, since we were inserting a character back in the heap in the next iteration, in this problem, we will re-insert the character after ‘K’ iterations. We can keep track of previous characters in a queue to insert them back in the heap after ‘K’ iterations.

Code

Here is what our algorithm will look like:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
from heapq import *
from collections import deque

class Solution:
  def reorganizeString(self, str, k):
    if k <= 1: 
      return str

    charFrequencyMap = {}
    for char in str:
      charFrequencyMap[char] = charFrequencyMap.get(char, 0) + 1

    maxHeap = []
    # add all characters to the max heap
    for char, frequency in charFrequencyMap.items():
      heappush(maxHeap, (-frequency, char))

    queue = deque()
    resultString = []
    while maxHeap:
      frequency, char = heappop(maxHeap)
      # append the current character to the result string and decrement its count
      resultString.append(char)
      # decrement the frequency and append to the queue
      queue.append((char, frequency+1))
      if len(queue) == k:
        char, frequency = queue.popleft()
        if -frequency > 0:
          heappush(maxHeap, (frequency, char))

    # if we were successful in appending all the characters to the result string, return it
    return ''.join(resultString) if len(resultString) == len(str) else ""


def main():
  sol = Solution()
  print("Reorganized string: " + sol.reorganizeString("Programming", 3))
  print("Reorganized string: " + sol.reorganizeString("mmpp", 2))
  print("Reorganized string: " + sol.reorganizeString("aab", 2))
  print("Reorganized string: " + sol.reorganizeString("aapa", 3))


main()

Time complexity

The time complexity of the above algorithm is O(N\logN)* where ‘N’ is the number of characters in the input string.

Space complexity

The space complexity will be O(N), as in the worst case, we need to store all the ‘N’ characters in the HashMap.

#Problem Challenge 2

621. Task Scheduler Design Gurus Educative.io

Scheduling Tasks (hard)

You are given a list of tasks that need to be run, in any order, on a server. Each task will take one CPU interval to execute but once a task has finished, it has a cooling period during which it can’t be run again. If the cooling period for all tasks is ‘K’ intervals, find the minimum number of CPU intervals that the server needs to finish all tasks.

If at any time the server can’t execute any task then it must stay idle.

Example 1:

1
2
3
Input: [a, a, a, b, c, c], K=2
Output: 7
Explanation: a -> c -> b -> a -> c -> idle -> a

Example 2:

1
2
3
Input: [a, b, a], K=3
Output: 5
Explanation: a -> b -> idle -> idle -> a

Constraints:

  • 1 <= tasks.length <= 10^4
  • tasks[i] is an uppercase English letter.
  • 0 <= k <= 100

Solution

This problem follows the Top 'K' Numbers pattern and is quite similar to Rearrange String K Distance Apart. We need to rearrange tasks such that same tasks are ‘K’ distance apart.

Following a similar approach, we will use a Max Heap to execute the highest frequency task first. After executing a task we decrease its frequency and put it in a waiting list. In each iteration, we will try to execute as many as k+1 tasks. For the next iteration, we will put all the waiting tasks back in the Max Heap. If, for any iteration, we are not able to execute k+1 tasks, the CPU has to remain idle for the remaining time in the next iteration.

Code

Here is what our algorithm will look like:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
from heapq import *

class Solution:
  def scheduleTasks(self, tasks, k):
    intervalCount = 0
    taskFrequencyMap = {}
    for char in tasks:
      taskFrequencyMap[char] = taskFrequencyMap.get(char, 0) + 1

    maxHeap = []
    # add all tasks to the max heap
    for char, frequency in taskFrequencyMap.items():
      heappush(maxHeap, (-frequency, char))

    while maxHeap:
      waitList = []
      n = k + 1  # try to execute as many as 'k+1' tasks from the max-heap
      while n > 0 and maxHeap:
        intervalCount += 1
        frequency, char = heappop(maxHeap)
        if -frequency > 1:
          # decrement the frequency and add to the waitList
          waitList.append((frequency+1, char))
        n -= 1

      # put all the waiting list back on the heap
      for frequency, char in waitList:
        heappush(maxHeap, (frequency, char))

      if maxHeap:
        intervalCount += n  # we'll be having 'n' idle intervals for the next iteration

    return intervalCount


def main():
  sol = Solution()
  print("Minimum intervals needed to execute all tasks: " +
        str(sol.scheduleTasks(['a', 'a', 'a', 'b', 'c', 'c'], 2)))
  print("Minimum intervals needed to execute all tasks: " +
        str(sol.scheduleTasks(['a', 'b', 'a'], 3)))


main()

Time complexity

The time complexity of the above algorithm is O(N\logN)* where ‘N’ is the number of tasks. Our while loop will iterate once for each occurrence of the task in the input (i.e. ‘N’) and in each iteration we will remove a task from the heap which will take O(logN) time. Hence the overall time complexity of our algorithm is O(N\logN)*.

Space complexity

The space complexity will be O(N), as in the worst case, we need to store all the ‘N’ tasks in the HashMap.

Problem Challenge 3

895. Maximum Frequency Stack Design Gurus Educative.io

Frequency Stack (hard)

Design a class that simulates a Stack data structure, implementing the following two operations:

  1. push(int num): Pushes the number ‘num’ on the stack.
  2. pop(): Returns the most frequent number in the stack. If there is a tie, return the number which was pushed later.

Example:

1
2
3
4
5
After following push operations: push(1), push(2), push(3), push(2), push(1), push(2), push(5)
 
1. pop() should return 2, as it is the most frequent number
2. Next pop() should return 1
3. Next pop() should return 2

Constraints:

  • 0 <= val <= 10^9
  • At most 2 * 10^4 calls will be made to push and pop.
  • It is guaranteed that there will be at least one element in the stack before calling pop.

Solution

This problem follows the Top ‘K’ Elements pattern, and shares similarities with Top ‘K’ Frequent Numbers.

We can use a Max Heap to store the numbers. Instead of comparing the numbers we will compare their frequencies so that the root of the heap is always the most frequently occurring number. There are two issues that need to be resolved though:

  1. How can we keep track of the frequencies of numbers in the heap? When we are pushing a new number to the Max Heap, we don’t know how many times the number has already appeared in the Max Heap. To resolve this, we will maintain a HashMap to store the current frequency of each number. Thus whenever we push a new number in the heap, we will increment its frequency in the HashMap and when we pop, we will decrement its frequency.
  2. If two numbers have the same frequency, we will need to return the number which was pushed later while popping. To resolve this, we need to attach a sequence number to every number to know which number came first.

In short, we will keep three things with every number that we push to the heap:

1
2
3
1. number // value of the number
2. frequency // current frequency of the number when it was pushed to the heap
3. sequenceNumber // a sequence number, to know what number came first

Code

Here is what our algorithm will look like:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
# 需要注意的是，在pop之后，已经在heap中的三元组中的frequency_map[num]的值还是旧的，但是没有问题，因为在栈中的顺序不会改变

from heapq import *


class Element:

    def __init__(self, number, frequency, sequenceNumber):
        self.number = number
        self.frequency = frequency
        self.sequenceNumber = sequenceNumber

    def __lt__(self, other):
        # higher frequency wins
        if self.frequency != other.frequency:
            return self.frequency > other.frequency
        # if both elements have same frequency, return the element that was pushed later
        return self.sequenceNumber > other.sequenceNumber


class Solution:

    def __init__(self):
        self.sequenceNumber = 0
        self.maxHeap = []
        self.frequencyMap = {}

    def push(self, num):
        self.frequencyMap[num] = self.frequencyMap.get(num, 0) + 1
        heappush(self.maxHeap, Element(
            num, self.frequencyMap[num], self.sequenceNumber))
        self.sequenceNumber += 1

    def pop(self):
        num = heappop(self.maxHeap).number
        # decrement the frequency or remove if this is the last number
        if self.frequencyMap[num] > 1:
            self.frequencyMap[num] -= 1
        else:
            del self.frequencyMap[num]

        return num


def main():
    sol = Solution()
    sol.push(1)
    sol.push(2)
    sol.push(3)
    sol.push(2)
    sol.push(1)
    sol.push(2)
    sol.push(5)
    print(sol.pop())
    print(sol.pop())
    print(sol.pop())


main()



#=======================leetcode=========================
from heapq import *


class FrequencyStack:
    def __init__(self):
        self.sequence_number = 0
        self.max_heap = []
        self.frequency_map = {}

    def push(self, num):
        self.frequency_map[num] = self.frequency_map.get(num, 0) + 1
        heappush(self.max_heap, (-self.frequency_map[num], -self.sequence_number, num))
        self.sequence_number += 1

    def pop(self):
        num = heappop(self.max_heap)[2]
        if self.frequency_map[num] > 1:
            self.frequency_map[num] -= 1
        else:
            del self.frequency_map[num]
        return num


def main():
    stack = FrequencyStack()
    stack.push(1)
    stack.push(2)
    stack.push(3)
    stack.push(2)
    stack.push(1)
    stack.push(2)
    stack.push(5)
    print(stack.pop())
    print(stack.pop())
    print(stack.pop())
    print(stack.pop())
    print(stack.pop())
    print(stack.pop())
    print(stack.pop())


if __name__ == '__main__':
    main()

Author：Hasuer

Link：https://hasuer.github.io/18-pattern-top-k-elements/index.html

Publish date：May 18th 2024, 4:53:51 pm

Update date：May 28th 2024, 11:29:44 am

License：本文采用知识共享署名-非商业性使用 4.0 国际许可协议进行许可

CATALOG
  1. 1. Introduction
  2. 2. Top ‘K’ Numbers (easy)
    1. 2.1. Problem Statement
    2. 2.2. Solution
      1. 2.2.1. Time complexity
      2. 2.2.2. Space complexity
  3. 3. Kth Smallest Number (easy)
    1. 3.1. Problem Statement
    2. 3.2. Solution
    3. 3.3. Code
      1. 3.3.1. Time complexity
      2. 3.3.2. Space complexity
    4. 3.4. An Alternate Approach
  4. 4. ‘K’ Closest Points to the Origin (easy)
    1. 4.1. Problem Statement
    2. 4.2. Solution
    3. 4.3. Code
      1. 4.3.1. Time complexity
      2. 4.3.2. Space complexity
  5. 5. Connect Ropes (easy)
    1. 5.1. Problem Statement
    2. 5.2. Solution
    3. 5.3. Code
      1. 5.3.1. Time complexity
      2. 5.3.2. Space complexity
  6. 6. Top ‘K’ Frequent Numbers (medium)
    1. 6.1. Problem Statement
    2. 6.2. Solution
    3. 6.3. Code
      1. 6.3.1. Time complexity
      2. 6.3.2. Space complexity
  7. 7. Frequency Sort (medium)
    1. 7.1. Problem Statement
    2. 7.2. Solution
    3. 7.3. Code
      1. 7.3.1. Time complexity
      2. 7.3.2. Space complexity
  8. 8. Kth Largest Number in a Stream (medium)
    1. 8.1. Problem Statement
    2. 8.2. Solution
    3. 8.3. Code
      1. 8.3.1. Time complexity
      2. 8.3.2. Space complexity
  9. 9. ‘K’ Closest Numbers (medium)
    1. 9.1. Problem Statement
    2. 9.2. Solution
    3. 9.3. Code
      1. 9.3.1. Time complexity
      2. 9.3.2. Space complexity
    4. 9.4. Alternate Solution using Two Pointers
      1. 9.4.1. Time complexity
      2. 9.4.2. Space complexity
  10. 10. Maximum Distinct Elements (medium)
    1. 10.1. Problem Statement
    2. 10.2. Solution
    3. 10.3. Code
      1. 10.3.1. Time complexity
      2. 10.3.2. Space complexity
  11. 11. Sum of Elements (medium)
    1. 11.1. Problem Statement
    2. 11.2. Solution
    3. 11.3. Code
      1. 11.3.1. Time complexity
      2. 11.3.2. Space complexity
    4. 11.4. Alternate Solution
      1. 11.4.1. Time complexity
      2. 11.4.2. Space complexity
  12. 12. *Rearrange String (hard)
    1. 12.1. Problem Statement
    2. 12.2. Solution
    3. 12.3. Code
      1. 12.3.1. Time complexity
      2. 12.3.2. Space complexity
  13. 13. Problem Challenge 1
    1. 13.1. Rearrange String K Distance Apart (hard)
    2. 13.2. Solution
    3. 13.3. Code
      1. 13.3.1. Time complexity
      2. 13.3.2. Space complexity
  14. 14. #Problem Challenge 2
    1. 14.1. Scheduling Tasks (hard)
    2. 14.2. Solution
    3. 14.3. Code
      1. 14.3.1. Time complexity
      2. 14.3.2. Space complexity
  15. 15. Problem Challenge 3
    1. 15.1. Frequency Stack (hard)
    2. 15.2. Solution
    3. 15.3. Code
Total : 41
2024
2022
2021
Interview
技术笔记 Grokking-Interview-Pattern