Hasuer's Studio.

10. Pattern Tree Breadth First Search

Grokking Interview Pattern Interview
Word count: 4.3kReading time: 26 min
2024/05/10

Introduction

This pattern is based on the Breadth First Search (BFS) technique to traverse a tree.

Any problem involving the traversal of a tree in a level-by-level order can be efficiently solved using this approach. We will use a Queue to keep track of all the nodes of a level before we jump onto the next level. This also means that the space complexity of the algorithm will be O(W), where ‘W’ is the maximum number of nodes on any level.

Let’s jump onto our first problem to understand this pattern.

Binary Tree Level Order Traversal (easy)

Top Interview 150 | 102. Binary Tree Level Order Traversal Design Gurus Educative.io

Problem Statement

Given a binary tree, populate an array to represent its level-by-level traversal. You should populate the values of all nodes of each level from left to right in separate sub-arrays.

Example 1:

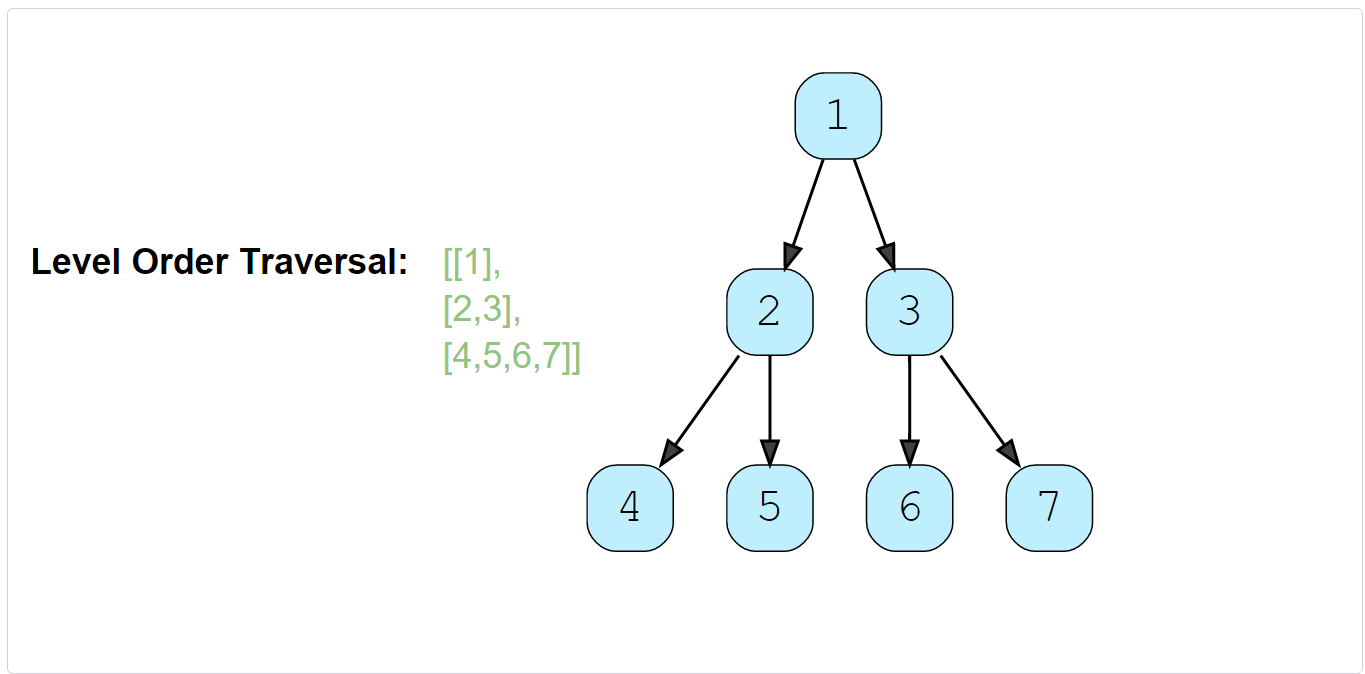
Example 2:

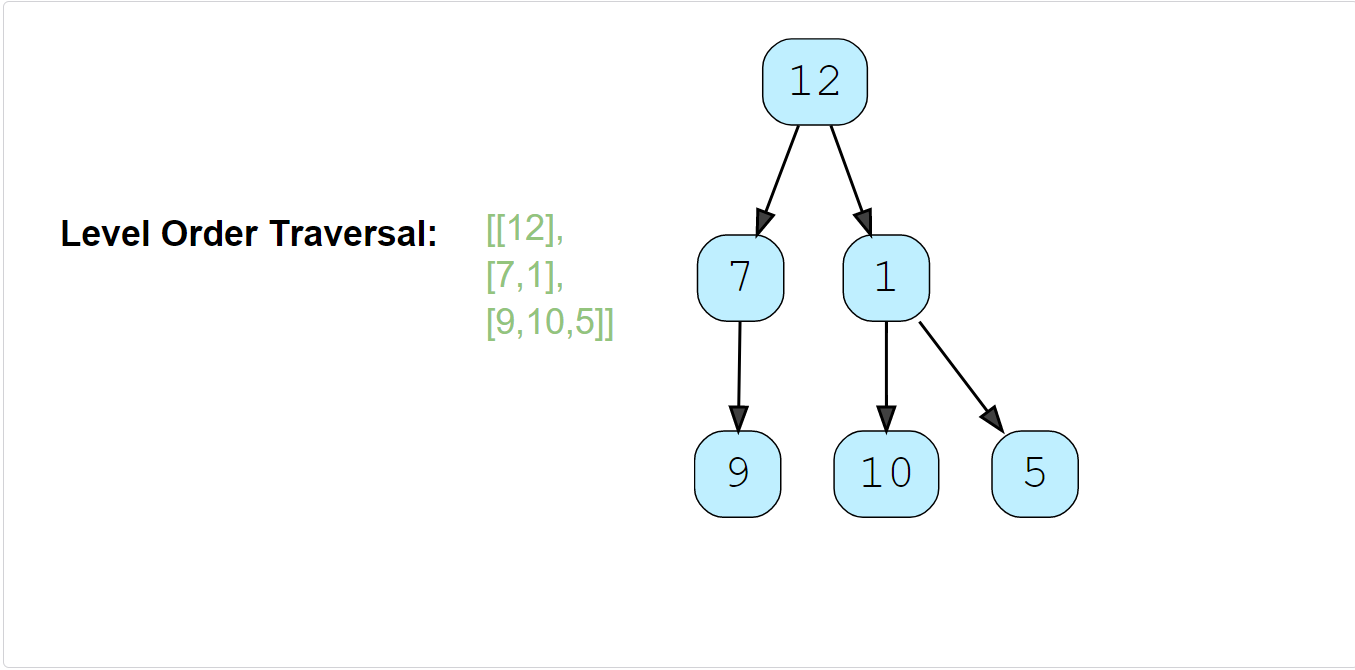
Constraints:

  • The number of nodes in the tree is in the range [0, 2000].
  • -1000 <= Node.val <= 1000

Solution

Since we need to traverse all nodes of each level before moving onto the next level, we can use the Breadth First Search (BFS) technique to solve this problem.

We can use a Queue to efficiently traverse in BFS fashion. Here are the steps of our algorithm:

  1. Start by pushing the root node to the queue.
  2. Keep iterating until the queue is empty.
  3. In each iteration, first count the elements in the queue (let’s call it levelSize). We will have these many nodes in the current level.
  4. Next, remove levelSize nodes from the queue and push their value in an array to represent the current level.
  5. After removing each node from the queue, insert both of its children into the queue.
  6. If the queue is not empty, repeat from step 3 for the next level.

Let’s take the example-2 mentioned above to visually represent our algorithm:

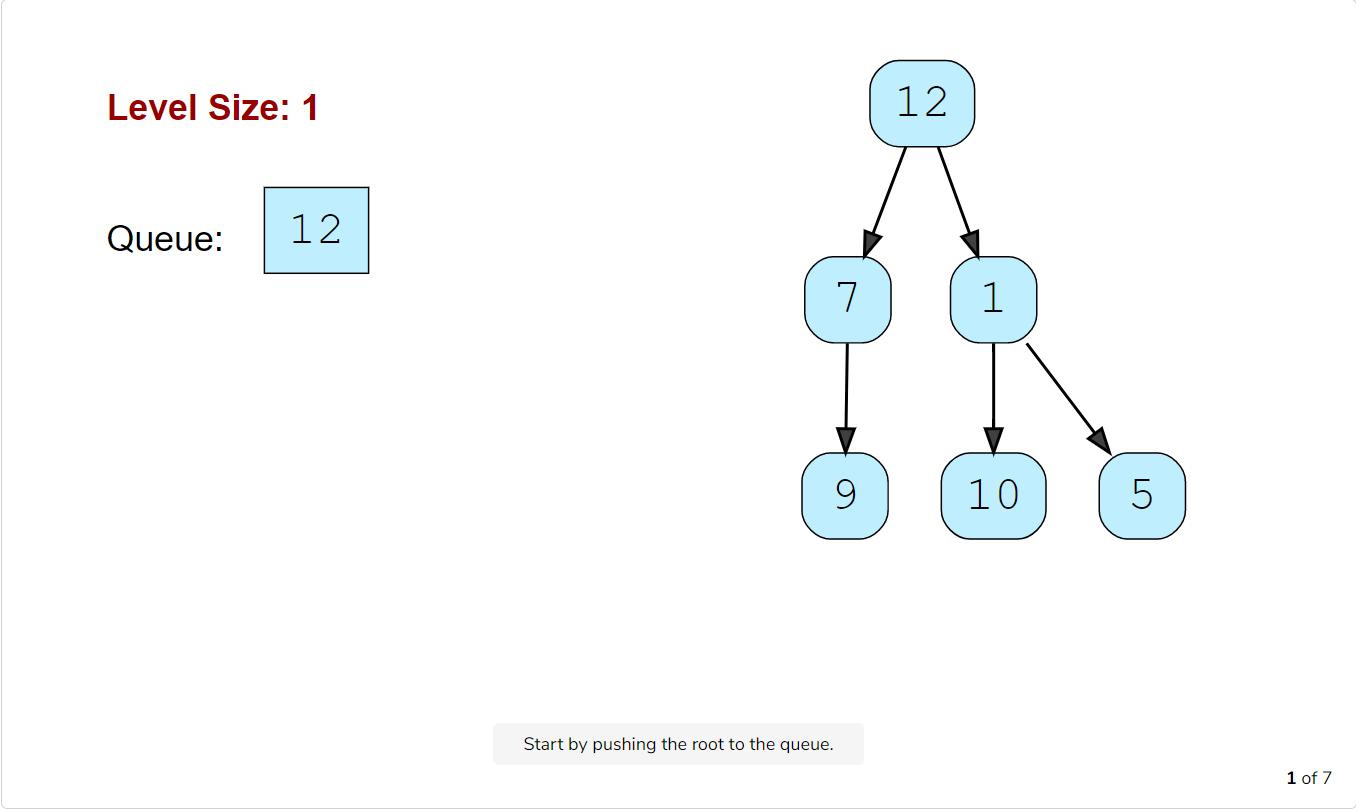
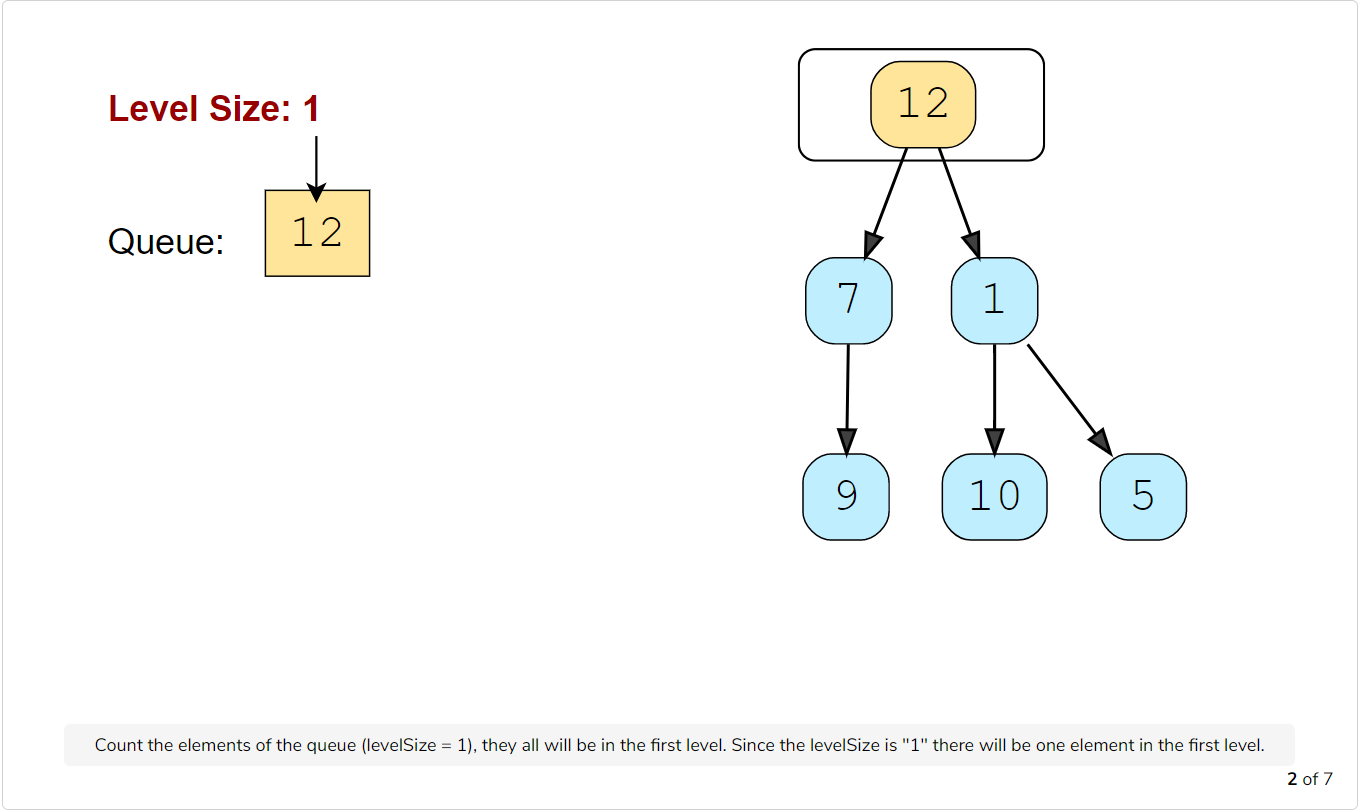
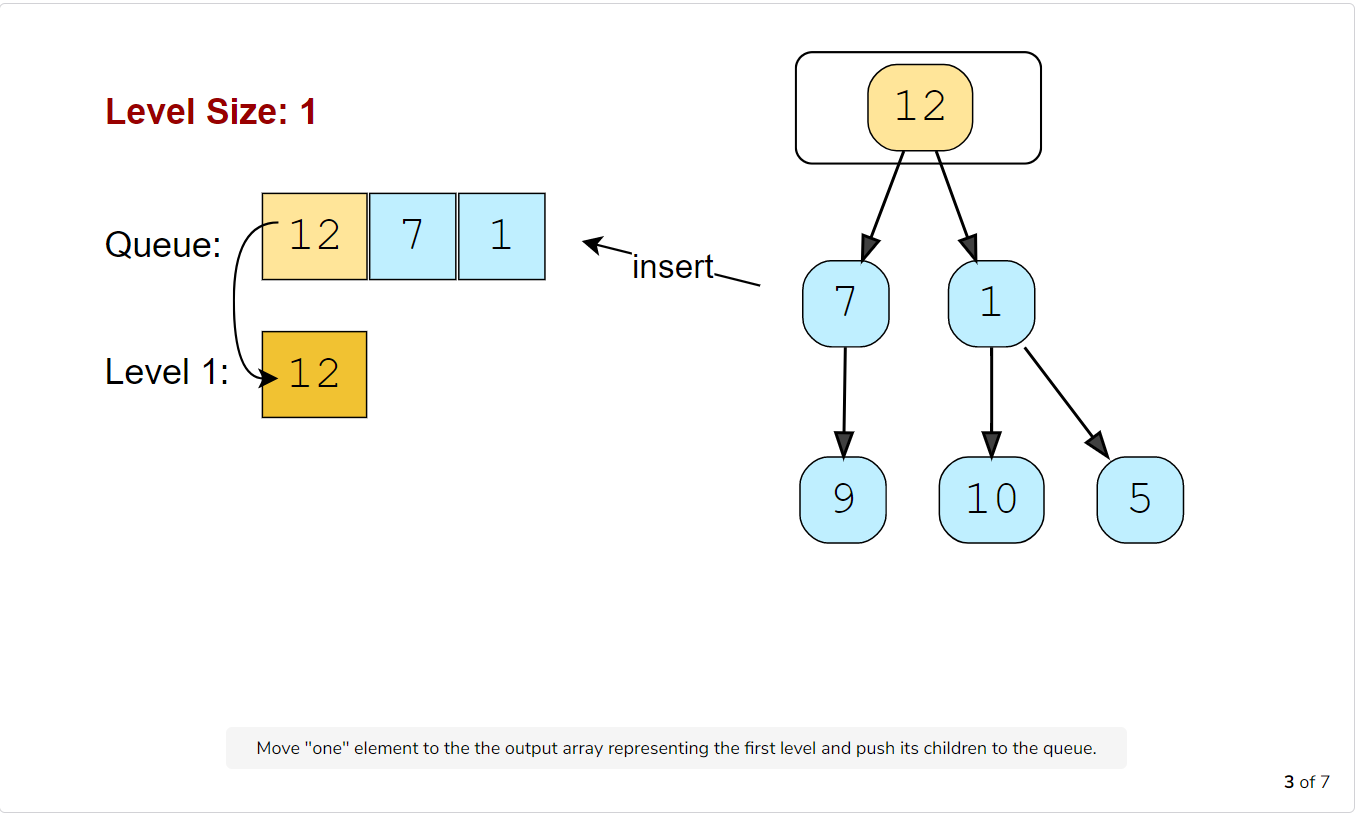
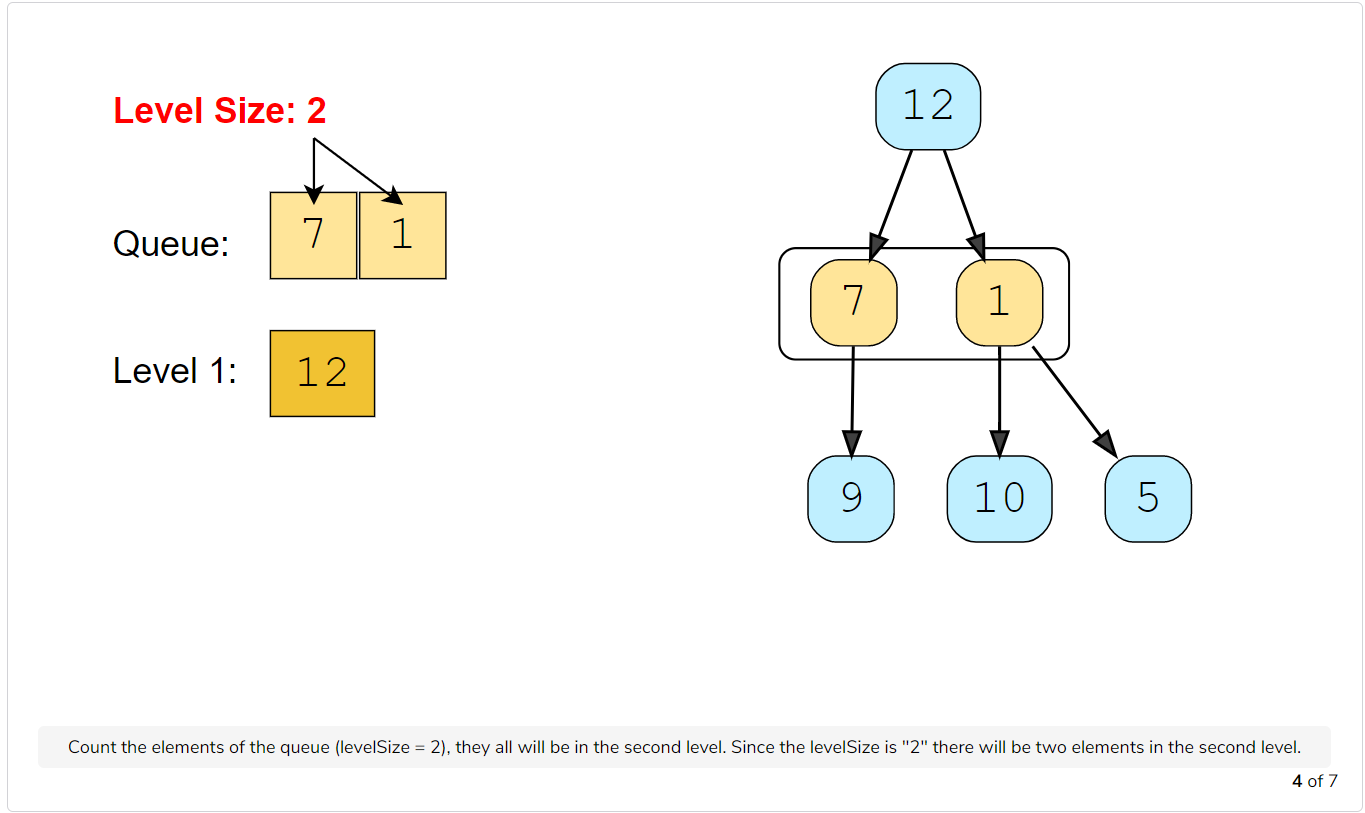
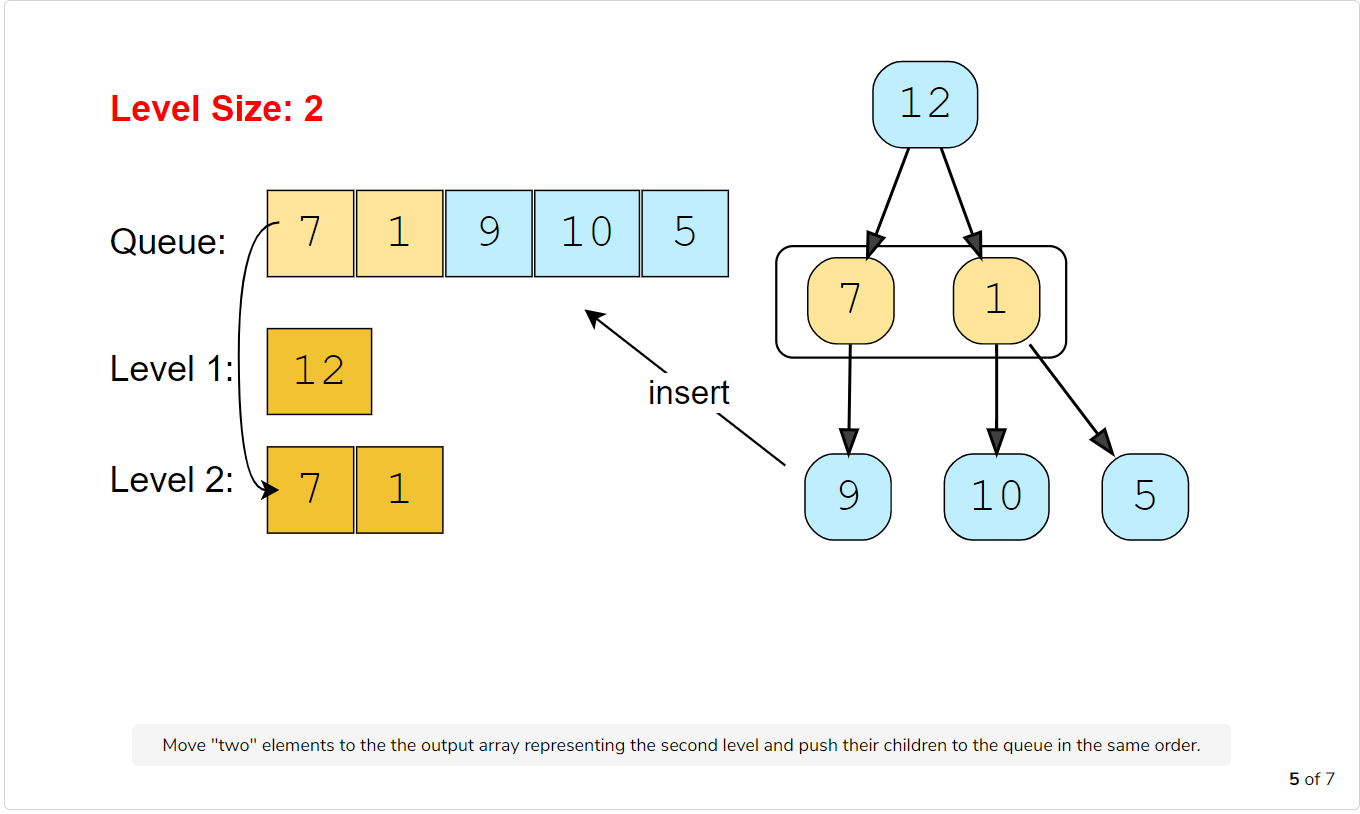
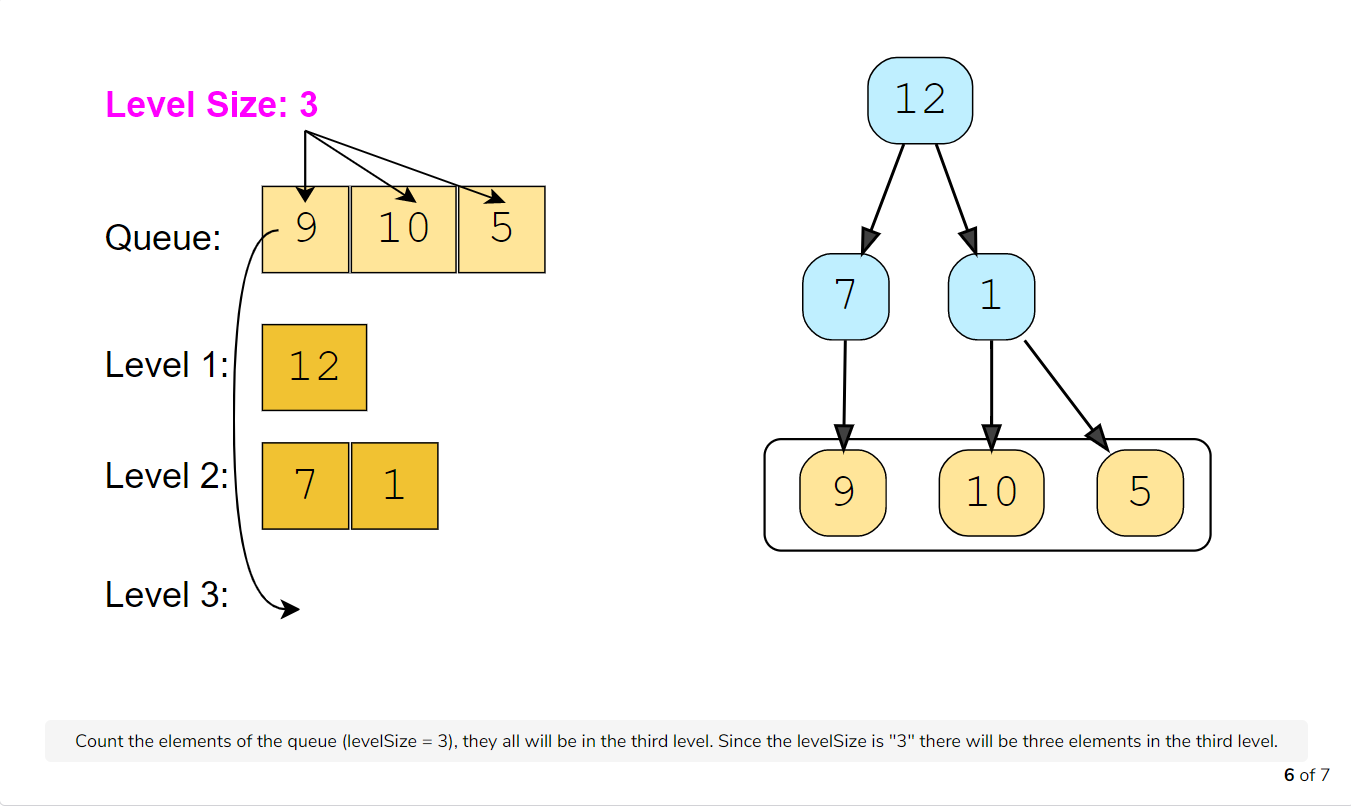
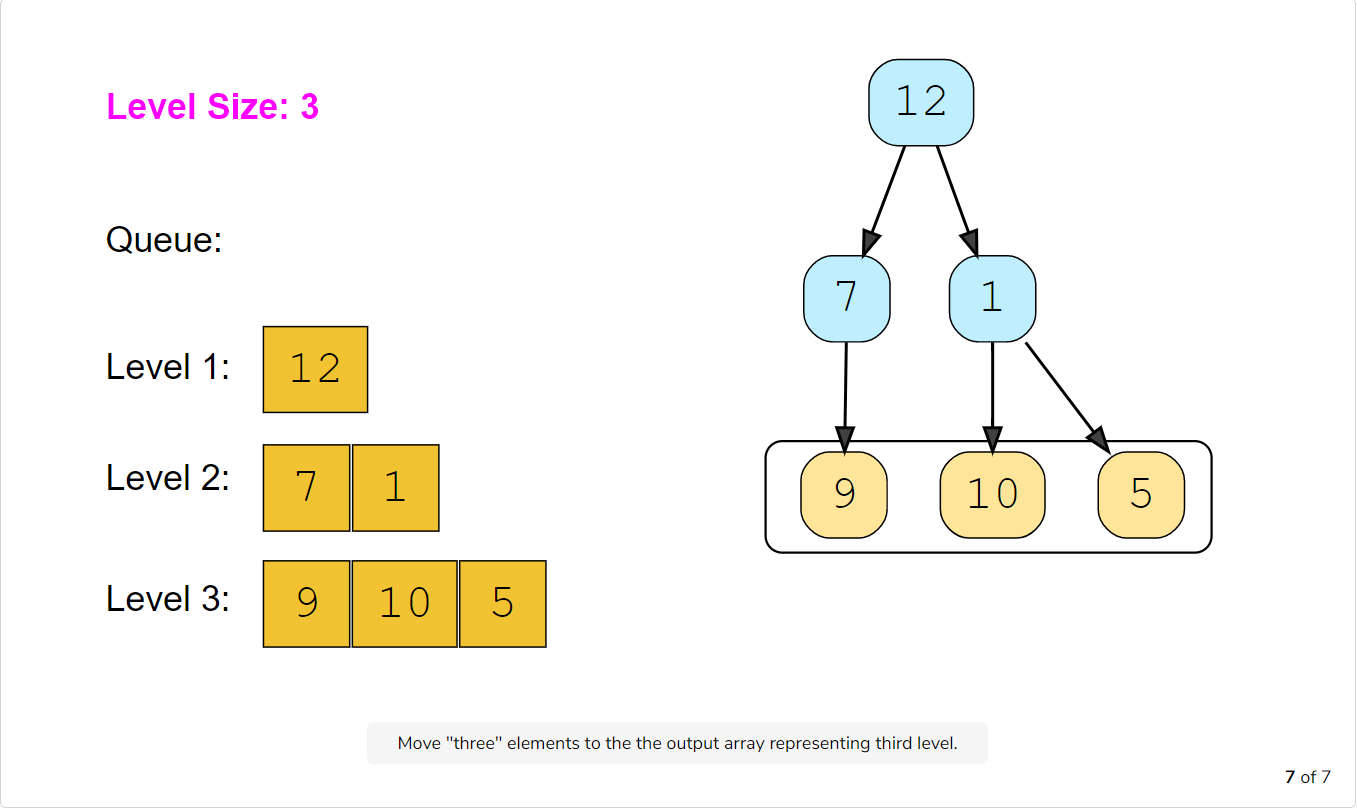
Code

Here is what our algorithm will look like:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
from collections import deque


# class TreeNode:
#   def __init__(self, val):
#     self.val = val
#     self.left, self.right = None, None


class Solution:
    def traverse(self, root):
        result = []
        if root is None:
            return result

        queue = deque()
        queue.append(root)
        while queue:
            levelSize = len(queue)
            currentLevel = []
            for _ in range(levelSize):
                currentNode = queue.popleft()
                # add the node to the current level
                currentLevel.append(currentNode.val)
                # insert the children of current node in the queue
                if currentNode.left:
                    queue.append(currentNode.left)
                if currentNode.right:
                    queue.append(currentNode.right)

            result.append(currentLevel)

        return result


def main():
    sol = Solution()
    root = TreeNode(12)
    root.left = TreeNode(7)
    root.right = TreeNode(1)
    root.left.left = TreeNode(9)
    root.right.left = TreeNode(10)
    root.right.right = TreeNode(5)
    print("Level order traversal: " + str(sol.traverse(root)))


main()

Time complexity

The time complexity of the above algorithm is O(N), where ‘N’ is the total number of nodes in the tree. This is due to the fact that we traverse each node once.

Space complexity

The space complexity of the above algorithm will be O(N) as we need to return a list containing the level order traversal. We will also need O(N) space for the queue. Since we can have a maximum of N/2 nodes at any level (this could happen only at the lowest level), therefore we will need O(N) space to store them in the queue.

Reverse Level Order Traversal (easy)

107. Binary Tree Level Order Traversal II Design Gurus Educative.io

Problem Statement

Given a binary tree, populate an array to represent its level-by-level traversal in reverse order, i.e., the lowest level comes first. You should populate the values of all nodes in each level from left to right in separate sub-arrays.

Example 1:

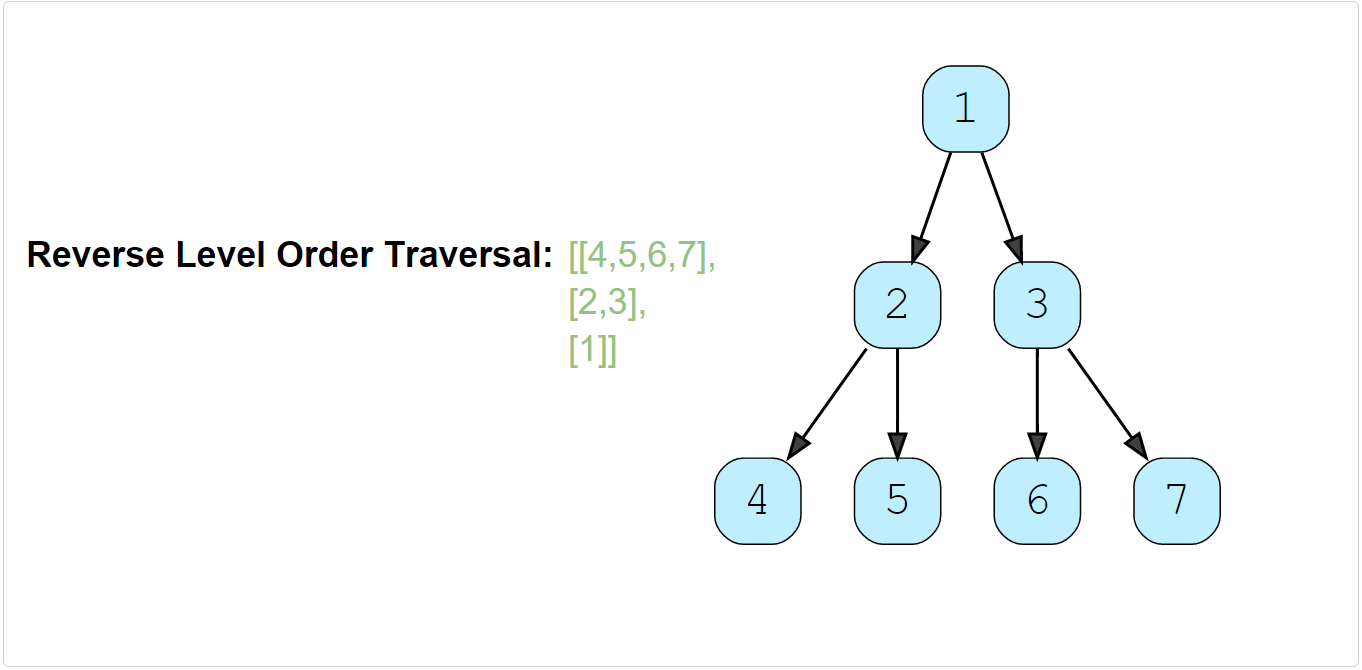
Example 2:

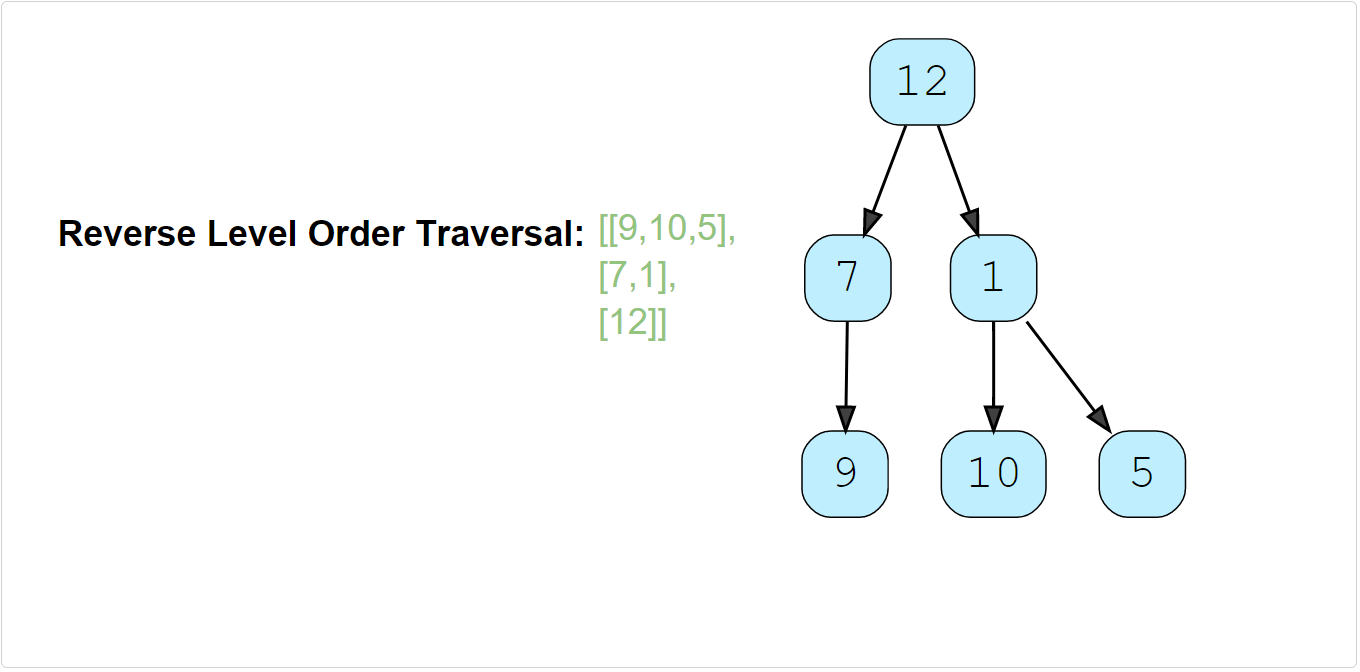
Constraints:

  • The number of nodes in the tree is in the range [0, 2000].
  • -1000 <= Node.val <= 1000

Solution

This problem follows the Binary Tree Level Order Traversal pattern. We can follow the same BFS approach. The only difference will be that instead of appending the current level at the end, we will append the current level at the beginning of the result list.

Here is the visual representation of the algorithm:

Code

Here is what our algorithm will look like; only the highlighted lines have changed. Please note that, for Java, we will use a LinkedList instead of an ArrayList for our result list. As in the case of ArrayList, appending an element at the beginning means shifting all the existing elements. Since we need to append the level array at the beginning of the result list, a LinkedList will be better, as this shifting of elements is not required in a LinkedList. Similarly, we will use a double-ended queue (deque) for Python, C++, and JavaScript.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
from collections import deque


# class TreeNode:
#   def __init__(self, val):
#     self.val = val
#     self.left, self.right = None, None


class Solution:
    def traverse(self, root):
        result = deque()
        if root is None:
            return result

        queue = deque()
        queue.append(root)
        while queue:
            levelSize = len(queue)
            currentLevel = []
            for _ in range(levelSize):
                currentNode = queue.popleft()
                # add the node to the current level
                currentLevel.append(currentNode.val)
                # insert the children of current node in the queue
                if currentNode.left:
                    queue.append(currentNode.left)
                if currentNode.right:
                    queue.append(currentNode.right)

            result.appendleft(currentLevel)

        result = [list(sublist) for sublist in result]
        return result


def main():
    sol = Solution()
    root = TreeNode(12)
    root.left = TreeNode(7)
    root.right = TreeNode(1)
    root.left.left = TreeNode(9)
    root.right.left = TreeNode(10)
    root.right.right = TreeNode(5)
    print("Reverse level order traversal: " + str(sol.traverse(root)))


main()

Time complexity

The time complexity of the above algorithm is O(N), where ‘N’ is the total number of nodes in the tree. This is due to the fact that we traverse each node once.

Space complexity

The space complexity of the above algorithm will be O(N) as we need to return a list containing the level order traversal. We will also need O(N) space for the queue. Since we can have a maximum of N/2 nodes at any level (this could happen only at the lowest level), therefore we will need O(N) space to store them in the queue.

Zigzag Traversal (medium)

Top Interview 150 | 103. Binary Tree Zigzag Level Order Traversal Design Gurus Educative.io

Problem Statement

Given a binary tree, populate an array to represent its zigzag level order traversal. You should populate the values of all nodes of the first level from left to right, then right to left for the next level and keep alternating in the same manner for the following levels.

Example 1:

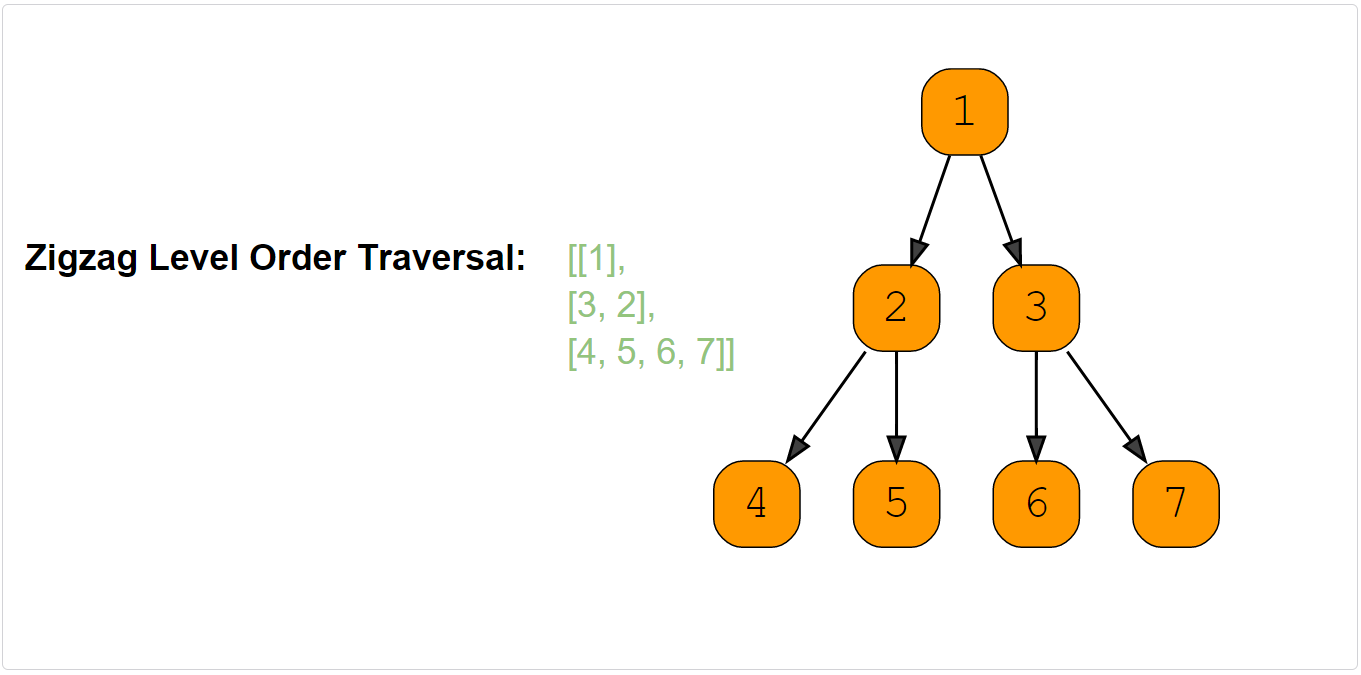
Example 2:

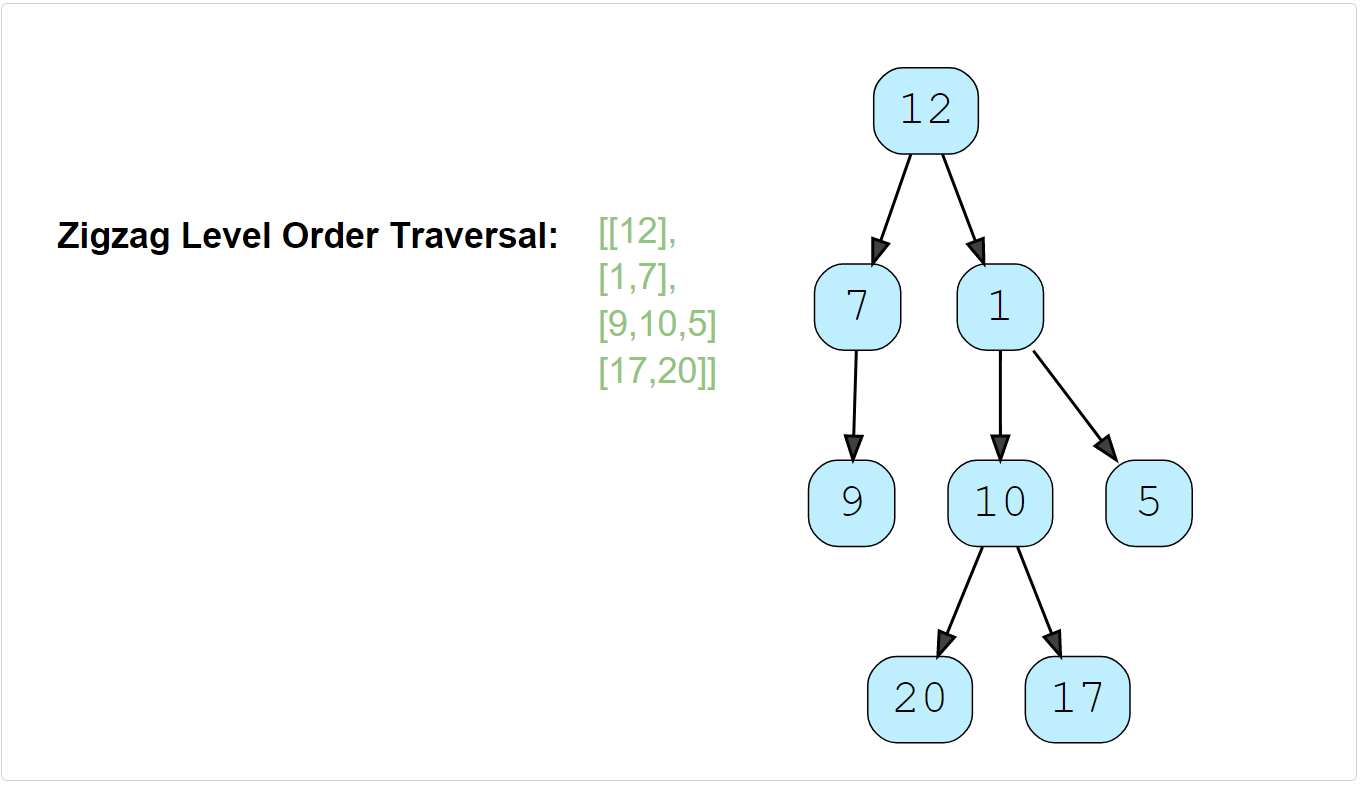
Constraints:

  • The number of nodes in the tree is in the range [0, 2000].
  • -1000 <= Node.val <= 1000

Solution

This problem follows the Binary Tree Level Order Traversal pattern. We can follow the same BFS approach. The only additional step we have to keep in mind is to alternate the level order traversal, which means that for every other level, we will traverse similar to Reverse Level Order Traversal.

Here is the visual representation of the algorithm:

Code

Here is what our algorithm will look like, only the highlighted lines have changed:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
from collections import deque


# class TreeNode:
#   def __init__(self, val):
#     self.val = val
#     self.left, self.right = None, None


class Solution:
    def traverse(self, root):
        result = []
        if root is None:
            return result

        queue = deque()
        queue.append(root)
        leftToRight = True
        while queue:
            levelSize = len(queue)
            currentLevel = deque()
            for _ in range(levelSize):
                currentNode = queue.popleft()

                # add the node to the current level based on the traverse direction
                if leftToRight:
                    currentLevel.append(currentNode.val)
                else:
                    currentLevel.appendleft(currentNode.val)

                # insert the children of current node in the queue
                if currentNode.left:
                    queue.append(currentNode.left)
                if currentNode.right:
                    queue.append(currentNode.right)

            result.append(list(currentLevel))
            # reverse the traversal direction
            leftToRight = not leftToRight

        return result


def main():
    sol = Solution()
    root = TreeNode(12)
    root.left = TreeNode(7)
    root.right = TreeNode(1)
    root.left.left = TreeNode(9)
    root.right.left = TreeNode(10)
    root.right.right = TreeNode(5)
    root.right.left.left = TreeNode(20)
    root.right.left.right = TreeNode(17)
    print("Zigzag traversal: " + str(sol.traverse(root)))


main()

Time complexity

The time complexity of the above algorithm is O(N), where ‘N’ is the total number of nodes in the tree. This is due to the fact that we traverse each node once.

Space complexity

The space complexity of the above algorithm will be O(N) as we need to return a list containing the level order traversal. We will also need O(N) space for the queue. Since we can have a maximum of N/2 nodes at any level (this could happen only at the lowest level), therefore we will need O(N) space to store them in the queue.

Level Averages in a Binary Tree (easy)

Top Interview 150 | 637. Average of Levels in Binary Tree Design Gurus Educative.io

Problem Statement

Given a binary tree, populate an array to represent the averages of all of its levels.

Example 1:

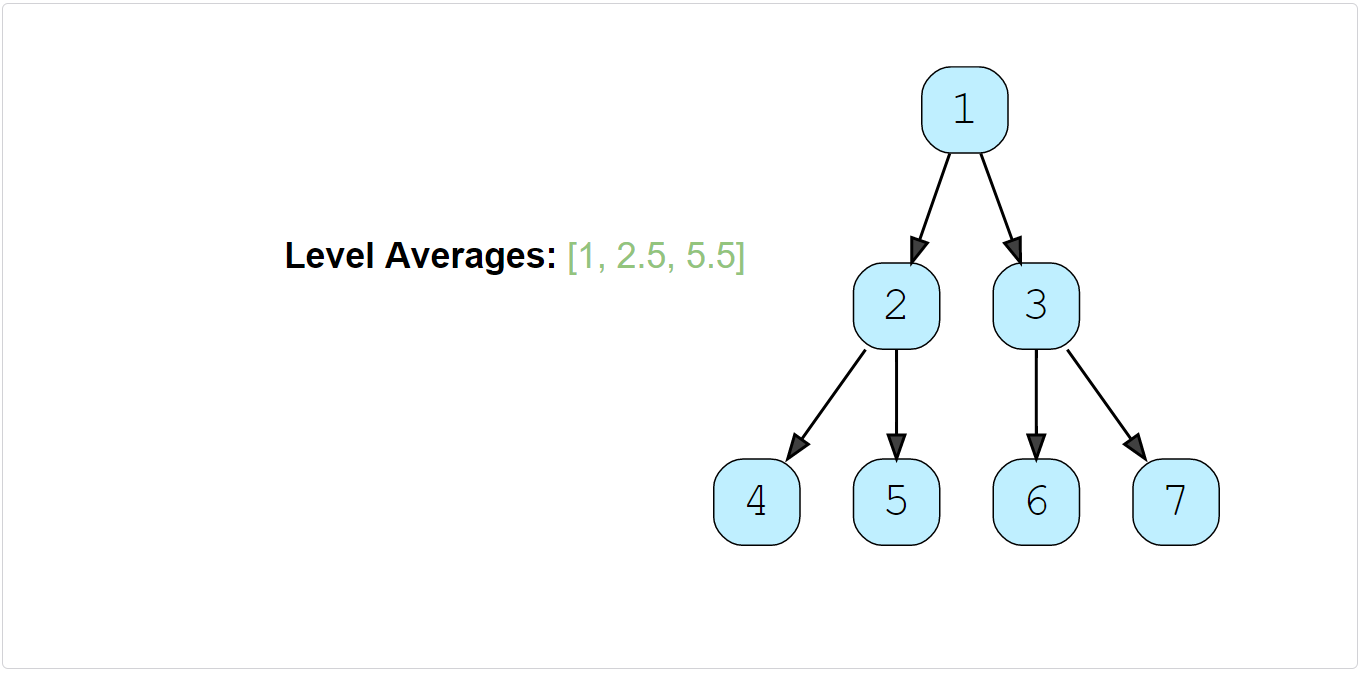
Example 2:

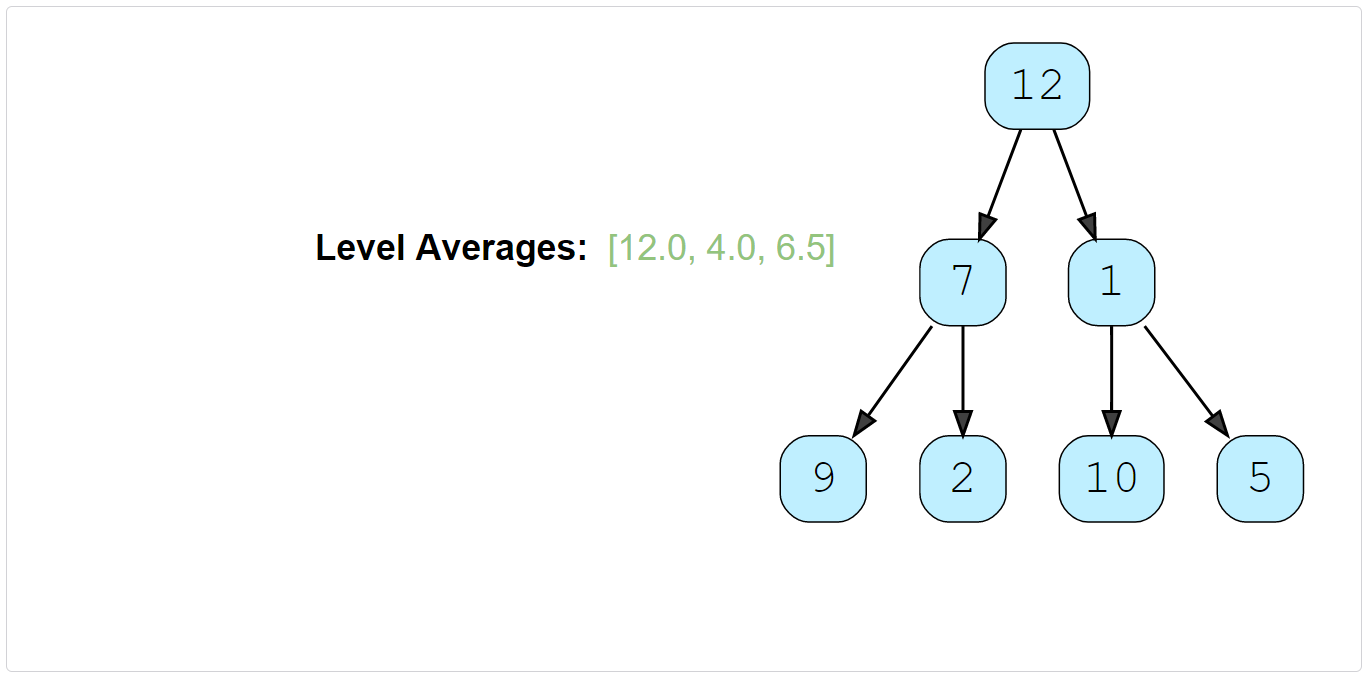
Constraints:

  • The number of nodes in the tree is in the range [1, 10^4].
  • -2^31 <= Node.val <= 2^31 - 1

Solution

This problem follows the Binary Tree Level Order Traversal pattern. We can follow the same BFS approach. The only difference will be that instead of keeping track of all nodes of a level, we will only track the running sum of the values of all nodes in each level. In the end, we will append the average of the current level to the result array.

Here is the visual representation of the algorithm:

Code

Here is what our algorithm will look like; only the highlighted lines have changed:67u

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
from collections import deque


# class TreeNode:
#   def __init__(self, val):
#     self.val = val
#     self.left, self.right = None, None

class Solution:
    def findLevelAverages(self, root):
        result = []
        if root is None:
            return result

        queue = deque()
        queue.append(root)
        while queue:
            levelSize = len(queue)
            levelSum = 0.0
            for _ in range(levelSize):
                currentNode = queue.popleft()
                # add the node's value to the running sum
                levelSum += currentNode.val
                # insert the children of current node to the queue
                if currentNode.left:
                    queue.append(currentNode.left)
                if currentNode.right:
                    queue.append(currentNode.right)

            # append the current level's average to the result array
            result.append(levelSum / levelSize)

        return result


def main():
    sol = Solution()
    root = TreeNode(12)
    root.left = TreeNode(7)
    root.right = TreeNode(1)
    root.left.left = TreeNode(9)
    root.left.right = TreeNode(2)
    root.right.left = TreeNode(10)
    root.right.right = TreeNode(5)
    print("Level averages are: " + str(sol.findLevelAverages(root)))


main()

Time complexity

The time complexity of the above algorithm is O(N), where ‘N’ is the total number of nodes in the tree. This is due to the fact that we traverse each node once.

Space complexity

The space complexity of the above algorithm will be O(N) which is required for the queue. Since we can have a maximum of N/2 nodes at any level (this could happen only at the lowest level), therefore we will need O(N) space to store them in the queue.

Similar Problems

Problem 1: Find the largest value on each level of a binary tree.

Solution: We will follow a similar approach, but instead of having a running sum we will track the maximum value of each level.

1
maxValue = max(maxValue, currentNode.val)

# Minimum Depth of a Binary Tree (easy)

111. Minimum Depth of Binary Tree Design Gurus Educative.io

Problem Statement

Find the minimum depth of a binary tree. The minimum depth is the number of nodes along the shortest path from the root node to the nearest leaf node.

Example 1:

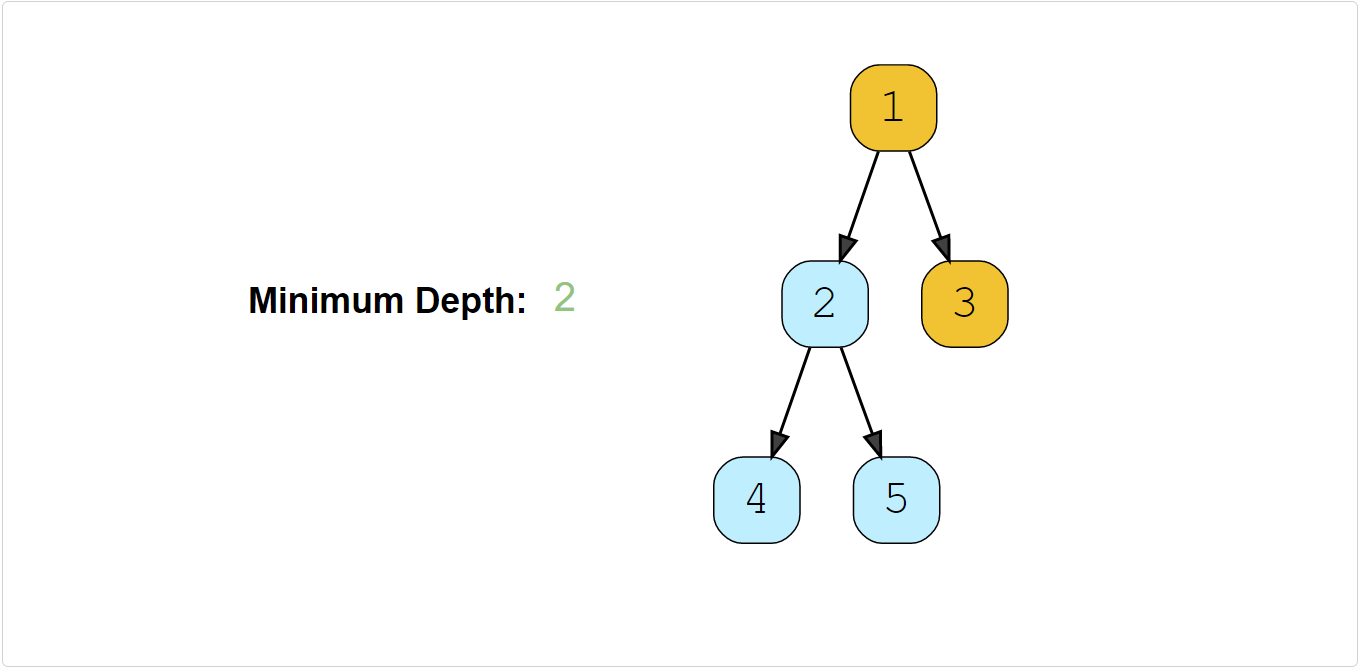
Example 2:

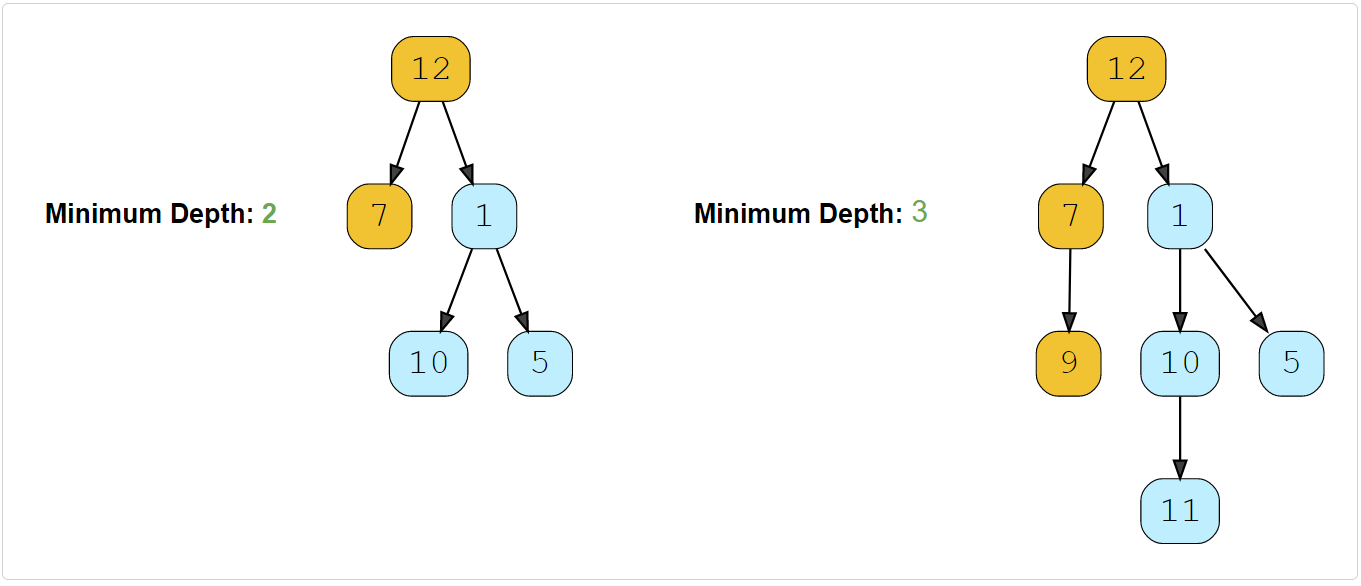
Constraints:

  • The number of nodes in the tree is in the range [0, 10^5].
  • -1000 <= Node.val <= 1000

Solution

This problem follows the Binary Tree Level Order Traversal pattern. We can follow the same BFS approach. The only difference will be, instead of keeping track of all the nodes in a level, we will only track the depth of the tree. As soon as we find our first leaf node, that level will represent the minimum depth of the tree.

Here is the visual representation of the algorithm:

Code

Here is what our algorithm will look like, only the highlighted lines have changed:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
from collections import deque


# class TreeNode:
#   def __init__(self, val):
#     self.val = val
#     self.left, self.right = None, None

class Solution:
    def findDepth(self, root):
        if root is None:
            return 0

        queue = deque()
        queue.append(root)
        minimumTreeDepth = 0
        while queue:
            minimumTreeDepth += 1
            levelSize = len(queue)
            for _ in range(levelSize):
                currentNode = queue.popleft()

                # check if this is a leaf node
                if not currentNode.left and not currentNode.right:
                    return minimumTreeDepth

                # insert the children of current node in the queue
                if currentNode.left:
                    queue.append(currentNode.left)
                if currentNode.right:
                    queue.append(currentNode.right)


def main():
    sol = Solution()
    root = TreeNode(12)
    root.left = TreeNode(7)
    root.right = TreeNode(1)
    root.right.left = TreeNode(10)
    root.right.right = TreeNode(5)
    print("Tree Minimum Depth: " + str(sol.findDepth(root)))
    root.left.left = TreeNode(9)
    root.right.left.left = TreeNode(11)
    print("Tree Minimum Depth: " + str(sol.findDepth(root)))


main()

Time complexity

The time complexity of the above algorithm is O(N), where ‘N’ is the total number of nodes in the tree. This is due to the fact that we traverse each node once.

Space complexity

The space complexity of the above algorithm will be O(N) which is required for the queue. Since we can have a maximum of N/2 nodes at any level (this could happen only at the lowest level), therefore we will need O(N) space to store them in the queue.

Similar Problems

Top Interview 150 | 104. Maximum Depth of Binary Tree Design Gurus Educative.io

Problem 1: Given a binary tree, find its maximum depth (or height).

Solution: We will follow a similar approach. Instead of returning as soon as we find a leaf node, we will keep traversing for all the levels, incrementing maximumDepth each time we complete a level. Here is what the code will look like:

Here is the visual representation of the algorithm:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
from collections import deque


# class TreeNode:
#   def __init__(self, val):
#     self.val = val
#     self.left, self.right = None, None


class Solution:
    def find_maximum_depth(self, root):
        if root is None:
            return 0

        queue = deque()
        queue.append(root)
        maximumTreeDepth = 0
        while queue:
            maximumTreeDepth += 1
            levelSize = len(queue)
            for _ in range(levelSize):
                currentNode = queue.popleft()

                # insert the children of current node in the queue
                if currentNode.left:
                    queue.append(currentNode.left)
                if currentNode.right:
                    queue.append(currentNode.right)

        return maximumTreeDepth


def main():
    sol = Solution()
    root = TreeNode(12)
    root.left = TreeNode(7)
    root.right = TreeNode(1)
    root.right.left = TreeNode(10)
    root.right.right = TreeNode(5)
    print("Tree Maximum Depth: " + str(sol.find_maximum_depth(root)))
    root.left.left = TreeNode(9)
    root.right.left.left = TreeNode(11)
    print("Tree Maximum Depth: " + str(sol.find_maximum_depth(root)))


main()

Level Order Successor (easy)

Design Gurus Educative.io

Problem Statement

Given a binary tree and a node, find the level order successor of the given node in the tree. The level order successor is the node that appears right after the given node in the level order traversal.

Example 1:

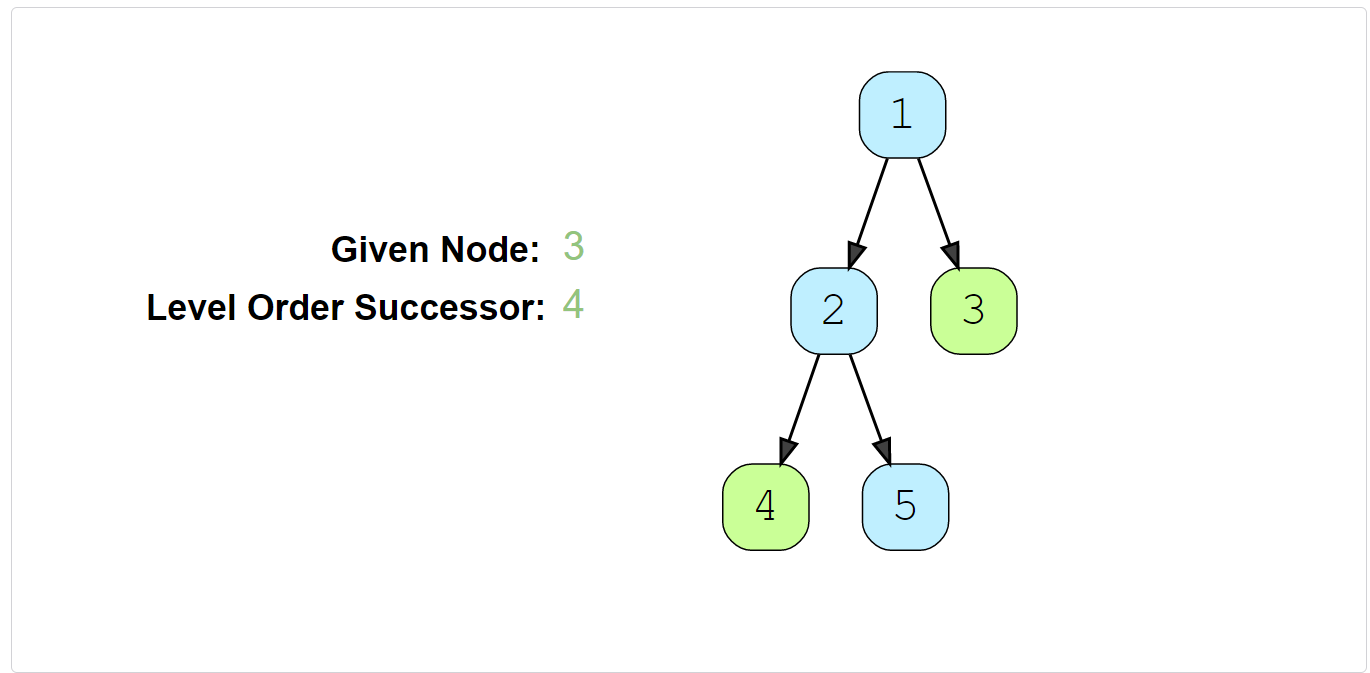
Example 2:

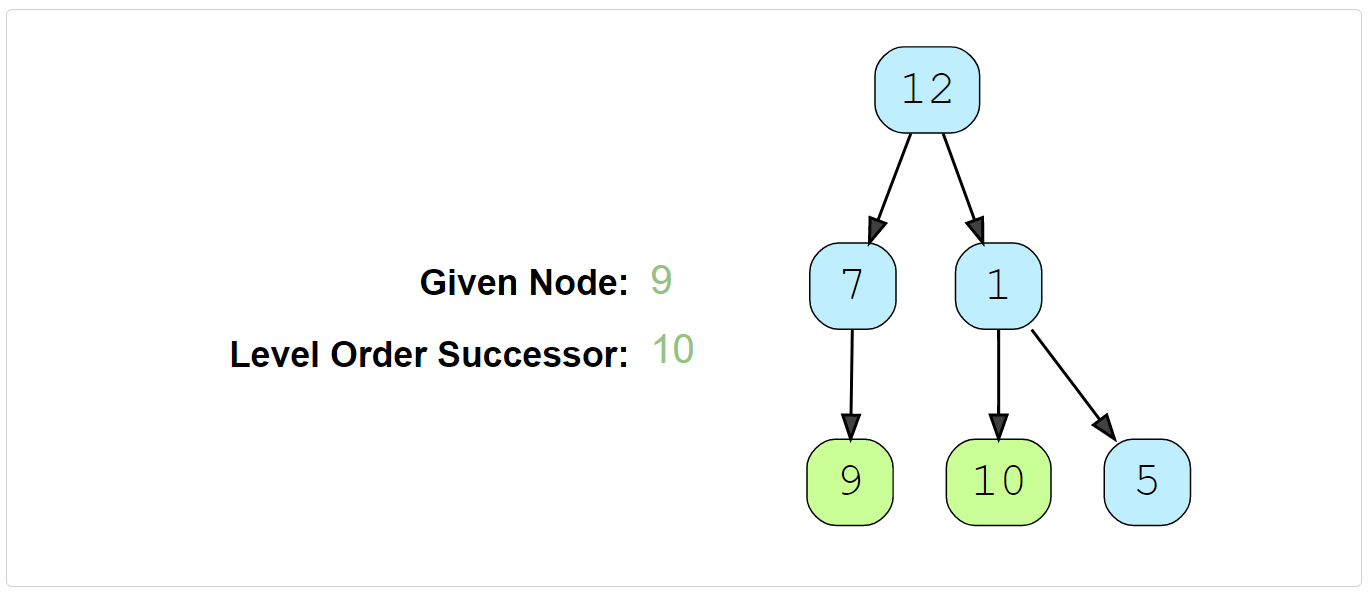
Example 3:

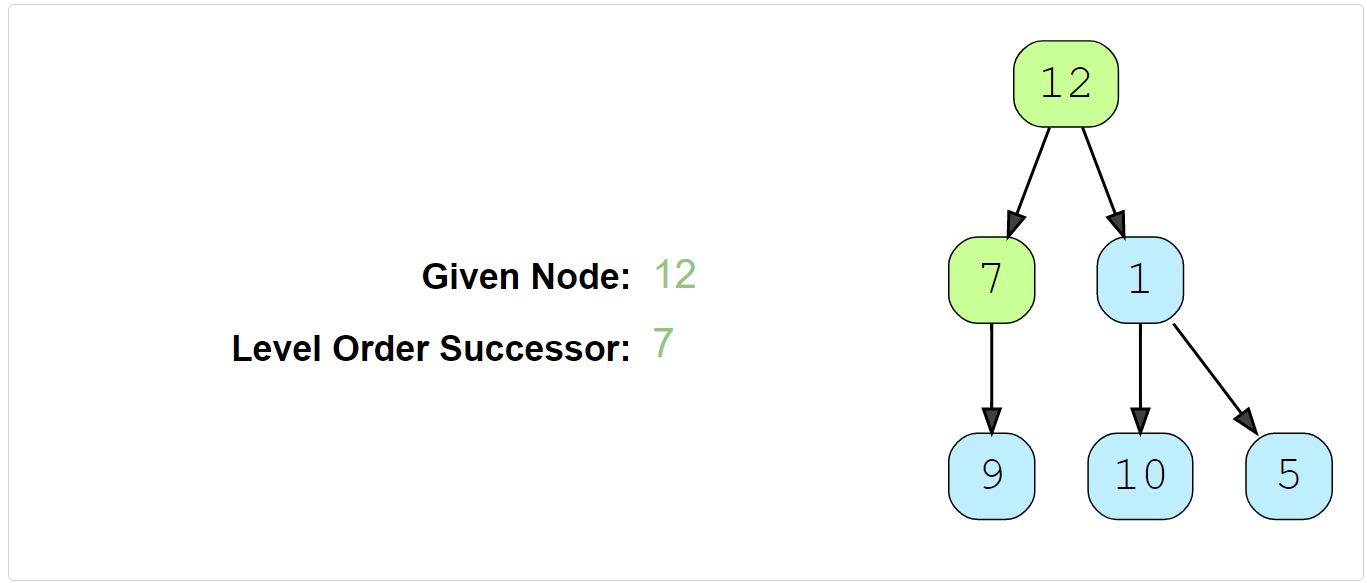
Constraints:

  • The number of nodes in the tree is in the range [0, 10^5].
  • -1000 <= Node.val <= 1000

Solution

This problem follows the Binary Tree Level Order Traversal pattern. We can follow the same BFS approach. The only difference will be that we will not keep track of all the levels. Instead we will keep inserting child nodes to the queue. As soon as we find the given node, we will return the next node from the queue as the level order successor.

Here is the visual representation of the algorithm:

Code

Here is what our algorithm will look like; most of the changes are in the highlighted lines:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
# 这是官方solution，但是这个方法有个局限就是所有的值都要唯一
from collections import deque


# class TreeNode:
#   def __init__(self, val):
#     self.val = val
#     self.left, self.right = None, None

class Solutiion:
    def findSuccessor(self, root, key):
        if root is None:
            return None

        queue = deque()
        queue.append(root)
        while queue:
            currentNode = queue.popleft()
            # insert the children of current node in the queue
            if currentNode.left:
                queue.append(currentNode.left)
            if currentNode.right:
                queue.append(currentNode.right)

            # break if we have found the key
            if currentNode.val == key:
                break

        return queue[0] if queue else None


def main():
    sol = Solutiion()
    root = TreeNode(1);
    root.left = TreeNode(2);
    root.right = TreeNode(3);
    root.left.left = TreeNode(4);
    root.left.right = TreeNode(5);

    result = sol.findSuccessor(root, 3)
    if result:
        print(result.val)

    root = TreeNode(12)
    root.left = TreeNode(7)
    root.right = TreeNode(1)
    root.left.left = TreeNode(9)
    root.right.left = TreeNode(10)
    root.right.right = TreeNode(5)

    result = sol.findSuccessor(root, 9)
    if result:
        print(result.val)

    result = sol.findSuccessor(root, 12)
    if result:
        print(result.val)


main()

Time complexity

The time complexity of the above algorithm is O(N), where ‘N’ is the total number of nodes in the tree. This is due to the fact that we traverse each node once.

Space complexity

The space complexity of the above algorithm will be O(N) which is required for the queue. Since we can have a maximum of N/2 nodes at any level (this could happen only at the lowest level), therefore we will need O(N) space to store them in the queue.

这里在遍历的时候就没有使用LevelSize这个变量,也就没有了While中还嵌套for这个循环，之前的题目中使用这个循环的意义是，由于之前的题目要求广度优先遍历的时候，输出要把一个层次中的放在一起，所以需要知道个数，再使用for循环遍历。如果题目要求没有这个，只要求输出广度优先遍历的结果，只要就不需要使用for循环，只要while(!queue.empty())有就够了。就像这个题目所写的一样。

Connect Level Order Siblings (medium)

116. Populating Next Right Pointers in Each Node Similar | Top Interview 150 |117. Populating Next Right Pointers in Each Node II Design Gurus Educative.io

Problem Statement

Given a binary tree, connect each node with its level order successor. The last node of each level should point to a null node.

Example 1:

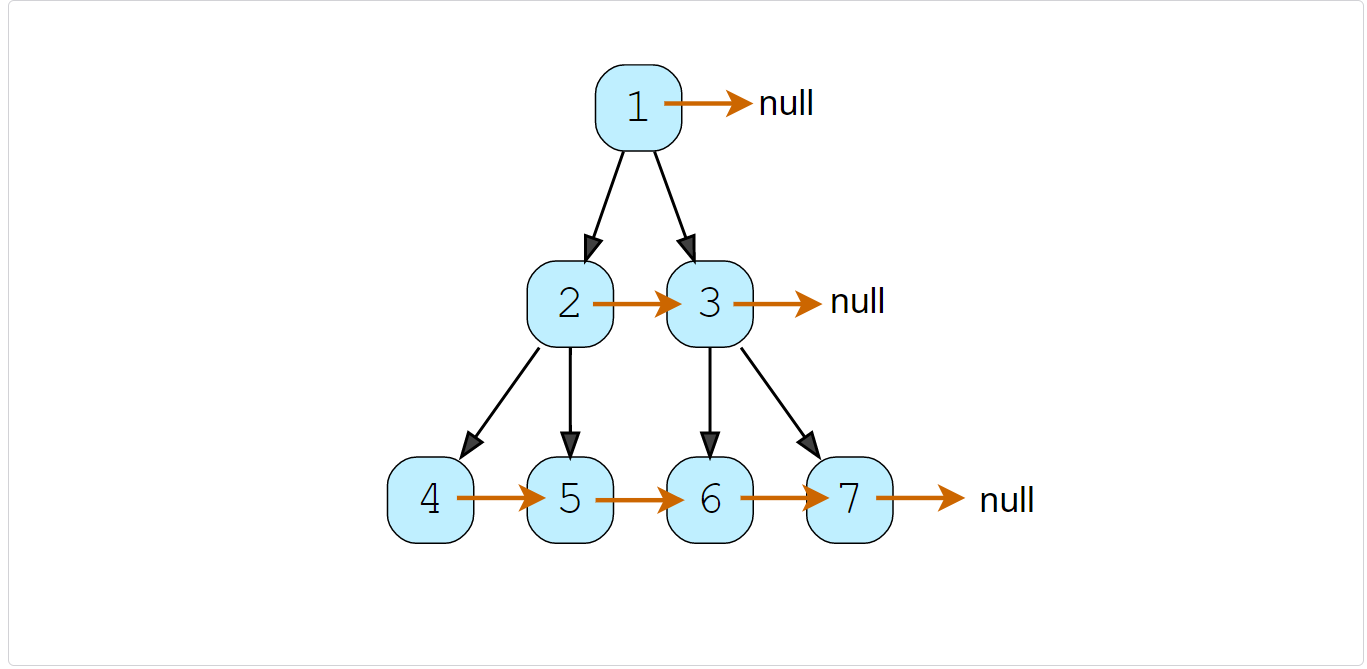
Example 2:

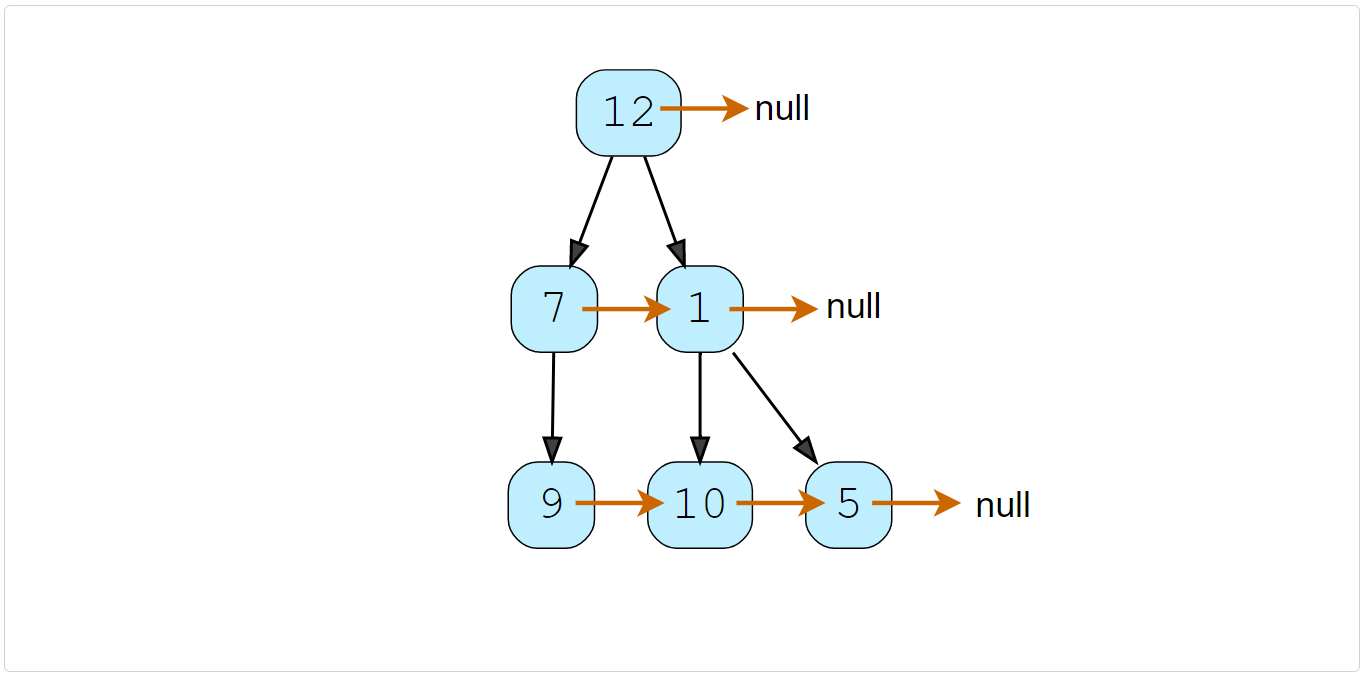
Constraints:

  • The number of nodes in the tree is in the range [0, 2^12 - 1].
  • -1000 <= Node.val <= 1000

Solution

This problem follows the Binary Tree Level Order Traversal pattern. We can follow the same BFS approach. The only difference is that while traversing a level we will remember the previous node to connect it with the current node.

Here is the visual representation of the algorithm:

Code

Here is the code for this algorithm:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
from collections import deque


# class TreeNode:
#   def __init__(self, val):
#     self.val = val
#     self.left, self.right, self.next = None, None, None

# level order traversal using 'next' pointer
def print_level_order(root):
    nextLevelRoot = root
    while nextLevelRoot:
        current = nextLevelRoot
        nextLevelRoot = None
        while current:
            print(str(current.val) + " ", end='')
            if not nextLevelRoot:
                if current.left:
                    nextLevelRoot = current.left
                elif current.right:
                    nextLevelRoot = current.right
            current = current.next
        print()


class Solution:
    def connect(self, root):
        if root is None:
            return

        queue = deque()
        queue.append(root)
        while queue:
            previousNode = None
            levelSize = len(queue)
            # connect all nodes of this level
            for _ in range(levelSize):
                currentNode = queue.popleft()
                if previousNode:
                    previousNode.next = currentNode
                previousNode = currentNode

                # insert the children of current node in the queue
                if currentNode.left:
                    queue.append(currentNode.left)
                if currentNode.right:
                    queue.append(currentNode.right)
        return root


def main():
    sol = Solution()
    root = TreeNode(12)
    root.left = TreeNode(7)
    root.right = TreeNode(1)
    root.left.left = TreeNode(9)
    root.right.left = TreeNode(10)
    root.right.right = TreeNode(5)
    root = sol.connect(root)

    print("Level order traversal using 'next' pointer: ")
    print_level_order(root)


main()

Time complexity

The time complexity of the above algorithm is O(N), where ‘N’ is the total number of nodes in the tree. This is due to the fact that we traverse each node once.

Space complexity

The space complexity of the above algorithm will be O(N), which is required for the queue. Since we can have a maximum of N/2 nodes at any level (this could happen only at the lowest level), therefore we will need O(N) space to store them in the queue.

Problem Challenge 1

Design Gurus Educative.io

Connect All Level Order Siblings (medium)

Given a binary tree, connect each node with its level order successor. The last node of each level should point to the first node of the next level.

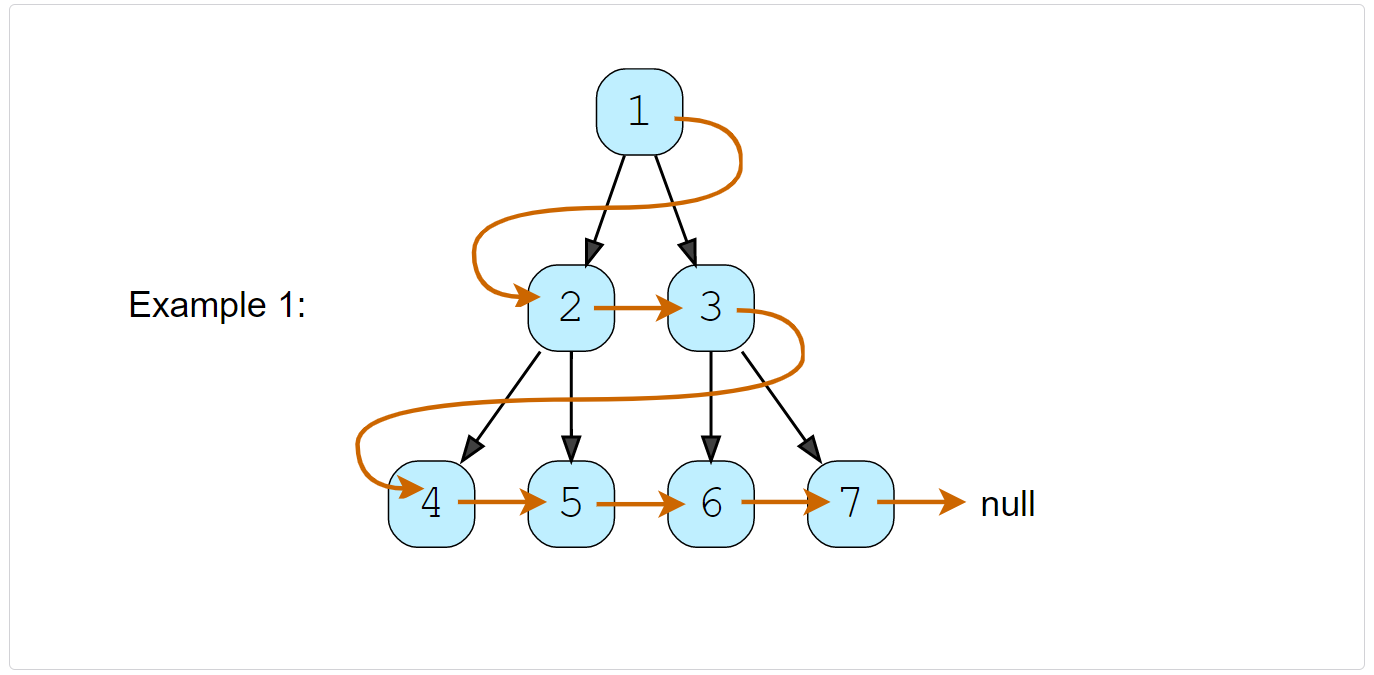
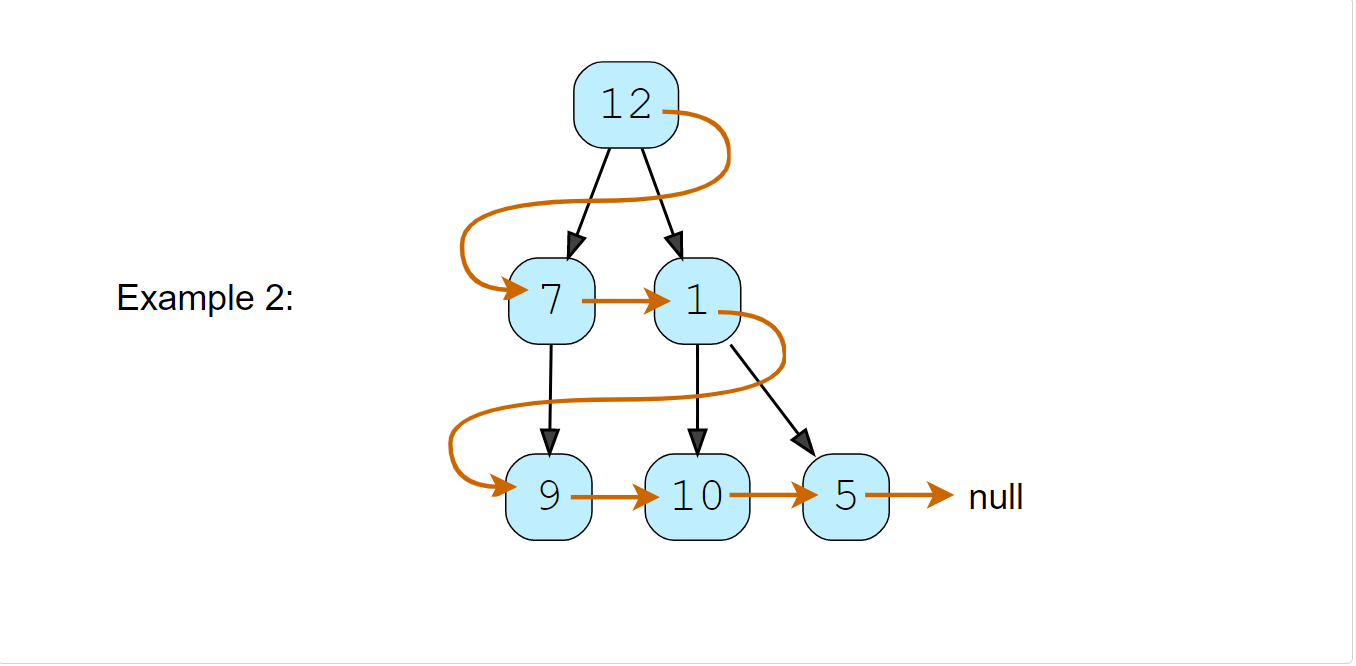
Solution

This problem follows the Binary Tree Level Order Traversal pattern. We can follow the same BFS approach. The only difference will be that while traversing we will remember (irrespective of the level) the previous node to connect it with the current node.

Code

Here is what our algorithm will look like; only the highlighted lines have changed:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
# 比较简单的还是，和上一题很类似
from collections import deque


# class TreeNode:
#   def __init__(self, val):
#     self.val = val
#     self.left, self.right, self.next = None, None, None

class Solution:
    def connect(self, root):
        if root is None:
            return root

        queue = deque()
        queue.append(root)
        currentNode, previousNode = None, None
        while queue:
            currentNode = queue.popleft()
            if previousNode:
                previousNode.next = currentNode
            previousNode = currentNode

            # insert the children of current node in the queue
            if currentNode.left:
                queue.append(currentNode.left)
            if currentNode.right:
                queue.append(currentNode.right)
        return root


# tree traversal using 'next' pointer
def print_tree(self):
    print("Traversal using 'next' pointer: ", end='')
    current = self
    while current:
        print(str(current.val) + " ", end='')
        current = current.next


def main():
    sol = Solution()
    root = TreeNode(12)
    root.left = TreeNode(7)
    root.right = TreeNode(1)
    root.left.left = TreeNode(9)
    root.right.left = TreeNode(10)
    root.right.right = TreeNode(5)
    sol.connect(root)
    print_tree(root)


main()

Time complexity

The time complexity of the above algorithm is O(N), where ‘N’ is the total number of nodes in the tree. This is due to the fact that we traverse each node once.

Space complexity

The space complexity of the above algorithm will be O(N) which is required for the queue. Since we can have a maximum of N/2 nodes at any level (this could happen only at the lowest level), therefore we will need O(N) space to store them in the queue.

Problem Challenge 2

Top Interview 150 | 199. Binary Tree Right Side View Design Gurus Educative.io

Right View of a Binary Tree (easy)

Given a binary tree, return an array containing nodes in its right view. The right view of a binary tree is the set of nodes visible when the tree is seen from the right side.

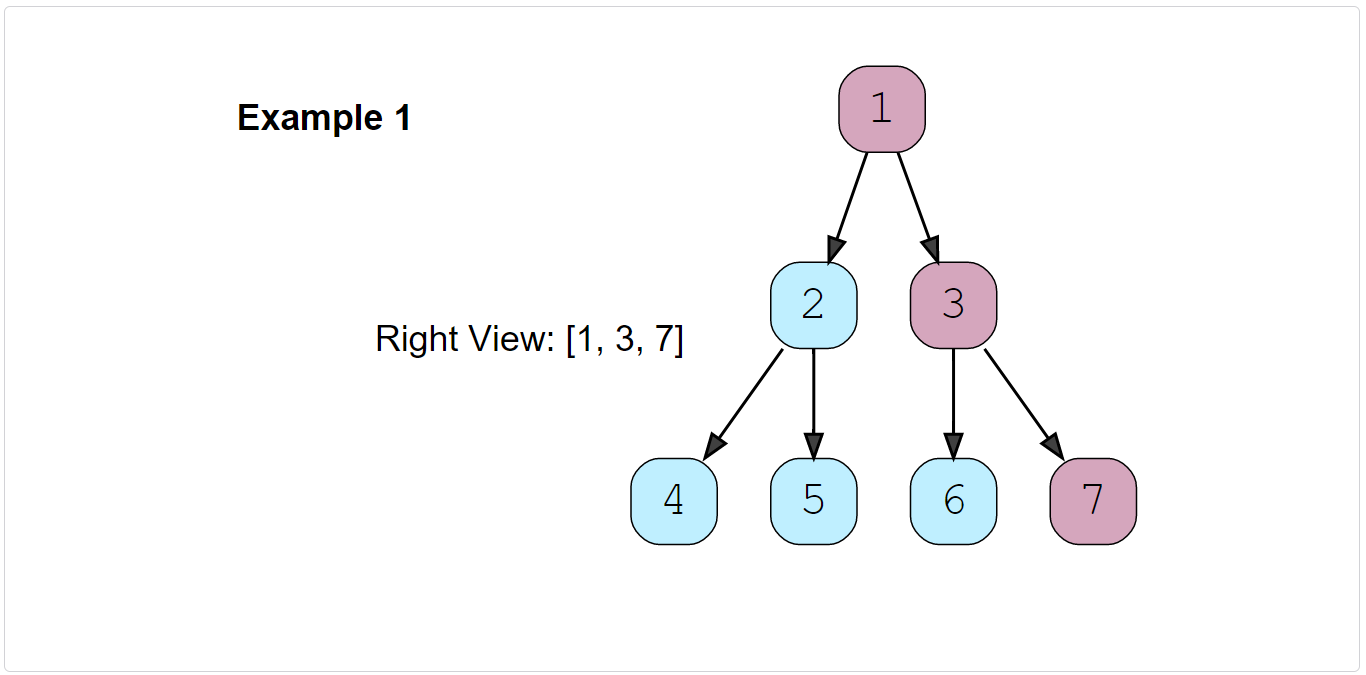
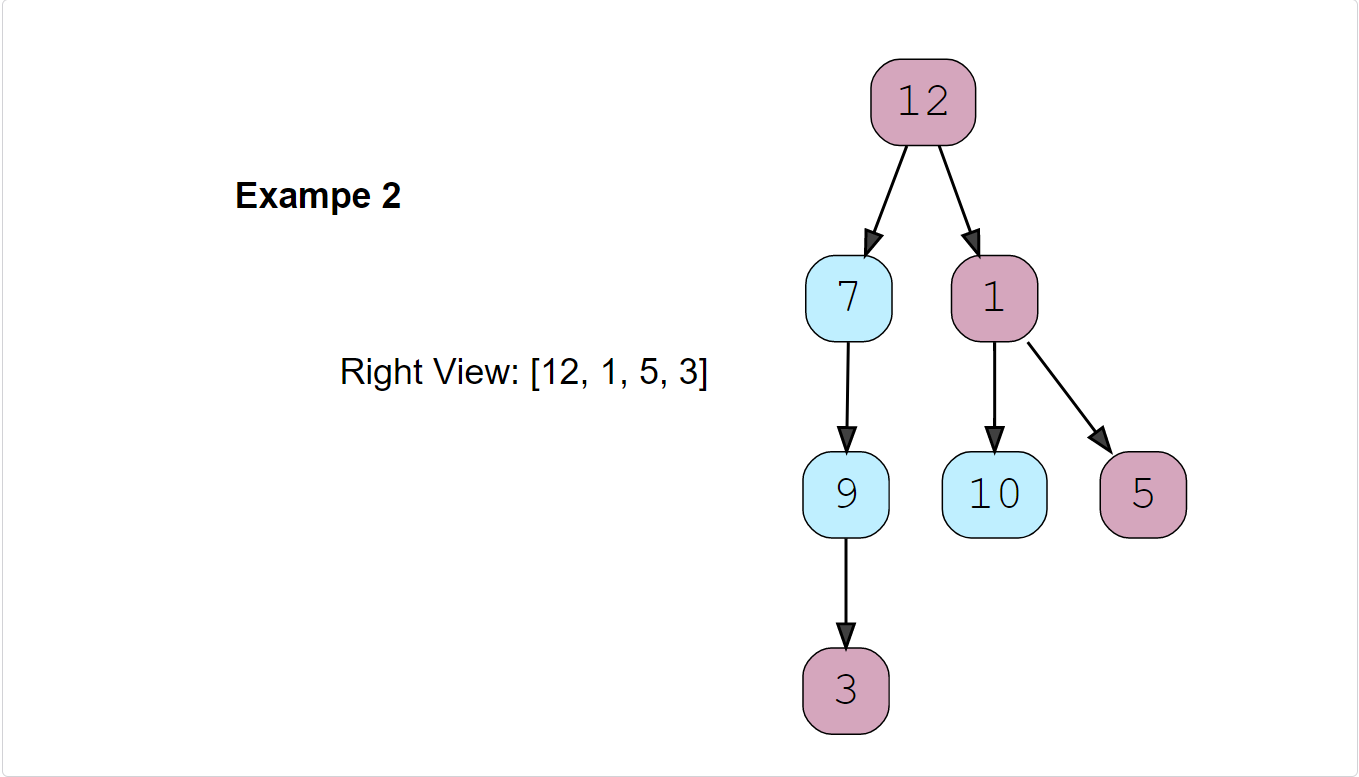
Constraints:

  • The number of nodes in the tree is in the range [0, 100].
  • -100 <= Node.val <= 100

Solution

This problem follows the Binary Tree Level Order Traversal pattern. We can follow the same BFS approach. The only additional thing we will be doing is to append the last node of each level to the result array.

Here is the visual representation of the algorithm:

Code

Here is what our algorithm will look like; only the highlighted lines have changed:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
from collections import deque


# class TreeNode:
#   def __init__(self, val):
#     self.val = val
#     self.left, self.right = None, None


class Solution:
  def traverse(self, root):
    result = []
    if root is None:
      return result

    queue = deque()
    queue.append(root)
    while queue:
      levelSize = len(queue)
      for i in range(0, levelSize):
        currentNode = queue.popleft()
        # if it is the last node of this level, add it to the result
        if i == levelSize - 1:
          result.append(currentNode.val)
        # insert the children of current node in the queue
        if currentNode.left:
          queue.append(currentNode.left)
        if currentNode.right:
          queue.append(currentNode.right)

    return result


def main():
  sol = Solution()
  root = TreeNode(12)
  root.left = TreeNode(7)
  root.right = TreeNode(1)
  root.left.left = TreeNode(9)
  root.right.left = TreeNode(10)
  root.right.right = TreeNode(5)
  root.left.left.left = TreeNode(3)
  result = sol.traverse(root)
  print("Tree right view: ")
  for val in result:
    print(str(val) + " ", end='')


main()

Time complexity

The time complexity of the above algorithm is O(N), where ‘N’ is the total number of nodes in the tree. This is due to the fact that we traverse each node once.

Space complexity

The space complexity of the above algorithm will be O(N) as we need to return a list containing the level order traversal. We will also need O(N) space for the queue. Since we can have a maximum of N/2 nodes at any level (this could happen only at the lowest level), therefore we will need O(N) space to store them in the queue.

Similar Questions

Problem 1: Given a binary tree, return an array containing nodes in its left view. The left view of a binary tree is the set of nodes visible when the tree is seen from the left side.

Solution: We will be following a similar approach, but instead of appending the last element of each level we will be appending the first element of each level to the output array.

Author：Hasuer

Link：https://hasuer.github.io/10-pattern-tree-breadth-first-search/index.html

Publish date：May 10th 2024, 5:24:15 pm

Update date：May 28th 2024, 11:28:19 am

License：本文采用知识共享署名-非商业性使用 4.0 国际许可协议进行许可

CATALOG
  1. 1. Introduction
  2. 2. Binary Tree Level Order Traversal (easy)
    1. 2.1. Problem Statement
    2. 2.2. Solution
    3. 2.3. Code
      1. 2.3.1. Time complexity
      2. 2.3.2. Space complexity
  3. 3. Reverse Level Order Traversal (easy)
    1. 3.1. Problem Statement
    2. 3.2. Solution
    3. 3.3. Code
      1. 3.3.1. Time complexity
      2. 3.3.2. Space complexity
  4. 4. Zigzag Traversal (medium)
    1. 4.1. Problem Statement
    2. 4.2. Solution
    3. 4.3. Code
      1. 4.3.1. Time complexity
      2. 4.3.2. Space complexity
  5. 5. Level Averages in a Binary Tree (easy)
    1. 5.1. Problem Statement
    2. 5.2. Solution
    3. 5.3. Code
      1. 5.3.1. Time complexity
      2. 5.3.2. Space complexity
    4. 5.4. Similar Problems
  6. 6. # Minimum Depth of a Binary Tree (easy)
    1. 6.1. Problem Statement
    2. 6.2. Solution
    3. 6.3. Code
      1. 6.3.1. Time complexity
      2. 6.3.2. Space complexity
    4. 6.4. Similar Problems
  7. 7. Level Order Successor (easy)
    1. 7.1. Problem Statement
    2. 7.2. Solution
    3. 7.3. Code
      1. 7.3.1. Time complexity
      2. 7.3.2. Space complexity
  8. 8. Connect Level Order Siblings (medium)
    1. 8.1. Problem Statement
    2. 8.2. Solution
    3. 8.3. Code
      1. 8.3.1. Time complexity
      2. 8.3.2. Space complexity
  9. 9. Problem Challenge 1
    1. 9.1. Connect All Level Order Siblings (medium)
    2. 9.2. Solution
    3. 9.3. Code
      1. 9.3.1. Time complexity
      2. 9.3.2. Space complexity
  10. 10. Problem Challenge 2
    1. 10.1. Right View of a Binary Tree (easy)
    2. 10.2. Solution
    3. 10.3. Code
      1. 10.3.1. Time complexity
      2. 10.3.2. Space complexity
    4. 10.4. Similar Questions
Total : 41
2024
2022
2021
Interview
技术笔记 Grokking-Interview-Pattern